Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Problems of dynamics of the particle

441

2.1 Tautochronous motions. Motions on a brachistochrone and on a

geodesic curve

In what follows, after presenting the problems of Abel and Puiseux, one considers –

in particular – the study of tautochronous motions. A particular attention is paid to the

motion on a brachistochrone curve or on a geodesic one, the study of which needs some

notions of variational calculus.

2.1.1 Abel’s problem

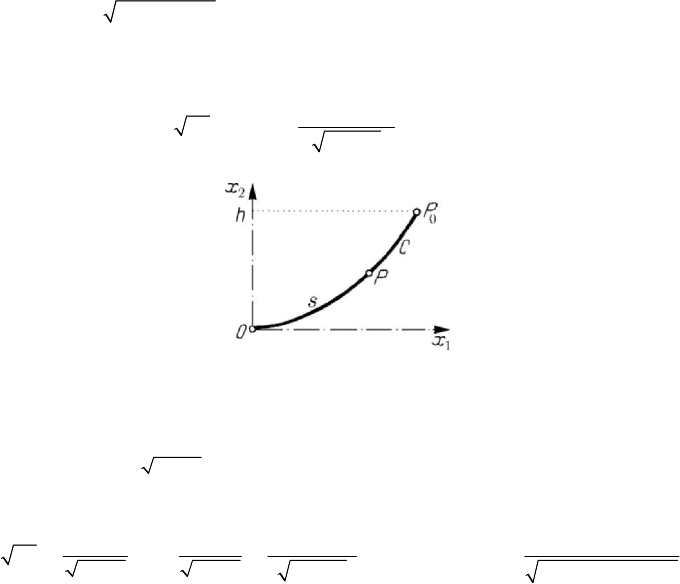
N.H. Abel tried to determine a curve

C , contained in a vertical plane and passing

through a given fixed point

O , so that a heavy particle P , which is moving without

friction on this curve, starting from the point

P , situated at an applicate h above the

point

O , reaches that point, without initial velocity, in an interval of time ()hττ= ,

[

]

0,ha∈ , assuming that the continuous function τ is given. We choose the

horizontal as

-axis, the

-axis being the local ascendent vertical (Fig.7.16); the

curve

C is specified by the equation

(

)

sxϕ

, (0) 0ϕ

[]

0,Caϕ ∈

, where s

is the curvilinear abscissa. The conservation theorem of mechanical energy gives

()

(d /d ) 2vstghx==−. Noting that ()st is a decreasing function, we may

write

()

222

d2 d()dsghxtxxϕ

′

=− − = ; by integration (

for 0t = and

0x = for t τ= ), we obtain an integral equation of the first kind, with a variable

superior limit

(

)

2()

′

−

∫

(7.2.1)

Figure 7.16. Abel’s problem.

To solve this integral equation, which is the first one appeared in mathematical

analysis, we use a particular ingenious procedure due to Abel; we multiply both

members by

d/huh− ,

[

]

0,ua

∈

and integrate with respect to

between the

limits

and u , so that

()

000 0

()d ( )d

2()d

()

uuh uu

hh x x

gxx

uh uh hx

uhhx

τϕ

′

−−−

−−

∫∫∫ ∫∫

MECHANICAL SYSTEMS, CLASSICAL MODELS

442

where the order of integration has been inverted (in fact, a double integral on a

triangular domain bounded by the lines

and hu

is calculated).

Noting that the latter integral is equal to

π , one obtains, finally,

()

ghh

−

∫

[

]

0,xa

∈

(7.2.1')

Following these ideas, Euler and Saladini deal with the determination of a curve

in a vertical plane, so that a heavy particle

P , which is moving without friction on this

curve, departing from the point

P , without initial velocity, reaches an arbitrary point

P in the same interval of time as that necessary if the particle would slide along the

bisecant

PP, finding thus a lemniscate. O. Bonnet showed that this lemniscate has

further the above mentioned property if we replace the gravitational field by a field of

central forces of attraction, proportional to the distance to the pole

P . As well, Fouret

considers a particle which is subjected to the action of a field of conservative forces in a

plane and which departs from the position

O without initial velocity; a problem to

determinate a family of homothetic curves

C passing through O , so that the particle

which departs from this pole describes an arc of curve

C till the point P in the same

interval of time in which the corresponding bisecant

OP would be travelled through is

put. The problem has a solution if the potential function is of the form

(, ) ( / ()) ()Ur rθψϕθϕθ= in polar co-ordinates, ϕ and ψ being arbitrary functions

of class

C ; the equation of the curve

is, in this case, of the form

()

()erk

ϕθ

−

′

∫

, constk

(7.2.2)

Analogously, one may put the problem to determine the field of conservative forces

which act upon a particle the trajectory of which is a curve from the family of curves

previously considered; if the equation of the curve

is of the form ()rkωθ= ,

constk =

, then the potential function is of the above mentioned form, where

[]

()/ () 1d

() ()e

ωθ ωθ θ

ϕθ ωθ

′

−+

∫

(7.2.2')

2.1.2 Puiseux’s problem

In connection with tautochronous motions we consider – first of all – a particular

problem, put and solved by Puiseux. It is thus asked to determine a law of force

()FFx= for which a rectilinear and frictionless motion is tautochronous with respect

to the pole

of the trajectory (Fig.7.17). The conservation theorem of mechanical

energy leads to

[

]

2() ()mx x xψψ=−

where we denoted by

() ()d

xFψξξ=−

∫

, (0) 0ψ

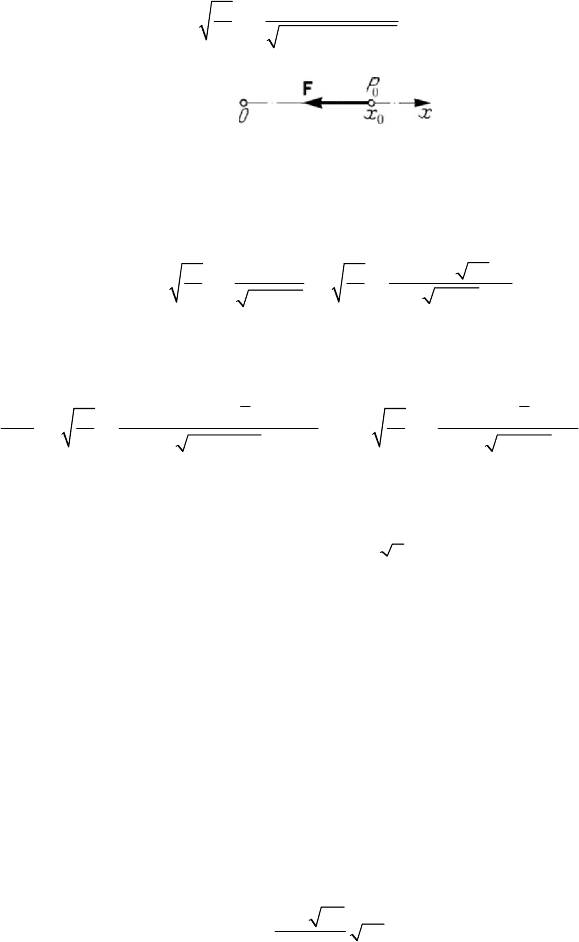
Problems of dynamics of the particle

443

an increasing positive function, because

()Fx is a function obviously negative for

0x > , if we assume that

0x > (the force must be directed towards the pole O ,

because the particle must move towards that point). The particle reaches the point

O in

an interval of time equal to

() ()

ψψ

−

∫

(7.2.3)

Figure 7.17. Puiseux’s problem.

If we denote

()xzψ = ,

()xzψ

zzu

and ()xzχ

, where χ is the inverse

function, it results

()d ( ) d

zz zu zu

χχ

′

−

∫∫

;

the condition that

τ be not dependent on

x , hence on

z , is put in the form

00 0

000 00

() () () ()

dd0

d2 2

zuzu zu z z z

zzzu zzz

χχ χχ

′′ ′ ′′ ′

===

−−

∫∫

for any

z , so that we must have 2() ()0zz zχχ

′

′′

= (otherwise we may choose a

z sufficiently small so that the integrand be of a constant sign, so that the condition

would no more be fulfilled). We get

() 2zczχ

constc

, an additive constant

being equal to zero, because

z and ()xzχ

vanish simultaneously; it results

() /4zxxcψ==

, so that

() /2Fxxcψ

′

=− =−

. We see thus that the only force

()FFx= which leads to a tautochronous rectilinear motion is a force in direct

proportion to the distance (which will be studied in Chap. 8, Subsec. 2.2.1).

If the resultant of the given forces depends on the position as well as on the velocity,

the problem is more intricate. Lagrange gave a law for the force for which the

tautochronism takes place and from which – if the velocity is no more involved – one

obtains the previous results. But this law does not contain all possible cases; e.g.,

Brioschi gave a more general formula.

2.1.3 Tautochronous motions

If we make

() consthττ== in the formula (7.2.1'), then we obtain

()

sx x

(7.2.4)

MECHANICAL SYSTEMS, CLASSICAL MODELS

444

denoting

/gaτπ= , we find again the equation of the cycloid (Fig.7.12), considered

in Subsec. 1.3.5. We have seen that the cycloid is a tautochronous curve, the respective

motion being a tautochronous one with respect to the point of tautochronism

O , which

is reached by the particle, acted upon by its own weight, in the same interval of time

τ , independent of the initial position, if the initial velocity vanishes. Besides, the

cycloid is the only tautochronous curve with respect to a gravitational field.

In general, we say that a motion (hence, a curve

C ) is tautochronous if there exists a

point

′

(called point of tautochronism) on this curve, so that a particle which is acted

upon by given forces of resultant

F and which, departing from the position

P ,

frictionless and without initial velocity, reaches the position

′

in an interval of time

independent of

P . Projecting the equation of motion on the tangent to the curve, we

may write

()

mFF fs

== =

(7.2.5)

where the second member is function only on the curvilinear co-ordinate

s , if we

assume that the resultant of the given forces depends only on the position (

()=FFr).

The equation (7.2.5) is identical with the equation of the rectilinear motion on the

Os -

axis, if the particle is subjected to the action of a tangential force

F .

Taking into account the results obtained in the preceding subsection, we must have

()

sks=− , so that the trajectory C be tautochronous, that one being a necessary

and sufficient condition; the point of tautochronism

is – obviously – a stable

position of equilibrium. The solution of the problem is indeterminate, to determine it

being necessary a supplementary condition. For instance, one may put the condition that

the curve

C lays on a given fixed surface

(

)

123

,, 0xxx

F , adding the obvious

relation

dd d

xx s= ; one may obtain thus the parametric equations of the trajectory

()

xxs= ,

1, 2, 3i =

, introducing two new constants of integration besides

. In the

case of a conservative force, we obtain easily

()

123

Ux x x s K

−+, constK

(7.2.6)

As well, we may put other conditions, e.g., that the curve

C be tautochronous, with the

same point of tautochronism for other given forces of resultant

′

F ; we introduce thus a

new condition of the form

Fks

′′

=−

, constk

′

(7.2.5')

Hence, the curve obtained is tautochronous for a force

λλ

′

FF, λ , λ

′

constant

positive scalars. If the second force is conservative too, of potential

Problems of dynamics of the particle

445

()

123

Uxxx s K

′

′′

=− +

, constK

′

(7.2.6')

the tautochronous curve will stay on the surface

()

[]

()

[]

123 123

,, ,,kUxxx K kUxxx K

′

′′

−= −

(7.2.7)

In the general case of a resistent medium of resistance

()Rv

 , the resultant of

the given forces depending also on the velocity (

(, )

FFrv), the equation of motion

reads

(

)

 ;

(7.2.5'')

we come thus back to the previous case of rectilinear motion for which a necessary and

sufficient condition of tautochronism is not known, being possible to use – in particular

– the law of force given by Lagrange.

2.1.4 Considerations on variational calculus

To study the motion on a brachistochrone, there are necessary some results

concerning variational calculus. Let thus be an integral of the form

() (;, )d

Iy Fxyy x

′

≡

∫

(7.2.8)

where

(;, )Fxyy

′

is a known real function of arguments

,xy

and d/dyyx

′

≡ , of

class

with respect to these arguments; the value of this integral depends on how is

chosen the function

()yyx= , wherefrom the notation used, as well as the

denomination of functional. We assume that the admissible arguments

()yx are of

class

C and that, at the extremities of the interval

[

]

,xx , they take the given values

,yy; in this case, the set

{

}

()yx of the admissible arguments ()yx may be seen as a

family of smooth curves, passing through the points

(,)xy and

(,)xy of which we

must choose one, which minimizes the functional

()Iy. A necessary condition to

determine this curve is the Euler-Poisson equation

′

−

= ,

(7.2.8')

associated to the variational problem

() minIy

, where

F and

′

, represent the

partial derivatives with respect to the corresponding arguments; developing, one obtains

yy yy yx

FFFF

′′ ′ ′

+−=.

(7.2.8'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

446

If the condition (7.2.8') or (7.2.8'') holds, we say that the functional is stationary on the

curve

()yx . Because this condition is only necessary, one must then verify if the

solution of the respective differential equation minimizes effectively the functional

()Iy.

Let be now a functional of the form

12 12 1 2

() ( , ;, , )d d

Iu Fx x uu u x x≡

∫∫

(7.2.9)

on a set

{

}

(, )ux x of functions of class

C , which take continuously given values on

the frontier of the domain

D ; F is a given function of class

C in the arguments

,,xxu,

/uux≡∂ ∂ ,

/uux

≡

∂∂ on the domain of definition of those

arguments. The Euler-Ostrogradskiĭ equation corresponding to the problem of

minimum reads

(

)

(

)

,1 ,2

uu u

FF F−− =

(7.2.9')

being a necessary condition too. In particular, in the case of the functional

12 12 12

() 2( , ) d d

Iu u u fx x u x x≡++

⎡⎤

⎣⎦

∫∫

(7.2.10)

we find an effective minimum given by Poisson’s equation

12 12

(, ) (, )ux x fx xΔ=

(7.2.10')

on the domain

D .

Analogously, the functional

1 2 1 2 11 12 22 1 2

() ( , ;, , , , , )d d

Iu Fx x uu u u u u x x≡

∫∫

(7.2.11)

leads to the Euler-Ostrogradskiĭ equation

(

)

(

)

(

)

(

)

(

)

1 2 11 12 22

,1 ,2 ,11 ,12 ,22

uu u u u u

FF F F F F−−+ + + =

(7.2.11')

As well, for the functional

123 12 3 1 2 3

() ( , , ;, , , )d d d

Iu Fx x x uu u u x x x≡

∫∫∫

(7.2.12)

defined on a three-dimensional domain, we obtain the Euler-Ostrogradskiĭ equation

(

)

(

)

(

)

12 3

,1 ,2 ,3

uu u u

FF F F−−− =

(7.2.12')

In the case of several functions

()

yx, 1,2,...,kn

, of the same independent

variable

x , the functional

Problems of dynamics of the particle

447

12 12 12

( , ,..., ) ( ; , ,..., , , ,..., )d

nnn

Iyyy Fxyyyyyyx

′′ ′

≡

∫

(7.2.13)

leads to the Euler-Lagrange system of equations

()

′

−=

, 1,2,...,kn

(7.2.13')

which represent necessary conditions of stationarity.

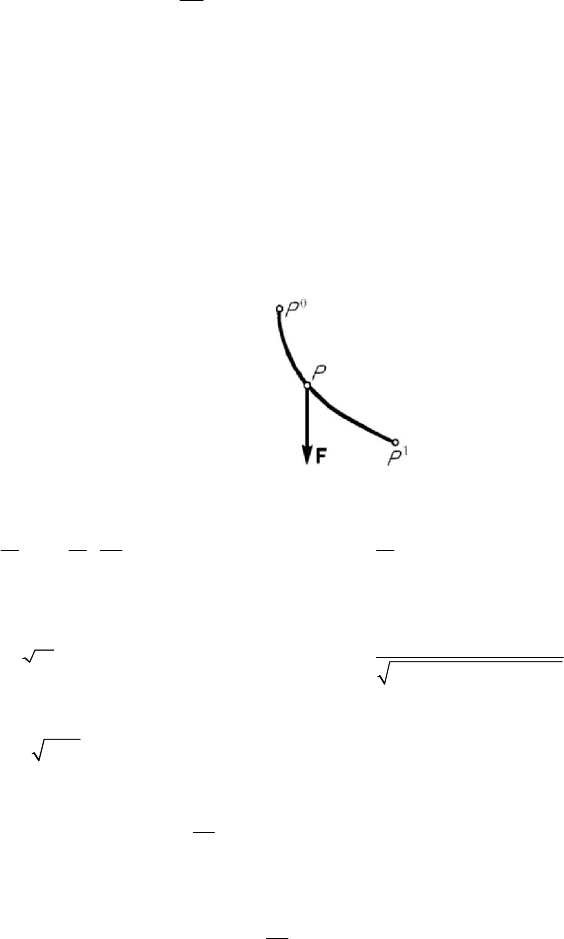
2.1.5 Motion on a brachistochrone

The problem to determine a curve

C passing through the points

P and

P is put,

so that a particle

P , which departs from

P with an initial velocity

v and is subjected

to the action of a field of conservative forces

gradFU

, does slide frictionless along

the curve from

in a minimal interval of time (Fig.7.18); a curve C which has

this property is a brachistochrone curve for the field of given forces. The conservation

theorem of mechanical energy leads to

Figure 7.18. Motion of a particle on a brachistochrone.

(

)

123

(, , )

22d

mms

vUxxxh

== +

2 000

123

(,, )

h v Uxxx=−

(7.2.14)

wherefrom

123

(,, )d

tm xxxsϕ=

∫

[]

123

(,, )

2(,,)

xxx

Ux x x h

ϕ =

;

(7.2.14')

noting that

()sϕϕ= , by the agency of the functions ()

xxs

, 1, 2, 3i

, and that

sxxs

′

, d/d

xxs

′

= , we may write the Euler-Lagrange stationarity condition

(7.2.13') in the form

()

ϕϕ

′

−=

, 1, 2, 3i

(7.2.15)

Vectorially, we have

grad ( )

ϕϕ

−

= 0τ ,

(7.2.15')

MECHANICAL SYSTEMS, CLASSICAL MODELS

448

where

d/ds= rτ is the unit vector of the tangent to the curve. It results

grad

ϕϕ

−

−=0τν,

(7.2.15'')

where we took into account the first Frenet formula,

1/ρ being the curvature of the

curve, while ν is the principal normal; a scalar multiplication by

leads to the identity

grad d / d d / d 0ssϕϕ⋅− =r , so that the equations (7.2.15)-(7.2.15'') are reduced to

only two equations.

We notice that the equation (7.2.15') is of the same form as the equation of

equilibrium (4.2.57) of a perfectly flexible, torsionable and inextensible thread, where

ϕ=T τ , T ϕ= being the tension in the thread, while () grads ϕ

−p is the external

conservative load on the unit length, which acts upon the thread, corresponding to the

formula (4.2.58'); as well, the equations (7.2.15) may be put in correspondence with the

equations (4.2.59). Taking into account (7.2.14'), it results

,,ii

Uϕϕ=− , 1, 2, 3i = , so

that

( ) grad gradsUϕϕ ϕ=− = =pF, where F is the given force which acts

upon the particle in motion on a brachistochrone. Projecting on the principal normal to

the curve

, one obtains

//pFT

νν

ϕρϕρ==−=−, wherefrom

1/F

ϕρ=− ,

relation which gives the curvature of the brachistochrone as a function of the given

force which acts upon the particle. From (7.2.14), one may write

1/mv ϕ=

; on the

other hand, the equation of motion in intrinsic co-ordinates reads

/mv F R

νν

ρ =+,

where

R is the constraint force which acts upon the particle constrained to stay on the

curve

C , which must be determined. There results

1/FR

νν

ρϕ+= , so that

2/N

ρϕ= and

2NF

νν

− ; (7.2.16)

we may state

Theorem 7.2.1 (Euler). In the motion on a brachistochrone, the modulus of the normal

constraint force is twice greater than the modulus of the normal component of the

resultant of the given forces.

constT ϕ== along the thread, we may suppose that one stays on a smooth

surface

constϕ

(equipotential surface), ()sp being a constraint force ()sR ; in this

case, the unit vector ν coincides with the unit vector

n of the normal to the surface

and the brachistochrone is a geodesic curve of the surface. Noting that, in this case,

() ()ssϕ=RF

, it results that such a situation is obtained only if the field of given

forces is normal to the searched brachistochrone at each point of it. From this point of

view, we may search such curves, situated on a surface and corresponding to a field of

given conservative forces. The equation (7.2.15') reads

grad grad ( )

ϕλ ϕ

−=0τ ,

(7.2.17)

Problems of dynamics of the particle

449

where

123

(, , ) 0

xxx = is the equation of the surface; to this equation there

corresponds the equation (4.2.70) of the threads, and the study can be made

analogously.

Taking

=v0 and choosing

Umgx

, where

Ox is along the local descendent

vertical, we get

0h = , so that

1/ 2mgxϕ = ; the equations (7.2.15) lead to

,constCC

wherefrom

12 21

constCx Cx=+, the trajectory being in a vertical plane. Taking this

plane as

0x = (hence

), it results (

for

and

1/ 2Ca= )

−

;

we denote

(1 cos )xa θ=− and get, by integration,

(sin)xaθθ

− , so that, in

case of a gravitational field, the brachistochrone is a cycloid, the concavity of which is

opposite to the direction of these forces. Euler’s theorem has been verified in Subsec.

1.3.5 for this particular case.

2.1.6 Motion on a geodesic curve

The motion of a particle on a geodesic curve of a smooth fixed surface

has been

emphasized in Chap. 6, Subsec. 2.2.2. To have such a trajectory, it is necessary and

sufficient that

F =

, hence that the force

be in the osculating plane of the

trajectory; on the other hand, the motion is uniform only if

, hence if the given

force is normal to the surface

S and has an influence only upon the constraint force

R . Noting that along a geodesic line we have

, the normal n to the surface

123

(, , ) 0

xxx = being collinear with grad

, we may write the equations of the

geodesic lines in the form

grad

λ=

, 1, 2, 3i

(7.2.18)

where

λ is an arbitrary scalar and where we took into account the first Frenet formula

given by

d/dsρ= rν

. If the motion of the particle is uniform, then

ddsvt= , and

the equations of motion along the geodesic curves are of the form

grad

λ=



r ,

,ii

xfλ=

1, 2, 3i

vλλ=

(7.2.18')

P and

P are two points on a geodesic line, then the distance l between these two

points is

ls xxs

′

∫∫

′

;

(7.2.19)

MECHANICAL SYSTEMS, CLASSICAL MODELS

450

we put the problem to determine the functions

()

xxs

so that the functional l be

stationary (in fact, minimal). Because these functions are linked by the relation

123

(, , ) 0

xxx = , we use the method of Lagrange’s multiplier, searching functions for

which the functional

()

xx f sλ

′′

∫

is stationary,

λ being an indeterminate parameter; the stationarity conditions (7.2.13')

give

d/d 0

′

−=

1, 2, 3i

, thus finding again the equations (7.2.18), which

coincide with the equations (7.2.17) for

1ϕ

. It results that the shortest way on a

surface between two points of it is along the geodesic line which joints them and is

unique. This property is characteristic for the geodesic lines, which are “the most

straight lines” on the surface. In particular, if there are straight lines which stay on a

surface (e.g., the case of a ruled surface), these ones are – obviously – geodesic lines; a

particle which is acted upon by not one force and is launched along such a straight line

travels through it corresponding to the principle of inertia, the constraint force

vanishing.

If the surface is given by the parametric equations

(, )

xxqq

, 1, 2, 3i = , then

the distance is written in the form

lgqqs

αβ β

′′

∫

′

αβ βα

== ,

(7.2.19')

where the Greek dummy indices correspond to the summation with respect to 1 and 2.

The Euler -Lagrange equations lead to

()

gq qq

αβ

βγ β β

∂

′′′

−

∂

, 1, 2γ

;

differentiating and noting that

qq qq

qqq

βγ αγ βγ

αα

ββ

αα

∂∂

∂

⎛⎞

′

′′′

⎜⎟

∂∂∂

⎝⎠

we get the equations

[

]

,0gq qq

βγ β β δ

βδ γ

′′ ′ ′

, 1, 2γ

(7.2.19'')

where we have introduced Christoffel’s symbol of the first kind. Multiplying by the

normalized algebraic complement

αγ

, summing and using Christoffel’s symbol of

second kind, there result the equations of the geodesic lines in the normal form

qqq

αγ

βγ

⎧⎫

′′ ′ ′

⎨⎬

⎩⎭

, 1, 2γ

;

(7.2.19''')