Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Problems of dynamics of the particle

431

sin

θωθ μ

−

=−



vanishes at the moment

/t πμ

(Fig.7.11); then the motion follows the same law,

the particle returning till the point

P at a time

2/t πμ

a.s.o. The oscillations are

isochronic, the period

2/ 2/T πμ π ω λ== − (greater than that of the motion in

vacuum) not depending on the amplitudes

123

...θθθθ>>>>; we notice also

that

12132

/ / / ... e

πλ μ

θθ θθ θθ

−

====,

so that the absolute values of the amplitudes form a geometric series of ratio

πλ μ−

Hence, the motion is damped in an infinite time, the particle reaching the lowest

position (stable position of equilibrium).

Figure 7.11. Simple pendulum in a resistent medium.

If, in the case of oscillations of finite amplitude, we consider a resistance

proportional to the square of the velocity (aerodynamic damping), then

Rmlkθ=



and the equation (7.1.50) becomes

22 2

sin 0kθθωθ++ =

 

(7.1.53)

for an ascendent motion; in the case of a descendent motion, we replace

k by

k− .

Noting that

(

)

d/d d /2dθθθθ θ θ==

   

, we may write the equation (7.1.53) in the

form

(

)

22 2

sin

θωθ

±=−



(7.1.53')

the general integral of which is given by

()

22 2

ecos2sin

θθθ

∓



∓

(7.1.53'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

432

where

C is a constant which must be determined; the relation (7.1.53'') represents, in

fact, an equation with separate variables, and the quadrature may be calculated for small

amplitudes.

1.3.4 Elliptic pendulum

Let

P be a heavy particle constrained to move on an ellipse of semiaxes a and b of

equation

= ,

(7.1.54)

situated in a vertical plane, the

Ox -axis being the descendent vertical. Using the

parametric representation

cosxaq= ,

sinxbq

, 02q π

≤

< ,

the theorem of kinetic energy

(

)

12 1

d/2mx x mgx+=

⎡⎤

⎣⎦

 leads to

(

)

(

)

22 2 2 2 2 2

sin cos sin cos sinaqbqqabqqqagq++− =−  .

(7.1.55)

In the case of small motions around the point

(,0)Pa , which is a stable position of

equilibrium, we have

sinqq

≅

cos 1q

≅

 , so that the equation (7.1.55)

becomes

0qqω+= ,

ω = ;

(7.1.55')

it results

(

)

cosqq ttω

− , the motion being periodic, isochronic, of period

2 b

= .

(7.1.55'')

abl==, then one obtains the results in Subsec. 1.3.1, for instance Galileo’s

formula (7.1.45'').

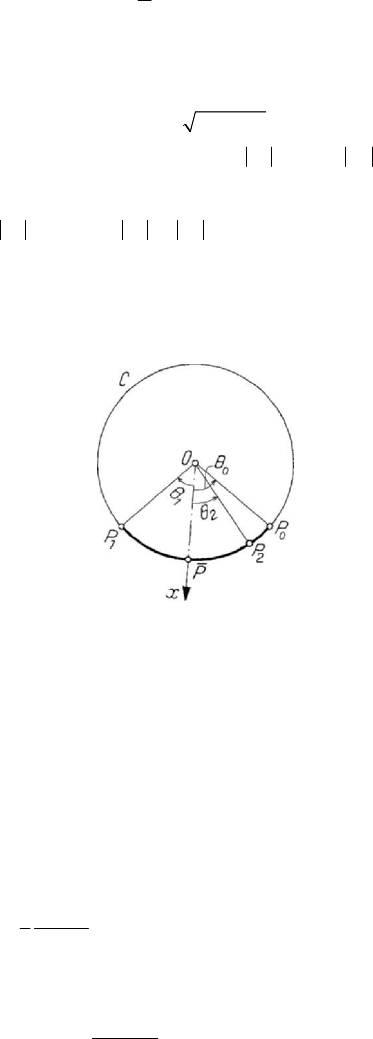
1.3.5 Cycloidal pendulum

Let us consider the motion of a heavy particle

P on a cycloid C with a horizontal

basis, situated in a vertical plane and having the concavity towards the positive

direction of the

Ox -axis. The axis

Ox is tangent to the cycloid as its lowest point,

while the

Ox -axis (an ascendent one) is the symmetry axis of the cycloid (Fig.7.12).

Starting from the definition of the cycloid as a locus (see Chap. 5, Subsec. 1.3.4), we

obtain its parametric equations in the form

(sin)xaθθ=+ ,

(1 cos )xa θ

− ,

[

]

,θππ

∈

− ,

Problems of dynamics of the particle

433

where

2xa

is the straight line on which the generating circle C (of centre O

′

and

radius

a ) of the cycloid is rolling without sliding. Departing from

222

dddsxx=+,

we find

d2cos(/2)d 2/dsa axxθθ==; by integration, we obtain

22sax=

4sin(/2)a θ= , so that

d/d /4xssa

. Euler’s equations of motion are written in

the form

mv ms F mg

===−





+ ,

Figure 7.12. Cycloidal pendulum.

wherefrom it results

0ssω+= ,

ω = ;

(7.1.56)

hence,

cosss tω

, (7.1.56')

assuming that the particle is launched without initial velocity from the point

P , of

curvilinear co-ordinate

s , at the initial moment

t . The period of the motion is

ππ

== = ;

(7.1.56'')

this period does not depend on the amplitude

s , so that the oscillations are isochronic

(independent of their magnitude). On the other hand, a particle in a free fall from the

MECHANICAL SYSTEMS, CLASSICAL MODELS

434

point

P reaches the point O (the lowest point of the cycloid) in the time /4T , which

is independent of

s , hence of the initial position; this is the property of tautochronism

of the cycloid. We say that the motion is tautochronous, independent of the magnitude

of the oscillations, the cycloid being thus a tautochronous curve. This property has been

put in evidence by Huygens, which realized a cycloidal pendulum with the aid of the

evolute of a cycloid, that one being a cycloid too. The thread by which is connected the

particle

P (unilateral constraint) is fixed at the point

(cuspidal point of a cycloid

concretely built up); but the resistances which intervene modify considerable the

motion.

Taking into account the theorem of the kinetic energy, we may write

(

)

2vgxx=−, where the ordinate

x corresponds to the initial position

P .

Noting that

d (1 cos )d 2 cos d cos d

xa a s

θθ

θθ θ

=+ = = ,

we have

d/d cos(/2)Fmgxsmg

θ=− =− ; because 2PO PMρ

′′ ′

4cos(/2)a θ= , the second equation of Euler gives the constraint force

cos cos

cos

2cos

Rmg

θθ

⎛⎞

−

⎜⎟

⎝⎠

(7.1.57)

If, in particular,

θπ=± , hence if the particle travels through the cycloid without

initial velocity, from one of the cuspidal points

P or P

′

, then it results

2cos 2

Rmg F

==−

;

(7.1.57')

in this case, we can state, after Euler, that the modulus of the constraint force is the

double of the modulus of the normal component of the own weight of the particle.

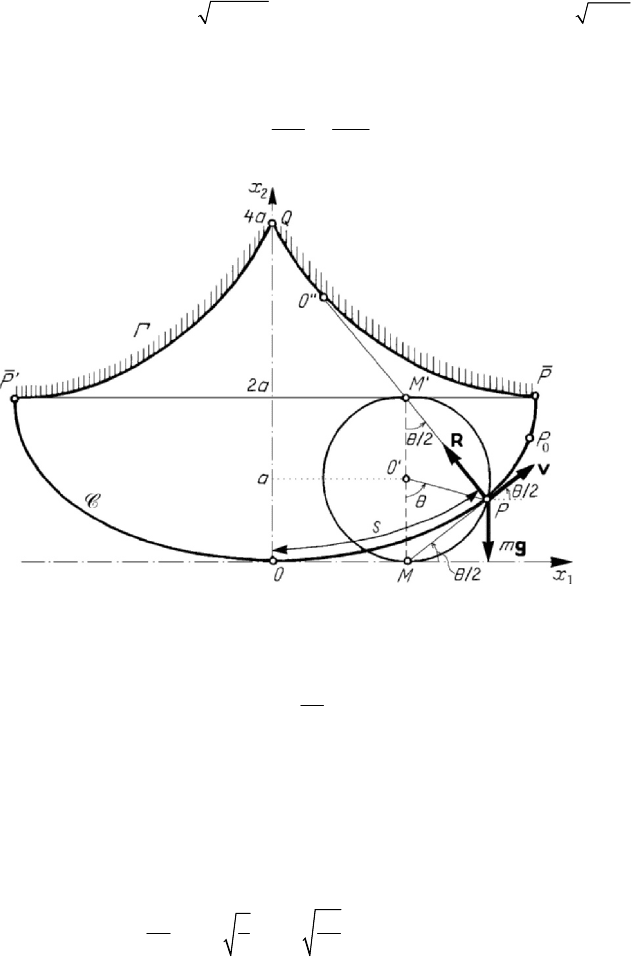
1.3.6 Motion of a heavy particle on a surface of rotation

Let us consider the motion of a heavy particle

P on a surface of rotation, the axis of

rotation of which is vertical (Fig.7.13). The own weight

mg of the particle and the

constraint force

R (the support of which pierces the

Ox -axis) act in the meridian

plane, their moments with respect to the symmetry axis vanishing; hence, we may write

the first integral of areas for the projection

′

of the particle P on the plane

Ox x ,

hence also for the particle

P , in the form (we use cylindrical co-ordinates)

rr Cθθ



(7.1.58)

where

(

)

rrt

()

tθθ=



. Because the constraint is scleronomic and the given

force is conservative, we may use also the first integral of energy

Problems of dynamics of the particle

435

()

222222

2vrr zv gzzθ=+ +=+ −



 ,

(7.1.58')

where

(

)

zzt

(

)

vvt= .

If the surface of rotation is given by

()rfz

(the equation of the meridian curve

C), then we may eliminate the functions ()rrt

and ()tθθ

between the equations

(7.1.58), (7.1.58'), obtaining the equation with separable variables

()

222

zfvgzz

′

+=+ −−

′

= ,

(7.1.59)

which determines the applicate

()zzt

by a quadrature; returning to the equation of

the surface of rotation and to the first integral of areas, we obtain the other co-ordinates

of the point

P . In the case of a circular cylinder of radius l , the equation (7.1.59)

becomes (

l= )

()

00 0

zv gzz

=+ −−

constC

(7.1.59')

Figure 7.13. Motion of a heavy particle on a surface of rotation.

in the case of a circular cone of equation

rkz

, constk

, we may write

()

22 2

kz v gz z

+=+−− , constC

(7.1.59'')

while in the case of a sphere of radius

l we obtain (

222

rzl

= )

()

(

)

22 2 2 2 2

2lz v g z z l z C=+ − −−

⎡⎤

⎣⎦

 , constC

(7.1.59''')

If we represent the surface of rotation by the equation

()zrϕ

, we may eliminate

the functions

()zzt= and ()tθθ

; it results the equation

MECHANICAL SYSTEMS, CLASSICAL MODELS

436

()

222

rvgz

ϕϕ

′

+=+ −−



′

constC

(7.1.60)

which specifies the radius

()rrt

by a quadrature too.

Eliminating the time, we obtain the equation of the trajectory of the point

′

in the

form

[]

{}

222

1()

2()

vgz C

ϕρ

θθ

ϕρ ρ

′

+− −

∫

(7.1.61)

where

()tθθ

; assuming that the surface is algebraic, Kobb has put in evidence the

cases in which the function

()rθθ

is expressed by means of elliptic functions.

In the case of a conservative force, the potential of which depends only on

r , the

problem may be solved only by quadratures too.

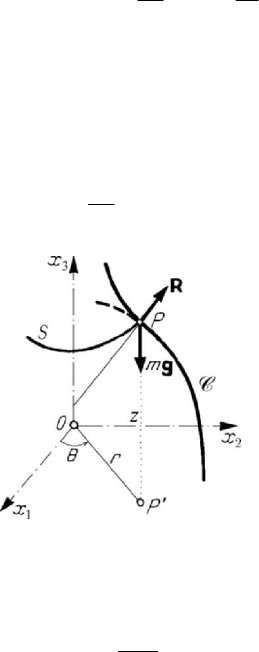
1.3.7 Spherical pendulum

A heavy particle which moves frictionless on a sphere of radius

l is called spherical

pendulum. The constraint may be bilateral or unilateral; in what follows we consider the

case of a bilateral constraint. We choose the equatorial plane of the sphere as plane

Ox x , the axis

Ox being along the descendent vertical; further it is convenient to use

cylindrical co-ordinates (Fig.7.14). If the constant

C of the first integral of areas

(7.1.58) vanishes, then

0θ



, hence constθ

; the trajectory of the particle is

contained in a meridian plane of the sphere, being thus a great circle of it. The spherical

pendulum is, in this case, a simple pendulum. If the constant

C is non-zero, then we

have to do with a non-degenerate spherical pendulum.

Figure 7.14. Spherical pendulum.

The equation (7.1.59''') becomes

()lz Pz= ,

()

(

)

2222

() 2Pz v g z z l z C=+ − −−

⎡⎤

⎣⎦

(7.1.62)

so that

Problems of dynamics of the particle

437

()

tt l

=±

∫

;

(7.1.63)

the first integral (7.1.58) allows to determine the angle

θ in the form

()

θθ

ζζ

=±

−

∫

(7.1.63')

In the two above formulae one takes the sign of

(

)

zzt

, assuming that 0z ≠ . If

0z = , then one takes into account the increasing or decreasing of z , starting from

the initial value

z .

First of all, we assume that

≠

 ; in this case

() 0Pz > (from (7.1.58), (7.1.58'),

(7.1.62) it results

(

)

22 2

0000

()Pz r r z=+). However, during the motion one must have

() 0Pz ≥ so that the integrals (7.1.63), (7.1.63') be real. Noting that

zl< (for

zl= we have the simple pendulum) and that ()P

−

∞=∞,

()Pl C±=− , it

results that the polynomial

()Pz is of the form

123

( ) 2 ( )( )( )Pz gz z z z z z

−− − −,

321

zlzzzl

−

∞< <− < < < <

(7.1.64)

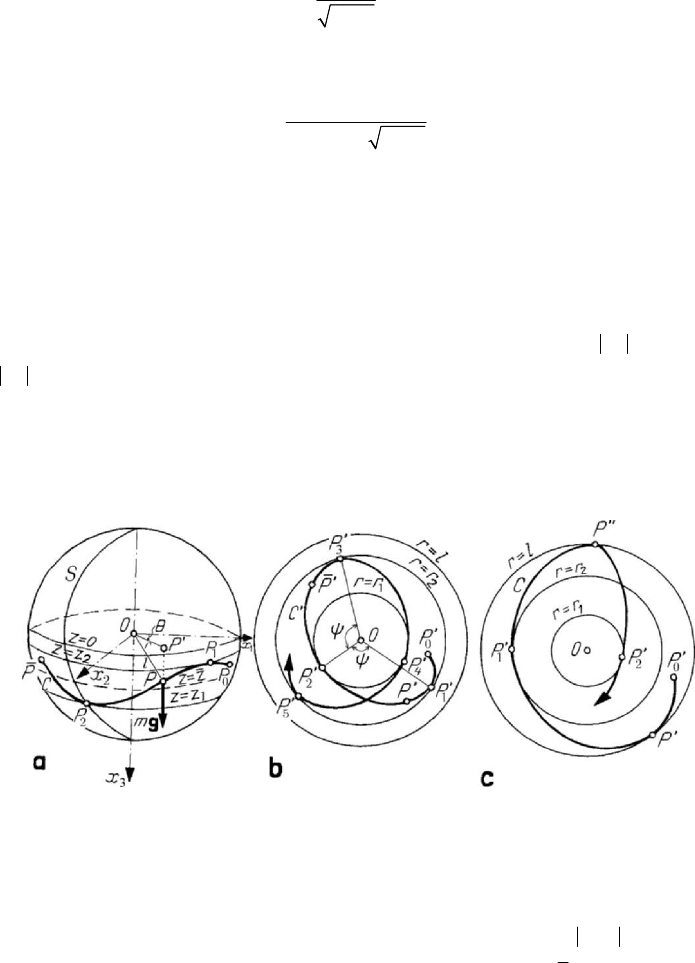
Figure 7.15. Spherical pendulum: zone of oscillation on the sphere (a); projection of the

motion on the equatorial plane: case

0z > (b); case

(c).

Hence, the particle

P oscillates on the spherical zone contained between the parallel

circles specified by

zz= and

(to have () 0Pz ≥ ) (Fig.7.15,a). Viète’s

formula allows to write

(

)

31 2 12

()zz z l zz+=−+ ; noting that

zz l< and

0z <

, it results that

0zz

. Hence, the parallel

()/2zz z z

=+ ,

equidistant to the parallels

and

, is always situated under the equatorial

circle (in the austral hemisphere). Departing from

, let us suppose that z decreases

(we have the sign – before the radical); the particle reaches

on the parallel

zz= ,

MECHANICAL SYSTEMS, CLASSICAL MODELS

438

where the trajectory has a horizontal tangent (at this point

 , but 0θ ≠



). Then,

the particle rotates about the vertical axis

Ox and reaches the point

P on the parallel

zz= , where the tangent to the trajectory is horizontal too; further, the particle reaches

the point

P on

zz= a.s.o. The particle P travels through the arc of trajectory



in the interval of time

()

∫

;

(7.1.65)

the same interval of time is necessary to travel through the arcs



PP ,



PP a.s.o. We

notice that the meridian planes of the points of contact of the trajectory with the

extreme parallels are planes of symmetry of this trajectory; indeed, for two points

and

of the same parallel z we have

()

θθ θ θ

ζζ

−=−=

−

∫

The necessary intervals of time to travel through the arcs



PP and



PP are equal too,

being given by

()

∫

We observe that after a time

T we find again the same values for z and z .

 , then we have

() 0Pz

too. Assuming that

()/2Pz

′

000

0gr z v=− ≠, the particle is launched from one of the extreme parallels (we have

zz= or

zz= ) with a horizontal initial velocity (hence, tangent to the respective

parallel); in the case of the parallel

one takes the sign + before the radical, while

if one departs from the parallel

the sign – is used. If

() 0Pz

′

= , then the

equation

() 0Pz = has a double root

000

/zzzgrv=== and one may write

22 2

2( )( )lz gz z z z=− − −



; noting that

zz> , one can have the latter relation

only for

constzz

. The trajectory of the particle is the parallel

zz= situated

in the austral hemisphere, because

0z >

. The spherical pendulum is reduced – in this

case – to a circular conical pendulum.

From (7.1.58), we notice that



has a constant sign; it results that the point P

′

(the

projection of the particle

P on the equatorial plane) rotates permanently in the same

direction around the centre

O , that direction being specified by the sign of the angular

velocity



, hence by the sign of C (if 0C > , then 0θ > too). The projection of the

trajectory

C of the particle P on the equatorial plane is the trajectory C

′

of the

projection

′

. If

0z ≥ , then the trajectory of this projection is contained between the

Problems of dynamics of the particle

439

concentric circles

rr l z== −,

, without any point

of inflection (Fig.7.15,b); the projection

′

gives the impression that it describes an

oval which is rotating in the direction of the motion (always in the same direction). One

can show that



12 23

...POP POP

′′ ′′

; Puiseux proved that these angles are always

greater than

/2π , while Halphen and then Saint-Germain showed that they are at the

most equal to

π . The angle



112

4POP POP

′

′′′

is the angle of precession and

emphasizes the “delay” of the point

′

with respect to the point

′

, so that the

trajectory of the point

′

cannot be closed. If

, then the corresponding parallel

is above the equatorial circle, but we have still

(because

0zz+>); the

trajectory of the projection

′

is tangent to the equatorial circle, and we may have also

inflection points. The properties which have been mentioned before are maintained

(Fig.7.15,c).

With the aid of the substitution

112

()zz z zu=− − and of the notation

()kzz=−

/( )zz− 1

2/ ( )lgzzτ =−, we may write the formula

(7.1.63) in the form

()()

222

uku

=±

−−

∫

(7.1.66)

wherefrom (we take

0t = and the sign + before the integral)

= ,

112

()sn

zz z z

=− − ;

(7.1.66')

hence, z is a doubly periodic function of

. The angular velocity ()tθ



is obtained as a

rational function of

sn( / )t τ ; one can integrate by decomposing in simple elements,

using Hermite’s method, obtaining thus the function

()tθ , which is not uniform. But

Tissot and then Hermite have state how to obtain the co-ordinates

z and

z as uniform

functions of

. Greenhill showed that, in the case in which the point

is in the plane

0z =

, the initial velocity being tangent to the equatorial circle, then

and

are

given by pseudoelliptic integrals, which may be expressed by elementary functions.

The constraint force

R (Fig.7.14) is given by

RFmvρ=− +

; noting that

lρ = and /

Fmzl=− , we get

(3 2 )

Rvgzz

=+−

⎡

⎤

⎣

⎦

(7.1.67)

The force

is directed towards the centre

( 0R > for

0z >

) if the particle is in

the austral hemisphere; if

P is in the boreal hemisphere (

), then it is possible to

have

0R = for a parallel z . In the case of a unilateral constraint (the particle is at the

extremity of a perfectly flexible and inextensible thread), after passing the parallel

MECHANICAL SYSTEMS, CLASSICAL MODELS

440

zz=

, the particle may move further on an osculating parabola to the previous

trajectory on the sphere, in a vertical plane, till it meets again the sphere; then, the

motion is continued in conformity with the laws established before. In the case of a

bilateral constraint, the constraint force may change its sign, being directed towards the

interior of the sphere. We notice that, in general, the resultant of the forces

R and mg

is tangent to the trajectory at the point

P , hence it is contained in the osculating plane

to the curve at that point. If

R0, then the osculating plane is vertical; in this case,

the trajectory of the projection

′

on the equatorial plane has an inflection point at this

point. In the case of the circular conical pendulum, the constraint force becomes

000

//Rmglz mlvr== ; the projection of this force on the equatorial plane is

00000

//Rr l mv r mr θ==



, hence a centripetal force.

Projecting the equation of motion on the Cartesian co-ordinate axes, we obtain

mx R

=−

mx R

=−

mx mg R

=−

;

in the case of small oscillations around the position

0xx

xl=

, which is a

stable position of equilibrium, we notice that

()

222

312

1 ...

xlxxl

⎛⎞

=−+=− +

⎜⎟

⎝⎠

In a first approximation

(we neglect the second term with respect to unity), and

we may assume that the motion takes place in the plane tangent at the lowest point of

the sphere. In this case, the third equation of motion leads to

Rmg

; the first two

equations may be written vectorially in the form



rr0

(7.1.68)

where

r is the vector radius in the equatorial plane. One obtains thus an elliptic

oscillator, which will be studied in Chap. 8, Subsec. 2.1.1. The motion is periodic and

the trajectory is an ellipse, which may be travelled through in an interval of time given

2/Tlgπ= (the period corresponding to a simple pendulum). An approximation

of second order has been considered by Tisserand; other methods of approximation

have been used by Resal and Sparre.

2. Other problems of dynamics of the particle

After considering the problems of Abel and Puiseux and of tautochronous motions,

one deals with the motion on a brachistochrone or on a geodesic curve, as well as with

other cases of motion. Some results concerning the stability of the equilibrium of a

particle are given too.