Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

Problems of dynamics of the particle

421

a confirmation that the trajectory is rectilinear. Choosing this trajectory as

Ox -axis, we

obtain

(

)

vfgttv=− − + ,

()()

0000

xttvttx

−−+−+,

tttt

∗

≤≤ = +

(7.1.35'')

where the time

∗

is given by the condition

(

)

0vt

∗

; timing the time t

∗

, one may

obtain – experimentally – the coefficient of sliding friction

. After a time

∗

− , the

particle travels through the distance

/2lv fg= ; inversely, measuring

one

determines the initial velocity

2vfgl= .

(7.1.35''')

We may thus estimate the velocity of a car if we know the braking distance

l .

If the initial velocity vanishes (

), then it results 3/2θπ

, so that the

sliding of the particle on the inclined plane takes place along the line of greatest slope,

the trajectory being rectilinear; using the above equations, the acceleration at a given

moment is specified by (along the

Ox -axis)

sin( )

cos

αϕ

−

=−

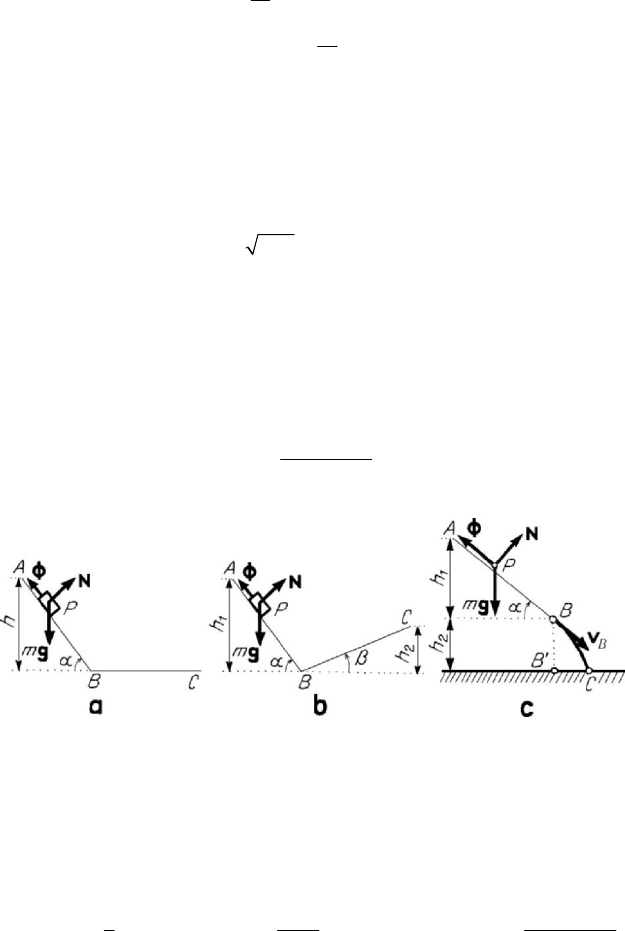
Figure 7.7. Motion of a heavy particle constrained to sliding friction on an inclined plane:

motion continues on a horizontal plane (a); motion continues on

an inclined plane (b); silo’s problem (c).

Applying the theorem of kinetic energy in a finite form (6.1.48''), we obtain the velocity

at the point

B , assuming that the body, modelled as a particle, departs from A without

initial velocity (Fig.7.7,a); noting that

T = ,

Tmv= ,

sin( )

(sin cos )

sin sin cos

Wmg f mgh

αϕ

αα

ααϕ

−

=−=

it follows

MECHANICAL SYSTEMS, CLASSICAL MODELS

422

sin( )

sin cos

vgh

αϕ

−

(7.1.36)

In the absence of frictions,

vgh=

, as in the case of a free falling along the

vertical (Torricelli’s formula). Applying further the theorem of kinetic energy, we see

that the body moves on the horizontal line till the point

C , so that (Fig.7.7,a)

sin( )

sin sin

BC h

αϕ

−

;

(7.1.36')

in the case of vanishing friction,

C tends to infinity. If the plane BC makes the angle

with the horizontal line, the body moves till the height

h , given by (Fig.7.7,b)

21 1

sin sin( )

hh h

βαϕ

αβϕ

−

;

(7.1.36'')

in the case in which the friction is vanishing, we have

. This is the problem of

the sledge. If, from the point

B , the particle is falling freely till the point C (the

problem of the silo, Fig.7.7,c), then the motion takes place along a parabola, so that

tan

cos

hBCBC

′′

(7.1.36''')

1.3 Pendulary motion

As we have seen in Subsec. 1.2.4, a heavy particle constrained to stay on a fixed

curve has an oscillatory motion; such a motion is called also a pendulary motion. In

what follows, we consider the case of a curve in a vertical plane, in particular the case

in which the curve is a circle, an ellipse or a cycloid; we study then the general case of

motion, as well as the case of small displacements in the neighbourhood of a stable

position of equilibrium. Starting from the motion of a heavy particle on a surface of

rotation, we present the general problem of the spherical pendulum too.

1.3.1 Simple pendulum

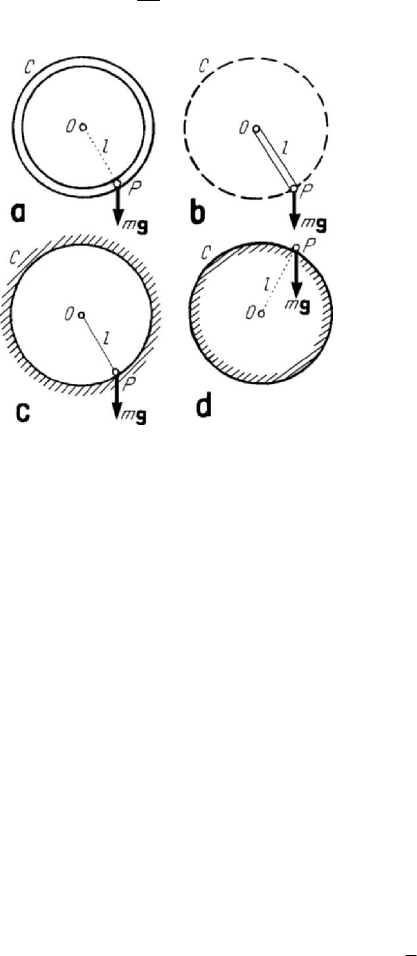
A simple pendulum (or mathematical pendulum) is a heavy particle which moves

without friction on a circle

C of radius l , situated in a vertical plane. The constraint

may be bilateral (e.g., a ball modelled as a particle constrained to move in the interior of

a circular tube (Fig.7.8,a) or a ball linked to the centre

O of the circle by an

inextensible and incompressible bar

OP , of negligible mass with respect to that of the

particle (Fig.7.8,b)) or unilateral (e.g., a ball linked to the centre

O by an inextensible

and perfectly flexible thread (Fig.7.8,c) or a ball constrained to move on a whole

cylinder, which has a horizontal axis (Fig.7.8,d)).

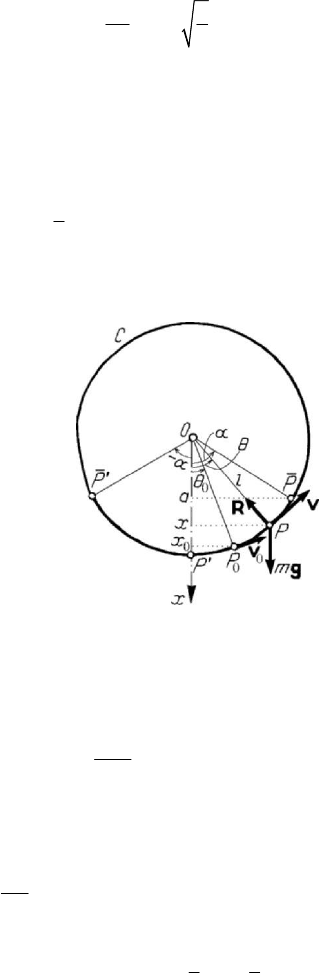
If we choose the

Ox -axis in the same direction as that of the gravity acceleration g

(Fig.7.9), then the theorem of kinetic energy in finite form, applied between the points

P and P , allows to write

Problems of dynamics of the particle

423

22 2

00 0 0

2( ) 2 (cos cos) 2( )vv gxxv gl gaxθθ=− −=− − =− −,

=−,

(7.1.37)

Figure 7.8. Motion of a heavy particle constrained to stay on a circle in a vertical plane: bilateral

constraint (a,b); unilateral constraint (c,d).

where

vlθ=



is the modulus of the initial velocity (for the sake of simplicity, we will

say the initial velocity) at the point

(corresponding to the results in Subsec. 1.2.4).

The equation

xa= is that of a straight line which may be reached by a particle

launched up, along the local vertical, with the initial velocity

v ; the motion is

characterized by the constant

a in the case of a bilateral constraint. Indeed, if the

straight line

xa= pierces the circle

(

lal

−

), then the motion is oscillatory, if

this line is tangent to the circle (

−

), then the motion is asymptotic, while if the

line does not pierce the circle (

−

), then the motion is circular. We notice that for

al=

we have

0v =

, corresponding a stable position of equilibrium; we cannot have

al> . From (7.1.37) it results that the velocity

vlθ



may vanish for an angle given

cos cos / 2vglθθ=− or by

()

222

sin ( / 2) sin /2 / 4vglθθ=+. This

condition can never be satisfied if

4vgl> (or

4θω>



/glω = ), the motion

being circular. If

4vgl< , then the condition may be fulfilled for some values of the

angle

θ , hence for some initial positions, e.g., for

0θ

; in this case, the motion is

oscillatory. If

4vgl= , then we must have

0θ

, the motion being asymptotic.

First of all, let us suppose that the motion is oscillatory; we denote

cosal α=

where

0 απ

< is the angle corresponding to the limit position

(for which

0v = ) of the particle P , specifying thus the amplitude of the motion. The relation

(7.1.37) becomes

MECHANICAL SYSTEMS, CLASSICAL MODELS

424

2(cos cos)θωθ α=−



;

(7.1.38)

differentiating with respect to time, we may also write (we suppose

0θ

≠



)

sin 0θω θ



(7.1.38')

This equation (called the equation of the mathematical pendulum) is often encountered

in problems of mechanics in one of the two equivalent forms mentioned above; in fact,

the relation (7.1.38) corresponds to a first integral of the equation of motion (7.1.38').

The particle departs from the initial position

P with the velocity

v and travels up

on the circle with a velocity which diminishes in intensity; at the extreme position

P ,

the velocity vanishes. Returning on the travelled arc of circle, the velocity increases; the

particle passes through the initial position

and reaches the lowest point P

′

of the

trajectory, where it has the maximal velocity; then the velocity decreases till the particle

reaches the point

′

for which θα

− . The particle returns then to P

′

and

a.s.o.

Hence, the motion is oscillatory. From the relation (7.1.38), we also notice that the

velocity

()vt depends only on the position of the particle, being a periodic function of

this position (of angle

θ ); integrating this equation with separate variables, we may

write (during the motion we have

cos cosθα> )

cos cos

ϑα

−

∫

(7.1.39)

where

corresponds to the position at the arbitrary moment

(which may be

different from the initial moment

t ). Hence, one can see that the interval of time

tt− depends only on the positions corresponding to the two moments; it results that

the oscillatory motion is periodical, of period

T . We notice too that changing the

direction of motion on the arc of circle the sign of the velocity changes; its modulus

remains the same when passing through the same point, so that the arc



′

is travelled

through in an interval of time

/2T . Because the relation (7.1.38) is even with respect

θ , it results that, at points symmetric with respect to the Ox -axis, we have the same

velocity (travelling up or down); hence, the arc



′

is travelled through in a quarter of

period. In this case, the period

is given by the relation

22 d

cos cos

ϑα

−

∫

(7.1.39')

Observing that

cos cos 2 sin ( /2) sin ( / 2)θα α θ−= −

⎡

⎤

⎣

⎦

and denoting

sin( / 2)θ sink ϕ

, sin( / 2)k α= , we may write

1sin

−

∫

(7.1.40)

Problems of dynamics of the particle

425

where

ϕ is specified by the relation

(

)

sin /2 sinkθϕ= ; denoting sin zϕ = , we

may also write

()( )

222

ζζ

−−

∫

(7.1.40')

where

z is specified by the relation

sin zϕ

. Introducing, after Legendre, the

elliptic integral of the first kind

()( )

sin

22 2 22

(,)

1sin 1 1

kzkz

ϕϕ

−−−

∫∫

(7.1.41)

where

ϕ is the amplitude, while k is the modulus of the integral, we obtain

[]

(,) ( ,)tt F k F kϕϕ

=+ −

(7.1.40'')

Denoting

utω= , we may write

(,) ( ,)uu F k F kϕϕ−= − ,

(7.1.40''')

where

utω

. Taking

, with no loss of generality, and assuming that

0θ =

, there results

(

)

000 0

,0zuF kϕϕ=== =

, so that

(,)uF kϕ

(7.1.42)

As it was noticed by Abel, it is easier to express the angle

ϕ as a function of the

variable

u , in the form

sin sn uϕ

, (7.1.42')

where

sn is the symbol of the elliptic sine (the amplitude sine), one of the Jacobi’s

elliptic functions; analogously, one may use the elliptic cosine (the amplitude cosine),

denoted by the symbol

cn ( cos cn uϕ

Starting from the formula (7.1.39'), the period of the motion is given by

()( )

/2 1

22 2 22

d44 4 d

()

1sin 1 1

TKk

kzkz

ωω ω

== =

−−−

∫∫

ω =

(7.1.43)

where

() ( /2,)Kk F kπ= is the complete elliptic integral of the first kind. Observing

that

1k <

, one obtains the development into series (we use Newton’s binomial series)

MECHANICAL SYSTEMS, CLASSICAL MODELS

426

()

1/2

22 2 2

(2 )!

1 sin 1 sin

2(!)

ϕϕ

∞

−

−=+

∑

This series is absolute and uniform convergent on the interval

[

]

0,2π , and we may

integrate it term by term; taking into account Wallis’ formula

(2 )!

sin d

2(!)

ϕϕ=

∫

(7.1.44)

one obtains the period

[]

(2 )!

21 sin

2(!)

∞

⎧

⎫

⎨

⎬

⎩⎭

∑

(7.1.43')

Because we may develop

sin( /2)α into an absolute convergent series with respect to

α too, we obtain also for T such a development, of the form

2 1 ...

16 12

αα

⎛⎞

=+++

⎜⎟

⎝⎠

(7.1.43'')

We observe that the ratio between the second and the first term of the series is equal to

/16α

; as well, the ratio between the third and the second term is given by

(11/12) /16α a.s.o. Hence, the series is rapidly convergent; practically, we may take

⎛⎞

⎜⎟

⎝⎠

(7.1.43''')

0.4α = (it corresponds to the angle 22 55 06

′

′′

), then the correction brought by the

second term of the development is not greater than

%1 . The astronomic watches have

amplitudes of

130

′

° , corresponding a correction of approximately 0.05‰ . In general,

the period

depends on the angle α , but is independent of the mass m of the

particle. In the case of small oscillations around a stable position of equilibrium (in

Chap. 4, Subsec. 1.1.7 we have seen that the point

′

represents a stable position of

equilibrium), the equation (7.1.38') has the form (we approximate

sin θ

)

0θωθ



(7.1.45)

wherefrom

() cos( )ttθαωϕ

− ,

(7.1.45')

the angle

ϕ being specified by the initial conditions, while the period is given by

Galileo’s formula

Problems of dynamics of the particle

427

;

(7.1.45'')

we notice that this result (intuited by considerations of homogeneity in Chap. 1, Subsec.

2.2.4) approximates the development into series (7.1.43''). The period

T thus obtained

depends on the length

l of the pendulum and on the gravity acceleration g at the

respective place on Earth’s surface. Because this period does not depend on the

amplitude

α , we say that the respective motion is isochronic (the small oscillations

around a stable position of equilibrium take place in the same interval of time). A

particle

P left free from

without initial velocity reaches the lowest position P

′

in a

time equal to

/4T , which does not depend on the initial position (angle α ); in this

case, this motion is called tautochronous.

Figure 7.9. Simple pendulum.

The equation of motion along the principal normal to the trajectory is written in the

form (Fig.7.9)

cos

Rmg

θ=− ,

where

R is the constraint force directed towards the centre

; taking into account

(7.1.37), we get

(3 2 ) (3 cos 2 cos )

Rxamg

θα=−= −.

(7.1.38'')

One obtains

max

(3 2cos )Rmg α=− . The constraint force diminishes if the particle

P becomes closer to the extreme positions P and P

′

; it vanishes for 2/3xa= , then it

changes of sign (in case of a bilateral constraint). From (7.1.37) too, we notice that

xa> during the motion; the constraint force vanishes if 2/3aa> , hence for 0a < .

On the other hand,

2/3al>− , so that 3/2al>− ; it results that the constraint force

MECHANICAL SYSTEMS, CLASSICAL MODELS

428

vanishes only for

3/2 0la−<< (hence, cos 0α

and /2απ> ). Replacing the

expression of

a , we find the condition

()

00 0

232gx v g l x<< +

(7.1.46)

which must be fulfilled by the initial velocity, at the initial position, so that the particle

be capable to reach the position (in any case, above the horizontal diameter) at which

the constraint force may vanish. In particular, if

, then we have

25gl v gl<< .

(7.1.46')

Figure 7.10. Simple pendulum; unilateral constraint.

If the constraint is unilateral, being obtained with the aid of a perfect flexible,

torsionable and inextensible thread, then that one is tensioned if

R is positive. At the

moment at which

0R = (at the point Q , Fig.7.10), the particle leaves the circle and

moves as a free particle acted upon by its own weight. It will describe thus an arc of

parabola of vertical axis, which is connected to the circle at the point in which the

constraint force vanishes; the particle moves further till it meets again the circle at the

point

Q . If

02vgx≤≤ , then the motion is oscillatory even in the case of a

unilateral constraint.

1.3.2 Circular and asymptotic motion

4vgl>

, hence if al

− , then the equation (7.1.38) takes the form

(

)

22 2

2(cos ) 2 2sin

lglaglal

θθ

=−=−−



(

)

2( )1 sin

gl a k

=−− ,

(7.1.47)

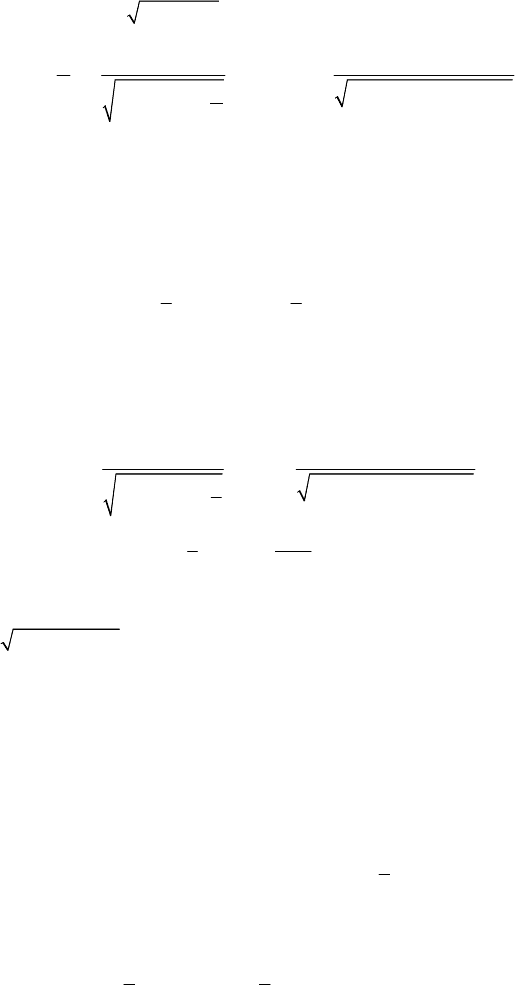
Problems of dynamics of the particle

429

where

2/( )klla

− ,

01k

< ; hence, the angular velocity θ



(the velocity v

too) never vanishes, and maintains its sign. The motion of the particle becomes circular

and periodic (the velocity depends only on the position).

Denoting

2/ 2( )lglaτ =−, we get

()( )

222

1sin

tt t

ζπϑ

ζζ

=+ =+

−−

−

∫∫

(7.1.47')

where

θ corresponds to an arbitrary moment

t (in general, distinct from the initial

moment) and where we have made a change of variable

sin( / 2)z θ

, denoting also

sin( /2)z θ=

. Assuming that

0t θ

, it results

, so that we may use

the equations

sin sn

= , cos cn

= ,

(7.1.47'')

where we have introduced the notation

/utτ

. The period

in which the whole

circumference is described is equal to twice the time necessary to arrive from the lowest

point (

xl= ) to the highest one (xl

− ); hence (

0t θ

)

()( )

222

1sin

zkz

ττ

−−

−

∫∫

(

)

(

)

113

1...

224

πτ

⋅

⎡⎤

=+ + +

⎢⎥

⋅

⎣⎦

(7.1.47''')

The corresponding constraint force is given by the same relation (7.1.38''); if

()

32vglx>+, then the constraint force does not vanish and remains with its

positive sign, and if the relation is an equality, then the constraint force vanishes at the

highest point (

xl=− ). We notice that

max

(3 2cos )Rmg α=− ,

min

(3 2cos )Rmg α

−+ ,

max

min

5RRmg

−=.

(7.1.48)

al=−, hence if

4vgl= , then the equation of motion becomes

22 22

2(1cos)4 cos

θω θω

=+=



;

(7.1.49)

by integration, one obtains

()

tan ( ) tan ( )

θπ θ π

−

+= + .

(7.1.49')

MECHANICAL SYSTEMS, CLASSICAL MODELS

430

For

t →∞ we have θπ→ ; the particle reaches the highest point on the trajectory (a

labile position of equilibrium) in an infinite time; the respective motion is called an

asymptotic motion. The constraint force is given by

(3 2 ) (2 3cos )

Rxlmg

θ=+=+

;

(7.1.49'')

in this case

max

5Rmg= , for 0θ

. The minimal constraint force

min

Rmg=− , for

θπ= , can be obtained only in the case of a bilateral constraint; in the case of a

unilateral one, beginning with the point

Q , determined by 2/3xl

− (hence, by

cos 2 / 3θ =− , corresponding to 131 48 37θ

′

′′

° ), the motion is on an arc of parabola.

Analogously, one may study the problem of the swing, which may be modelled as a

simple pendulum with a thread of length variable in time (

()llt

1.3.3 Motion of a simple pendulum in a resistent medium

Introducing the resistance

R of the medium, tangent to the trajectory and of

direction opposite to that of the velocity, and writing the equation of motion along the

tangent, one obtains

sinml mg Rθθ

−−



(7.1.50)

Considering a resistance proportional to the velocity (viscous damping), of the form

2Rmlλθ=



, 0λ > , in the case of small oscillations ( sin θθ

≅

), the equation (7.1.50)

becomes

20θλθωθ

 

;

(7.1.51)

assuming that

ωλ>

and denoting

222

μωλ=−, we obtain the general integral

() e ( cos sin )

tAtBt

θμμ

−

(7.1.51')

where the constants

A and B may be determined by the initial conditions

(

)

tθθ= ,

()

tθθ=



. We may thus write (for the sake of simplicity, we assume that

0t = )

()

000

() e cos sin

tt t

θθμλθθμ

−

⎡⎤

=++

⎢⎥

⎣⎦



(7.1.52)

()

000

() e cos sin

tt t

θθμωθλθμ

−

⎡⎤

=−+

⎢⎥

⎣⎦

 

(7.1.52')

If, in particular, we have

0θ



, then the particle departs without initial velocity from

the point

P and reaches the point

P , where the velocity