Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

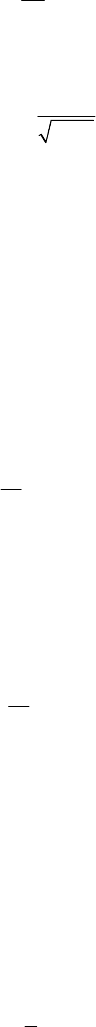
Dynamics of the particle with respect to an inertial frame of reference

391

(

)

()

ϕ==



and we obtain

()

ϕη

−=±

∫

(6.2.18')

where the position of the particle at the initial moment has been emphasized. The sign

taken in this formula is that of the generalized velocity

q (the sign of the initial

velocity, which is preserved if

q

does not vanish); if

q

vanishes, then the velocity v

vanishes too, while the sign is specified by the sense of the velocity v , hence by the

sense of the tangential component of the given force

F .

The trajectory and the velocity of the particle being determined, in the case of a fixed

curve, as well as in the case of a movable one, we may put in evidence the constraint

force

R , by calculating the scalars

λ and

λ from two of the equations (6.2.16') (the

system (6.2.16') is – in this case – compatible).

Projecting the equation of motion (6.2.5) on the axes of Frenet’s intrinsic frame, in

case of stationary constraints, we obtain

(,;)mv ms F sst



 

mFR

νν

, 0FR

ββ

= .

(6.2.19)

The first of these equations does not contain the constraint force, so that it determines

the motion of the particle along the trajectory (as a matter of fact, multiplying both

members of the equation by

ds , we get the theorem of kinetic energy), while the other

two equations give the components of the constraint force in the plane normal to the

trajectory (in a simpler form as that previously mentioned)

RFm

νν

=− +

, RF

ββ

− .

(6.2.20)

The first equation (6.2.19) shows that the law of motion does not change if the curve is

deformed without changing its length or by modifying the force

F , but maintaining its

tangential component (only the constraint force is changing); in particular, we may

transform the curve into a straight line, reducing the problem to the study of a

rectilinear motion.

F is a conservative force, deriving from a simple potential ()UU

r or from a

generalized potential (the simple part of which is

()UU

r ), then we may write a

conservation theorem of energy in the form (6.1.55) or (6.1.55'); the component of the

constraint force along the principal normal is thus of the form

()RF Uh

νν

=− + +

(6.2.20')

MECHANICAL SYSTEMS, CLASSICAL MODELS

392

and is obtained without knowing the motion of the particle on the trajectory (in case of

a generalized potential we replace the function

U by the function

U ).

In the general case of rheonomic constraints we may use Lagrange’s equations

(6.1.24'); because we have only one generalized co-ordinate

q , we obtain the

differential equation (

(;)qt=rr )

(,;)

Qqqt

tq q

∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠



(6.2.21)

where

Tmq

∂∂

⎛⎞

⎜⎟

∂∂

⎝⎠



, (,;)Qt

∂

⋅

∂



Frr

(6.2.21')

the unknown function being

()qqt

. In particular, we may consider (;)st=rr ,

where

s is the curvilinear co-ordinate along the curve C ; a scalar product of the

equation of motion (6.2.5) by the unit vector

d/ds

, tangent to the curve C ,

leads to (

0⋅=R τ )

⋅

=⋅=



τ ;

but

∂



∂

=++

∂





 

ττ

so that the equation of motion, which is a generalization of the equation (6.2.19),

becomes

ms F

∂

+⋅=

∂



τ ,

(6.2.22)

where the unknown function is

()sst

2.2.2 Motion of a particle constrained to stay on a surface

Let

be a particle in motion on a smooth movable or fixed surface

(Fig.6.8) of

equation (6.2.3) or (6.2.3'). The constraint force is given by (6.2.6) and the equation of

motion becomes

gradmfλ



; (6.2.23)

in components, we may write

,ii i

mx F fλ

+ , 1, 2, 3i

. (6.2.23')

Dynamics of the particle with respect to an inertial frame of reference

393

The equations (6.2.3) and (6.2.23') form a system of four scalar equations for the three

unknown functions

()

xxt= and for the parameter λ , which specifies the constraint

force. Thus, the equations (6.2.23') allow to write

Figure 6.8. Motion of a particle constrained to stay on a surface S.

11 22 33

,1 ,2 ,3

mx F mx F mx F

fff

−

−−

  

Adding also the equation (6.2.3), we may determine the trajectory of the particle; the

parameter

λ is then given by any of the equations (6.2.23').

In the case of a unilateral constraint (case in which the particle may leave the surface,

remaining on one part of it), one must take into consideration the direction of the

constraint force

. Thus, if the force

is directed towards the part in which the

particle may leave the surface, that one will remain on the surface. We notice that the

force

is directed towards the part of the surface for which

≷

0λ ≷

; hence,

the particle remains on the surface only if the parameter

λ maintains its sign.

Consequently, if this parameter vanishes and changes of sign, then the particle leaves

the surface and moves – further – as a free particle.

In the case of a rheonomic constraint, we may write

grad d d 0

⋅



r ,

and the real work of the constraint force is given by

ddgraddd

Wfftλλ=⋅ = ⋅ =−



Rr r ;

indeed, the real displacement of the particle is not tangent to the surface frozen at the

moment

t , while the constraint force R is normal to this surface at the point P . If the

constraint is scleronomic (or – at least – catastatic), then

, and the theorem of

kinetic energy can be written in the form (6.1.48); because the particle is constrained to

stay on a surface, and has two degrees of freedom, it is necessary one equation more to

can specify the motion.

Using Darboux’s frame, we may write, in case of a fixed surface,

MECHANICAL SYSTEMS, CLASSICAL MODELS

394

mv F



mFR

+ ,

;

(6.2.24)

the first and the last equation determine the motion corresponding to the two mentioned

degrees of freedom, while the second equation gives the constraint force

RFm

=− +

(6.2.25)

If the force

F is conservative, deriving – for instance – from a simple potential

()UU= r , we may use the formula (6.1.55), and the constraint force is given by

()

RF Uh

=− + +

(6.2.25')

In the case of a given zero force (

F0), the first equation (6.2.24) shows that the

motion of the particle is uniform (the magnitude

v of the velocity is constant in time).

The component of the acceleration along the tangent to the trajectory vanishes, so that

the acceleration is directed towards the principal normal

to the trajectory. The second

equation (6.2.24) emphasizes (

) that the acceleration vector is normal to the

surface

; hence, at the point

, the principal normal to the trajectory of the particle

has the same support as the normal to the surface

(

=n0

). The last equation

(6.2.24) shows that (

F = ) the geodesic curvature vanishes; hence, the trajectory of

the particle

P is a geodesic of the surface S , the motion being uniform. This result

may be put in connection with the principle of inertia, the straight line being a geodesic

of the space

E ; in this case,

ρ →∞, while 0R

. It results the constraint force in

the form

(6.2.26)

where

v is the magnitude of the initial velocity. For instance, a particle which is

constrained to stay on a fixed sphere and is acted upon by a zero force describes a great

circle of it.

We notice that the trajectory is a geodesic if the necessary and sufficient condition

F = is fulfilled, hence if the force F belongs to the osculating plane of the

trajectory (determined by the unit vectors

and

=n0

); in this case, the

motion is uniform only if

, hence if the given force is normal to the surface S .

If the particle has a uniform motion on a geodesic circle (

1/ const

, in the sense

of Darboux), then we have

const

, 0F

, so that the given force is normal to

the trajectory, its projection on the tangent plane being constant during the motion. As

well, if

− during the motion, then the trajectory is an asymptotic line of the

surface.

Dynamics of the particle with respect to an inertial frame of reference

395

As in the preceding subsection, in the case of rheonomic constraints we may use

Lagrange’s equations (6.1.24') in the form (we have two generalized co-ordinates

and

q , so that

(

)

,;qqt=rr )

1212

(, ,, ;)

Qqqqqt

tq q

αα

∂∂

⎛⎞

−=

⎜⎟

∂∂

⎝⎠





, 1, 2α

(6.2.27)

where

Tm q q

qq t

∂∂∂

⎛⎞

=++

⎜⎟

∂∂∂

⎝⎠



rrr

, (,;)Qt

∂

=⋅

∂



Frr

;

(6.2.27')

the unknown functions

()qt and

()qt may be – eventually – curvilinear co-ordinates

s and

s on the surface

. In this case, taking into account the formula (6.1.24''') and

the results in Chap. 5, Subsec. 1.2.3, the equations of motion read

()

ms m s s g Q s s

αβ

αγ

ββ

βγ

⎧⎫

⎨⎬

⎩⎭

   ,

∂

=⋅

∂

,1,2αβ

(6.2.28)

and the unknown functions are

()sst

and

()sst

. Making

0QQ==

and

noting that one can take the time

proportional to the curvilinear co-ordinate s on the

trajectory (the motion is uniform), we find the equations of the geodesic curves

sss

αγ

βγ

⎧⎫

′′ ′ ′

⎨⎬

⎩⎭

, 1, 2α

(6.2.29)

where

/sss

αα

′

∂∂, 1, 2α = .

We have seen that the conservation theorem of the mechanical energy allows – in the

conditions in which this theorem takes place – to determine easily the constraint force,

if the trajectory of the particle is known. In what concerns the conservation theorem of

moment of momentum, the condition

( ) grad

λ×+ =×+× =rFR rF r 0

must hold; this condition is fulfilled for any

λ if

=rF 0 and grad

=r0. We

obtain a scalar first integral if the components of the two moments along one of the axes

(for instance,

Ox ) vanish. Thus, we start from

1,2 2,1

0xf xf

−

= ; the associate system

of differential equations

123

ddd

xxx

−

leads to the integrals

12 1

xxC+=,

, so that

(

)

123

fx x x

+=.

Hence, the surface

S must be a surface of rotation (with

Ox as symmetry axis);

MECHANICAL SYSTEMS, CLASSICAL MODELS

396

indeed, the support of the constraint force intersects – at any moment – the rotation

axis. If the particle

P is constrained to stay on a surface of rotation, while the force F

is coplanar with the symmetry axis of the surface, then we may write a first integral of

the form (6.1.54').

2.2.3 Motion of a particle subjected to constraints with friction

In the case of a constraint with friction, the constraint force R has not only the

normal component

N , which does not allow the particle to leave the constraint, but also

a tangential one

≠T0, which hinders the particle to move in the frame of this

constraint. As in the static case, considered in Chap. 4, Subsec. 1.1.8, in what follows

we use the Coulombian model introduced in Chap. 3, Subsec. 2.2.11, for the force of

friction; we assume that the constraints are holonomic and scleronomic. The force of

friction is tangent to the rough surface or curve on which stays the particle, its direction

being opposite to that of the motion.

In the case of a particle constrained to stay on a rigid fixed or movable curve

C , of

equations (6.2.1), the equation of motion reads



rFNT

. (6.2.30)

We introduce also the relations

TN,

=−

(6.2.31)

where

v is the relative velocity of the particle; we notice that vers vers

+=Tv0.

If the particle is constrained to stay on a rigid fixed or movable surface

S , of equation

(6.2.3), then the equations which determine the unknown quantities will be of the form

(6.2.30) and (6.2.31) too. The relative velocity is given by

−vvv, where

() ()

ttQP=+×





vv ω

is the velocity of transportation of the surface (or of the

curve);

Q is a point of the surface (or curve), while ()t

is the instantaneous rotation.

Eliminating the force of friction

T , we obtain the vector equation

mNfN

−

=+ −

−



rF n

(6.2.32)

where

vers grad

=n , or the vector equation

11 22 1 2

mNNf

−

=+ + − +

−



rF n n N N

(6.2.32')

where

vers grad

αα

n , 1, 2α

. If the surface

(or the curve

) is fixed, then

the velocity of transportation vanishes (

v0).

If we consider the motion on a fixed curve with respect to Frenet’s frame, then we

get

Dynamics of the particle with respect to an inertial frame of reference

397

signmv F fN v

=−



mFN

νν

, 0 FN

ββ

+ ,

(6.2.33)

with

NNN

; the equations (6.2.33) and (6.2.1') determine thus the unknown

functions

()

xxt= , 1, 2, 3i = , as well as the components ,NN

of the constraint

force. Eliminating the constraint force, we may write the equation

sign

mv mv F f F m F v

τν

⎛⎞

==−+−

⎜⎟

⎝⎠



(6.2.34)

which gives the velocity

()vvs

. In the case of a plane curve, the force F belonging

to the respective plane, we have

and we get

(

)

d2 d

mv m F f m F

τν

⎛⎞

== −

⎜⎟

⎝⎠

∓

(6.2.34')

where the sign corresponds to a direction of the constraint force opposite to the motion.

Integrating, we have

()vsϕ= ,

(6.2.35)

where

[]

2() 2() 2()

() e e e ( ) ( )d

fs fs f

sC F fF

ψψψσ

τν

ϕσσσ=+ +

∫

∓∓

(6.2.35')

with

()

sψ

∫

, constC

(6.2.35'')

Hence, we obtain

()

ϕσ

−=

∫

(6.2.35''')

the motion of the particle on the fixed curve

C being thus specified; returning to the

equations of motion (6.2.33), we emphasize the constraint force too.

In the case of a particle constrained to move on a fixed surface

S , we introduce

Darboux’s trihedron and find the equations

mv F fN

=−



mFN

+ ,

= ;

(6.2.36)

MECHANICAL SYSTEMS, CLASSICAL MODELS

398

these three equations, together with the equation (6.2.3'), form a system of four

equations for the unknown functions

()

xxt

1, 2, 3i

, and the constraint force

N . Eliminating the constraint force between the first two equations, we get a new

equation which, together with the third equation (6.2.36), constitutes a system of two

differential equations for the unknown curvilinear co-ordinates

()sst

αα

1, 2α =

on the surface

S ; thus, the relation (6.2.3') is eliminated, and the co-ordinates which we

use are generalized co-ordinates. The constraint force may be easily determined from

the second equation (6.2.36). If

, then the motion takes place as in the case in

which the surface is smooth; that motion is uniform if and only if

FfN

, hence if

and only if the tangential component of the given force equilibrates the force of sliding

friction.

2.2.4 Motion of a particle with a single degree of freedom in the conservative case

In the case of a particle (or of a mechanical system) with a single degree of freedom,

for which the equation of motion is of the form

()qfq

 ,

(6.2.37)

where

q is the generalized co-ordinate, we may set up a first integral of energy of the

form

()

[

]

2()qq UqUq−= −

() ()dUq fq q=

∫

(6.2.38)

by introducing the simple potential

U (or the scalar potential

U of a generalized

potential); hence, the corresponding mechanical system is a conservative system. As

well, one can show that a unidimensional conservative mechanical system (with a single

degree of freedom) or a pluridimensional one (if we succeed, by means of the first

integrals, to eliminate the corresponding parameters, obtaining a unidimensional one)

leads to an equation of motion of the form (6.2.37). We notice that this equation

corresponds to a non-linear free oscillation, without damping; the function

()

q is thus

a calling force. The equation (6.2.38) can be integrated in the form (6.2.18'), using the

notation

()

[

]

() 2 ()qq UqUqϕ =+ − .

(6.2.38')

One takes the sign + or – in (6.2.18') as the function

()qt is monotone increasing or

decreasing, respectively. It is necessary that

() 0qϕ ≥ , so that the motion be real.

Observing that

()

0qqϕ =≥ , we may assume that the function ()qt begins to

increase together with

t (corresponding to the direction of the initial velocity); the sign

+ is thus chosen. A study of the variation of the function

()qϕ and of its zeros leads to

interesting conclusions concerning the motion of the particle (or of the mechanical

system).

Noting

qp= , we may replace the equation (6.2.37) by the system

Dynamics of the particle with respect to an inertial frame of reference

399

()

= ,

(6.2.39)

which leads to

()

= ;

(6.2.39')

the motion of the particle is thus equivalent to the motion of a representative point

P in

the phase space of co-ordinates

,qp. The trajectory C in this space pierces the Oq -

axis by a right angle, and the tangent to it is parallel to this axis for

() 0

q = , 0p ≠ ;

if we have also

0p = , then one obtains a singular point, corresponding to a position of

equilibrium, as it results from the system (6.2.39).

Expressing the first integral (6.2.38) in the form

2()pVqh+=,

2( )hq Vq=+ , () ()Vq Uq

− ,

(6.2.40)

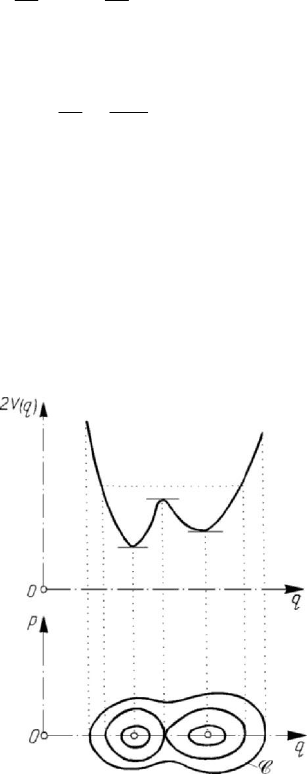
Figure 6.9. Motion of a particle with a single degree of freedom

in the conservative case.

where h is the energy constant, we notice that the trajectory C is symmetric with

respect to the

-axis and is situated in the domain 2()Vq h

≤

. On the basis of the

Lagrange-Dirichlet theorem (see Chap. 4, Subsec. 1.1.7), to the points of local

minimum of the potential energy

()Vq correspond stable positions of equilibrium,

while to the points of maximum correspond labile positions of equilibrium (Fig.6.9).

From the first equation (6.2.39), we see that – for

0p >

– q increases together with

the time

t , so that we may specify the direction of the trajectory. We obtain the period

of the motion in the form

MECHANICAL SYSTEMS, CLASSICAL MODELS

400

∫



(6.2.41)

integrating along a closed curve.

2.2.5 Study of a dissipative mechanical system with a single degree of freedom

If, during the motion, intervenes the friction too, then the mechanical energy is no

more conserved, but diminishes in time, due to the phenomenon of dissipation.

Assuming that the force of friction is a function of velocity, the equation of motion

becomes

() ()qfq Fq=+  , () 0qF q

≤

 ,

(6.2.42)

the last relation emphasizing that the damping force

()Fq is opposite to the velocity; in

fact, the equation (6.2.42) characterizes the damped non-linear free oscillations, in the

unidimensional case (with a single degree of freedom). In the case of forced

oscillations, this equation is completed in the form

() () ()qfq Fq t=++  F , () 0qF q

≤

 ,

(6.2.42')

where we have introduced also the perturbing force

()tF . In the case in which the

product

()qF q is positive for small values of the velocity modulus q and negative for

great values of the same modulus, one obtains self-sustained oscillations.

As in the case of undamped oscillations, the equation (6.2.42) leads to

() ( )

qFp

(6.2.43)

in the phase space, a field of vectors being thus defined, excepting the positions of

equilibrium (singular points). In the case in which the calling force

()

q is linear

(

()

qq= ) one can build up a polygonal line, which approximates the integral curve;

this procedure, due to Liénard, has been extended by J.L. Brown for the case in which

()

q is a non-linear function (the case of non-linear free oscillations).