Teodorescu P.P. Mechanical Systems, Classical Models Volume I: Particle Mechanics

Подождите немного. Документ загружается.

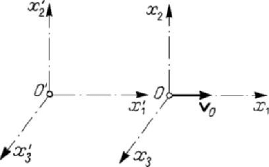
Dynamics of the particle with respect to an inertial frame of reference

371

xxvt

′′

=+,

′

;

(6.1.40')

Figure 6.3. Principle of relativity. The Galileo group.

it results that the set of these transformations contains only one essential parameter, that

is the magnitude

′

of the velocity of the frame R with respect to the frame

′

R . At

the moment

0t = (which can be taken as initial moment) the two frames coincide; we

notice that the inverse transformation

→

′

RR takes place too. As well, considering

also a frame

′′

and the transformation

→

′

′′

, of the form

′′ ′ ′ ′

=+rrv,

′′ ′

= , we observe that, by composition of the two transformations, we obtain the

transformation

→

′′

, of the form

′

′′′

+rrv, tt

′

, hence a transformation

of the same set of transformations, if we accept the law of composition of velocities of

the relative motion

000

′

′′

+vvv;

(6.1.41)

in the case of particular frames which have the properties of Fig.6.3, hence in the case

of the transformation (6.1.40'), the law of composition of velocities is

000

vvv

′

′′

+ .

(6.1.41')

It results that the set of transformations (6.1.40) forms a group, denoted by

Γ and

called the Galileo group; this group contains three parameters.

We may attach to this group the group of time translations, denoted by

T and

containing one parameter, specified by

ttt

′

+ ,

(6.1.42)

which leads to a change of initial moment (which becomes

), as well as the group of

space translations in

, denoted by

, containing three parameters and expressed in

the form

′

+rrr,

(6.1.42')

so that the two frames can no more coincide. Combining these transformations, we may

write

MECHANICAL SYSTEMS, CLASSICAL MODELS

372

′′′

=+ +rrv r,

ttt

′

+ .

(6.1.42'')

We obtain thus a transformation which forms a group with seven parameters; in such a

transformation, the axes of the right-handed orthonormed frames

R and

′

remain

parallel to themselves. We obtain a rotation of the frame

R with respect to the frame

′

by the transformation (see also Chap. 2, Subsec. 1.1.2)

′

=rrα

iijj

xxα

′

, 1, 2, 3i

(6.1.43)

which forms the group of proper (finite) rotations in

E , denoted by SO(3) (the special

orthogonal group in

E ); this group contains only three distinct constants (which –

eventually – may be Euler’s angles), because the tensor

verifies the six relations of

orthogonality (3.1.35).

Finally, starting from the transformations (6.1.40), (6.1.42), (6.1.42') and (6.1.43),

we may set up the transformation

′

=+ +rrvrα ,

ttt

′

+ ,

(6.1.44)

which forms a group with ten parameters, denoted by

G and called the Galileo-Newton

group; the groups

Γ , T, T and SO(3) are subgroups of the group G. In particular, for

= 1α we find again the transformation (6.1.42'').

1.2.4 General theorems

Starting from the equation of motion (6.1.22), written with respect to an inertial

frame of reference

R, considered fixed, we may state some theorems with a general

character, consequence of this equation, which are known as the general (universal)

theorems of the dynamics of the particle.

Taking into account the momentum (6.1.1) and that the mass

m of the particle is

constant, we may write the equation (6.1.22) in the form



, 1, 2, 3i

(6.1.45)

corresponding to the second law of mechanics, so as it was stated by Newton (see also,

Chap. 1, Subsec. 1.2.1); we may thus state

Theorem 6.1.7 (theorem of momentum). The derivative with respect to time of the

momentum of a free particle is equal to the resultant of the given forces which act upon

it.

This form of Newton’s second law is the same as that stated by Einstein in the

Special Theory of Relativity.

If we perform a left vector product of the relation (6.1.22) by

r and notice that

[]

() () () ()

mmmm

××+×=×





rvrvrvrr= ,

Dynamics of the particle with respect to an inertial frame of reference

373

introducing also the moment of momentum (6.1.2), then we may write

=×=



KrFM=

Oi Oi

KM=



, 1, 2, 3i

;

(6.1.46)

we obtain thus

Theorem 6.1.8 (theorem of moment of momentum). The derivative with respect to time

of the moment of momentum of a free particle with respect to a fixed pole is equal to the

moment of the resultant of the given forces which act upon it, with respect to the same

pole.

By means of the notion of hodograph, introduced in Chap. 5, Subsec. 1.2.1, we may

give a kinematic interpretation to the Theorems 6.1.7 and 6.1.8 too, stating:

Theorem 6.1.7'. The velocity of a point which describes the hodograph of the

momentum of a free particle with respect to a fixed pole is equipollent to the resultant

of the given forces which act upon it.

Theorem 6.1.8'. The velocity of a point which describes the hodograph of the moment

of momentum of a free particle with respect to a fixed pole is equipollent to the moment

of the given forces which act upon it, with respect to the same pole.

The torsor of the momentum, specified by the relation (6.1.4) allows to write

d()

() ()

τ= τ



(6.1.47)

where we took into account the formulae (6.1.45), (6.1.46); therefore, we state

Theorem 6.1.9 (torsor’s theorem). The derivative with respect to time of the torsor of

the momentum of a free particle with respect to a fixed pole is equal to the torsor of the

resultant of the given forces which act upon it, with respect to the same pole.

The relation (6.1.45) may be written also in the form

ddtHF

, (6.1.45')

wherefrom

() () d

tt tΔ−

∫

HH H F==;

(6.1.45'')

the variation of the momentum of a free particle in a finite interval of time is thus

emphasized. The quantity

∫

F represents the impulse of the given force,

corresponding to the interval of time

[

]

,tt .

As well, another form of the relation (6.1.46) is

tKM

, (6.1.46')

so that

() () d

OO O O

tt tΔ−

∫

KK K M==,

(6.1.46'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

374

and the variation of the moment of momentum of a free particle in a finite interval of

time is put into evidence; the quantity

∫

M represents the impulse of the moment

of the given force with respect to the pole

O , corresponding to the interval of time

[

]

,tt . Analogously, we get the variation of the torsor of the momentum of a free

particle in a finite interval of time in the form

(

)

() d

tΔτ = τ

∫

(6.1.47')

The above considerations play an important rôle in the case of an interval of time and

– particularly – in the case of discontinuous phenomena.

If we return to the kinetic energy

T , introduced in Subsec. 1.1.2, we may write the

relation

dd dTW

⋅Fr

; (6.1.48)

hence, we state

Theorem 6.1.10 (theorem of kinetic energy). The differential of the kinetic energy of a

free particle is equal to the elementary work of the resultant of the given forces which

act upon it.

Dividing the relation (6.1.48) by

dt and taking into account (6.1.16'), we can write

this theorem in a form closer to that of the previous theorems, i.e.



(6.1.48')

obtaining thus

Theorem 6.1.10' (theorem of kinetic energy; second form). The derivative with respect

to time of the kinetic energy of a free particle is equal to the power of the resultant of

the given forces which act upon it.

We notice that the elementary work is an exact differential only in the case of a

conservative force (which derives from a simple or a generalized potential). In general,

this work is not a total differential (it is a Pfaff form) and the theorem of kinetic energy

is written in the form (for

[

]

,ttt

∈

)



2121

() ()

TTt Tt T T WΔ= − = − =



12 1 1

ddd

PP t t

tPt=⋅=⋅=

∫∫∫

Fr Fv ,

(6.1.48'')

integrating between

P and

P ; we may thus state

Theorem 6.1.10'' (theorem of kinetic energy; finite form). The variation of the kinetic

energy of a free particle in a finite interval of time is equal to the work of the resultant

of the given forces which act upon it in that interval of time.

The scalar product of relation (6.1.45'') by

v leads to

Dynamics of the particle with respect to an inertial frame of reference

375

2122

mm t−⋅=⋅

∫

vvvvF;

introducing the notations

Tm=

v ,

Tm=

v ,

TT T

=−,

Tm=

v ,

−vvv,

(6.1.49)

we may write

TT tΔ+ = ⋅

∫

vF,

(6.1.50)

wherefrom we state

Theorem 6.1.11. The sum of the variation of the kinetic energy of a free particle in a

finite interval of time and the kinetic energy of the variation of the velocity in the same

interval of time is equal to the scalar product of the impulse of the resultant of the given

forces corresponding to the considered interval of time by the velocity of the particle at

the final moment.

The scalar product of the relation (6.1.45'') by

v leads – analogously – to

TT tΔ− = ⋅

∫

vF;

(6.1.50')

we thus state

Theorem 6.1.11'. The difference between the variation of the kinetic energy of a free

particle in a finite interval of time and the kinetic energy of the variation of the velocity

in the same interval of time is equal to the scalar product of the impulse of the resultant

of the given forces, corresponding to the considered interval of time, by the velocity of

the particle at the initial moment.

Summing the relations (6.1.50) and (6.1.50') and taking into account the relation

(6.1.48''), we get



()d

TW tΔ= = + ⋅

∫

vv F,

(6.1.51)

and we may state

Theorem 6.1.12 (Kelvin). The work of the resultant of the given forces which act upon

a free particle in a finite interval of time (the variation of the kinetic energy of the

particle) is equal to the scalar product of the impulse of this resultant, corresponding to

the considered interval of time, by the semisum of the velocities of the particle at the

initial and the final moment.

Subtracting the relations (6.1.50) and (6.1.50') one of the other, we may write

Tt=⋅

∫

vF;

(6.1.51')

MECHANICAL SYSTEMS, CLASSICAL MODELS

376

we get

Theorem 6.1.12' (analogous of Kelvin’s theorem). The kinetic energy of the variation

of the velocity of a free particle in a finite interval of time is equal to half of the scalar

product of the impulse of the resultant of the given forces, corresponding to the

considered interval of time, by the variation of the velocity in the same interval of time.

Figure 6.4. General theorems with respect to a movable pole.

The general theorems stated above take place in an inertial frame of reference

considered fixed; the theorems of moment of momentum and of torsor, which depend

on the pole

, maintain their form also with respect to another pole Q , rigidly linked

to the frame

R (fixed with respect to this frame). If the pole Q is movable and the

calculation is made with respect to the frame

R too, the momentum

remains

invariant, but the moment of momentum and the moment of the resultant of given

forces become (Fig.6.4)

()

OQ QQ

=× = + × = + ×



KrHrrHKrH

OQQ

+×MMrF;

in this case, replacing in relation (6.1.46) and taking into account the relation (6.1.45),

we may write

QQQ

==−×



KMvH

(6.1.52)

obtaining thus a generalized form of the theorem of moment of momentum. As a

consequence, the formula (6.1.47) is generalized in the form

{}

d()

() () ,

QQQ

τ= =τ− ×



HF0vH

(6.1.52')

1.2.5 Conservation theorems

If the resultant F of the given forces which act upon the particle P fulfils certain

conditions, then the general theorems presented in the previous subsection allow to state

some conservation theorems. Thus, if the force

F is parallel to a fixed plane (is normal

to a fixed direction of unit vector

u with respect to the frame R or has a zero

component), then the theorem of momentum allows to write

Dynamics of the particle with respect to an inertial frame of reference

377

d( )

⋅

⋅= ⋅+ ⋅= =⋅=





Hu Hu Hu Fu

wherefrom

()

ii ii

mHumvuC⋅= ⋅= = =Hu v u , constC

;

(6.1.53)

we obtain thus a scalar first integral of the equations of motion. Hence, if the force

F is

parallel to a fixed plane, then the projection of the velocity of the free particle

P on the

normal to this plane is conserved (is constant) in time; associating a particle

′

to the

projection of the particle

P on this normal, we may state that the particle P

′

has a

uniform motion. Because

() () ( )

mmm C

⋅

=⋅= ⋅=



vu ru ru ,

it results

()

mmxuCtC

′

⋅= = +ru , ,constCC

′

(6.1.53')

being thus led to a new scalar first integral, independent of the previous one; the

mentioned condition allows us to set up two independent scalar first integrals. As well,

if the force

F has a fixed direction (is normal to two distinct fixed directions with

respect to the frame

R or has two zero components), then one obtains four

independent scalar first integrals of the form (6.1.53), (6.1.53'), while the projection of

the velocity of the particle on a plane normal to the given force (determined by the two

fixed directions) is conserved in time. Eliminating the time between the two first

integrals of the form (6.1.53'), we may state that – in this case – the trajectory of the

particle

P is a plane curve, the support of the force F being contained in the plane of

the curve too. We may start also from the equation of motion

()mFt



ru, vers const==





uF ,

wherefrom one obtains the vector

d()dmtFttt

′

−= +

∫∫

rC u C, ,const

′





CC ,

as a linear combination of the constant vectors

and C , hence it is contained in the

plane defined by these vectors. Associating a particle

′

to the projection of the

particle

P on a normal to the direction of the force F in the considered plane, we

notice that this particle has a uniform and rectilinear motion.

Finally, if the force

F vanishes (is normal to three distinct fixed directions), then we

may build up three independent scalar first integrals of the form (6.1.53). Besides,

=F0 leads to =



, so that

m==HvC, const=





C ,

, 1, 2, 3i

;

(6.1.53'')

MECHANICAL SYSTEMS, CLASSICAL MODELS

378

hence we get a vector first integral, equivalent to three independent scalar first integrals.

We may state

Theorem 6.1.13 (conservation theorem of momentum). The momentum (and the

velocity) of a free particle is conserved in time if and only if the resultant of the given

forces which act upon it vanishes.

We notice that the relation



vrC leads to

′

=+rC C,

,const

′





ii i

mx C t C

′

+ ,

1, 2, 3i

;

(6.1.53''')

we obtain thus a new vector first integral, equivalent to three scalar first integrals. The

conservation theorem of momentum allows to set up two independent vector first

integrals or six independent scalar first integrals (the maximal number of independent

scalar first integrals which can be obtained). The motion of the particle

P is thus

rectilinear and uniform, being completely determined with respect to the frame

Besides, this result corresponds to the principle of inertia, which appears thus as a

particular case of the principle of action of forces; however, this principle preserves its

independence, because it is not necessary to introduce the notion of zero resultant

(

=F0), as well as because it can lead to a selection of the solution of the problem

with initial conditions (of Cauchy type) if not all the conditions asked by the sufficient

theorem of existence and uniqueness are fulfilled. As it was seen above, this principle is

not in contradiction with the other principles. We notice also that this principle

maintains its form in relativistic mechanics, even if it cannot be deduced by

particularizing.

Analogously, if the moment

is contained in a fixed plane (is normal to a fixed

axis

Δ , O Δ∈ , of unit vector u , with respect to a frame R, or has a vanishing

component), the theorem of moment of momentum leads to

() 0

OOO

⋅

=⋅=⋅=



Ku Ku Mu ,

so that

(, , )

iij

OOiijkk

mKumxvuC⋅= = =∈ =Ku rvu , constC

(6.1.54)

resulting thus a new scalar first integral of the equations of motion. The mentioned

condition holds if and only if the force

F is coplanar (concurrent or parallel) with the

axis

Δ ( 0M

= ); in this case, the projection of the moment of momentum

K on the

axis

Δ is conserved in time. If, in particular, the axis Δ coincides with the axis

Ox ,

we have

()( )

12 21 12 21

mxv xv mxx xx C−= −= , constC

(6.1.54')

As well, if the moment

M has a fixed support (is normal to two distinct fixed axes

Δ and

Δ with respect to the frame R or has two zero components), then we obtain

Dynamics of the particle with respect to an inertial frame of reference

379

two independent scalar first integrals of the form (6.1.54). This condition holds if and

only if the force

F is contained in a fixed plane Π (normal to the direction of the

moment

M and passing through

O ΔΔ

≡

∩ ) or the support of the force F passes

through the point

O . Indeed, if the axes

Δ and

Δ coincide with the axes

Ox and

Ox , respectively, the relations

23 32

MxFxF≡−=

31 13

MxFxF

≡

−=

lead to

(

)

12 312213

12 3

OO O

xM xM x xF xF xM+=− −=−=;

hence, we may have

0x = or

In the first case, the field of forces

F being coplanar, the trajectory of the particle P

is a plane curve contained in the plane

Π , while the moment of momentum

K is

normal to this plane. In the second case,

M0 (the moment

M is normal to three

distinct axes, so that we may set up three independent first integrals of the form

(6.1.54). Besides,

=M0 leads to

K0, so that

()

m=× =Kr vC, const=





C ,

Oi ijk k

KmxvC=∈ = , 1, 2, 3i

, (6.1.54'')

hence a vector first integral, equivalent to three scalar first integrals; we may state

Theorem 6.1.14 (conservation theorem of moment of momentum). The moment of

momentum of a free particle with respect to a fixed pole is conserved in time if and only

if the moment of the resultant of the given forces which act upon it, with respect to the

same pole, vanishes.

We notice that the conservation theorem of momentum entails the conservation

theorem of moment of momentum; hence, the vector first integral or the three

corresponding scalar first integrals, given by the moment of momentum conservation

theorem, are not independent of the six scalar first integrals given by the momentum

conservation theorem. In this case, we may write

() const

τ=





(6.1.54''')

and we may state

Theorem 6.1.15 (conservation theorem of torsor). The torsor of the momentum of a

free particle with respect to a fixed pole is conserved in time if and only if the resultant

of the given forces which act upon it vanishes.

Considering only the vector first integrals (6.1.53'') and (6.1.54''), which form the

first integral of the torsor (6.1.54'''), one obtains six scalar first integrals (we do not take

into account the vector first integral (6.1.53''')), which are not independent, being linked

by the relation

0⋅=CC (consequence of the relation (,, )0

⋅

==HK vr v ).

MECHANICAL SYSTEMS, CLASSICAL MODELS

380

We notice that, in the frame of the Theorem 6.1.15, the torsor of the force

vanishes too. As a matter of fact, the torsor conservation theorem allows to write nine

scalar first integrals, from which only six are independent.

If the force

F is contained in the fixed plane

Ox x , then we have

0F = ,

MM== and we may build up four first integrals

13 3

vC≡=,

233 3

xCtC

′

≡

−=,

32332

fxvxv

≡−=

43113

fxvxv

≡−=

3312

,,, constCCCC

′

which are independent, because the matrix

()

1234

32 32

123123

313 1

00000 1

00100 0

,,,

,,,,,

ffff

vv xx

xxxvvv

vvx x

⎡

⎤

⎢

⎥

∂

⎢

⎥

⎡⎤

⎢

⎥

⎢⎥

−−

∂

⎣⎦

⎢

⎥

⎢

⎥

−−

⎣

⎦

is of rank four (e.g., the determinant of the fourth order formed by the last four columns

does not vanish). If we put the initial conditions in the plane

Ox x , then we notice that

0CC

′

==; the other first integrals lead to

0CC

= . The co-ordinates

()xxt= and

()xxt= and the components of the velocity

()vvt= ,

()vvt= remain to be determinate. Thus, the theorems of linear and angular

momentum may give independent first integrals; but such a result cannot be obtained

always. Thus, if the force

F is parallel to the fixed axis

Ox (without having –

necessarily – a fixed support), then we have

0FF

= ,

and we may set

up five first integrals

11 1

vC≡=,

211 1

xCtC

′

≡− =,

32 2

≡

= ,

422 2

xCtC

′

≡

−=,

12 21

fxvxv

≡−=

11223

,,,, constCCCCC

′′

= ;

one may easily see that the last first integral is a consequence of the four first integrals,

having only four independent first integrals.

Using the considerations made in Subsec. 1.1.2, let us suppose that the resultant

of the given forces is a conservative force which derives from a simple or generalized

potential; in this case, the elementary work is a total differential and the formula

(6.1.48) leads to

TUh

(6.1.55)

or to

TU h

+ , (6.1.55')