Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.

Рекомендуемая литература
41
γ —
k
P
l=1
(k
l
+ n
l
) -вектор-столбец параметров регрессии;
η — k(n + 1) -вектор-столбец остатков по наблюдениям.
Легко проверить, чт о матрица ковариации остатков η удовле-
творяе т следующему соотношению:
E(ηη
′
) = σ
2
Ω ⊗ (Z
′
Z).
Для нее имеется оценка: k(n+1)×(n+1) -матрица Σ = W ⊗(Z
′
Z).
Эта матрица отлична от σ
2
I
k(n+1)
, поэтому на третьем шаге 3М-
оценивания к единой системе (1.31) применяется ОМНК и получа-
ется окончательная оценка c параметров γ :
c = (Q
′
Σ
−1
Q)
−1
Q
′
Σ
−1
Y.
Рекомендуемая литература
1. Айвазян С.А. Основы эконометрики. Т. 2. — М.: Юнити,
2001. (Гл. 4.)
2. Бриллинджер Д. Временные ряды. Обработка данных и тео-
рия. — М.: Мир, 1980. (Гл. 10.)
42
Глава 1. Системы регрессионных уравнений
3. Джонстон Дж. Эконометрические мет оды. — М.: Статисти-
ка, 1980. (Гл. 12.)
4. Доугерт и К. Введение в эконометрику. — М.: Инфра-М,
1997. (Гл. 11.)
5. Кейн Э. Э кономическая статистика и эконометрия. Вып. 2 . —
М.: Статистика, 1977. (Гл. 13.)
6. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Экономет-
рика — начальный курс. — М.: Дело, 2000. (Гл. 10.)
7. (*) Маленво Э . Статистические методы эконометрии. Вып.
2. — М.: Статистика, 1975. (Гл. 17–20.)
8. Ти нт ер Г. Введение в эконометрию. — М.: Статистика, 1965.
(Гл. 6.)
9. Badi H.B. Ec onometrics. — 2nd edition. — Springer, 1999. (Ch.
11.)
10. Russel D., James G.M. Estimation and Inference in Econo-
metrics. — Oxford University Press, 1993. (Ch. 7, 18.)

Рекомендуемая литература
43
11. Greene W.H. Econometric Analysis. — Prentice-Hall, 2000. (Ch. 15,
16.)
12. Judge G.G., Hill R.C., Griffiths W.E., Lu
tkepohl H., Lee
T. Introduction to the Theory and Practice of Econometric. —
John Wiley & Sons, 1993. (Ch. 14, 15.)
13. Maddala G.S. Introduction to Econometrics. — 2nd ed. —
Prentice Hall, 1992. (Ch. 9.)
14. Ruud Paul A. An Introduction to Classical Econometric
Theory. — Oxford University Press, 2000. (Ch. 26.)
15. Griffiths W.E., Hill R.C., Judge G.G. Learning and Practicing
econometrics. — John Wiley & Sons, 1993. (Ch. 17.)
Глава 2.
Динамические
регрессионные модели
В экономике практически нет примеров мгновенного реагиро-
вания на какое-либо экономическое воздейс твие — сущес твуют за-
держк и прояв ления эффектов от капиталовложений, внесения удоб-
рений и т.д., поэтому при моделировании экономических процес-
сов необходимо учитывать воздействие фак торов в предыдущие
моменты времени.
44

2.1. Модель распределенного лага
45
2.1. Модель распределенного лага
Простейшая модель распределенного лага — это модель регрес-
сии, в которой на динамику исследуемой переменной x
t
влияет не
только к акой -то объясняющий фактор z
t
, но и его лаги. Модель
имеет следующий вид:
x
t
= µ +
q
X
j=0
α
j
z
t−j
+ ε
t
= µ + α(L)z
t
+ ε
t
, (2.1)
где α(L) =
q
P
j=0
α
j
L
j
, a q — величина максимального лага.
Данную модель можно охарактеризовать следующими показа-
телями.
Функция реакции на импульсы (impulse response function,
IRF) показывает, насколько изменится x
t
при изменении z
t−j
на
единицу для лагов j = 0, 1, 2, .... Таким образом, можно считать,
что речь идет о производной
dx
t
dz
t−j
как функции запаздывания j.
Ясно, что для модели распределенного лага этот показатель совпа-
дает с коэффициентом α
j
при j 6 q и равен нулю при j > q. При
j < 0 (влияние будущих значений переменной z на переменную
x) р еакцию на импульсы можно положить равной нулю.

46
Глава 2. Динамические регрессионные модели
Накопленная реакция на импульсы для лага k — это про-
суммированные значения простой функции реакции на импульсы
от j = 0 до j = k. Для модели распределенного лага это сумма
коэффициентов:
min{k, q}
X
j=0
α
j
.
Долгосрочный мультипликатор является измерителем обще-
го влияния переменной z на переменную x. Он равен
α
Σ
=
q
X
j=0
α
j
= α(1).
Это предельное значение накопленной реакции на импульсы.
Если x и z — логарифмы исходных переменных, то α
Σ
— долго-
срочная эластичность.
Средняя длина лага показывает, на сколько периодов в сред-
нем запаздывает влияние переменной z на переменную x. Она
вычисляется по формуле
¯
j =
q
P
j=0
jα
j
q
P
j=0
α
j
=
q
P
j=0
jα
j
α
Σ
.
В случае мультиколлинеарности лаговых переменных обычно
на лаговую структуру накладывают какое-нибудь ограничение, что-

2.1. Модель распределенного лага
47
бы уменьшить количество оцениваемых коэффициентов. Рассмот-
рим две наиболее важные модели этого типа.
Полиномиальный лаг
Одна из возможных структур лага — полиномиальный лаг, ве-
са которого задаются многочленом от величины лага j:
α
j
=
p
X
s=0
γ
s
j
s
, j = 0, . . . , q, (2.2)
где p — степень многочлена, p < q. Эту модель предложила С.
Алмон, поэтому часто используют термин «лаг А лмон» (Almon
lag).
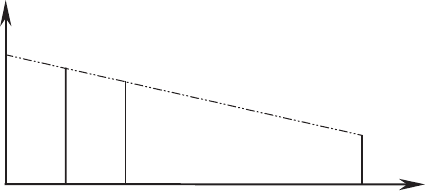
Простейший полиномиальный лаг — линей н ый. Д ля него α
j
=
γ
0
+ γ
1
j. Как правило, здесь γ
1
< 0. Его структура изображена на
диаграмме (рис. 2.1).
C учетом выражений для α
j
, проведем преобразование исход-
ной модели:
q
X
j=0
α
j
z
t−j
=
q
X
j=0
p
X
s=0
γ
s
j
s
!
|
{z }
α
j
z
t−j
=
p
X
s=0
γ
s
q
X
j=0
j
s
z
t−j
=
p
X
s=0
γ
s
y
ts
.
48
Глава 2. Динамические регрессионные модели
α
j
0
1
2
q
j
. . . . .
Рис. 2.1
Получим новую модель линейной регрессии:
x
t
= µ +
p
X
s=0
γ
s
y
ts
+ ε
t
с преобразованными факторами
y
ts
=
q
X
j=0
j
s
z
t−j
.
Оценив γ
s
, можно вычислить веса α
j
, воспользовавшись ф ор-
мулой (2.2).
Геометрический лаг
Веса геометрического лага α
j
задаются следующими соотно-
шениями:
α
j
= α
0
δ
j
, j = 0, . . . , ∞,

2.1. Модель распределенного лага
49
α
j
0
1
2
j
. . . .
3
Рис. 2.2
где 0 < δ < 1. Веса геометрического лага убывают экспоненциаль-
но с увеличением лага (рис. 2 .2).
Модель распределенного лага с этими весами, модель Койка,
имеет следующий вид:
x
t
= µ + α
0
∞
X
j=0
δ
j
z
t−j
+ ε
t
. (2.3)
Выражение упрощается с использованием формулы суммы бес-
конечной геометрической прогре ссии:
x
t
= µ + α
0
1
1 − δL
z
t
+ ε
t
.
В ре зультате имеем модель, полученную в результате преобразо-
вания Койка:
x
t
= µ
′
+ δx
t−1
+ α
0
z
t
+ ε
′
t
,
50
Глава 2. Динамические регрессионные модели
где µ
′
= (1 − δ)µ и ε
′
t
= ε
t
− δε
t−1
.
В полученной модели ошибка ε
′
t
не является белым шумом,
а представляе т собой процесс скользящего среднего первого поряд-
ка. Модель является линейной ре грессией, однако для нее не вы-
полнено т ребование о некоррелированности регрессоров и ошибки.
Действительно, ε
t−1
входит как в x
t−1
, так и в ε
′
t
. Следовательно,
оценки метода наименьших квадратов не являются состоятельны-
ми и следует пользоваться другими методами.
Можно оценивать модель Койка в исходном виде (2.3). Сумму
в этом уравнении можно разделить на две части: соответ ствую-
щую имеющи мся наблюдениям для переменной z
t
и относящуюся
к прошлым ненаблюдаемым значениям, т.е. z
0
, z
−1
и т.д.:
x
t
= µ + α
0
t−1
X
j=0
δ
j
z
t−j
+ α
0
∞
X
j=t
δ
j
z
t−j
+ ε
t
.
Далее, во второй сумме сделаем замену j = s + t:
x
t
= µ + α
0
t−1
X
j=0
δ
j
z
t−j
+ α
0
δ
t
∞
X
s=0
δ
s
z
−s
+ ε
t
.
