Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.

1.2. Взаимозависимые или одновременные уравнения
21
x
p
s
d
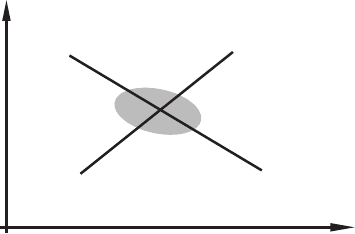
Рис. 1.1
только цена, и линии спроса и предложения в плоскост и , абсцис-
сой которой является цена, не меняют своего положения. Поэтому
наблюдаемые пары (p, x) сконцентрированы вокруг единственной
точки равновесия, облако наблюдений не имеет вытянутостей, и
зависимости x от p статистически выявить невозможно (рис. 1.1).
Статистически оба уравнения одинаковы, и нет оснований счи-
тать коэффициент регрессии, например, x по p , эластичностью
спроса и ли предложения по цене. Более того, в данном случае эта
регрессия будет не значима. Эти уравнения не идентифицированы.
Действительно, k = 2 , n = 0, r
1
= r
2
= 0 и необходимое условие
идентификации (1.12) для обоих уравнений не выполнено.
22
Глава 1. Системы регрессионных уравнений
Пусть речь идет о товаре, имеющем сельскохозяйственное про-
исхождение. Тогда его предложение зависит от погодных условий,
и в модель следует ввести переменную z
1
— некий индекс погоды
в течение сельскохозяйственного цикла. В правую часть соотно-
шения (1.15) вводится дополнительное слагаемое:
z
1
[ a
11
0 ] . (1.16)
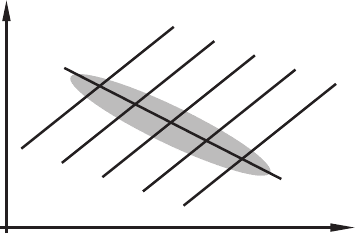
Если модель (1.15, 1.16) истинна (гипотеза g3), то подвижной
станови тся линия предложения (погодные условия в разные сель-
скохозяйственные циклы различны), и облако фактических наблю-
дений вытягивается вдоль линии спроса. Регре ссия x на p да-
ет оценку эласти чности спроса по цене (рис. 1.2). В этой ситуа-
ции уравнение предложения по-прежнему не идентифицировано,
x
p
s
1
s
2
s
3
s
4
s
5
d
Рис. 1.2
1.2. Взаимозависимые или одновременные уравнения
23
но для уравнения спроса условия идентификации (1.12 ) выполне-
ны, и это уравнение идентифицировано.
Действительно: k = 2, n = 1, r
1
= 0, r
2
= 1 и r
1
< k − 1, r
2
=
k − 1 . Боле е убедительно этот результат можно получить, исполь-
зуя необходимые и достаточные условия идентификации (1.13).
Матрица H в этих условиях имеет следующий вид:
H =
1 1
−b
21
b
22
−a
11
0
c
1
c
2
.
Матрица R
1
— пустая ( r
l
= 0 ), и условия (1. 13) для пер-
вого уравнения не выполняются. Для второго уравнения R
2
=
[0 0 1 0], и матрица R
2
H равна [−a
11
0] , т.е. ее ранг равен еди-
нице, и условие (1.13) выполнено. А матрица, составленная из ко-
эффициентов во всех прочих уравнениях, кроме второго, при пе-

24
Глава 1. Системы регрессионных уравнений
x
p
s
d
1
d
2
d
3
d
4
d
5
d
6
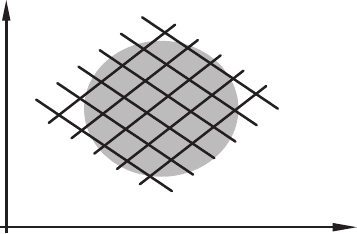
Рис. 1.3
ременных, которые исключены из второго уравнения, есть [−a
11
] ,
т.е. она не вырождена.
Теперь рассматривается другая возможность: изучаемый товар
входит в потре бительскую корзину, и спрос на него зависит от
доходов домашних хозяйс тв. В модель в водится переменная z
2
до-
ходов домашних хозяйств, т.е. в правую часть соотношений (1.15)
добавляется слагаемое
z
2
[ 0 a
22
] . (1.1 7 )
Если истинна модель (1.15, 1.17), то подвижной окажется ли-
ния спроса (разные домашние хозяйства и меют разные доходы),
и регрессия x на p даст оценку э ластичности предложения по
цене (рис. 1.3). В такой ситуации не идентифицировано уравнение
1.2. Взаимозависимые или одновременные уравнения
25
спроса. Уравнение предложения идентифицировано: k = 2, n = 1,
r
1
= 1, r
2
= 0 и r
1
= k − 1, r
2
< k − 1 .
Понятно, что можно говорить о модели, в которую входят обе
отмеченные переменные: и z
1
и z
2
. Это — модель (1.15, 1. 1 6, 1.17).
В правую часть (1.15) добавляется слагаемое
[z
1
z
2
]
a
11
0
0 a
22
.
В эт ом случае идентифицированы оба уравнения: k = 2, n = 1 ,
r
1
= r
2
= 1 = k − 1. Но поскольку подвижны обе линии — и спро-
са, и предложения — облако наблюдений не имеет вытянутост ей
(рис. 1.4), и регрессия x на p опять оказывается не значимой .
Для оценки параметров регрессии требуется использовать специ-
альные методы, рассматриваемые ниже . Впрочем, и в двух преды-
дущих случаях необходимо использование специальных методов
оценки параметров взаимозависимых систем, т.к. обычный МНК
дает смещенные и несостоятельные оценки.
26
Глава 1. Системы регрессионных уравнений
x
p
d
1
d
2
d
3
d
4
d
5
d
6
s
2
s
1
s
3
s
4
s
5
Рис. 1.4
Пусть теперь на предложение товара влияет еще один фактор
z
3
, показывающий, например, количество удобрений на единицу
площади, с которой собирается продукт, при нимающий в дальней-
шем форму товара. Тогда в правой части уравнения (1.15) возни-
кает слагаемое
[z
1
z
3
]
a
11
0
a
13
0
,
и первое уравнение по-прежнему остается не идентифицирован-
ным, а второе оказывается сверхидентифицированным.
Далее ряд утверждений будет иллюстрироваться на примере
модели (1.1 5, 1.1 6). В иллюстрациях эту модель удобнее записывать

1.2. Взаимозависимые или одновременные уравнения
27
в сокращенном виде:
[ ˆx ˆp ]
1 1
−β
21
β
22
= ˆz
1
[ α
11
0 ] + [ ε
1
ε
2
] . (1.18)
Поскольку
1 1
−β
21
β
22
−1
=
1
β
21
+ β
22
β
22
−1
β
21
1
,
приведенная форма модели имеет следующий вид:
[ ˆx ˆp ] = ˆz
1
[ d
11
d
12
] + [ η
1
η
2
] =
=
1
β
21
+ β
22
(ˆz
1
[ α
11
β
22
− α
11
] + [ ε
1
β
22
+ ε
2
β
21
ε
2
− ε
1
]). (1.19)
Из этого соотношения видно, как d и η связаны с β и ε .
Дальнейшее изложение ведется в предположении, что с троки
матрицы R
l
— орты.
28
Глава 1. Системы регрессионных уравнений
1.3. Оценка параметров отдельного урав-
нения
Вводятся дополнительные обозначения:
X
l
— N ×k
l
-матрица наблюдений за изучаемыми переменными
x
l
, входящими в l -е уравнение;
X
l
— N -вектор-столбец наблюдений за l -й переменной x
l
;
X
l
−
— N × (k
l
− 1) -матрица X
l
без ст олбца X
l
наблюдений
за x
l
;
β
l
— k
l
-вектор-столбец параметров при изучаемых перемен-
ных в l -м уравнении;
β
l
— (k
l
− 1) -вектор-столбец β
l
с обратным знаком и без l -го
элемента β
ll
= 1 ;
Z
l
— N ×(n
l
+1) -матрица наблюдений за независимыми факт о-
рами z
l
, входящими в l -е уравнение, включая единичный столбец,
соответствующий свободному члену;
1.3. Оценка параметров отдельного уравнения
29
α
l
— (n
l
+ 1) -вектор-столбец параметров при этих факторах
вместе со свободным членом;
ε
l
— N - вектор-столбец остатков в l -м уравнении по наблюде-
ниям.
Тогда l -е уравнение регрессии можно записать следующим об -
разом:
X
l
β
l
= Z
l
α
l
+ ε
l
(1.20)
или
X
l
= X
l
−
β
l
+ Z
l
α
l
+ ε
l
. (1.21)
Применение обычного МНК к этому уравнению дает в общем слу-
чае смещенные и несостоятельные оценки, прежде всего потому,
что остатки ε
l
скорее всего коррелированы с регрессорами X
l
, ко-
торые к тому же недетерминированы и наблюдаются с ошибками
(гипотеза g2 нарушена).
Для иллюстрации справедливости этого утверждения исполь-
зуется модель (1.15, 1.16). Пусть эта модель истинна, и тогда ре-
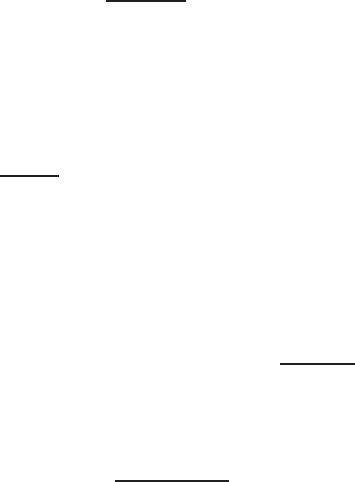
30
Глава 1. Системы регрессионных уравнений
грессия x на p даст оценку −β
22
:
−b
мнк
22
=
P
ˆx
i
ˆp
i
P
ˆp
2
i
. (1.22)
Это выражение можно преобразовать, используя (1.18, 1.1 9) (чтобы
не загромождать записи,
1
P
ˆp
2
i
обозначено через P ):
− b
мнк
22
= P
X
ˆx
i
ˆp
i
ˆx
i
=−β
22
ˆp
i
+ε
i2
= −β
22
+ P
X
ε
i2
ˆp
i
ˆp
i
=ˆz
i1
d
12
+η
i2
=
= −β
22
+ P
d
12
X
ˆz
i1
ε
i2
+
X
η
i2
ε
i2
η
i2
=
ε
i2
−ε
i1
β
21
+β
22
= −β
22
+
+ P
d
12
X
ˆz
i1
ε
i2
+
1
β
21
+ β
22
X
ε
2
i2
−
X
ε
i1
ε
i2
!
.
Очевидно, что −b
мнк
22
по математическому ожиданию никак не
может равняться −β
22
, поскольку в правой части полученного вы-
ражения имеется
P
ε
2
i2
, т.е. дисперсия (в математическом ожида-
нии) остатка в уравнении по спросу, которая не равна нулю и к
тому же не будет уменьшаться с ростом N . Эта оценка смещена
и несостоятельна.
Если данное уравнение т очно идентифицировано, то для оцен-
ки его параметров можно использовать косвенный метод (КМ)
наименьших квадратов: с помощью МНК оцениваются парамет ры
