Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.

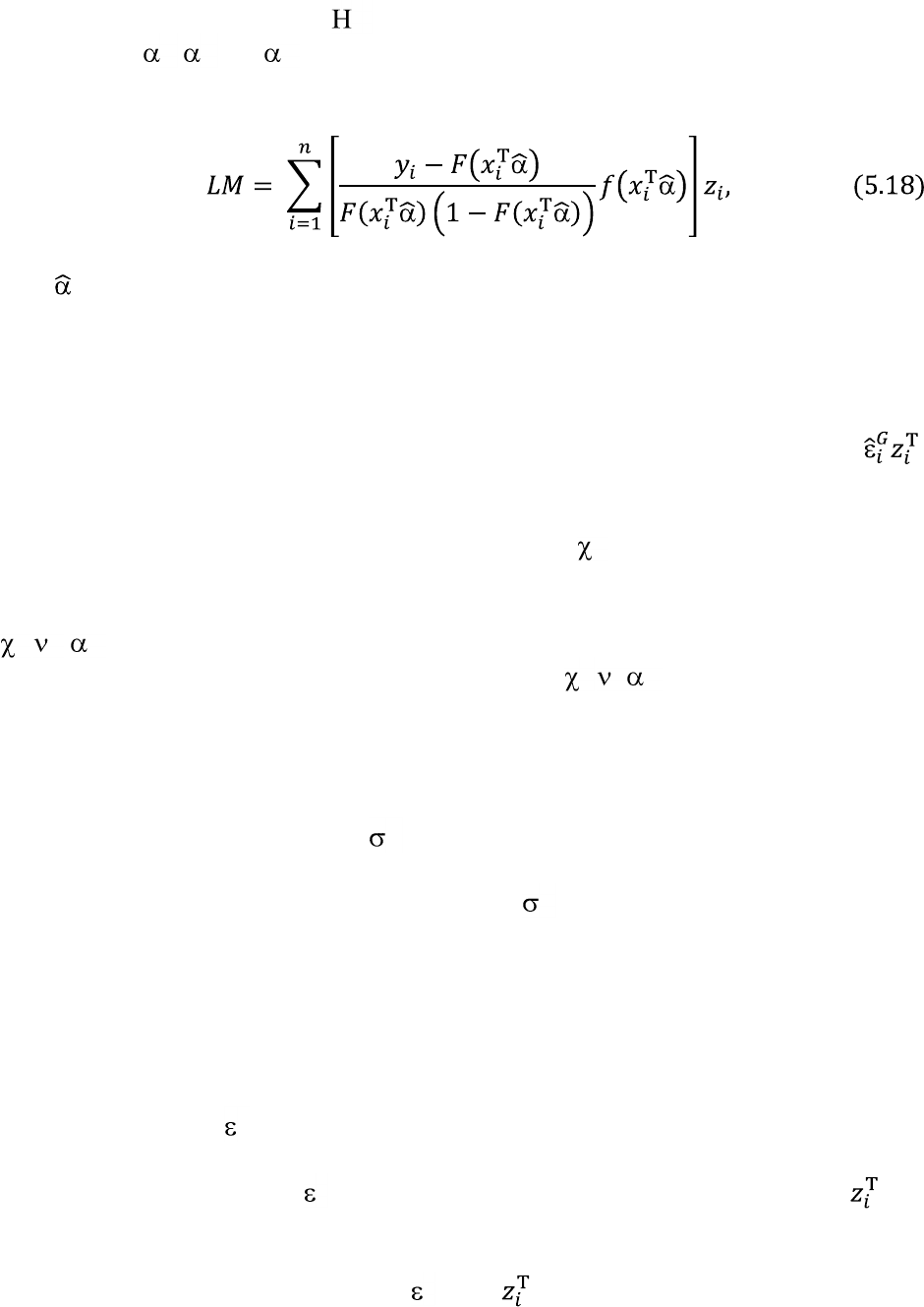
18
Альтернативная гипотеза
1
, напротив, говорит, что хотя бы один из
параметров
1
,
2
, …,
l
не равен нулю.
Для проверки гипотезы мы рассчитываем LM статистику в виде
где оценки регрессии с ограничениями на параметры, и проверяем,
существенно ли отличается LM статистика от нуля при условии, что в модели
отсутствуют l переменных.
Внимательное рассмотрение показывает, что выражение (5.18)
представляет собой ни больше, ни меньше, как коэффициент корреляции
пропущенных переменных модели z
i
= (z
i1
, z
i2
, …, z
il
)
T
с возмущениями: .
Если нулевая гипотеза об отсутствии значимого влияния пропущенных
переменных на распределение зависимой переменной справедлива, то
статистика критерия имеет асимптотическое
2
распределение с числом
степеней свободы, равным l, и, следовательно, избыточные переменные z
i1
, z
i2
,
…, z
il
могут войти в модель только с нулевыми коэффициентами. При LM <
2
( , ) у нас нет оснований отвергать нулевую гипотезу об отсутствии
влияния пропущенных переменных; при LM >
2
( , ) статистика попадает в
критическую область, следовательно, хотя бы одна из пропущенных
переменных оказывает существенное влияние, и еѐ необходимо включить в
модель.
Гетероскедастичность остатков. Гетероскедастичность остатков
выражаться в том, что var(e
i
) =
2
i
. Нулевая гипотеза о том, что
H
0
: var(e
i
) =
2
может быть протестирована с помощью логарифмической функции
наибольшего правдоподобия следующим образом.
Вначале сделаем предположение о форме зависимости дисперсии
возмущений. Предположим, что существует несколько экзогенных
переменных z
i
, которые оказывают влияние на разброс возмущений модели.
Пусть дисперсия
i
зависит от l экзогенных переменных z
i
, зависимость
выразим в виде некоторой положительной функции. Будем предполагать, что
функции дисперсии var (
i
) зависит от формы исследуемой модели g( β) –
логит, или пробит, в следующем виде:
var(
i
) = kg( β),

19
где k – константа, значение которой определяют в зависити от вида функции
g( β), так для пробит модели k = 1, а для логит модели константа
соответственно равна k =
2
/3, β – вектор паметров. Кроме того, избранная
функции дисперсии гарантирует нам, что
g > 0, g(0) = 1, g (0) = 1.
Подстановка указанной функции дисперсии в логарифмическую функцию
наибольшего правдоподобия позволяет получить выражение следующего
вида, которое зависит не только от , но и от β:
(5.19)
Если гетероскедастичность отсутствует, то есть var(e
i
) =
2
, тогда все
параметры в векторе β равны нулю. Поэтому гипотезу об отсутствии
гетероскедастичности мы вправе формулировать как гипотезу о равенстве
нулю всех параметров в векторе β. Поэтому при предположении, что верна
нулевая гипотеза
0
: β = 0 (5.20)
производная от (5.19) по β будет равна следующему выражению:
Выражение (5.21) представляет собой ни то иное как нецентрированный
коэффициент детерминации регрессии единиц на и .
Отметим следующие важные моменты в оценке критерия:
(1) приведѐнный в (5.21) критерий R
2
на гетероскедастичность не зависит от
формы функции g, а только от набора переменных z
i
, определяющих
интенсивость гетероскедастичности остатков;
(2) проведение нормализации в моделях бинарного выбора позволяет не
включать константу в состав z
i
;
(3) по определению условия первого порядка выражение = 0.
Если нулевая гипотеза об отсутствии гетероскедастиности вида var(
i
) =
kg( β) верно, то статистика, представленная коэффициентом детерминации
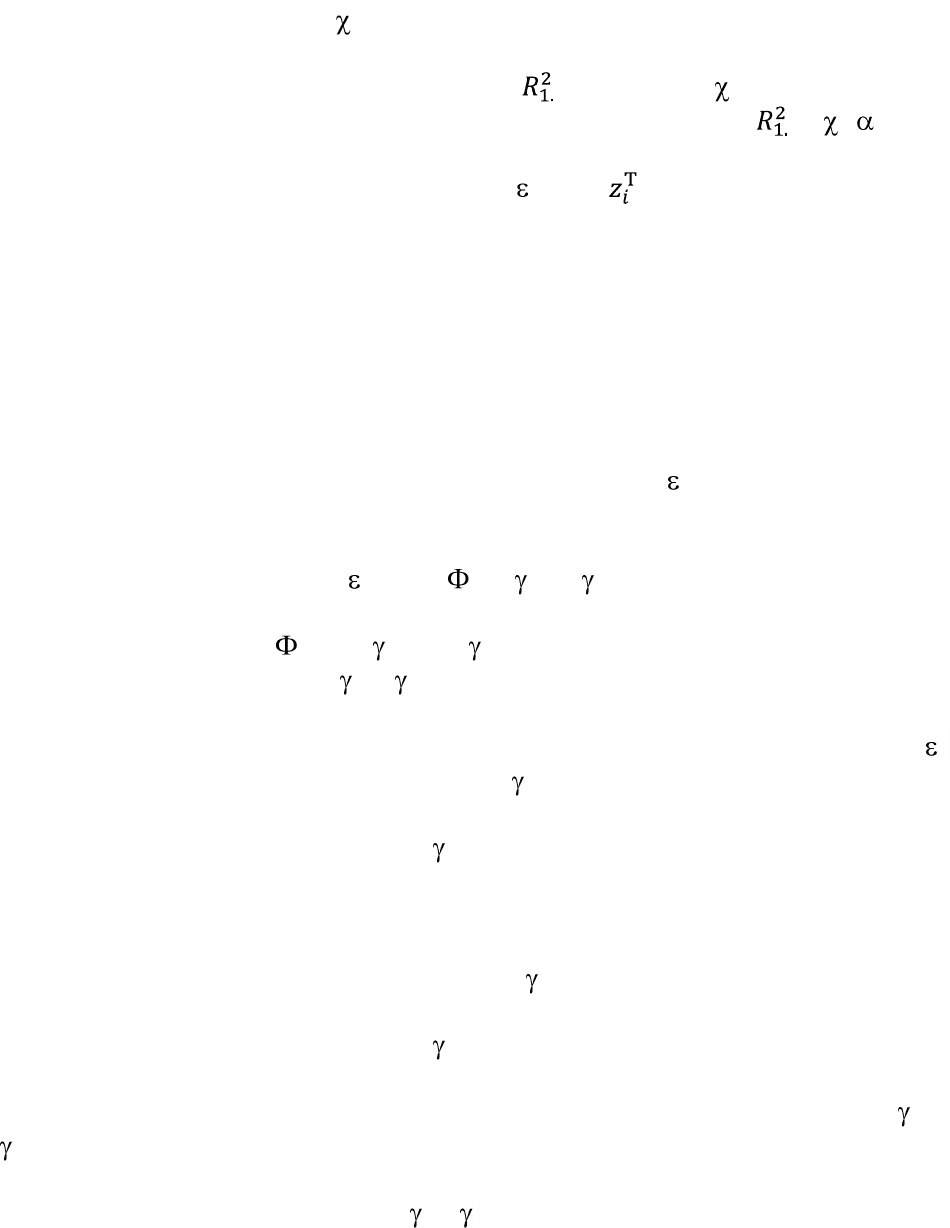
20
(5.21) имеет распределение
2
с числом степеней свободы, равным l. Поэтому,
чтобы проверить нулевую гипотезу (5.20) с помощью LM критерия,
необходимо сравнить значение статистики с квантилем
2
распределения с
соответствующим числом степеней свободы, равным l. Если >
2
( ,l), то
нулевая гипотеза отвергается, и есть основания предполагать наличие
гетероскедастичности в остатках вида var(
i
) = kg( β).
Нормальность распределения возмущений пробит модели. Ещѐ
одним важным критерием для пробит моделей является критерий на
нормальность распределения возмущений. Для тестирования нормальности
возмущений мы можем использовать адаптированный критерий множителей
Лагранжа. Для этого мы выполним спецификацию распределения
возмущений несколько шире, чем нормальное распределение. И далее будем
проводить тестирование распределения возмущений при этом
предположении.
Параметризация распределения возмущений
i
проводится путѐм
определения функции распределения в следующем виде
Pr(
i
≤ t) = (t +
1
t
2
+
2
t
3
). (5.22)
Распределение вида (t +
1
t
2
+
2
t
3
), при введении дополнительных
ограничений на параметры
1
и
2
,
характерно для семейства распределений
Пирсона.
Добавить предположение об асимметрии распределения возмущений
i
мы можем задав ограничение на параметр
1
в следующем виде
1
≠ 0.
С другой стороны, мы можем предположить наличие тяжѐлых хвостов, или
эксцесса, в распределение возмущений модели. Тогда необходимо включить
ограничения об отличии от нуля параметра
2
2
≠ 0.
Для нормального распределения оба ограничения об отличии параметров
1
и
2
от нуля отменяются и, следовательно, должно выполняться условие:
1
=
2
= 0.
Поэтому проверка на нормальность возмущений в пробит моделях сводится к
тестированию двух параметрических ограничений в функции распределения
вида:
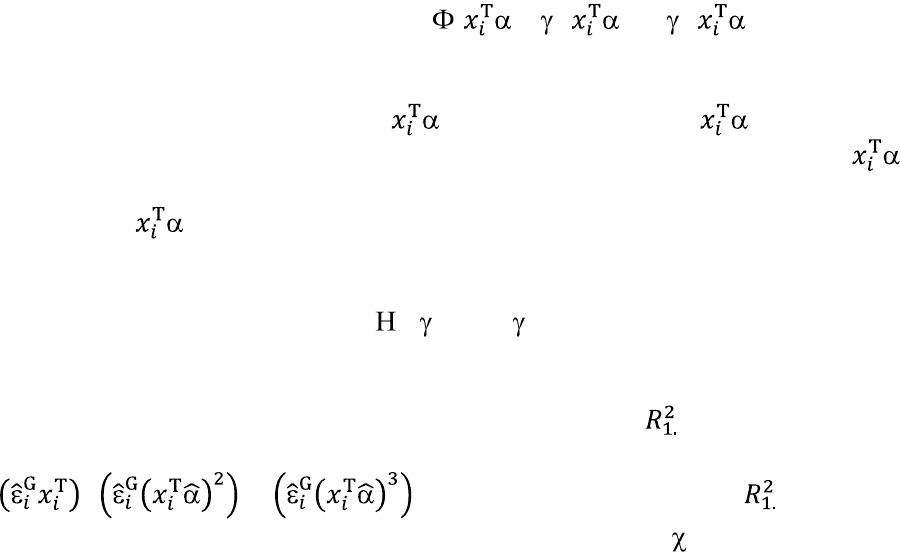
21
Pr(y
i
= 1| x
i
) = ( +
1
( )
2
+
2
( )
3
), (5.23)
или, к аналогичной процедуре проверки существенности влияния
пропущенных квадратичной ( )
2
и кубической ( )
3
переменных
соответственно. Как мы уже отмечали, значимый квадратичный член ( )
2
в
(5.23) свидетельствует о наличии асимметрии. Значимое кубическое
слагаемое ( )
3
говорит о существовании эксцесса в виде тяжѐлых хвостов.
Нулевая гипотеза в процедуре проверки формулируется как:
0
:
1
= 0 и
2
= 0. (5.24)
Статистику для критерия можно получить несколькими способами: например,
напрямую вычисляя (5.21). Но легче всего найти , выполнив оценку
вспомогательной регрессии вектора единиц на переменные, заданные через
, и , и затем n раз вычисляя . Если верна
нулевая гипотеза, то статистика имеет распределение
2
с двумя степенями
свободы.
5.5. Модели множественного выбора. Модели с латентными
переменными
Модели множественного выбора (Multi-response Models) представляют
собой особый класс моделей. Их применяют, когда зависимая переменная
может иметь несколько возможных альтернативных значения. Например,
рассматривая место жительства можно выбрать крупный город, город
среднего размера, малый город, село; или количественная зависимая
переменная может принимать значения только в определѐнных областях,
когда в анкетах, например, по каким-то причинам не требуется указывать
точное значение, достаточно отнести респондента к определѐнной группе.
Как и модели бинарного выбора, модели множественного выбора описывают
вероятности исходов зависимой переменной. Однако в отличие от моделей
бинарного выбора, модели множественного выбора представляют
вероятность исходов зависимой переменной как функцию альтернативных
значений, которые определяются набором характеристик модели.
Различают два типа моделей множественного выбора: модели с
упорядоченными откликами, и модели с неупорядоченными откликами.
Модели с упорядоченными откликами предполагают существование
логической упорядоченности альтернатив, благодаря упорядоченности
откликов, они описывают поведение зависимой переменной более
экономичным способом.

22
Можно утверждать, что если существуют скрытые механизмы,
определяющие выбор между альтернативами, то результаты могут оказаться
чувствительными к порядку появления альтернатив.
Модели с неупорядоченными альтернативными исходами значений
зависимой переменной нечувствительны к нумерации альтернатив. Часто они
предполагают, что уровень полезности разных альтернатив для индивида
носит случайный характер, и индивиды выбирают ту альтернативу, которая,
как они считают, принесѐт им наибольшую полезность.
Вначале подробнее рассмотрим модели упорядоченных откликов.
Предположим, что существует ограниченный набор логически
упорядоченных альтернатив, которые пронумерованы соответствующим
образом от 1 до M. Описать модель можно несколькими способами. Удобно
это сделать, применив подход, опирающийся на использование латентных
зависимых переменных. Рассмотрим постановку модели с латентными
зависимыми переменными.
Для описания модели будем использовать латентные зависимые
переменные y
i
*
, которые определим следующим образом:
y
i
*
= +
i
, (5.25)
y
i
= j, если
j-1
< y
i
*
≤
j
. (5.26)
Интервал значений, который пробегает латентная зависимая переменная y
i
*
,
может быть достаточно широк. Мы допускаем, что латентная зависимая
переменная y
i
*
принимает значения от - ∞ до + ∞, тогда границы изменения
значений зависимой переменной задают начальный и конечный параметры:
0
и
M
. Кроме того, мы определим ещѐ одну важную пограничную точку, в
которой происходит качественное изменение значений вероятности. Чаще
всего такой точкой выступает ноль. Тогда мы получаем как минимум три
точки, которым соответствую параметры:
0
= -∞;
1
= 0;
M
= ∞.
Тогда, вероятность того, что будет выбрана альтернатива j, равна
вероятности того, что латентная переменная лежит в указанных параметрами
j-1
и
j
границах, см. условие (5.26).
Распределение возмущений, как и в моделях бинарного выбора,
определяет тип используемой модели: логит или пробит. Так стандартное
нормальное распределение возмущений даѐт упорядоченную пробит модель,
а экспоненциальное распределение возмущений встречается в
соответствующих логит моделях.
Приведѐм простой пример. Предположим, что зависимая переменная
имеет y
i
три возможных альтернативы. Первая состоит в том, что зависимая
переменная равна единице:
y
i
= 1, если y
i
*
≤ 0;
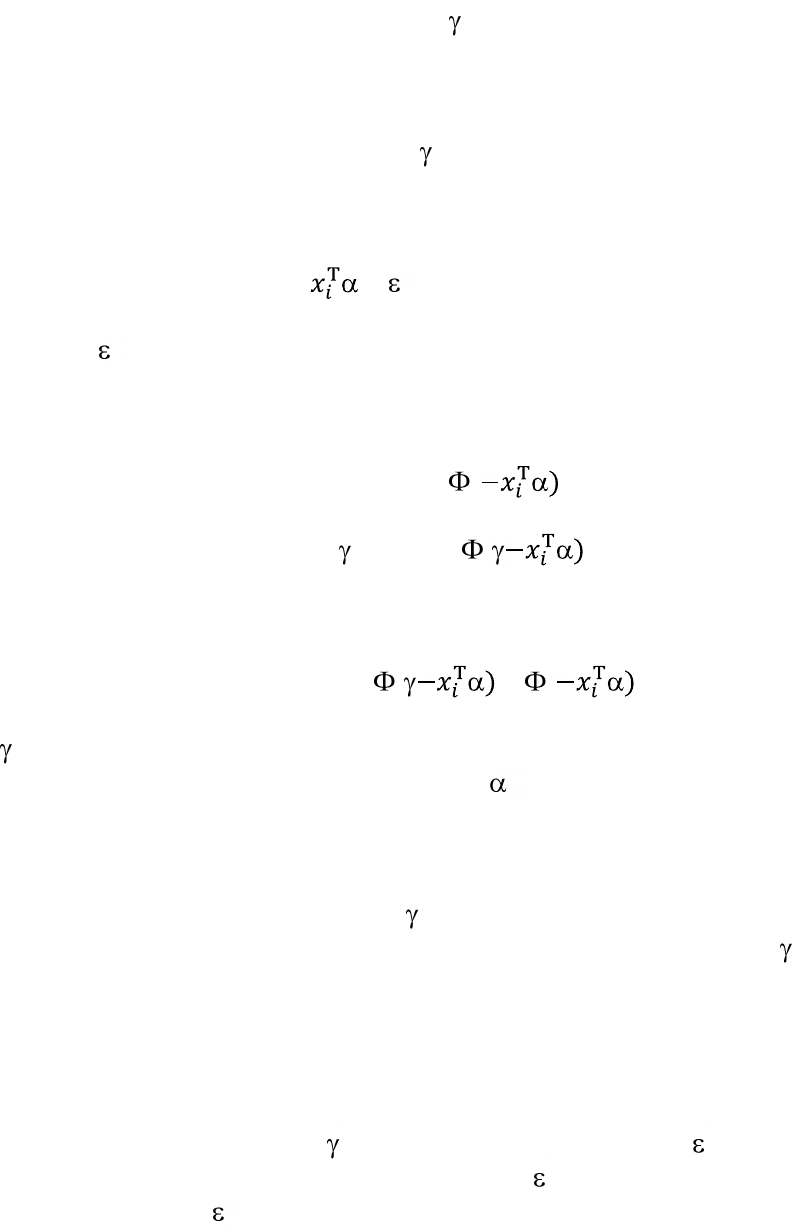
23
вторая, когда переменная равна двум:
y
i
= 2, если 0 < y
i
*
≤ ;
и, наконец, третья альтернатива возникает при условии, что
y
i
= 3, если y
i
*
> .
Латентная переменная определена как
y
i
*
= +
i
.
Если возмущения
i
имеют стандартное нормальное распределение, тогда
имеем дело с пробит моделью, и условные вероятности будут принимать
следующие значения:
Pr(y
i
= 1| x
i
) = Pr(y
i
*
≤ 0| x
i
) = ( ,
Pr(y
i
= 3| x
i
) = Pr(y
i
*
> | x
i
) = 1 – ( ,
или, что равнозначно,
Pr(y
i
= 2| x
i
) = Pr(y
i
*
≤ 0| x
i
) = ( – ( .
Параметр в приведѐнном примере оценивают совместно с другими
параметрами модели, объединѐнными в векторе , методом наибольшего
правдоподобия. Функция правдоподобия объединяет перечисленные выше
вероятности.
Следует отметить, что в разработке модели важную роль отводят
условию нормализации границ параметров
j
, а также масштабу латентных
зависимых переменных y
i
*
. В отсутствие нормализации границ параметров
j
,
возникает другая проблема – это проблема идентификации параметров
модели. Так в процессе оптимизации при отыскании максимума функции
наибольшего правдоподобия возможно установление разных комбинаций
параметров, которые могут привести к одинаковым значениям функции
правдоподобия. Поэтому нормализация здесь необходима. С учѐтом
нормализации границ параметров
j
, распределение ошибок
i
имеет
фиксированную дисперсию, равную единице, var(
i
) = 1, и нулевое
математическое ожидание E(
i
) =0.
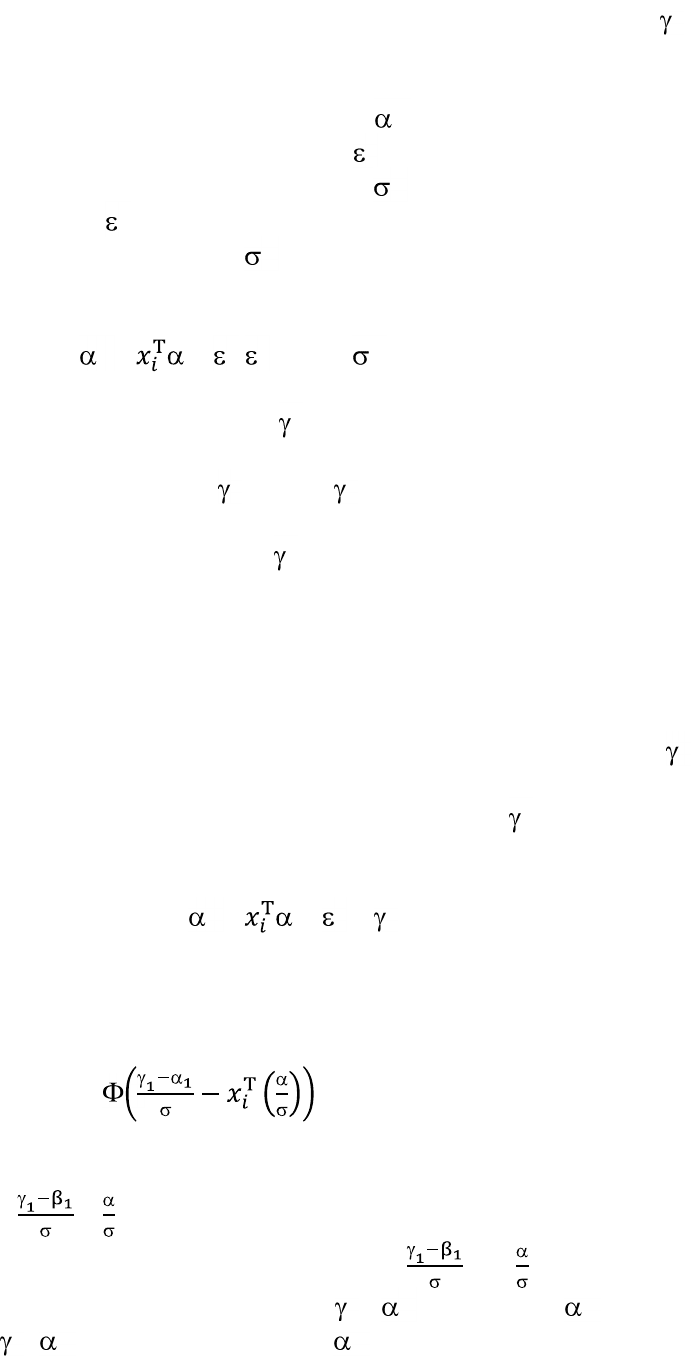
24
Проиллюстрируем необходимость нормализации границ параметров
j
.
Для этого перепишем вышеприведѐнный пример ещѐ раз, убрав при этом
условия нормализации. Это означает, что мы должны
1) устранить константу из вектора параметров ,
2) и допустить распределение возмущений
i
с дисперсией, равной не
единице, а скажем некоторой неизвестной величине
2
,
то есть предположить, что
i
независимо и одинаково распределены по
нормальному закону с параметрами N(0,
2
), для всех наблюдений выборки i
= 1, 2, …, n. Тогда, модель из рассмотренного примера принимает вид:
y
i
*
=
1
+ +
i
,
i
~ N(0,
2
),
y
i
= 1, если y
i
*
≤
1
;
y
i
= 2, если
1
< y
i
*
≤
2
;
y
i
= 3, если y
i
*
>
2
.
Как видим, вероятность, которая войдѐт в функцию правдоподобия,
определяется только теми наблюдениями, для которых можно
идентифицировать зависимую переменную. Зависимая переменная
наблюдаема и принимает целочисленные значения, равные 1, 2 или 3, при
условии, что латентная переменная y
i
*
находится в заданных параметрами
j
интервалах. Например, для y
i
= 1, условная по x
i
вероятность, с учѐтом того,
что латентная переменная принадлежит интервалу от – ∞ до , будет равна
следующему выражению
Pr(y
i
= 1| x
i
) = Pr(
1
+ +
i
≤
1
| x
i
).
Нетрудно убедиться, что указанная вероятность Pr(y
i
= 1| x
i
) равна
следующему значению функции нормального распределения:
.
Как видим, функция вероятности включает два смешанных выражения от
параметров, а именно: и . Оба выражения влияют на значение функции
правдоподобия. И тем не менее, оба выражения и , и могут быть
получены для разных сочетаний параметров
1
,
1
и вектора . Таким
образом, параметры
1
,
1
и элементы вектора не идентифицируемы при
реализации процедуры наибольшего правдоподобия. Поэтому для

25
идентификации параметров необходимо вводить дополнительные условия
нормализации.
Среди стандартных приѐмов нормализации, применяют, например,
такие:
2
= 1,
1
= 0.
Отмети, что условная вероятность, которая включена в функцию
наибольшего правдоподобия, не чувствительна к подобным ограничениям по
нормализации. Тем не менее, в связи с введением условий нормализации
появляется необходимость корректировать интерпретацию коэффициентов
модели множественного выбора.
5.6. Мультиноминальные модели.
Второй вариант моделей множественного выбора называют
мультиноминальными моделями. Необходимость использования
мультиноминальных моделей возникает, когда нет возможности упорядочить
альтернативные значения зависимой переменной. Рассмотрим несколько
подходящих к случаю примеров:
– индивидом рассматриваются альтернативы проживания в нескольких
городах, схожих по численности населения и условиям, таких как
Новосибирск, Красноярск, Иркутск;
– индивид выбирает способ передвижения к намеченному пункту из
всех возможных: самолѐт, поезд, автобус;
– рассматривается профессия участников выборки: учитель, врач,
юрист, экономист.
В таких достаточно типичных случаях рекомендуется использовать
мультиноминальные модели. Для проведения оценки требуется наложить
определѐнную структуру на вероятности разных альтернатив.
Проанализируем полезность индивида при выборе альтернатив,
которые мы обозначим через q. Рассмотрим случайную структуру
полезности, когда альтернативы расположены в произвольном порядке.
Предположим, что мы выбираем из Q альтернатив, q = 1,2, …, Q. Каждая
альтернатива q для индивида i имеет некоторую полезность. Уровень
полезности, которого достигает индивид, задается некоторой функцией U
iq
.
Индивиды выбирают альтернативу с наивысшей полезностью.
К сожалению, уровень полезности является ненаблюдаемой величиной.
Поэтому необходимо сделать некоторые дополнительные предположения,
чтобы появилась возможность формализовать и оценить модель. Первое
допущение, которое мы сделаем, касается общего вида функции полезности.
Мы предположим, что полезность каждой альтернативы является линейной
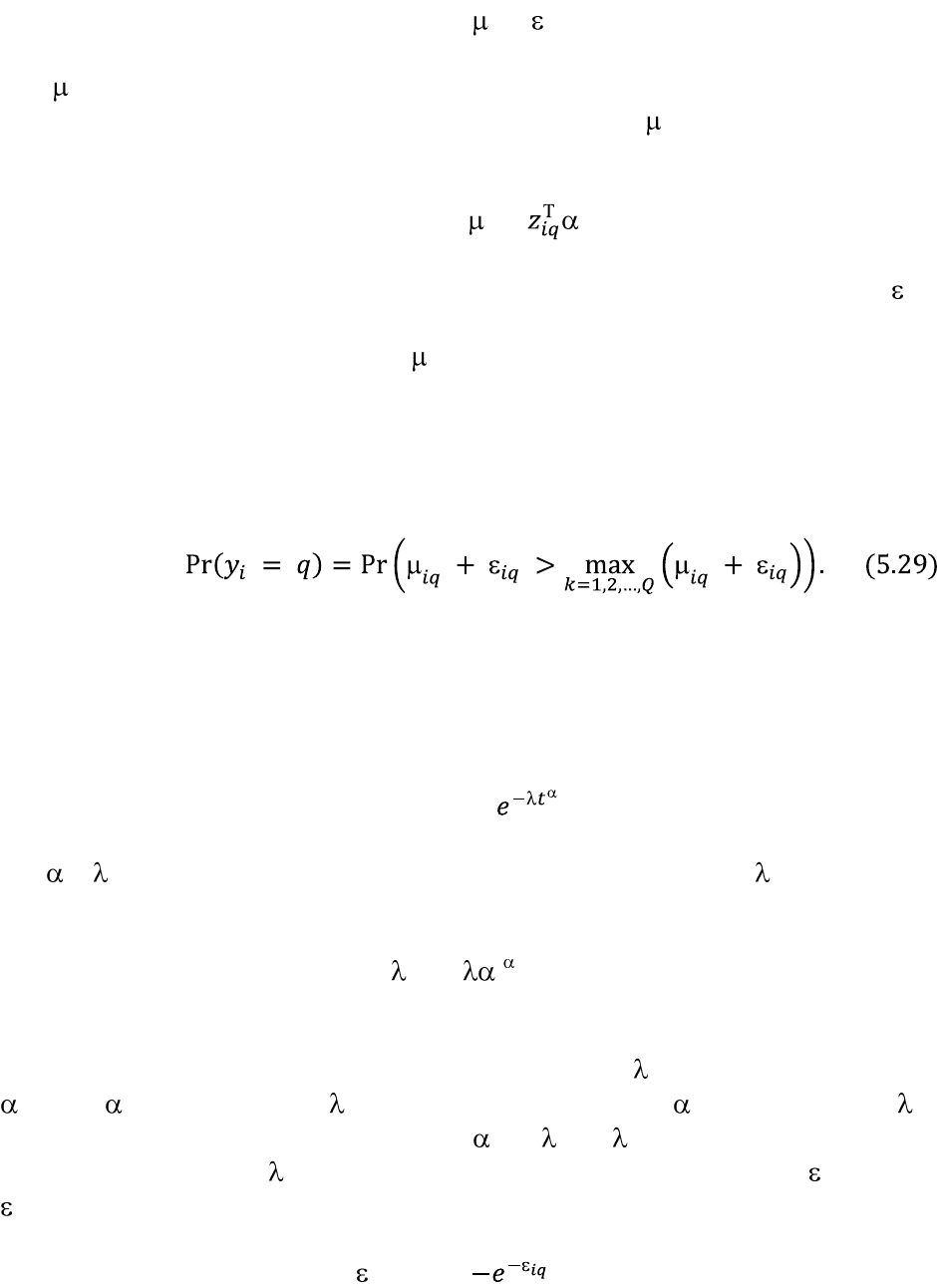
26
функцией наблюдаемых индивидуальных характеристик объектов и
возмущений:
U
iq
=
iq
+
iq
, (5.27)
где
iq
– детерминированная функция наблюдений и ограниченного числа
неизвестных параметров. Мы предположим, что
iq
представляет собой
линейную функцию наблюдаемых переменных z вида:
iq
= , (5.28)
где (i) – индекс объектов выборки, (q) – индекс альтернативных исходов.
iq
–
ненаблюдаемая ошибка, мы предполагаем, что возмущения имеют некоторое
распределение. Таким образом,
iq
могут варьироваться как по объектам
выборки и альтернативам исходов, так и по обоим индексам одновременно.
Исходя из сделанных предположений, найдѐм вероятность того, что индивид
выбирает исход с индексом q. Очевидно, что вероятность выбора исхода
равна
В (5.29) мы встречаем функцию определения максимума от нескольких
случайных величин. Эту проблему можно решить, используя некоторые
известные распределения, например распределение Вейбулла (Weibull),
которое имеет вид:
F(t) = 1 − ,
где и − неизвестные параметры распределения, а функция (t) определена
как
(t) = t
−
1
.
Для распределения Вейбулла характерны следующие особенности. Так
возрастающий или убывающий характер поведения (t) зависит от параметра
: при > 1 функция (t) возрастающая, а при < 1 функция (t)
соответственно убывающая. Тогда при = 1 (t) = .
Определив, что = 1, функция распределения возмущений
iq
, при t =
iq
, будет определена следующим образом:
F(
iq
) = exp( ). (5.30)
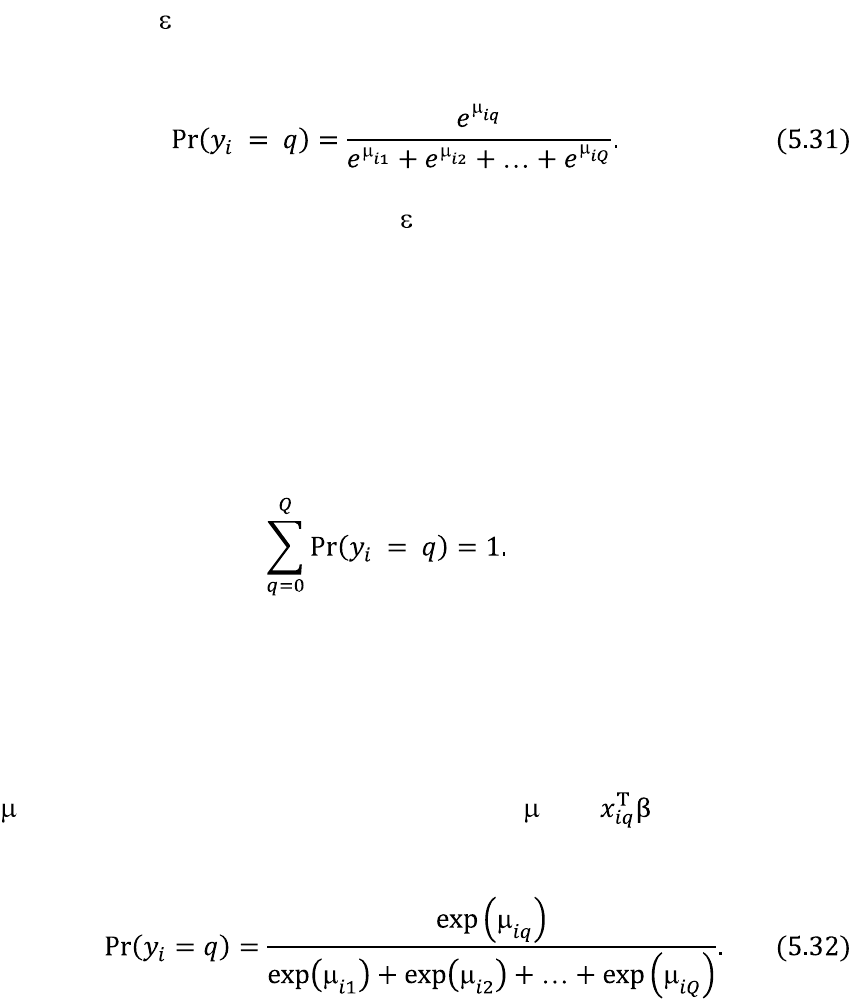
27
Предположим, что
iq
взаимно независимы, и имеют распределение (5.30).
Тогда вероятность выбора q-го исхода равна
Заданное распределение возмущений
iq
обладает рядом особенностей, в
частности:
1) оно гарантирует, что
0 ≤ Pr(y
i
= q) ≤ 1;
2) а также
3) позволяет установит масштаб переменной, характеризующей полезность,
который в, общем случае, не установлен.
Нормализация устанавливается следующим образом: один из
детерминированных уровней полезности приравнивается к нулю. Пусть это
будет
i1
= 0. И пусть, для определѐнности,
iq
= . Это даѐт нам
следующее выражение для вероятности Pr(y
i
= q):
Выражение (5.32) называют мультиноминальной логит моделью, или
независимой логит моделью.
Очевидно, что при наличии только двух альтернатив
мультиноминальный логит сводится к обычной логит модели бинарного
выбора: вероятность выбора альтернативы q со стороны отдельного индивида
представляют собой простое выражение вероятности от объясняющих
переменных и ненаблюдаемых возмущений. На основе вероятностей вида
(5.32) строят функцию наибольшего правдоподобия, и модель соответственно
оценивают методом наибольшего правдоподобия.
