Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.


8
широко используют для формулировки моделей с ограничениями на
зависимые переменные. Одна из особенностей моделей с ненаблюдаемыми
переменными заключается в трактовке латентных переменных. Зачастую их
рассматривают как переменную, отражающую изменение в уровне
полезности изучаемых благ для потребителей. В дальнейшем мы рассмотрим
несколько вариантов таких моделей.
Введѐм новую переменную, пусть y
i
*
- ненаблюдаемая зависимая
переменная, еѐ проявления мы фиксируем через переменную y
i
, которая
принимает значения либо y
i
*
, либо ноль в зависимости от значения
ненаблюдаемой переменной,
i
– как прежде отражает влияние случайных
возмущений. Тогда пробит модель можно описать как
y
i
*
= x
i
T
+
i
,
y
i
= y
i
*
при y
i
*
> 0;
y
i
= 0 при y
i
*
≤ 0. (5.8)
i
не зависят от x
i
, независимы и одинаково распределены по нормальному
закону с параметрами
i
~ N(0, 1).
Возвратимся к примеру о наличии собственного жилья у семьи в
зависимости от уровня доходов, других объясняющих переменных x
i
и
ненаблюдаемых характеристик
i
. Прежде всего отметим, что y
i
*
можно
интерпретировать как разность между уровнями полезности в двух
ситуациях: иметь жильѐ на правах собственника, или проживать в
арендованном жилье. Величина y
i
*
предстаѐт перед нами как ненаблюдаемая
переменная. Тогда семья предпочтѐт иметь жильѐ на правах собственника,
если прирост полезности от приобретения жилья y
i
*
превышает некоторый
минимальный уровень, в нашем примере – ноль: y
i
*
> 0. Тогда наблюдаемая
величина будет равна y
i
= 1, то есть семья предпочитает иметь собственное
жильѐ, если y
i
*
> 0. Если полезность от владения собственным жильем ниже,
чем полезность проживания в арендованной квартире: y
i
*
≤ 0, то y
i
= 0.
Вероятность, что y
i
= 1 с учѐтом (5.38) будет определена как
Pr(y
i
= 1) = Pr (y
i
*
> 0) = Pr(x
i
T
+
i
> 0) = Pr(-
i
≤ x
i
T
) = F(x
i
T
),
где F – функция распределения случайной величины (−
i
), например,
нормальная или логистическая. Так как в общем случае функция F
симметричная, то функции распределении (−
i
) и (
i
) будут совпадать. А
модель бинарного выбора в постановке с латентной зависимой переменной
сводится к модели распределения случайной составляющей
i
.
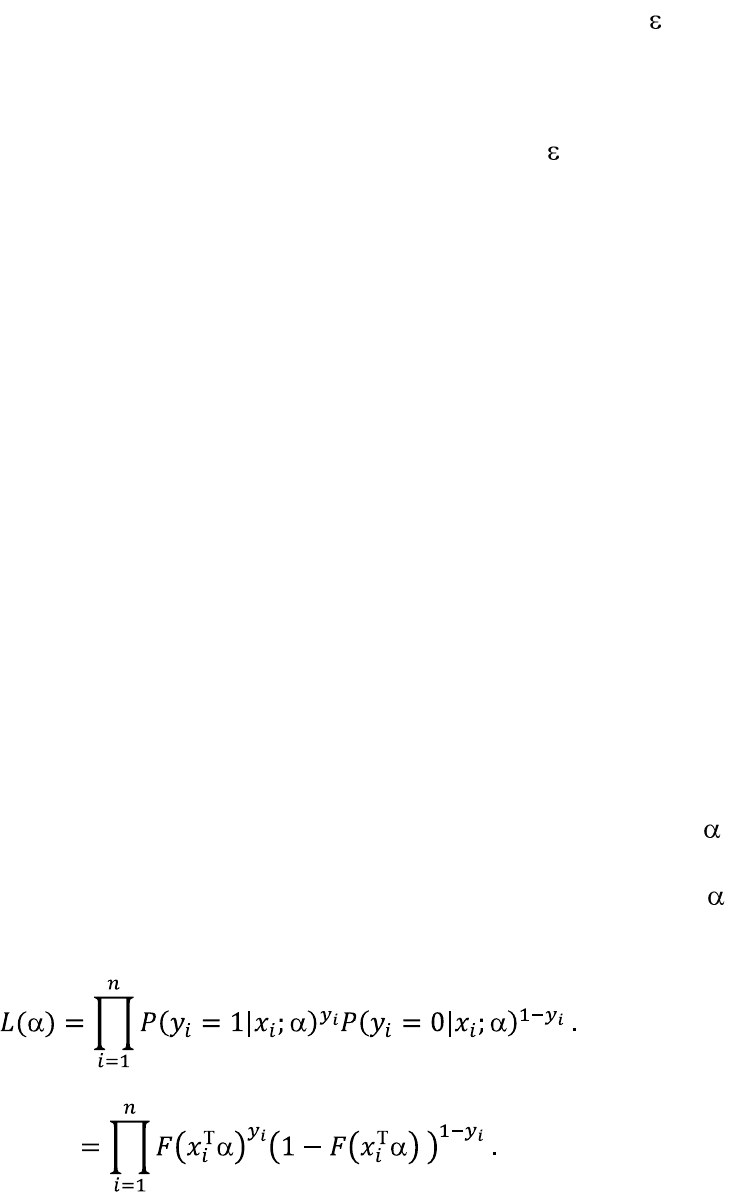
9
Одна из основных проблем оценивания модели с заданной функцией
полезности связана с необходимостью нормировок. Причина заключается в
том, что в модели не определѐн масштаб величины полезности, поэтому
требуется нормировать распределение возмущений таким образом, чтобы
привести его к известному распределению, например, к стандартному
нормальному распределению. Нормировку по приведению к стандартному
нормальному распределению мы можем провести, задав дисперсию
i
равной
единице.
Отметим, что выбирая из возможных законов распределения
возмущений, мы получаем разные постановки модели бинарного выбора.
Если мы выбираем стандартное нормальное распределение
i
, то из модели с
ненаблюдаемой зависимой переменной получим пробит модель, если будем
предполагать, что в модели (5.8) возмущения распределены по
логистическому закону, то модель трансформируется в логит.
Позже мы увидим, что постановка и формальная запись моделей
бинарного выбора, таких как побит модели, с использование латентных
переменных практически полностью совпадает с формальной записью
стандартных тобит моделей.
5.2. Оценка логит и пробит моделей
Оценки параметров модели бинарного выбора можно получить с
использованием метода наибольшего правдоподобия. Не останавливаясь
подробно на реализации самого метода наибольшего правдоподобия, который
мы уже рассматривали, обсудим проблемы оценивания логит и пробит
моделей. Разделим результаты наблюдений в зависимости от значений
зависимой переменной и еѐ вклада в функцию правдоподобия: объединим все
положительные исходы, когда y
i
= 1, и все отрицательные исходы, когда y
i
=
0. Тогда функция правдоподобия будет определена как произведение
вероятностей всех положительных и всех отрицательных исходов.
Положительный результат определяется вероятностью: Pr(y
i
= 1| x
i
; ) в
соответствующей степени (y
i
); отрицательный результат, имеющий место при
y
i
= 0, будет равен вероятности отрицательного исхода в Pr(y
i
= 0| x
i
; ) в
степени (1 - y
i
), в итоге получим:
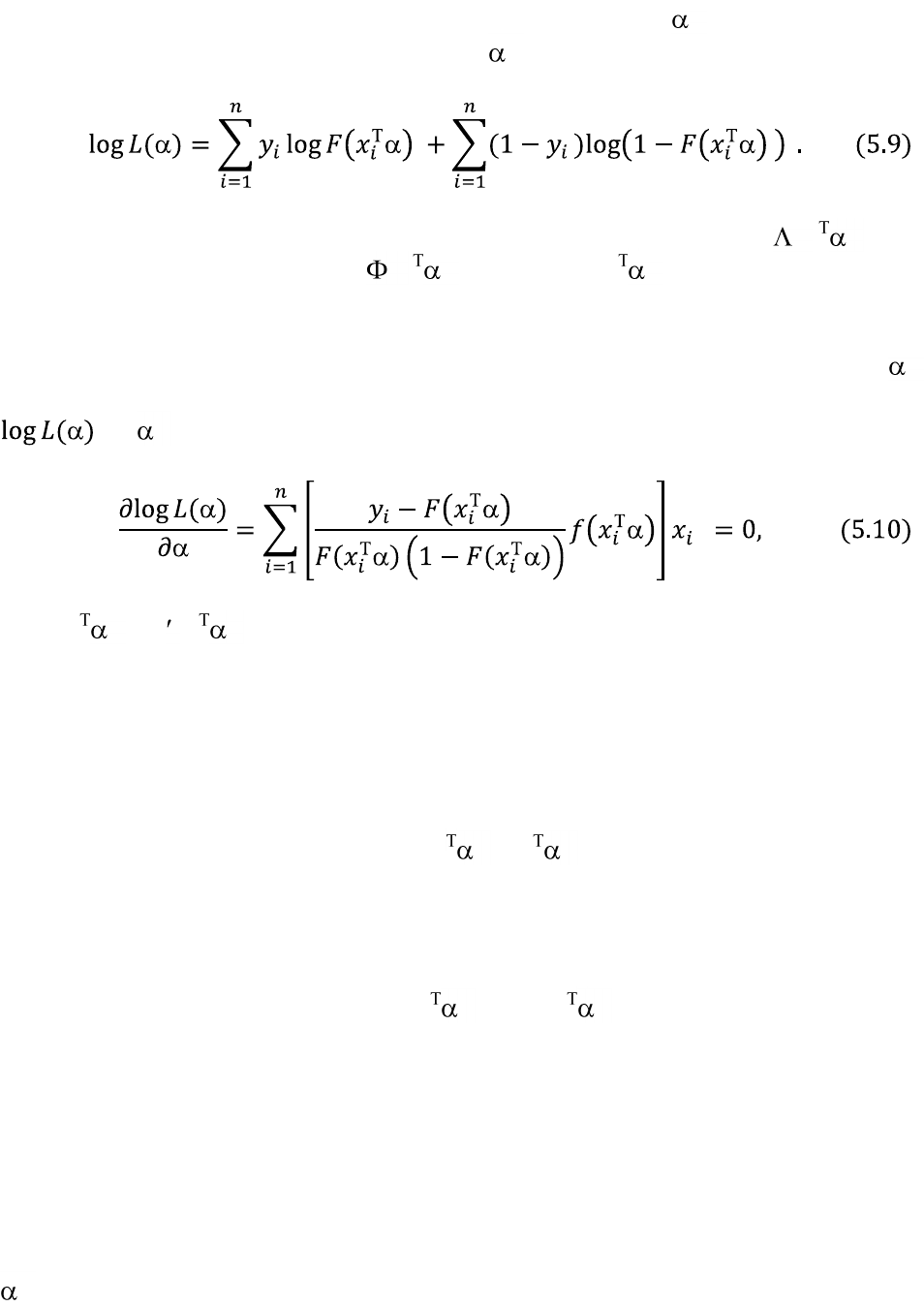
10
Логарифмирование функции правдоподобия L( ) даѐт нам лог-
линейную функцию правдоподобия log L( ):
Подстановка в (5.9) требуемой функции логистического (x
i
) или
нормального распределения (x
i
) вместо F(x
i
) позволит получить
соответствующее выражение для логит или пробит модели.
Оценка неизвестных параметров проводится путем отыскания
максимума значения функции (5.9) по параметрам, заключѐнным в векторе .
По условию первого порядка векторная производная лог-линейной функции
по должна быть равна нулю. Запишем это условие в общем виде:
где f(x
i
) = F (x
i
) функция плотности распределения случайной величины,
которая, как известно, совпадает с первой производной функции
распределения.
Учитывая значения, которые принимает зависимая переменная: 0 для
отрицательных исходов, или 1 – для положительных, выражение в
квадратных скобках в (5.10) будет равно
f(x
i
)/F(x
i
)
для наблюдений, в которых y
i
= 1, то есть когда мы наблюдаем исследуемое
явление; и определяется как
– f(x
i
)/(1 – F(x
i
))
для y
i
= 0, то есть в тех случаях, когда явление отсутствует. Выражение в
квадратных скобках имеет специальное называние – обобщѐнные остатки.
Условие (5.10) выполняется для всех переменных, объединѐнных в векторе x
i
,
и демонстрирует тот факт, что каждая объясняющая переменная, по условиям
первого порядка должна быть ортогональна обобщѐнным остаткам.
Таким образом, выражение (5.10) представляет собой ни что иное как
уже знакомую нам систему уравнений относительно неизвестных параметров
, решение которой даѐт нам требуемые оценки. С учѐтом конкретных
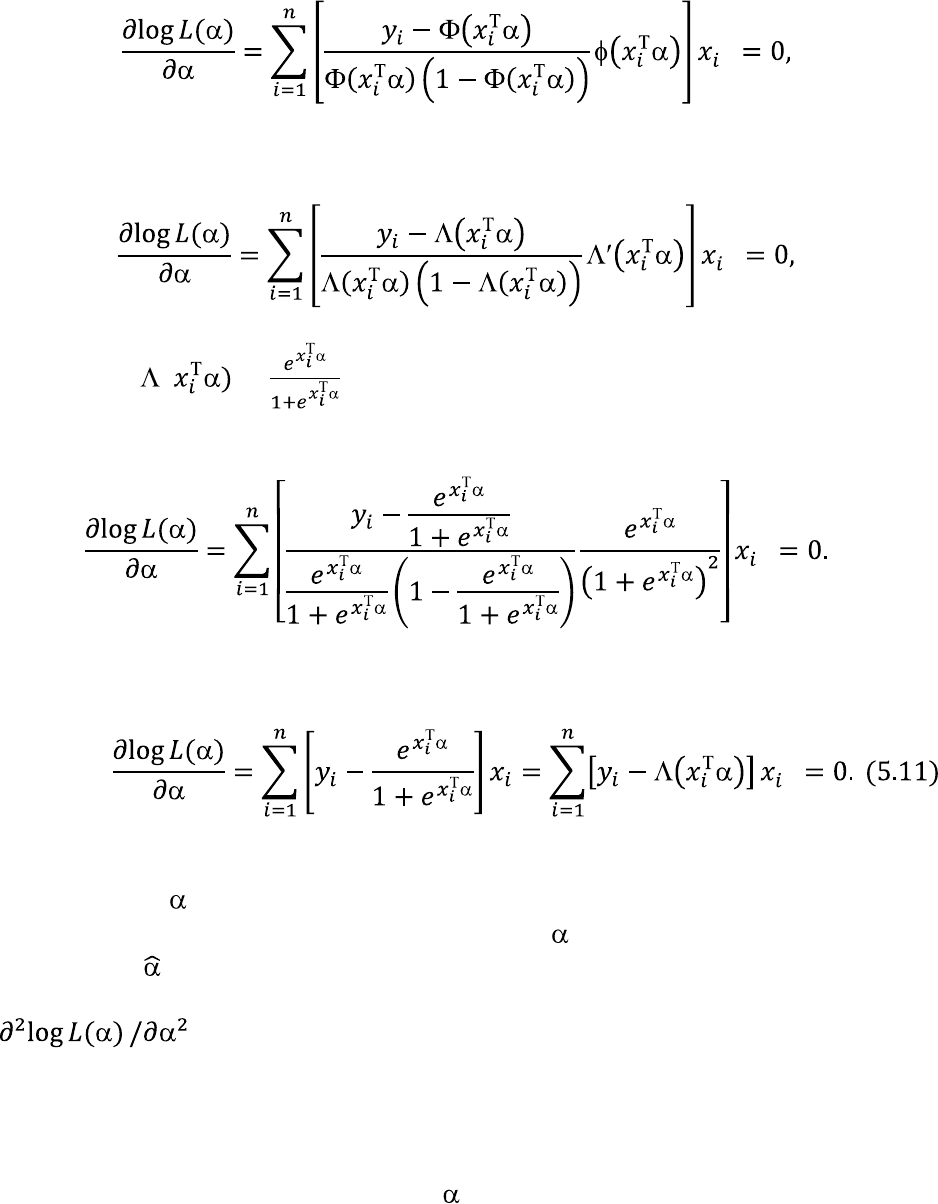
11
функций распределения система (5.10) трансформируется следующим
образом. Для нормального распределения и пробит модели система
принимает вид:
Для логистического распределения получим следующую трансформацию:
Подставив ( = , получим следующее выражение для системы
уравнений:
После привидения подобных членов выражение упростится:
Так как системы уравнений носят нелинейный характер, то решение системы
относительно возможно только численными методами. Решение выражения
(5.11) относительно вектора параметров даѐт нам правило оценки
параметров .
Что касается условий второго порядка, то матрица вторых производных
отрицательно определена, при условии, что точная
мультиколлинеарность в объясняющих переменных отсутствует. Поэтому
лог-линейная функция, а в силу свойств логарифмов и сама функция
правдоподобия, вогнута, что гарантирует нам сходимость итеративных
алгоритмов при поиске максимума функции правдоподобия.
С учѐтом полученных оценок , мы определим, с какой вероятностью
мы можно наблюдать изучаемое явление, то есть с какой вероятностью
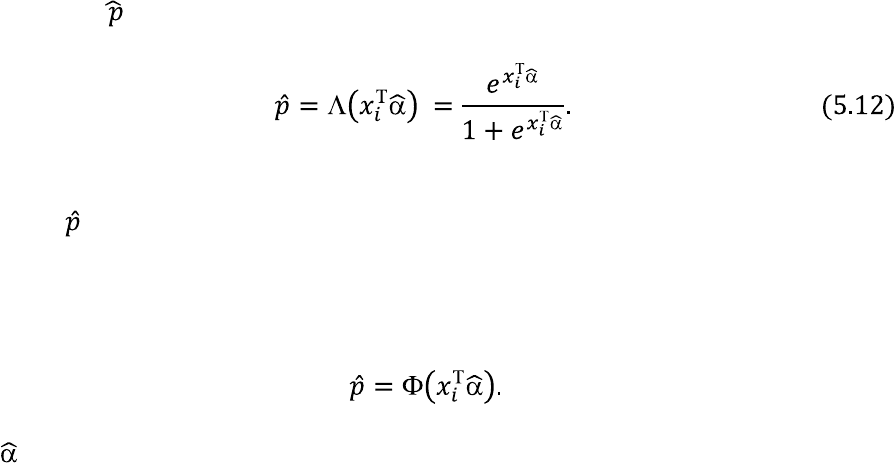
12
наблюдаемая зависимая переменная принимает значение один: y
i
= 1. Оценка
вероятности будет равна:
Говоря иными словами, предсказываемая частота появления
события в логит модели, будет равна наблюдаемой частоте, с которой
фиксируется появление переменной y
i
= 1.
Аналогичным образом будет определена частота появления событий в
пробит моделях:
где - оценка параметров пробит модели.
5.3. Показатели качества сглаживания для логит и пробит моделей
Нас интересует, как хорошо модель с качественной зависимой
переменной аппроксимирует данные выборки? Традиционным измерителем
точности сглаживания для линейной регрессии, оценивание которой
допустимо с использованием метода наименьших квадратов, выступает
коэффициент детерминации. Однако в силу нарушения ряда предположений
МНК, коэффициент детерминации в качестве такого измерителя не подходит.
Возникает вопрос, какой показатель, характеризующий сглаживание,
приемлем в случае, когда зависимая переменная – качественная? Предлагают
набор показателей.
В качестве показателей, сравнение которых позволяет получить
представление о преимуществе модели, могут быть использованы как
критерии, характеризующие точность сглаживания, так и показатели
сравнение степени корректности предсказаний на основе модели.
Существующие показатели точности сглаживания для моделей с
качественной зависимой переменной в основном построены по принципу
сравнения некоторых показателей двух вариантов модели: модели,
включающей набор всех объясняющих переменных, и модели с одной
константой.
Уравнение, которое включает только константу, можно
интерпретировать как модель с нулевыми ограничениями на параметры для
всех факторов, кроме константы, для которого вероятность появления
«успешных» событий будет равна:
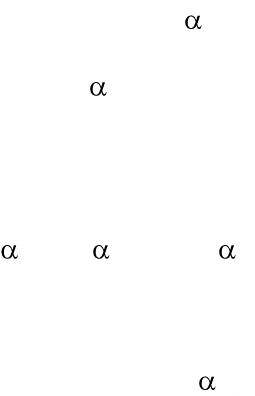
13
Pr(y
i
= 1) = F(
0
),
обозначим эту величину через p
0
: F(
0
) = p
0
.
Тестирование такого ограничения на параметры равносильно проверке
гипотезы о значимости уравнения регрессии. Тогда, если модель объединяет
p объясняющих переменных, то основную гипотезу можно записать как
Н
0
:
1
= 0,
2
= 0, …,
p
= 0
против альтернативной
Н
1
: хотя бы один из параметров
j
≠ 0, j = 1, 2, …, p.
Для определения значения критерия можно использовать отношение
правдоподобия. Расчѐт показателя проводится на основе значений функции
правдоподобия для расширенной модели (L
1
) и для модели с константой (L
0
).
Модель с полным набором объясняющих переменных должна обладать более
высокой объясняющей способностью, и для неѐ значение функции
правдоподобия, как и логарифм функции правдоподобия, должен быть выше,
чем для модели с константой, то есть должно выполняться условие:
log(L
1
) ≥ log(L
0
).
И, более того, так как лог-линейная функция наибольшего правдоподобия
является суммой логарифмов вероятностей, значения которых, как известно,
меньше единицы, то
0 > log(L
1
) ≥ log(L
0
).
Чем больше разница между логарифмами значений функций правдоподобия,
тем лучше расширенная модель объясняет поведение качественной
зависимой переменной по сравнению с моделью с ограничениями.
Критерий отношения правдоподобия для тестирования нулевой
гипотезы о значимости параметров можно вычислить как
LR = 2(ln L
1
– ln L
0
),
где ln – означает логарифмы соответствующих значений функции
правдоподобия.
Оценку log(L
1
) для критериев мы получаем в процедуре оценки модели
с полным набором объясняющих переменных. Получить оценку log(L
0
) как
для логит, таки и для пробит моделей, можно способом аппроксимации.
Аппроксимация log(L
0
) может быть выполнена следующим образом. Вначале
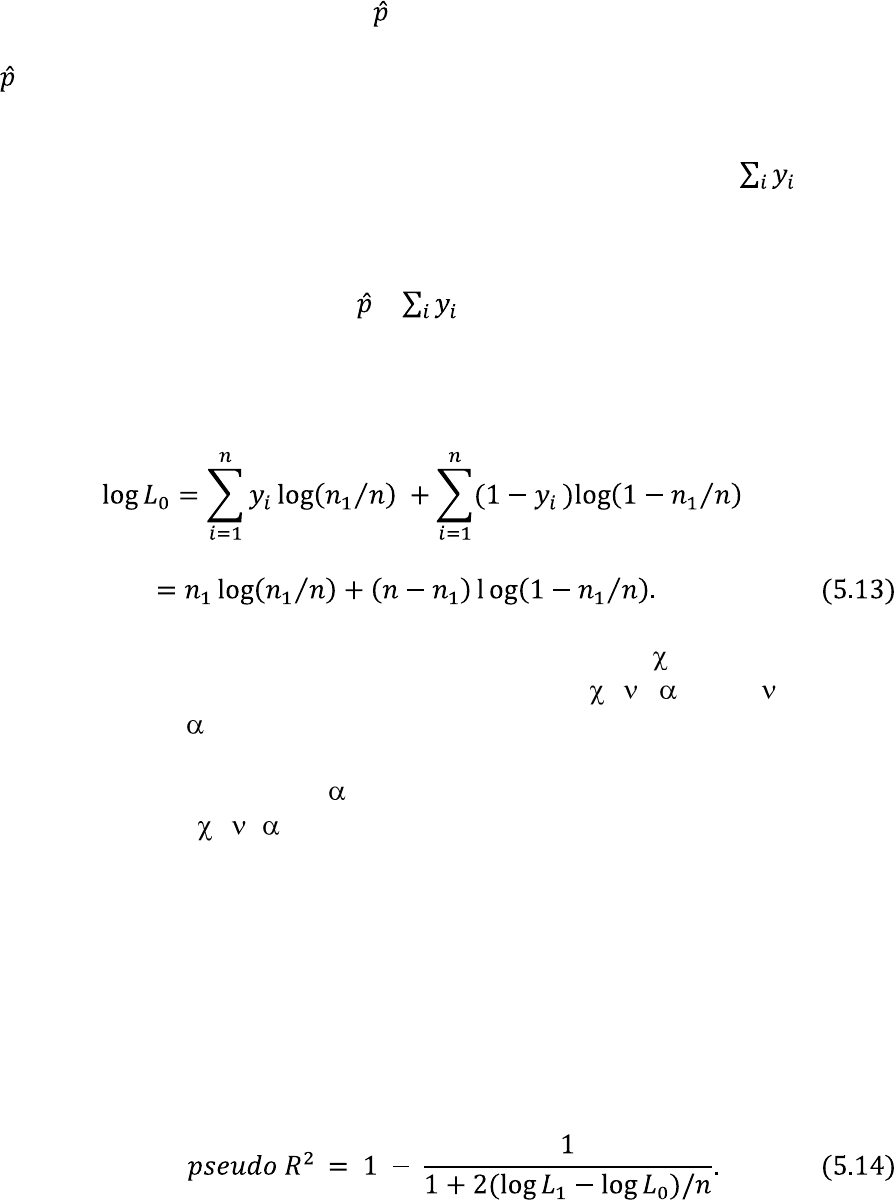
14
найдѐм оценку вероятности появления положительных исходов. Рассмотрим
все y
i
, для которых Pr(y
i
= 1) = p
0
. Тогда оценка p
0
будет равна:
= n
1
/ n,
где – выборочная частота положительных исходов, n – объѐм выборки; n
1
–
число положительных исходов в которых y
i
= 1, учитывая, что зависимая
переменная принимает только два значения: 0 и 1, число положительных
исходов равно сумме значений зависимой переменной: n
1
= . Тогда
выборочную оценку частоты реализации «успешных» событий можно найти
просто как
= / n.
Наибольшее значение лог-линейной функции наибольшего правдоподобия
для модели с ограничениями на параметры будет равно:
Если нулевая гипотеза верна, то LR критерий имеет
2
распределение с
числом степеней свободы, равным p. При LR >
2
( , ), где − число
степеней свободы, − уровень значимости, расчѐтная статистика попадает в
критическую область, в которой нулевая гипотеза отвергается, следовательно,
хотя бы один из параметров
j
≠ 0, j = 1, 2, …, p, и уравнение в целом
значимо. При LR <
2
( , ) статистика попадает в область принятия нулевой
гипотезы, и у нас нет оснований еѐ отвергать, и следует сделать вывод о том,
что модель незначима.
Рассмотрим показатели точности сглаживания. Основанные на
сравнении значений функции правдоподобия.
Первый из рассматриваемых нами показателей точности сглаживания,
который называют pseudo R
2
(псевдо R
2
), включает разность значений
логарифмов функций правдоподобия для сравниваемых моделей (log(L
1
) -
log(L
0
)) как составной элемент. Критерий определяют как
В (5.14) n – показывает объем выборки. Как и коэффициент детерминации,
псевдо R
2
изменяется в интервале [0, 1], и имеет сходную интерпретацию в
15
рамках допустимых значений. Если в модели отсутствуют значимые факторы,
объясняющие поведение зависимой переменной, то соответствующие оценки
параметров расширенной модели не значимы, и, следовательно, лог-
линейные функции правдоподобия будут примерно одинаковы, или
отличаться в пределах ошибки оценивания: log(L
1
) ≈ log(L
0
). Поэтому
значение дроби в (5.14) будет примерно равно единице, а критерий pseudo R
2
будет приближаться к нулю.
Если, напротив, в модель включены значимые объясняющие
переменные, которые позволяют достаточно точно воспроизвести
наблюдаемые значения зависимой переменной, то функция наибольшего
правдоподобия log(L
1
) будет приближаться с отрицательной стороны к нулю.
Это означает, что знаменатель (5.14) будет расти, значение дроби падать, а
величина критерия pseudo R
2
приближаться к единице. Чем ближе значение
критерия к единице, тем лучше расширенная модель объясняет поведение
качественной зависимой переменной по сравнению с тривиальной моделью,
построенной на основе константы.
Коэффициент pseudo R
2
, имеет достаточно широкую сферу применения
помимо области моделей с качественными зависимыми переменными.
Другой измеритель качества сглаживания носит название автора, его
дословно называют как «R
2
по МакФаддену»: McFadden R
2
. Другое название
критерия – индекс отношение правдоподобия. Действительно, значение
критерия по Макфаддену определяют с учѐтом отношения логарифмов
функций наибольшего правдоподобия двух моделей: модели без ограничений
на параметры с полным набором объясняющих переменных и модели с
ограничениями на параметры. Формула критерия имеет следующий вид:
McFadden R
2
= 1 - log(L
1
)/log(L
0
) (5.15).
Интервал изменения значений критерия McFadden R
2
, как и интервал
изменения pseudo R
2
, простирается от 0 до 1. Как видно из формулы, при
log(L
1
) = 0, чисто теоретически, значение показателя строго равно единице.
Если log(L
1
) ≈ log(L
0
), то величина критерия приближается к нулю.
Другой подход для оценивания точности сглаживания опирается на
сравнение степени корректности предсказаний на основе модели. Для
предсказания значений качественной зависимой переменной, то есть для
оценки того, будет ли переменная равна единице y
i
= 1, или не будет,
рассматривают оценку вероятности, которая рассчитывается на основе
модели.
За основу принимают предположение, что, в общем случае, для
симметричного относительно нуля распределения вероятность появления
нулевого исхода равна F(0) = 1/2. Поэтом, оценивая вероятность
положительного исхода для y
i
= 1, предполагают, что
16
F( ) > 1/2 при > 0.
Тогда возможность появления единичного исхода обусловлена
положительным значением оценки вероятности:
i
= 1, если > 0;
и нулевого исхода – отрицательным значением оценки вероятности
соответственно:
i
= 0, если ≤ 0. (5.16)
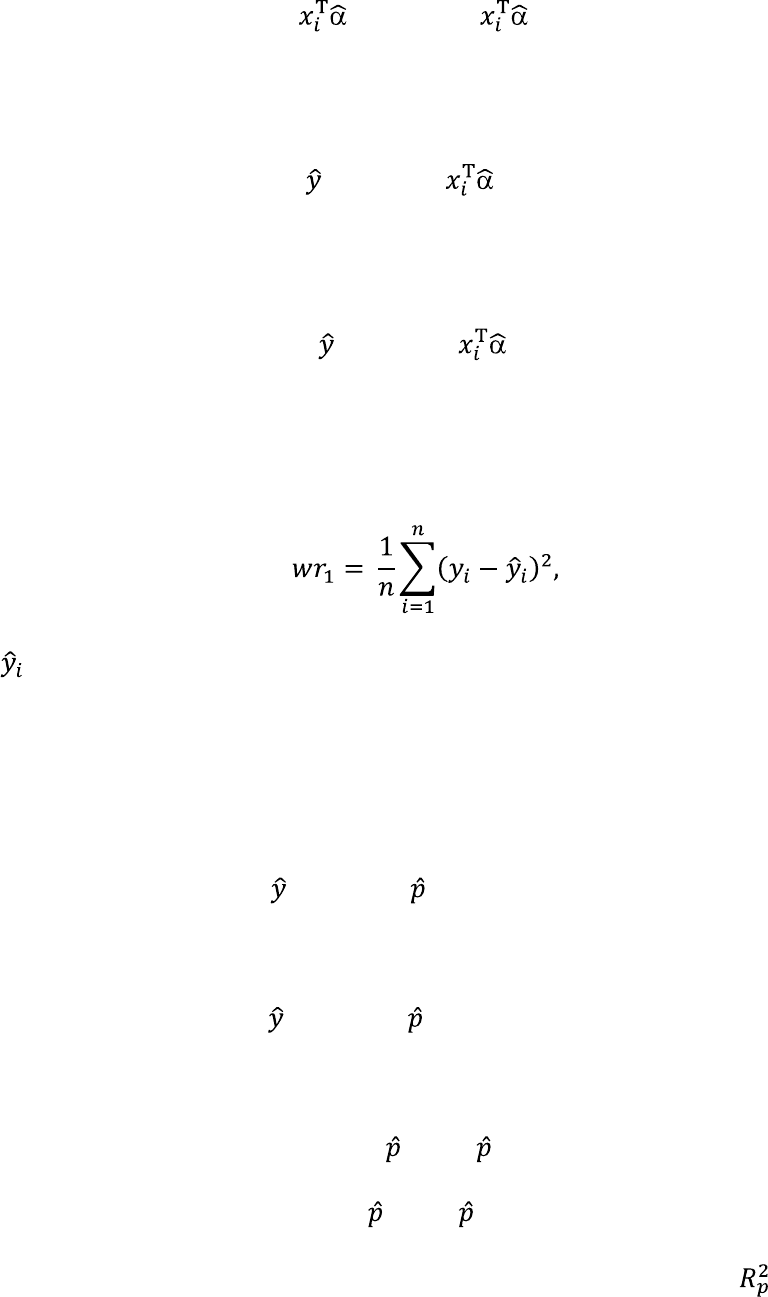
Долю неверных предсказаний для расширенной модели, то есть для модели с
полным набором объясняющих переменных, можно определить с помощью
следующего покзателя:
где − расчѐтные значения зависимой переменной, полученные на основе
расширенной модели.
Результат оценки показателя wr
1
сравнивают с долей некорректных
предсказаний wr
0
, оценѐнных с помощью модели с ограничениями на
параметры, в которую входит только свободный член. Для модели с
ограничениями предсказание зависимой переменной будет равно единице
i
= 1, если = n
1
/ n > 1/2,
и нулю
i
= 0, если = n
1
/ n ≤ 1/2.
Тогда доля неверных предсказаний wr
0
будет определена как
wr
0
= 1- , если > 0,5,
и
wr
0
= , если ≤ 0,5.
Мерой точности аппроксимации будет служить коэффициент , который
определяют как

17
= 1 - . (5.17)
В отличие от вышерассмотренных критериев, коэффициент , в силу
специфики своего построения, может принимать как положительные, так
отрицательные значения. Отрицательные величины коэффициента
возникают, когда расширенная модель предсказывает хуже, чем модель с
ограничениями на параметры, тогда wr
1
> wr
0
и, следовательно, отношение
wr
1
/wr
0
> 1. Такая ситуация достаточно редка, но возможна.
5.4. Критерии на спецификацию в моделях бинарного выбора.
Оценки метода наибольшего правдоподобия являются состоятельными.
Однако для того, чтобы гарантировать выполнение этого свойства
необходимо, чтобы модель, как и функция наибольшего правдоподобия,
имели правильную спецификацию, то есть необходимо правильно определить
функцию распределения данных.
Ошибки спецификации, а, следовательно, и несостоятельность оценок,
могут быть вызваны рядом причин:
– влиянием латентных (ненаблюдаемых) переменных,
– неверным составом объясняющих переменных, в частности,
отсутствием пропущенных переменных,
–несоответствием распределения возмущений
i
нормальному закону
распределения,
– гетероскедастичностью остатков
i
.
Проверить спецификацию распределения зависимой переменной y
i
как
функции регрессии от набора объясняющих переменных x
i
, то есть
спецификацию модели с точки зрения состава объясняющих переменных,
можно в рамках критерия множителей Лагранжа (LM). Критерий множителей
Лагранжа разработан на основе сравнения условий первого порядка
расширенной модели, включающей наиболее полный набор объясняющих
переменных и модели с ограничениями на параметры. С помощью критерия
множителей Лагранжа можно протестировать любой набор линейных
ограничений на параметры, в том числе сравнение с регрессией на константу.
Тестируется предположение о значимости отдельных элементов
спецификации в расширенной модели и модели с ограничениями на
параметры.
Предположим, нулевая гипотеза утверждает, что l пропущенных
переменных z
i
, не оказывают значимого влияния на зависимую переменную:
0
:
1
= 0,
2
= 0, …,
l
= 0.
