Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.

8
= (I -
1
-
2
- … -
p
),
При условии обратимости матрицы получим, что математическое ожидание
Y
t
равно:
E[Y
t
] = = (I -
1
-
2
- … -
p
)
-1
α =
-1
α. (4.13)
В связи с полученным результатом отметим, что существование матрицы
обратной к является необходимым условием стационарности Y
t
.
Отсутствие автокорреляции в ошибках модели векторной авторегрессии
в форме (4.7) существенно облегчает проблему оценивания модели. Система
VAR в форме (4.7) выглядит как система внешне не связанных уравнений с
одинаковым набором объясняющих переменных или регрессиоров в правой
части. Поэтому формально все сводится к оцениванию системы внешне не
связанных уравнений. Для определения оценок параметров достаточно
использовать метод наименьших квадратов, применяя его сначала для одного
уравнения, затем для другого, и так далее, вплоть до оценки всех уравнений.
В итоге получаем оценку всех k уравнений. Полученные оценки параметров
будут состоятельными. Свойство состоятельности достигается благодаря
распределению возмущений модели типа белого шума, и отсутствию
корреляции возмущений с текущими и предшествующими значениями
совместно зависимых переменных Y
t
.
На базе оценѐнных уравнений можем найти ошибки e
t
= (e
1t
, e
2t
, …, e
kt
)
как
e
t
= Y
t
- ,
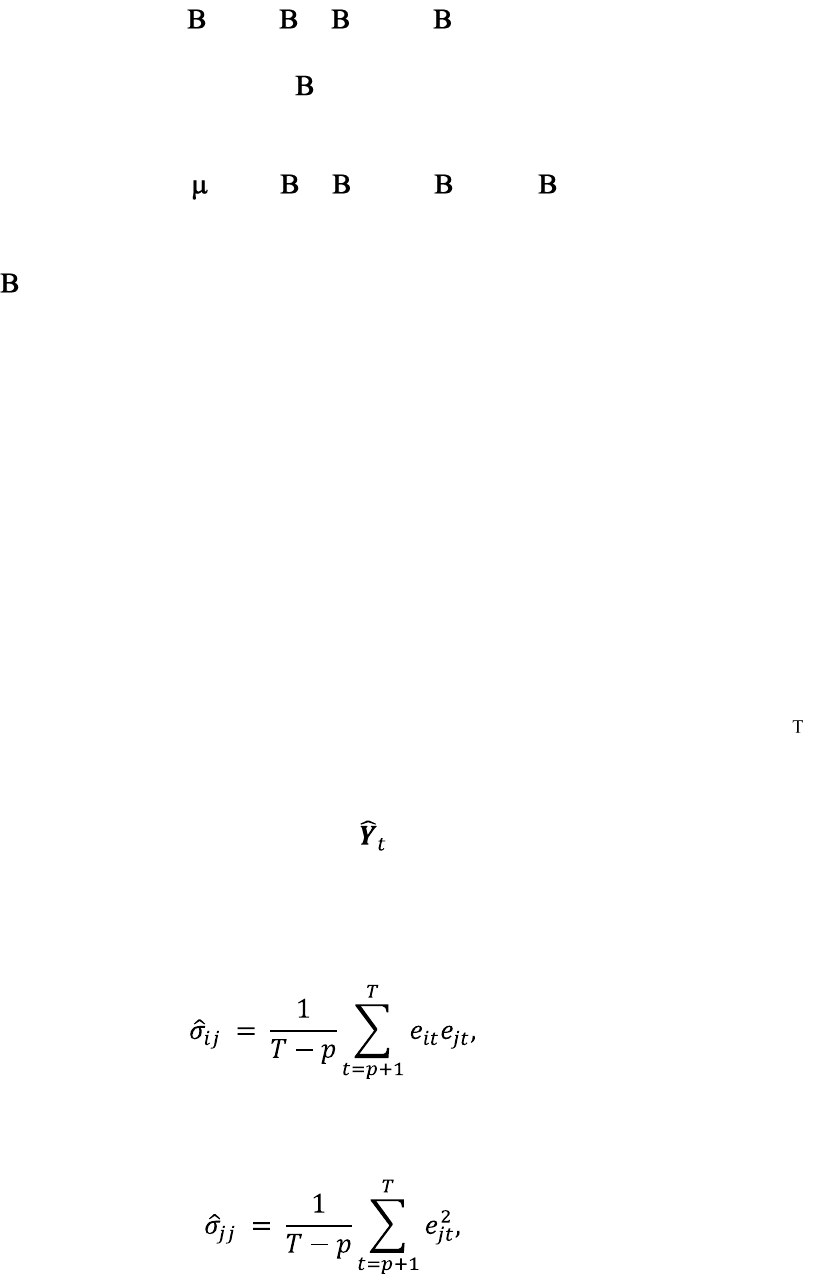
которые используем для оценки элементов ковариационно матрицы
возмущений для i ≠ j:
и для i = j:
или ковариационной матрицы в целом:

9
Использование модели в приведѐнной форме позволяет проводить
оценивание параметров напрямую, на основе исходных наблюдений.
Если возмущения модели (4.7) распределены по нормальному закону,
то оценки системы параметров, полученные методом наименьших квадратов,
совпадают с оценками, которые можно получить методом наибольшего
правдоподобия. Среди других методов, применение которых для оценки
модели (4.7) возможно, предлагают метод инструментальных переменных
(instrumental variables, IV) и обобщѐнный метод моментов (generalized method
of moments, GMM), по сравнению с которыми оценки метода наименьших
квадратов являются эффективными. Оценивание методом наименьших
квадратов остаѐтся эффективным в классе GMM оценок даже в случае, если
нет оснований предполагать нормальность распределения возмущений
модели.
Структурные параметры могут быть вычислены на основе
приведѐнных, используя следующие соотношения:
j
=
j
; = α; (4.15)
ковариационная матрица ошибок модели в структурной форме может быть
определена как:
= .
В качестве используют оценку, полученную, например, на основе (4.14), и
еѐ разложение, которое называют разложением Холецкого:
= ,
в разложении - матрица размерности k × k с положительными элементами
на главной диагонали, внедиагональные элементы приравниваются к нулю.
даѐт оценку ковариационной матрицы возмущений модели в структурной
форме;
-1
даѐт оценку :
=
-1
.
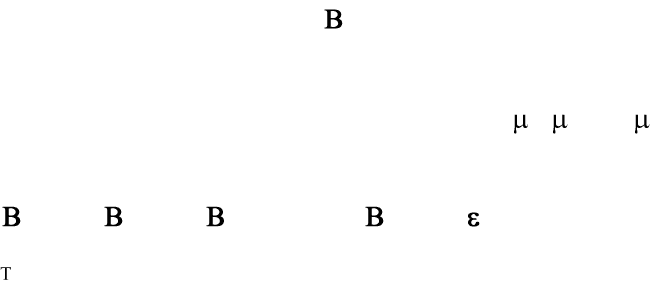
Существует возможность использовать метод наименьших квадратов
для оценки рекурсивных систем векторной авторегрессии. Для этого
10
необходимо отсутствие автокорреляции возмущений. Некоррелированность
возмущений модели и особенности рекурсивных взаимосвязей гарантируют
некоррелированность совместно зависимых переменных возмущениями в тех
уравнениях, в которых совместно зависимые переменные играют роль
объясняющих. Тем самым гарантируется выполнение требований МНК и
состоятельность получаемых оценок.
Для оценивания векторной модели авторегрессии-скользящего среднего
необходимо реализовать более сложную методику. Слагаемые типа
скользящего среднего в VARMA модели оценивают методом наибольшего
правдоподобия. Элементы процессов скользящего среднего аппроксимируют
с помощью авторегрессии достаточно высокого порядка, в идеале подойдет
AR(∞). Приѐм предназначен для устранения актокорреляции в возмущениях
модели.
4.3. Прогнозирование на основе векторной авторегрессии
В нижеследующем изложении будем предполагать, что временные
ряды Y
1t
, Y
2t
, …, Y
kt
стационарны, а матрица обратима. Для удобства
получения дальнейших результатов проведѐм центрирование временных
рядов. Определим y
1t
, y
2t
, …, y
kt
как отклонение наблюдаемых значений
временных рядов Y
1t
, Y
2t
, …, Y
kt
от их математического ожидания
1
,
2
, …,
k
.
В новых обозначениях модель запишем как
y
t
=
1
y
t-1
+
2
y
t-2
+
3
y
t-3
+ … +
p
y
t-p
+
t
, (4.16)
где y
t
= (y
1t
, y
2t
, …, y
kt
) .
Проведѐнное преобразование никак не повлияет на результаты
прогнозирования.
Получение прогнозных оценок значений временных рядов на момент
времени, выходящий за пределы интервала наблюдений, сводится к
рекурсивным вычислениям прогнозных значений на момент y
T+1
, y
T+2
, y
T+3
и
так далее. Информационным множеством для получения прогноза на момент
y
T+1
выступают наблюдения y
T
, y
T-1
, …, y
T-p+1
; базой для прогноза на момент
y
T+2
выступают наблюдения y
T
, y
T-1
, …, y
T-p+2
и прогноз на y
T+1
соответственно.
Тем не менее, при построении прогнозов мы будем считать, что опираемся на
всю предшествующую информацию I
T
= {y
T
, y
T-1
, … }, где символ I
T
означает
всю доступную информацию на момент времени T, на основе которой будет
построен прогноз. Этот прием более удобен при построении выкладок, но не
повлияет на выводы.
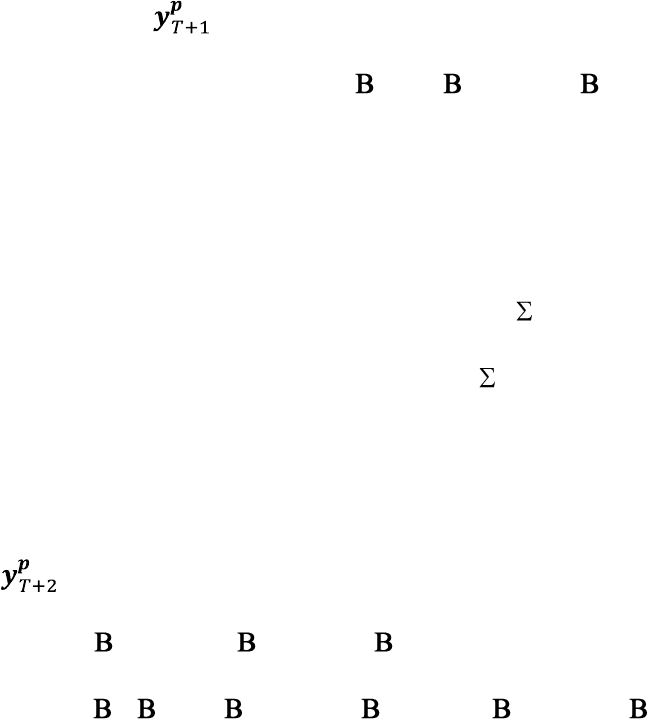
На данном этапе будем предполагать, что нам известны истинные
значения параметром модели. Оптимальный прогноз поведения модели
11
векторной авторегрессии y
T+1
можно получить как условное ожидание y
T+1
относительно информации на момент T:
=
y
T+1
| I
T
= E[y
T+1
| y
T
, y
T-1
, …]
=
1
y
T
+
2
y
T-1
… +
p
y
T-p+1
(4.17)
Ошибка прогноза d
s
определяется как
d
s
= y
T+1
- y
T+1
| I
T
= y
T+1
- E[y
T+1
| y
T
, y
T-1
, …] (4.18)
Нетрудно убедиться, что ковариационная матрица ошибки прогноза модели
векторной авторегрессии на один период вперѐд равна :
cov[y
T+1
| y
T
, y
T-1
, …] = . (4.19)
Для всех последующих моментов времени рекуррентная формула получения
прогнозов поведения модели векторной авторегресии принимает следующий
вид:
=
y
T+2
| I
T
= E[y
T+2
| y
T
, y
T-1
, …]
=
1
y
T+1
| I
T
+
2
y
T-1
… +
p
y
T-p+2
=
1
(
1
y
T
+
2
y
T-1
… +
p
y
T-p+1
) +
2
y
T-1
… +
p
y
T-p+2
(4.20)
4.4. Преимущества и проблемы использования VAR
Преимущественной сферой применения векторной авторегрессии
являются макроэкономические исследования. Модели векторной
авторегрессии обладают хорошими прогностическими свойствами по
сравнению с обычными системами одновременных уравнений в структурной
форме.
Ряд преимуществ дает совместное рассмотрение поведения смешанных
процессов авторегрессии – скользящего среднего, среди которых выделяют
следующие:
1) возможность сократить количество исследуемых лагов;
2) расширение количества анализируемой информации за счѐт
использования данных относительно поведения других переменных;
3) как следствие, получение более надѐжных прогнозов.

12
С точки зрения преимуществ использования векторной авторегрессии
по сравнению с системами одновременных уравнений выдвигают следующие
аргументы:
а) отсутствуют экзогенные переменные;
б) использование в анализе только эндогенных переменных устраняет
необходимость выдвижения априорных ограничений на параметры системы.
Надо иметь в виду, что ограничения на параметры модели, вводимые с целью
обеспечения условий идентифицируемости системы одновременных
уравнений, могут быть в достаточной степени произвольными и
экономически не обоснованными;
в) приведѐнная форма модели векторной авторегрессии, как и
приведѐнная форма системы одновременных уравнений, всегда
идентифицируема.
К основным проблемам применения модели векторной авторегрессии
можно отнести следующую. В эмпирических исследованиях одной из
серьѐзных задач является определение глубины запаздывания реакции
совместно зависимых переменных и соответственно наибольшей длины
временного лага, учтѐнного в модели. Решению проблемы не помогают
использование даже таких инструментов, как автокорреляционный анализ
отдельных временных рядов или частные автокорреляционные функции. Так
как они не вскрывают особенности совместного поведения
автокорреляционных процессов.
Один из общепризнанных подходов к решению задачи определения
глубины запаздывания предусматривает следующие шаги.
1. Оценивание модели векторной авторегрессии для разных значений
временного лага p.
2. Применение для обоснования выбора глубины запаздывания
информационных критериев, таких как критерий Шварца или
критерий Акайке.
Другой подход на первом этапе также предполагает проведение оценки
модели. Оцениванию подлежит модель с наибольшим временным лагом
запаздывания. К оценѐнной модели применяют статистические критерии для
оценки значимости параметров.
4.5. Mодель векторного скользящего среднего
Взаимосвязь моделей векторной авторегрессии и векторного
скользящего среднего. Mодель векторного скользящего среднего (vector
moving average model или VMA) легко получить из модели векторной
авторегрессии. Для этого достаточно вернуться к представлению VAR в виде
(4.10). Если (L) обратима, то мы можем умножить выражение (4.10) слева на
(L)
-1
в результате получим:
13
Y
t
= (L)
-1
α + (L)
-1
t
, (4.21)
с учетом (4.13)
Y
t
= + (L)
-1
t
, (4.22)
Из (4.21) видим, что каждый элемент вектора Y
t
можно представить как
взвешенную сумму всех текущих и предшествующих возмущений в модели.
В концепции анализа функций импульсной отдачи элементы этих
возмущений именуются шоками. Представив (L)
-1
как
(L)
-1
= I
k
+ A
1
L + A
2
L
2
+ …, (4.23)
где, как и в (4.9), L
s
– оператор запаздывания (лаговый оператор), A
s
– матицы
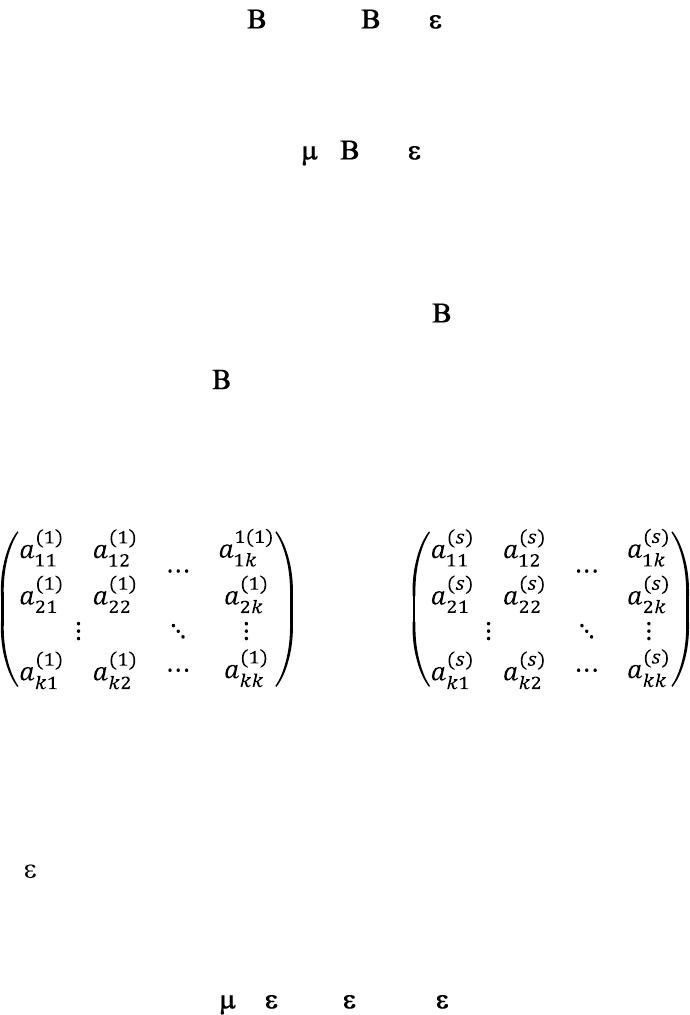
соответствующих параметров размерности k×k:
A
1
= ; …; A
s
= ; … .
Элементы матрицы a
ij
соответствуют параметрам модели векторного
скользящего среднего, первый индекс указывает на принадлежность к i-му
уравнению, второй индекс привязан к случайной составляющей j-й
переменной
jt
, стоящей в уравнении с лагом s.
Используя (4.23) мы получим развѐрнутую запись векторной модели
скользящего среднего как
Y
t
= +
t
+ A
1 t -1
+ A
2 t -2
+ … . (4.24)
Представление (4.24) называют моделью бесконечного векторного
скользящего среднего или представлением Вольда.
Проблема стационарности векторной авторегрессии. Условием
сходимости Y
t
будет приближение последовательности матриц A
s
к нулевой
матрице по мере стремление s к бесконечности: s → ∞. Требование
сходимости A
s
гарантирует постепенное затухание всех последующих членов
ряда Y
s
.
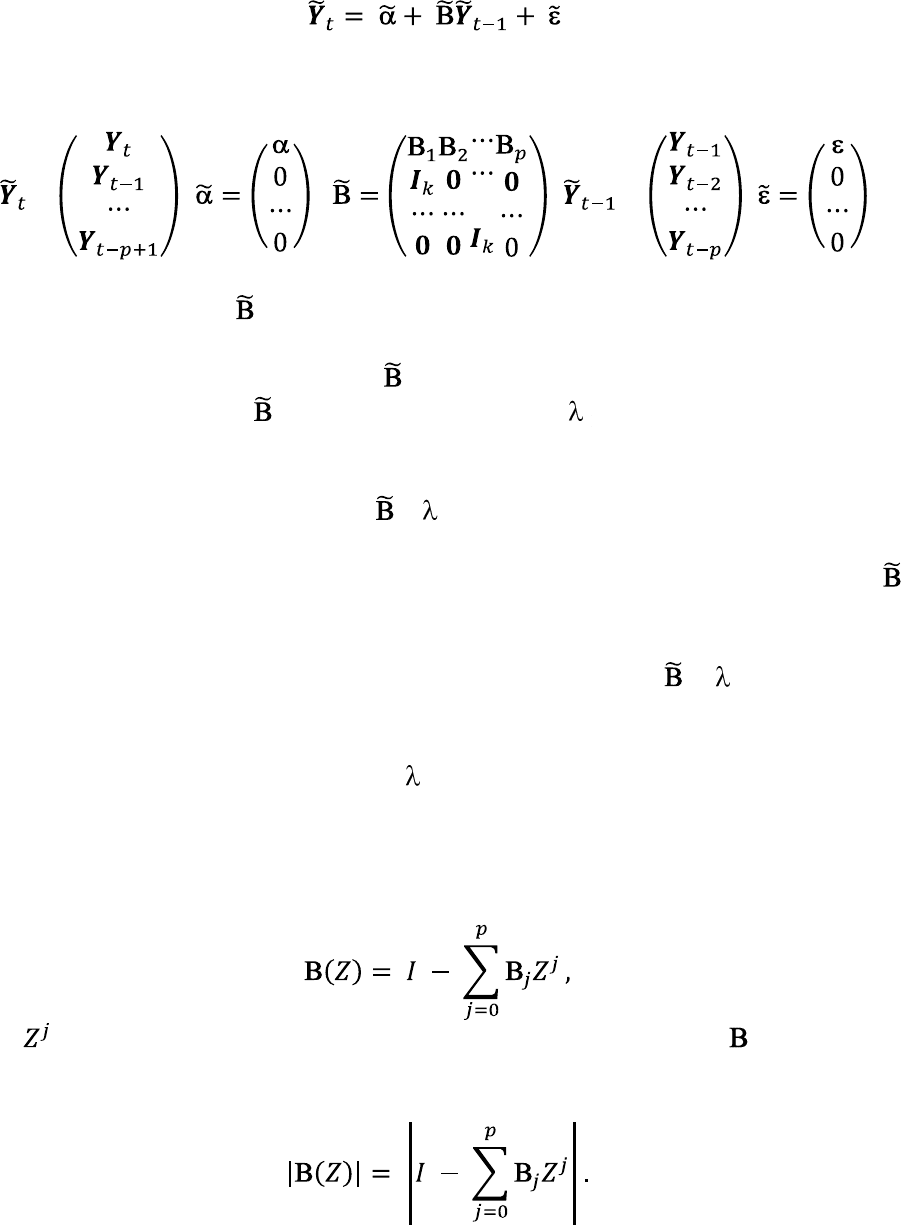
14
Возвращаясь к обсуждению вопросов сходимости на основе анализа
единичных корней для случая векторной авторегрессии, в начале перепишем
модель векторной авторегрессии (4.7) как VAR первого порядка:
,
где
= ; ; = .
Размерность матрицы равна (k ∙ p)× (k ∙ p).
Для сходимости последовательности Y
s
при s→∞ необходимо, чтобы
собственные значения матрицы лежали внутри единичного круга. По
определению матрицы собственные значения гарантируют выполнение
следующего условия
| – I| = 0,
где I – единичная матрица, размерность которой совпадает с размерностью ,
то есть равна dim (I) = (k ∙ p)× (k ∙ p).
Процесс векторной авторегрессии VAR(p) стационарен в широком
смысле, если абсолютные значения корней уравнения | - I| = 0 меньше
единицы:
| | < 1.
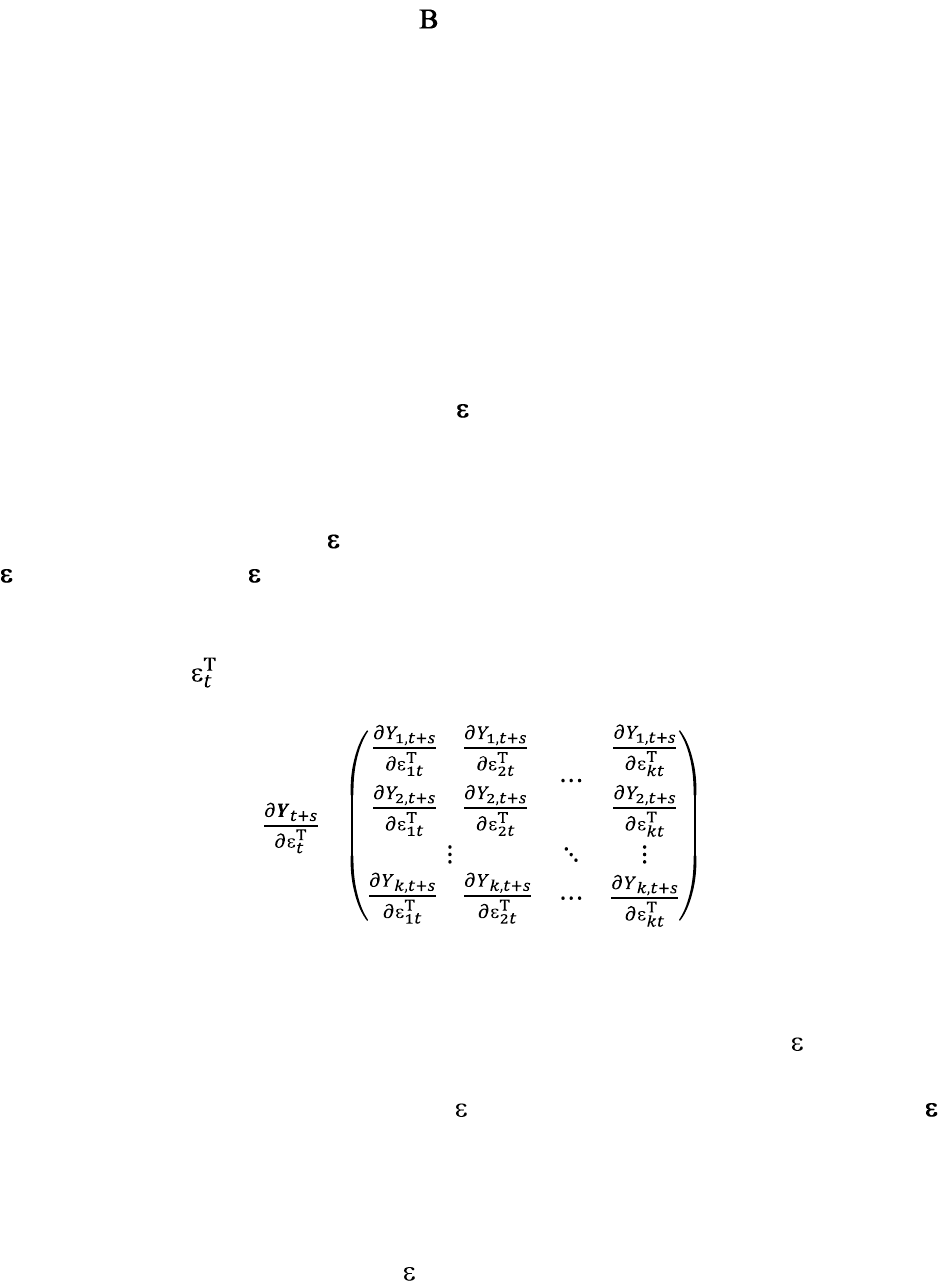
Условие (4.52) можно записать, используя матричный характеристический
многочлен:
где – собственные векторы. Определитель матрицы (Z) является
скалярным характеристическим многочленом:
15
Потому характеристическое уравнение принимает вид:
| (Z)| = 0.
Условие стационарности будет состоять в том, что корни
характеристического уравнения должны лежать за пределами единичного
круга.
4.6. Функция импульсной отдачи
Для обсуждения вопросов анализа импульсно отдачи вернѐмся к
представлению модели в виде векторной модели скользящего среднего (4.24).
Будем предполагать, что:
1) вектор возмущений модели
t
имеет распределение по типу белого
шума;
2) возмущения разных уравнений модели взаимно не коррелированы.
Пусть вектор d с ненулевыми значениями элементов имеет такую же
размерность, как и вектор
t
. Предположим, мы добавили вектор d к вектору
t
. Учитывая, что E[
t
]=0, элементы вектора d вносят в систему возмущения
или шоки. Каков эффект в Y
t + s
под влиянием шоков мы получим через s
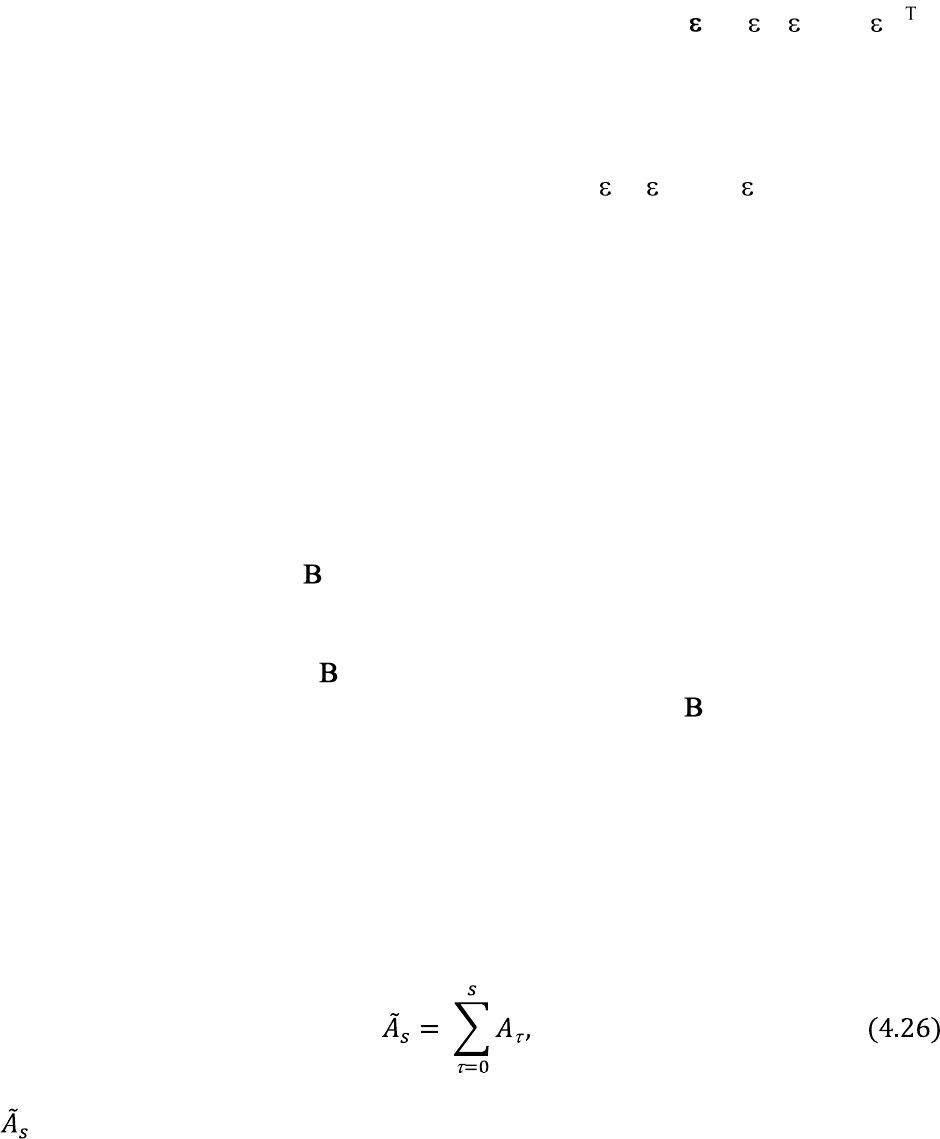
периодов? Ответ на этот вопрос мы можем получить, определив производную
вектора Y
t + s
по , тем самым мы найдем параметры матрицы A
s
:
A
s
= = . (4.25)
Учитывая (4.25), вернѐмся к интерпретации матрицы A
s
. Элемент матрицы A
s
с координатами (i,j) показывает, на какую величину изменится значение
временного ряда Y
j,t+s
в момент времени (t+s) при изменении
it
в момент
времени t на единицу. Предположим, к примеру, что шоки возникают в
возмущениях переменной j, то есть в
jt
, а остальные составляющие вектора
t
не изменились. Тогда по истечении периода s эффекты от шоков в
переменных Y
1,t+s
, Y
2,t+s
, …, Y
k,t+s
мы обнаружим только в j-м столбце
соответствующих матриц A
1
, A
2
, … , A
s
… . Все остальные столбцы матриц
A
1
, A
2
, … , A
s
… останутся нулевыми.
Если эффекты от шоков в
jt
в момент времени t находят отражение в
изменении лишь одной переменной Y
i,t+s
в момент времени (t+s) то эффекты
16
от такого увеличения можно будет найти через элементы i-й строки j-го
столбца матриц A
1
, A
2
, …, A
s
… .
Наконец, если шокам подвержены все возмущения
t
= (
1t
,
2t
, …,
kt
) , а
динамические эффекты возникают во всех совместно зависимых переменных
Y
1,t+s
, Y
2,t+s
, …, Y
k,t+s
, тогда мы будем иметь дело с матрицами A
1
, A
2
, …, A
s
… ,
все элементы которых будут ненулевыми.
Так как наблюдаемыми величинами являются совместно зависимые
переменные Y
1,t
, Y
2,t
, …, Y
k,t
, а не возмущения
1t
,
2t
, …,
kt
, то элементы
матриц A
1
, A
2
, …, A
s
… фактически демонстрируют отклик в Y
1,t+s
, Y
2,t+s
, …,
Y
k,t+s
на импульсы, возникающие в Y
1,t
, Y
2,t
, …, Y
k,t
, при условии что все другие
переменные на момент времени t и ранее остаются постоянными
Функция импульсной отдачи (impulse-response function, IRF)
представляет собой графическое представление элементов матриц I
k
, A
1
, A
2
,
…, A
s
… как функции временного лага или глубина запаздывания s.
Исследование функций импульсной отдачи представляет большой интерес, в
том числе с помощью графического инструментария, и находит в некоторых
областях финансового и экономического анализа достаточно широкое
применение.
Как видно из (4.22), для построения функции импульсной отдачи
необходимо определить (L)
-1
,
что является делом достаточно сложным. Но
можно пойти другим путѐм и воспользоваться имитационными методами.
Другой проблемой анализа функций импульсной отдачи является
вырожденность матрицы (L) и, как следствие, невозможность определить
обратную матрицу. Одной из причин вырожденности (L) может являться
отсутствие стационарности во временных рядах Y
1,t
, Y
2,t
, …, Y
k,t
. Подчеркнѐм
ещѐ раз, что возможность представления векторной авторегрессии в виде
модели векторного скользящего среднего появляется при условии
стационарности всех временных рядов, образующих вектор Y
t
. Речь идет о
стационарности типа I(0).
Рассмотрим другой показатель накопленной реакции на импульсы,
который можно определить как:
характеризует суммарную величину запаздывания влияния шоков на
совместно зависимые переменные на глубину запаздывания от нуля до s.
Влияние шоков на бесконечном периоде запаздывания демонстрирует
матрица F:
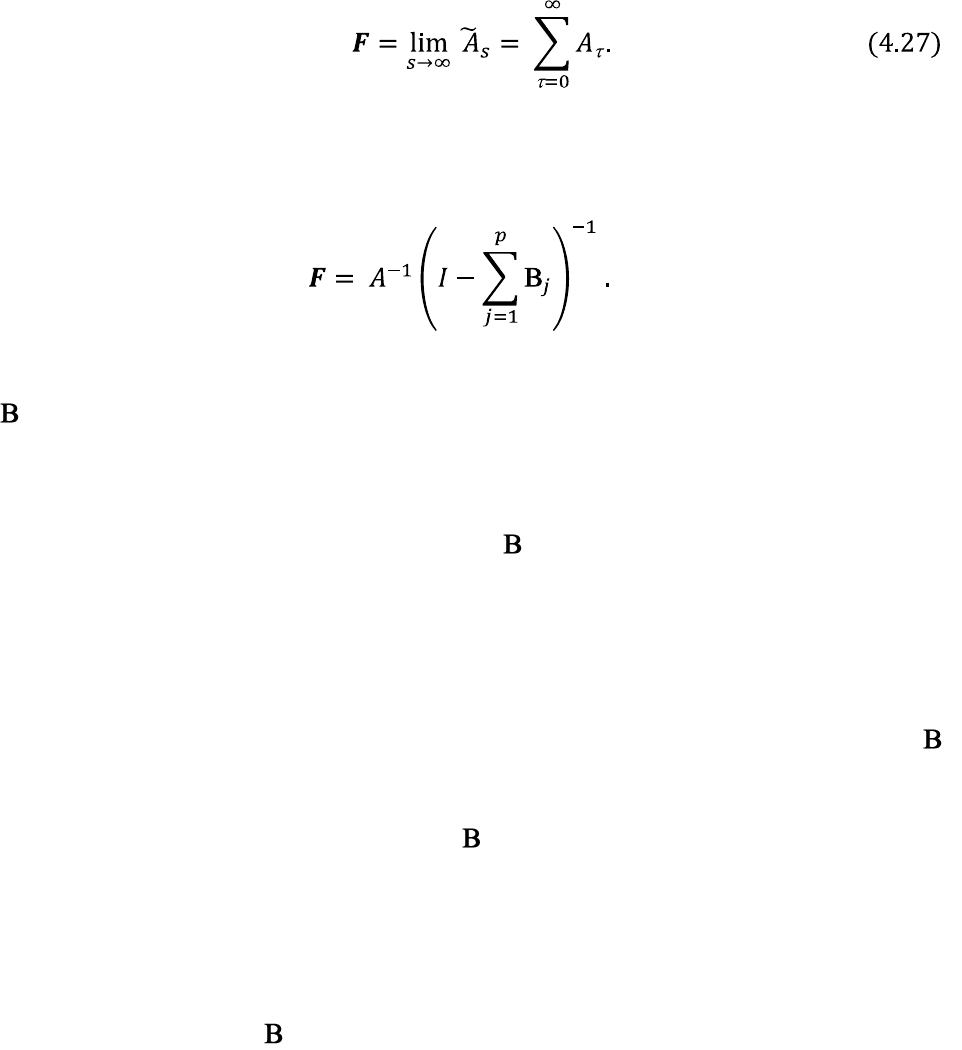
17
Матрицу F называют долгосрочным мультипликатором и аппроксимируют
через
Можно выделить несколько частных случает вырожденности матрицы
(L). Все они связаны с отсутствием стационарности во временных рядах.
1. В структуре хотя бы одной совместно зависимой переменной из Y
t
,
присутствует стохастический тренд. Следовательно, имеет место
интегрированный временной ряд порядка один I(1), для которого существуют
единичные корни, поэтому ранг матрицы будет равен (k – 1).
2. В другом крайнем случае мы можем иметь k стохастических
независимых тренда в структуре временных рядов, то есть все k переменных
Y
1,t
, Y
2,t
, …, Y
k,t
выступают как интегрированные процессы первого порядка
I(1) или процессы с единичным корнем. Независимость трендов гарантирует
нам отсутствие коинтеграции временных рядов. В случае присутствия k
стохастических независимых трендов в структуре временных рядов
является нулевой матрицей:
rank( ) = 0.
3. Промежуточная ситуация будет иметь место, когда часть
временных рядов из Y
1,t
, Y
2,t
, …, Y
k,t
коинтегрированы, то есть включают
стохастические тренды и является интегрированными первого порядка
рядами, а остальные временные ряды стохастический тренд не включают.
Тогда ранг матрицы (L) будет совпадать с числом линейных комбинаций
переменных из Y
t
, стационарных типа I(0), которые образуют набор
коинтегрированных векторов.
Третий случай представляет наибольший интерес для анализа.
4.7. Особенности коинтеграции в векторной авторегрессии
Выделим основные проблемы анализа процессов коинтеграции,
возникающие при изучении векторной авторегрессии.
