Суслов В.И., Лапо В.Ф., Талышева Л.П., Ибрагимов Н.М. Эконометрия-3
Подождите немного. Документ загружается.

Рекомендуемая литература
91
4. Dickey, D.A. and Fuller W.A. Di stributions of the Estimators
for Autoregressive Time Series With a Unit Root // Journal of
American Statistical Association, 1979, No. 75, p. 427–431.
5. Enders W. Applied Econometric Time Series. — John Wiley &
Sons, 1995.
6. Engle R.F. and Granger C.W.J., Co-integration and Error
Correction: Representation, Estimation and Testing // Econometrica,
1987, No. 55, p. 251–276.
7. Granger C.W.J., and Newbold P. Spurious Regressions in
Econometrics // Journal of Econometrics, 1974, No. 21, p. 111–
120.
8. Greene W.H. Econometric Analysis. — Prentice-Hall, 2000. (Ch.
18, p. 776–784.)
9. Said, E.S. and Dickey D.A. Testing for Unit Roots in Autoregressive-
Moving Average Models of Unknown Order. // Biometrica,
1984, No. 71, p. 599–607.
92
Интегрированные процессы. . .
10. Stock, J.H. and Watson M.W. Testing for Common Trends //
Journal of the American Statistical Association, 1988, No. 83,
p. 1097–1107.
11. Stock, J.H. Asymptotic Properties of Least Squares Estimators
of Cointegrating Vectors // Econometrica, 1987 , No. 55, p.
1035–1056.
12. Wooldridge Jeffrey M. Introductory Ec onometrics: A Modern
Approach. — 2nd ed. — Thomson, 2003. (Ch. 18.)
Глава 4.
Вект орная авторегрессия
93

1
4. Векторная авторегрессия
4.1. Основные понятия векторной авторегрессии
Модели векторной авторегрессии (vector autoregressive model, или
сокращенной VAR) с одной стороны, являются обобщением,
авторегрессионных моделей для случая многомерных временных рядов. А с
другой стороны, модель векторной авторегрессии является частным случаем
системы одновременных уравнений. Переменные, поведение которых во
времени подлежит моделированию, в рамках векторной авторегрессии
образуют многомерный временной ряд. Предполагается, что многомерные
временные ряды, составляющие вектор переменных, генерирует некоторый
стохастический процесс. Таким образом, модель векторной авторегрессии
должна описывать совместную эволюцию переменных во времени, опираясь
на информацию, которую содержат сами временные ряды.
Наиболее простое определение, которое можно дать модели векторной
авторегресии, следующее: это эконометрическая модель, которая
одновременно описывает поведение нескольких совместно зависимых
переменных через изменение собственных предшествующих значений и
значений других совместно зависимых переменных.
Приведѐм в качестве примера самый простой случай векторной
авторегрессии. Рассмотрим поведение двух переменных. Модель будет
учитывать авторегрессию первого порядка. Обозначим изучаемые совместно
зависимые переменные как X
t
и Y
t
, где t – индекс времени. Учитывая наши
предположения, модель будет включать два уравнения. В уравнение для
каждой из двух совместно зависимых переменных, как для X
t
, так и для Y
t
,
входят авторегрессионные составляющие первого порядка X
t-1
и Y
t-1
. Таким
образом, мы получим следующую систему одновременных уравнений,
которую, в нашем случае, мы вправе назвать векторной авторегрессией
первого порядка:
X
t
=
1
+ β
11
X
t-1
+ β
12
Y
t-1
+
1t
(4.1)
Y
t
=
2
+ β
21
X
t-1
+ β
22
Y
t-1
+
2t
, (4.2)
где
1
, β
11
, β
12
,
2
, β
21
, β
22
– параметры. Первый индекс для параметров
указывает на уравнение, второй индекс - на переменную. Так индексы при β
12
говорят, что параметр входит в состав первого уравнения стоит при
предшествующих значениях зависимой переменной Y
t-1
. Возмущения модели
для первого и второго уравнения обозначены как
1t
и
2t
соответственно и
представляют собой процессы типа белого шума с соответствующими
параметрами распределения:
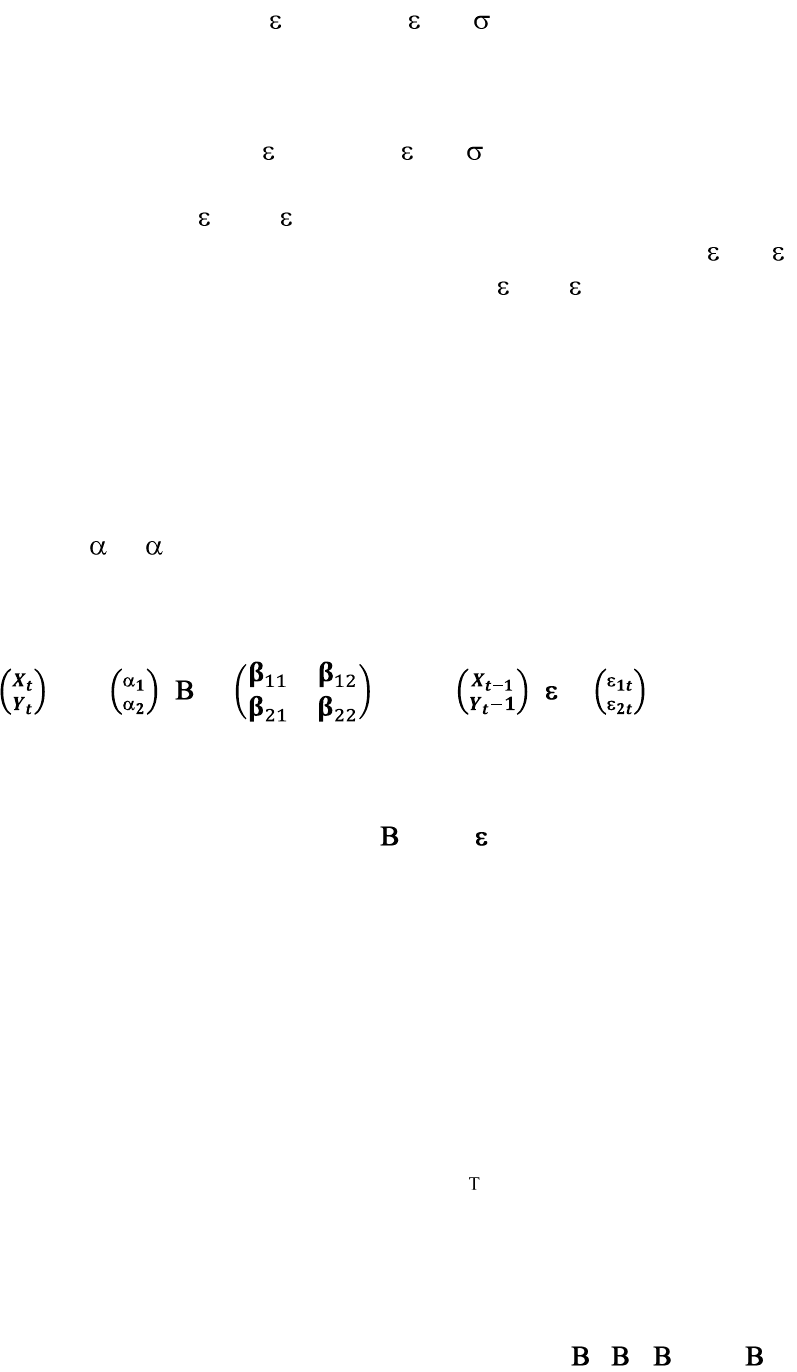
2
E[
1t
] = 0, var[
1t
] =
2
(4.3)
и
E[
2t
] = 0, var[
1t
] =
2
, (4.4)
будем предполагать, что
1t
и
2t
не коррелируют между собой вне
зависимости от поведения X
t
и Y
t
, хотя, в общем случае, процессы
1t
и
2t
могут коррелировать. Распределение возмущений
1t
и
2t
не зависит от
распределения исследуемых зависимых переменных X
t
и Y
t
.
Интерпретация параметров векторной авторегрессии определяется
структурой уравнений. Так ненулевое значение параметра β
11
говорит о
наличии процессов автокорреляции в X
t
, а ненулевое значение параметра β
12
означает, что предшествующие значения Y
t-1
оказывают значимое влияние на
процесс формирования переменной X
t
,. Аналогичную интерпретацию в
отношении процесса, представленного в Y
t
, имеют параметры β
21
и β
22
во
втором уравнении;
1
и
2
– константы.
Запишем систему уравнений (4.1) – (4.2) в матричном виде. Введѐм
обозначения. Пусть
Y
t
= ; α = ;
1
= ; Y
t-1
= ;
t
= , (4.5)
тогда с учѐтом (4.5) система принимает вид
Y
t
= α +
1
Y
t-1
+
t
, (4.6)
которую в дальнейшем будем обозначать как VAR(1).
Введѐнные обозначения позволяют легко обобщить матричную запись
модели авторегрессии первого порядка VAR(1) с двумя совместно
зависимыми переменными на случай авторегрессии более высокого порядка и
размерности. Пусть p – порядок авторегрессии, k – количество совместно
зависимых переменных, k определяет размерность вектора Y
t
, тогда вектор
совместно зависимых переменных будет включать k совместно зависимых
переменных:
Y
t
= (Y
1t
, Y
2t
, …, Y
kt
) .
Кроме того, введѐм векторы отставания значений совместно зависимых
переменных Y
t-1
, Y
t-2
,…, Y
t–p
соответственно с лагом запаздывания 1, 2, …, p;
размерность векторов Y
t-1
, Y
t-2
,…, Y
t–p
равна k. Обозначим через α – вектор
параметров свободных членов уравнений размерности k;
1
2
,
3
, …,
p
–
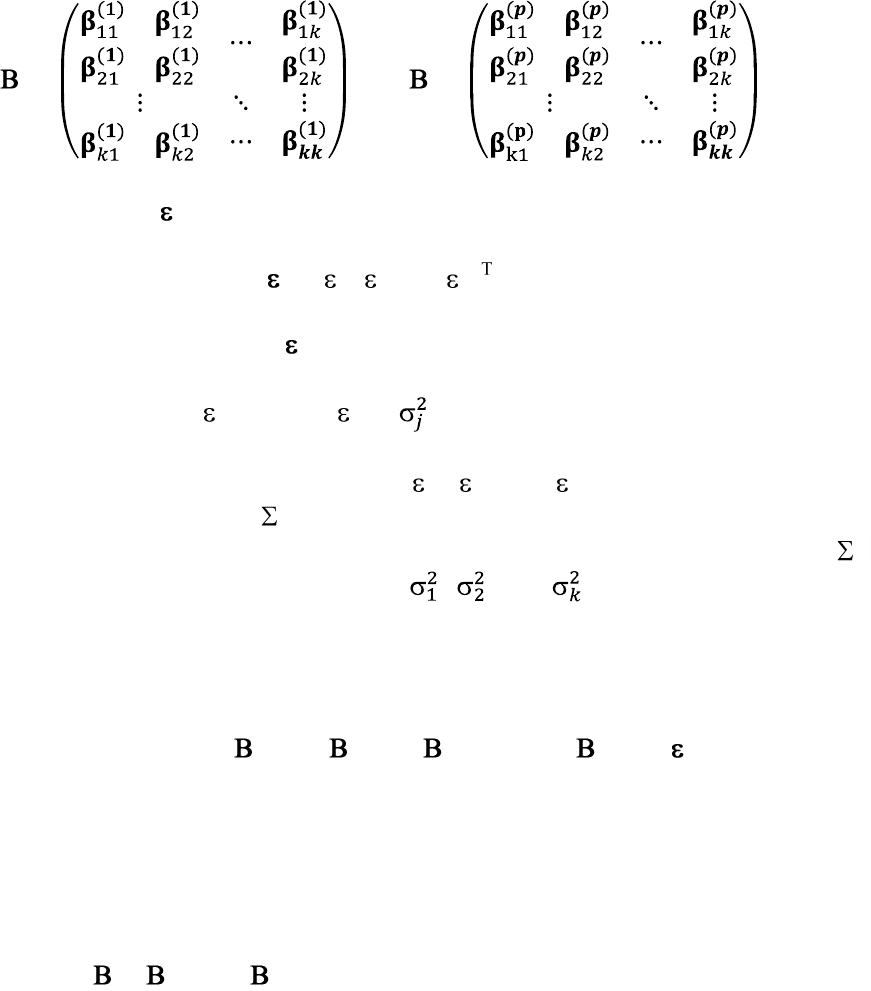
3
матицы параметров размерности k×k, соответствующие векторам
лагированных значений переменных Y
t-1
, Y
t-2
,…, Y
t–p
соответственно:
1
= ; …;
p
= .
Вектор возмущений
t
также будет иметь размерность, равную k:
t
= (
1t
,
2t
, …,
kt
) .
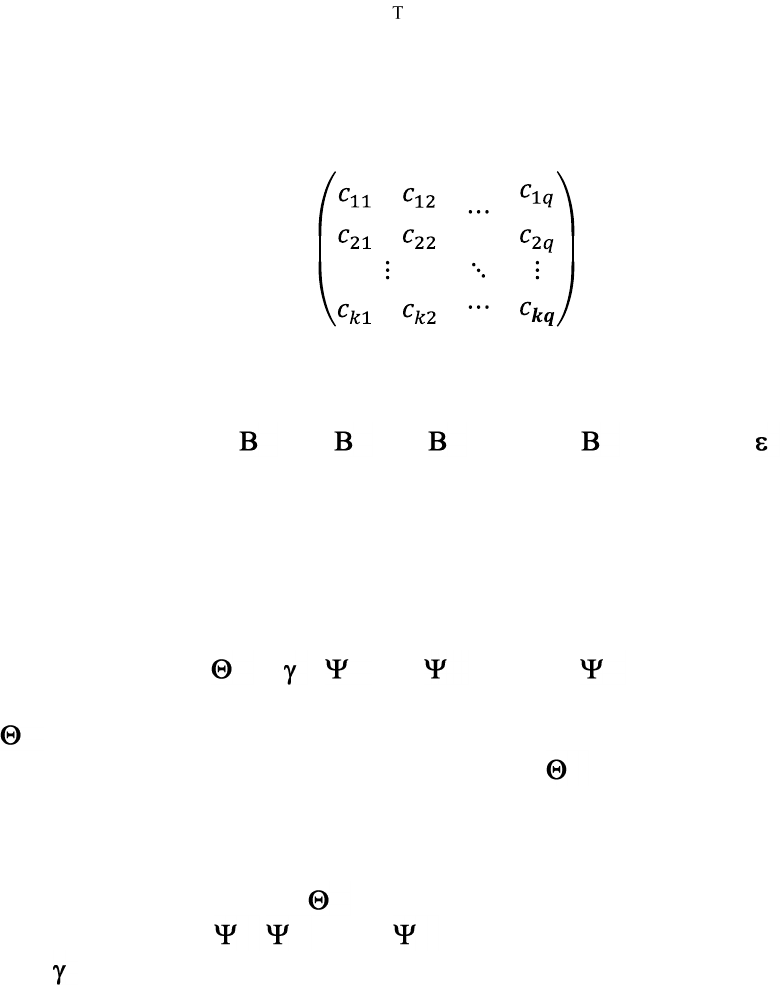
Распределение членов вектора
t
характеризуется как белый шум:
E[
jt
] = 0, var[
jt
] = , j = 1, 2, … k.
Ковариационную матрицу возмущений
1t
,
2t
, …,
kt
для любого момента
времени t обозначим как , размерность матрицы составляет k×k. При
выполнении предположения о некоррелированности возмущений матрица
имеет диагональный вид с элементами , , …, , расположенными на
главной диагонали.
Тогда модель векторной авторегресии порядка p, которую принято
обозначать как VAR(p), запишем в следующем виде
Y
t
= α +
1
Y
t-1
+
2
Y
t-2
+
3
Y
t-3
+ … +
p
Y
t-p
+
t
, (4.7)
Как известно, выделяют системы уравнений в структурной и
приведѐнной форме. Запись векторной авторегрессии в форме (4.1)-(4.2) или в
(4.7) можно рассматривать как аналог приведѐнной формы записи систем
одновременных уравнений, так как совместно зависимые переменные не
используются справа в уравнениях в качестве объясняющих переменных.
Параметры α,
1
,
2
, …,
p
в (4.7) являются приведѐнными параметрами.
Проводя другие параллели с системами одновременных уравнений, отметим,
что все переменные в модели Y
1t
, Y
2t
, …, Y
kt
, характеризующие текущее
состояние процессов, играют роль совместно зависимых переменных.
Переменные с запаздыванием Y
t-1
, Y
t-2
, …, Y
t-p
выступают как
предопределѐнные и берут на себя функцию объяснения динамики зависимых
переменных. Отметим, что в векторной авторегрессии все переменные
определяются внутри системы, то есть являются эндогенными. Вместе с тем,
наличие переменных с запаздыванием Y
t-1
, Y
t-2
, …, Y
t-p
позволяет
характеризовать модель (4.7) как динамическую модель.
4
Система уравнений (4.7) представляет собой исходный или
традиционный вариант модели векторной авторегрессии. В традиционном
варианте модели нет экзогенных переменных, они не выступают в роли
объясняющих переменных. Не выступают в роли объясняющих и совместно
зависимые переменные Y
1t
, Y
2t
, …, Y
kt
. Поведение всех совместно зависимых
переменных объясняется через влияние с запаздыванием со стороны самих
эндогенных переменных Y
1t
, Y
2t
, …, Y
k
. Важно понимать эту особенность
векторной авторегрессии.
Тем не менее, модель допускает включение экзогенных переменных в
качестве объясняющих. Это может быть сделано, например, следующим
образом. Пусть X
t
, = (X
1t
, X
2t
, …, X
qt
) – вектор текущих или предшествующих
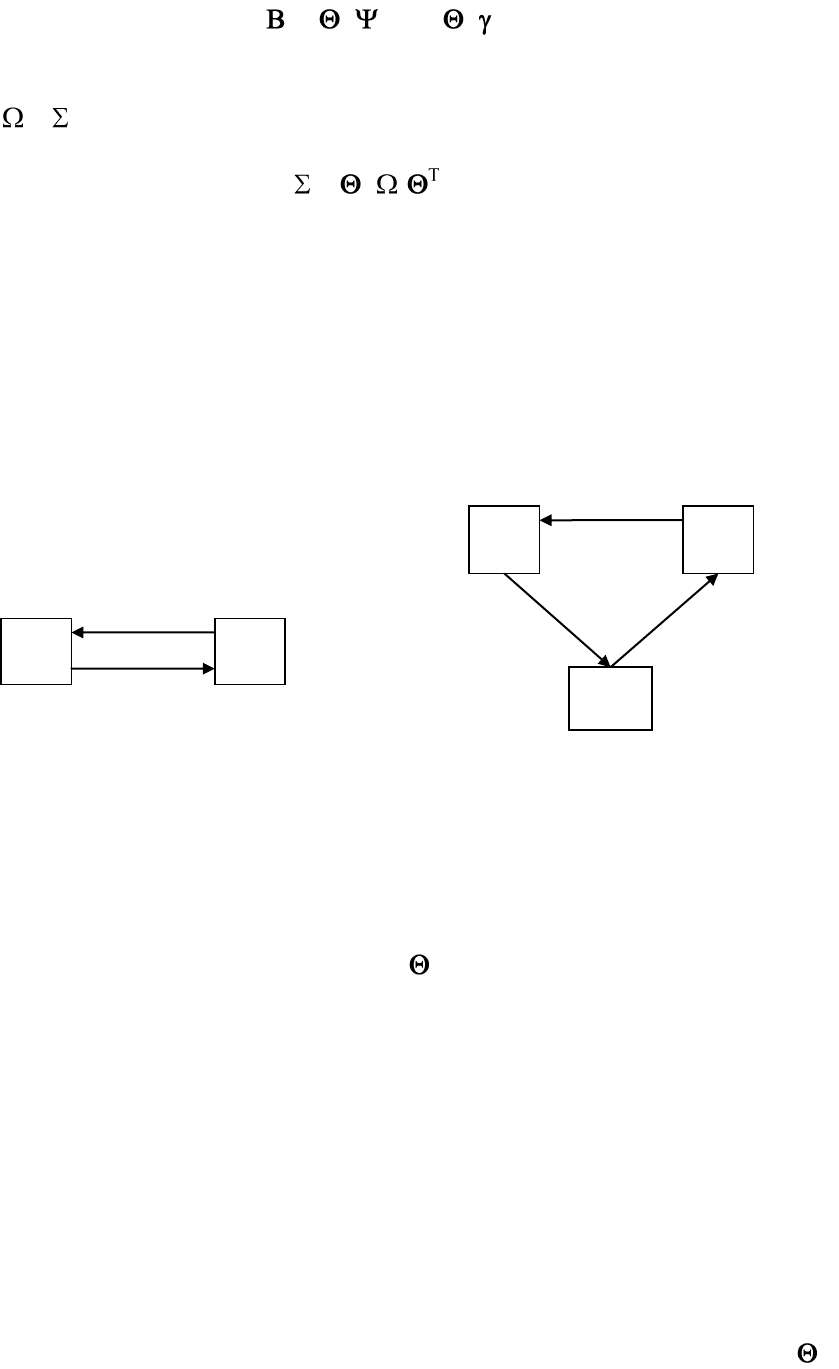
моменту t значений экзогенных переменных, всего q переменных; С –
матрица параметров размерности k×q; соответствующая вектору экзогенных
переменных:
С = .
Тогда модель с экзогенными переменными она принимает следующий вид:
Y
t
= α +
1
Y
t-1
+
2
Y
t-2
+
3
Y
t-3
+ … +
p
Y
t-p
+ СX
t
, +
t
.
В качестве экзогенной переменной может выступать, например,
переменная времени t, отражающая при необходимости временной тренд.
Структурная форма записи может быть получена на основе
приведѐнной формы следующим образом:
Y
t
= +
1
Y
t-1
+
2
Y
t-2
+ … +
p
Y
t-p
+ w
t
, (4.8)
где матрица размерности k×k с элементами на главной диагонали, равными
единице. Внедиагональные элементы матрицы в (4.8), при условии, что
совместно зависимые переменные Y
1t
, Y
2t
, …, Y
kt
не выступают в качестве
объясняющих, равны нулю. Но если в модели векторной авторегрессии
текущие значения зависимых переменных Y
1t
, Y
2t
, …, Y
kt
выступают в качестве
объясняющих, то в матрице могут появиться ненулевые внедиагональные
элементы. Матрицы
1
,
2
, … ,
p
имеют размерность k×k. Размерность
вектора равна k. Вектор w
t
включает возмущения в текущий момент времени
t и имеет размерность, равную k. Структурные и приведѐнные параметры
связаны следующими соотношениями:
5
j
=
-1
j
; α =
-1
;
ковариационные матрицы ошибок модели в структурной и приведѐнной
форме, и соответственно, связаны как:
=
-1
( )
-1
.
Чтобы подчеркнуть, что модель векторной авторегрессии записана в
структурной форме с экзогенными переменными, можно использовать такое
общепризнанное обозначение, как SVAR.
Частным случаем системы одновременных уравнений является модель
в рекурсивной форме, когда взаимосвязи между совместно зависимыми
переменными не имеют замкнутых цепей, подобных тем, что приведены на
рис. 4.1.
Рис. 4.1. Схемы замкнутых взаимосвязей совместно зависимых переменных в
системах одновременных уравнений
В рекурсивных системах матрица в представлении модели в форме
(4.8) имеет диагональный вид.
Отметим, что для моделей векторной авторегрессии в структурной
форме возникают те же проблемы, что и для систем одновременных
уравнений в структурной форме. Среди основных – проблема
идентифицируемости параметров. Для идентифицируемости на структурные
параметры должны быть наложены серьѐзные ограничения. Подробно этот
вопрос обсуждался в главе, посвященной системам одновременных
уравнений. Перечислим виды идентифицирующих ограничений, которые
могут быть использованы.
1. Ограничения на параметры одного уравнения. Среди них
выделяют нормирующие ограничения, налагаемые, например, путѐм
приравнивания элемента, стоящего на главной диагонали в матрице , к
Y
1t
Y
2t
Y
3t
Y
1t
Y
2t

6
единице; приравнивание некоторых структурных параметров к нулю;
связывание нескольких структурных параметров одного уравнения общим
условием или тождеством.
2. Ограничения на параметры нескольких структурных уравнений. В
данном пункте можно выделить введение условий, связывающих параметры
нескольких уравнений, и искусственное введение рекурсивной структуры
взаимосвязи совместно зависимых переменных.
3. Ограничение на структуру ковариационной матрицы возмущений
. Например, установление требования диагональности структуры
ковариационной матрицы. Подобное ограничение в моделях векторной
авторегресии является существенными, и называется ограничением
ортогональности возмущений.
Следует подчеркнуть, что все ограничения на параметры должны иметь
под собой серьѐзные основания, и бывают не всегда оправданы с точки
зрения экономики. Необоснованно ведѐнные ограничения приводят к
существенному смещению оценок параметров и значительным искажениям
истинной картины взаимосвязей переменных. По этим причинам в настоящее
время при анализе моделей векторной авторегрессии преимущество отдаѐтся
моделям в приведѐнной форме, которую, как уже упоминалось, называют
исходной или традиционной формой модели.
Дальнейший анализ сосредоточим на моделях, в виде (4.7), которые
включают только эндогенные переменные.
Матричное представление векторной авторегрессии можно записать с
использованием оператора запаздывания (лагового оператор) L , где
величина лага.
Определим матричный полиномиальный оператор
запаздывания (матричный полиномиальный лаговый оператор) (L), как
(L) = I
k
–
1
L –
2
L
2
–
3
L
3
– … –
p
L
p
, (4.9)
где
1
,
2
, …,
p
– матрицы, аналогичные приведѐнным в (4.7); I
k
–
единичная матрица размерности k. Как видим, полиномиальный лаговый
оператор, определѐнный в (4.9), представляет собой матрицу, размерности
k×k; каждое произведение
L , = 1, 2, …, p, тоже является матрицей
размерности k×k. Элементы матрицы (L) формируются как полиномы
порядка p.
Используя матричный полиномиальный оператор запаздывания (4.9)
можем записать модель векторной авторегресии (4.7) в следующем виде:
(L)Y
t
= α +
t
(4.10)
Можно выделить несколько вариантов модели векторной авторегресии,
которые зависят от особенностей распределения возмущений модели
t
.

7
Один из вариантов мы уже описали. Он предполагает распределение
элементов
t
как белый шум. При этом возмущения разных уравнений
1t
,
2t
,
…,
kt
для любого момента времени t могут быть как коррелированы, так и не
коррелированы между собой. В это случае все компоненты векторной
авторегрессии представляют собой одномерные ARMA модели, которые мы
рассматриваем совместно.
Другой известный вариант модели помимо авторегрессионной
составляющей предусматривает включение авторегрессии возмущений и
представляет собой векторный вариант авторегрессионной модели
скользящего среднего (ARMA), которую в англоязычной литературе
обозначают как VARMA. Его легко получить умножением вектора
t
на
матричный полиномиальный оператор запаздывания (L). Однако возникают
существенные проблемы оценивания модели векторной авторегрессии-
скользящего среднего, потому модели типа VARMA не нашли широкого
распространения.
4.2. Вопросы оценивания. Свойства модели и оценок параметров
При дальнейшем рассмотрении векторной авторегрессии будем
предполагать стационарность временных рядов, включѐнных в Y
t
= (Y
1t
, Y
2t
,
…, Y
kt
) . При этом условии математическое ожидание Y
t
не зависит от
времени и будет равно вектору , состоящему из констант:
E[Y
t
] = = (
1
,
2
, …,
k
) .
Найдѐм ожидаемое значение Y
t
исходя из модели (4.7):
E[Y
t
] = α +
1
E[Y
t-1
] +
2
E[Y
t-2
] + … +
p
E[Y
t-p
] + E[
t
] =
=α +
1
E[Y
t
] +
2
E[Y
t
] + … +
p
E[Y
t
]. (4.11)
Перенесѐм в (4.11) все члены с математическим ожиданием влево:
E[Y
t
] -
1
E[Y
t
] -
2
E[Y
t
] - … -
p
E[Y
t
] = α,
тогда, учитывая стационарность временных рядов и, что E[Y
t
] = , получим
-
1
-
2
- … -
p
= (I -
1
-
2
- … -
p
) = α. (4.12)
Матрица в скобах в выражении (4.12) имеет размерность k×k, обозначим еѐ
через :
