Строшио М., Дутта М. Фононы в наноструктурах

Подождите немного. Документ загружается.

§ 1.

Диэлектрические

континуальные

модели

фононое

описывающих

оптические

фононы

полярных

одноосных

средах

[18].

Одноосные

материалы,

такие

как

гексагональные

кристаллы

GaN, AIN,

xAl

хN

решеткой

вюрцита,

имеют

сравнительно

широкие

энер

гетические

зоны

подходят

для

высокотемпературной

электроники

коротковолновых

оптоэлектронных

устройств.

Лаудон

[18]

ввел

модель,

удобную

для вывода

макроскопических

уравнений

для

одноос

ного

полярного

кристалла,

используя

одно

значение

диэлектрической

постоянной,

EII'

направлении,

параллельном

оси

С,

другое

значе

ние,

E-t,

направлении,

перпендикулярном

оси

С.

модели

Лаудона

система

уравнений

Хуан Куня-Борна

записывается

отдельно

для

фононной

моды

UII'

смещения

которой

параллельны

оси

С,

отдельно

для

фононной

моды

U-t,

смещения

которой

перпендикулярны

ей.

Для

n-й

среды

непосредственно

получаем

= -wio,-t,nu-t,n +

(47Г:

)

1/2

VE(O)-t.n -

E(OO)-t,nWТО,-t,nЕ-t,n,

-t,n =

(~;~)

1/2

VE(O)-t.n -

E(OO)-t,n

wTO,-t,nU-t,n

[Е(ОО):;n

-1]

E-t,n, (7.11)

,"",

(

)

()

LO.-t,n

E-t,n

W =

E-t,n

2 2 '

W -

wTO,-t.n

-wiЩ1,nUII.n

(47Г:

)

1/2

VE(O)II.n

E(OO)II.nWTO,II,nEII,n'

PII,n =

(~;~)

1/2

VE(O)II,n

E(OO)II,nWTO,II,nUII,n

[Е(

)~I;

EII,n' (7.12)

,"",

-w

( )

()

LТO,II,n

EII,n

W =

EII,n

2 2

W -

'""'ТО.li.n

Конечно,

модели

Лаудона

эти

шесть

уравнений

должны

быть

дополнены

следующими

тремя

материальными

уравнениями

электро

статики,

соответствующими

отсутствию

свободных

зарядов:

Е(г)

-\7ф(г),

D(r)

47ГР(г)

= E-t(w)E-t

(г)р

+ EII(w)EII(r)z,

\7·D(r)

=0,

(7.13)

Гл.

Континуальные

модели

фононое

(7.14)

где

единичные

векторы

направлении,

параллельном

оси

плоскости,

перпендикулярной

ей,

соответственно.

первом

третьем

из

этих

девяти

уравнений

было

принято, что

величины

й1..,n

UII,n

имеют

произвольную

зависимость

от

времени:

предположение

гармонической

временной

зависимости,

сделанное

приложении

А,

не

было

обязательным,

и,

просто

заменив

-u;2

на

й,

можно

непосредственно

воспроизвести

результаты

приложения

А,

не

ограничиваясь

случаем

синусоидальной

зависимости

от

времени.

Приведенная

выше

система

девяти

уравнений

представляет

собой

удобную

основу

для

описания

рассеяния носителей

на

оптических

фононах

кристаллах

решеткой

вюрцита.

Действительно,

исполь

зуя

соотношения

для

смещений,

перпендикулярных

или

параллельных

оси

С,

получаем

формулу

( )

_ 1

(

iq.r

1..(11)

fJV

LJ LJ

2mu;

еq,ЦII),j

+ a_

j=1,2,3

которая

следует

из

результатов

§ 1

гл.

Записывая

потенциал

виде

ф(Г)1..(II)

= L

ф(q)ЦII)

(7.15)

(7.16)

vE(r)1..(II) =

-\7Ф(Г)1..(II)

-iqLф(q)1..(II)

полагая

Мn,

u;2 =

u;~,

также

считая

зависимость

и(г,

сину

соидальной,

получаем

[92]

где

q1..

= qsinB,

угол

между

осью

С,

которая

принимается

качестве

оси

Кроме

того,

qll =

qcosB

e~,j,1..

e~,j,11

= 1.

Следовательно:

е(О)ЦII),n

е(

00)

1..(II),n

U;ТO,1..(II),n

(')

ф(

)

2 2

-2

q1..(II)

-u;

TO,1..(II),n

(7.18)

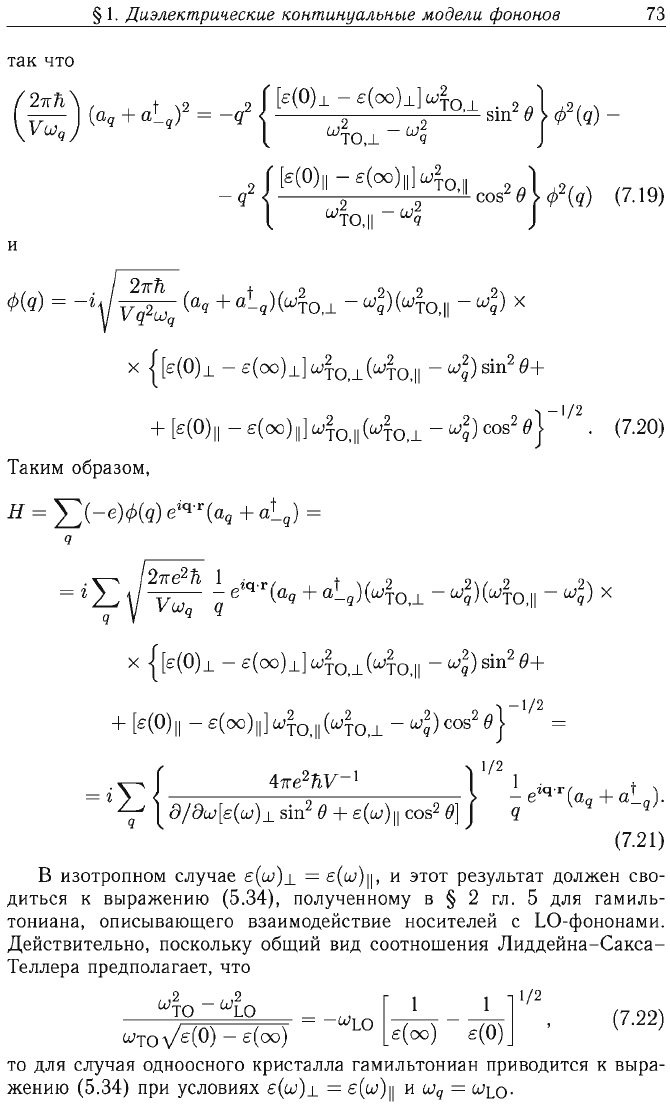
§ 1.

Диэлектрические

континуальные

модели

фононое

так

что

_.~

t 2

222

ф(q)

-2у

+a_

) (

TO,

-1

UJq)(UJTO,11

- UJ

{[Е(О)

-1

Е(

00)

-1]

UJio,-1

(UJio,11

UJ~)

sin

В+

2 2 2 2

}-1/2

[E(O)II-E(OO)II]UJ

O,II(UJ

ТO,-1

-UJq)соs

Таким

образом,

(7.20)

= 2)

-е)ф(q)

eiq.r(a

a~q)

J2~C2n

""(

t)(

2)(

- 2 6 V

UJTO.-1

- UJ

UJTO,II

- UJ

q q

(7.22)

[

1 1 ]

1/2

-UJLO

Е(ОО)

Е(О)

UJTOVE(O)

Е(ОО)

изотропном

случае

Е(

UJ)

-1

Е(

UJ)

11'

этот

результат

должен

сво

диться

выражению

(5.34),

полученному

§ 2

гл.

для

гамиль

тониана,

описывающего

взаимодействие

носителей

LО-фононами.

Действительно,

поскольку

общий

вид

соотношения

Лиддейна-Сакса

Теллера

предполагает,

что

2 2

то

для

случая

одноосного

кристалла

гамильтониан

приводится

выра

жению

(5.34)

при

условиях

E(UJ)-1

E(UJ)II

UJLO.

Гл.

Континуальные

модели

фононое

§ 2.

Модель

упругого

континуума

фононов

Как

станет

ясно

из

дальнейшего

изложения,

модель

упругого

кон

тинуума

акустических

фононов

обеспечивает

адекватное

описание

аку

стических

фононов

наноструктурах,

имеющих

размеры

примерно

до

двух

атомных

слоев.

Простым

наглядным

является

применение

этой

модели

упругого

континуума

случае

продольной

акустической

моды,

распространяющейся

квазиодномерной

структуре.

Рассмотрим

элемент

dx,

расположенный

между

точками х

+dx.

Пусть

u(х,

t) -

упругое

смещение

точке

одномерной

структуры,

т.

е.

u(х,

t) -

однородное продольное

смещение

элемента

dx.

модели

упругого

континуума

динамика

элемента

dx,

обладающего

определенной

мас

сой,

описывается

законами

Ньютона.

Действительно,

вводя

упругую

деформацию

виде

= du/dx,

упругое

напряжение

Т(х)

как

силу,

действующую

на

единицу

площади

сечения

квази-одномерной

структуры,

можем

записать

закона

Гука

следующем

виде:

Т=Уе,

(7.23)

(7.24)

где

коэффициент

пропорциональности,

называемый

модулем

Юн

га.

Динамика

элемента

dx,

имеющего

плотность

р(х),

описывается

вторым

законом

Ньютона:

(

p(x)Adx

[Т(х

+ dx) -

Т(х)]

А,

где

сечение

квази-одномерной

структуры,

рА

dx -

масса,

соответ

ствующая

элементу

dx.

соответствии

законом

Гука

(

)

(8е)

2u)

Т(х

+ dx) -

Т(х)

8х

dx =

8х

dx =

8х

dx,

(7.25)

откуда

следует

уравнение

8х

(

)

•

(7.26)

Отыскивая

решения

этого

одномерного

волнового

уравнения

виде

u(х)

~exp[i(qx

-UJt)],

где

q =

27[/>"

угловая

частота

волны,

на

ходим

дисперсионное

соотношение

для

продольной

акустической

(LA)

моды:

pUJ

= y q2

или

= vzq,

где

.jY/p.

Продольная

скорость

звука

имеет

типичные

значения

--;-

105

см/с,

так

что

при

плот

ности

= 4

г/см

модуль

Юнга

должен

иметь

порядок

1012

г-

см/с

Обобщение

этих

результатов на

трехмерный

случай

можно

полу

чить

посредством

замен

[92]

u(х)

----+

u(x,y,z)

(u,v,w)

Уе----+

----+

В,

где

Т;

CijSj.

этом

обобщении

модули

Юнга

заме

няются

матрицей

упругих

постоянных

Cij

размера

напряжение

заменяется

шестикомпонентной

величиной

;

деформация

заме

няется

шестикомпонентной

величиной

Sj.

Для

кубических

кристаллов

§2.

Модель

упругого

континуума

фононов

для

кристаллов

решеткой

цинковой

обманки

или решеткой

вюр

цита

наиболее

общий

вид

связи

между

напряжением

деформацией

Cijkl8kl,

где

k, l

принимают

значения

х,

у,

может

быть

представлен

более

простом

виде:

Т;

Cij

этом

последнем

соот

ношении

принимают

значения

от

до

причем

введены

следую

щие

обозначения:

хх

уу

2, zz

3, yz

ху

ух

Таким

образом,

имеет

вид:

дш

8з

= 8

az'

82 =

у у

ду'

(дШ

av)

84 = 8

= 8

="2

ду

(ди

дШ)

85 = 8

= 8

="2

дх

(ди

av)

86 =

у х

="2

ду

дх

Для

величины

имеют

место

следующие

соотношения:

Ть«.

у,

= T

zy,

= T

Тух.

(7.27)

(7.28)

Чтобы

упругая

энергия

определялась

однозначно,

необходимо

выпол

нение

соотношения

Cij

Cji.

Отсюда

следует,

что

матрице

име

ется

только

независимый

элемент

Cij.

Наноструктуры,

представляю

щие

широкий

интерес

современной

электронике

оптоэлектронике,

обычно

изготавливаются

из

кристаллов,

имеющих

решетку

цинковой

обманки

или

решетку

вюрцита.

Для

кубических

кристаллов,

включая

кристаллы

решеткой

цинковой

обманки,

матрица

Cij

имеет

вид

сп

С12 С12

С12

сп

С12

С12 С12

Сll

О О О О О

(7.29)

С44

О О О О

С44

О О О О

С44

Гл.

Континуальные

модели

фононое

для

кристаллов

решеткой

вюрцита:

сп

С12

С13

О О

С12

сп

С13

О О

С13

СЗЗ

О О

О О О

(7.30)

С44

(Cll

С12)/2

Для

кубической

среды,

такой

как

кристаллы

решеткой

цинковой

обманки,

из

всех

элементов

Cij

достаточно

знать

только три

незави

симые

упругие

постоянные:

Cll,

С12

С44.

изотропной

кубической

среде

выполняется

соотношение

С12

сп

2С44,

значит

только

две

постоянные,

М,

необходимы

для

определения

Cij:

С12

С13

С21

С23

С31

С32,

С44

С55

С66

(сп

С12)/2,

2м

сп

С22

СЗЗ·

(7.31)

Постоянные

называются

постоянными

Ламе.

Таким

образом,

кубическом

кристалле

модуль

Юнга

заменяется

тремя

неза

висимыми

постоянными:

Сll,

которая

связывает

напряжение

сжатия

деформацию

вдоль

одного

того

же

направления

(100),

С44,

которая

связывает

сдвиговое

напряжение

деформацию

вдоль

одного

того

же

направления,

С12,

которая

связывает

напряжение

сжатия

вдоль

одного

направления

деформацией

другом

направлении.

Для

изотропного

случая

получаются

следующие

формулы:

(7.32)

где

оператор

дu/дх

av/ay

aw/az

описывает

растяжение

сре

ды.

этом

случае

можно

непосредственно

показать,

что

трехмер

ное

обобщение

уравнения

p(x)a

2u/at

Уд

2u/д

2х

дТ/дх

дается

следующей

системой

уравнений:

§2.

Модель

упругого

континуума

фононов

2и

дТ

)

дд

'72

at2

дх

ду

+ az - /\+

/-L

дх

/-L

и,

v _

дТ

у у

aTzy _

(л

)

дд

'72

at2

дх

ду

z - +

/-L

ду

/-L

v V,

w _ aT

x z

)

дд

'72

дх

ду

+ az - /\+

/-L

az +

/-L

(7.33)

где,

как

принято,

(7.34)

литературе

часто

встречаются

две

альтернативные

формы

записи

волновых

уравнений

трехмерном

случае.

Первая

из

них

получается

путем

покомпонентной

записи

элементов

u(x,y,z)

(U\,U2,UЗ)

виде

где

СУ

1,2,3;

этом

случае

три

уравнения

могут

быть

записаны

виде

где

дТ

а{3

дт{3

(7.35)

(7.36)

этих

уравнениях

индексы

СУ

fЗ

принимают

значения

1,2,3

(соот

ветствующие

координатам

х,

у,

z),

причем

по

повторяющимся

индексам

подразумевается

суммирование,

дельта-символ

Кронекера.

Во

второй

форме

три

волновых

уравнения

записываются

просто

виде

единого

векторного уравнения:

2 2

с;

\7 u + Cz - C

gradfl,

где,

как

легко

понять,

д =

\7.

u =

divu.

(7.37)

(7.38)

Здесь

Cz -

значения

поперечной

продольной

скорости

звука:

л+2/-L

(7.39)

физической

акустике

поля

смещений

часто

описываются

посред

ством

двух

потенциальных

функций,

скалярного

потенциала

век

торного

потенциала

W =

(Чi

Чiу,

) ,

помощью

следующих

формул:

Гл.

Континуальные

модели

фононое

дф

u=-+-----

дх

ду

дф

v=-+-----

ду

дх

дф

w=-+-----

дх

ду

где

Wi (i =

х,

у,

удовлетворяют

уравнениям

(7.40)

(7.41 )

,,2,т

, =

a2Wi

v '1'% ct

i =

х,

у,

z, Ct =

Скалярный

потенциал

соответствует «безвихревой.

части

реше

ния,

векторный

потенциал

всем

остаточным

«вихревым»

полям.

литературе

безвихревые

решения

также

называют

продольными

волнами

или

волнами

сжатия

растяжения,

сейсмологи

часто

называют

эти

решения

Р-волнами.

Соответственно,

вихревые

реше

ния,

описываемые

векторным

потенциалом

Wi,

называют

поперечными,

сдвиговыми

или

сохраняющими

объем

волнами.

сейсмологии

эти

решения

обычно

называются

S-волнами.

этой

книге

безвихревые

решения,

как

правило,

будем называть

продольными

модами,

соответствующую

скорость

звука

будем

обо

значать

как

С/.

Таким

образом

вихревые

поля будем называть

попе

речными

модами,

соответствующую

скорость

звука

будем

обозна

чать

как

Ct.

Важной

проблемой,

рассматриваемой

настоящей

книге,

является

применение

продольных

поперечных

решений,

получаемых

модели

упругого

континуума,

для

описания

продольных

акустиче

ских

(LA)

поперечных

акустических

(ТА)

Фононов

нанострукту

рах.

Поэтому

принятые

здесь

обозначения

соответствуют

обозначениям

продольных

поперечных

фононов,

приняты

физике

твердого

тела.

Ежегодно

растет

количество

публикаций

об

экспериментальных

наблюдениях

акустических

мод

наноструктурах.

Примерами

таких

экспериментальных

исследований

являются

работы

[94, 5, 95].

работах

[94, 5]

сообщается

об

измерениях

характеристик

размерно

ограниченных

акустических

Фононов

очень

тонкой

металлической

фольге

проволоках

на

диэлектрических

подложках.

работе

[95]

представлены

данные

по

«сложенным»

акустическим

модам

полупроводниковых

сверхрешетках.

Принимая

во

внимание

рост

числа

таких

исследований,

§ 6

гл.

мы

распространим

рассматриваемую

настоящем

параграфе

теорию

упругого

континуума

на

случай

Называемым

также

фононами

«ломаным»

спектром.

(Примеч.

пер.)

З.

Оптические

моды

(7.42)

акустических

мод

размерно-ограниченных

структурах,

а в

гл.

рассмотрим

рассеяние

носителей

на

акустических

фононах,

как

объемных

средах,

так

размерно-ограниченных

наноструктурах.

§ 3.

Оптические

моды

размерно-ограниченных

структурах

Диэлектрическая

континуальная

модель

применялась

для

описания

свойств

размерно-ограниченных

оптических

Фононов

во

многих

элек

тронных

оптоэлектронных

при борах

на

основе

полупроводниковых

наноструктур

[10, 11,9],

представляющих

собой

квантовые

ямы,

сверх

решетки,

квантовые

проволоки

квантовые

точки.

Для

иллюстрации

фундаментальных

особенностей,

проявляющихся

при

описании

опти

ческих

фононов

помощью

диэлектрической

континуальной

модели,

рассмотрим

вначале

случай

размерного

ограничения

только

одном

направлении,

имеющий

место

квантовых

ямах

сверхрешетках.

По

сле

этого

диэлектрическая

континуальная

модель

будет

сопоставлена

другими

континуальными

моделями,

включая

гидродинамическую

модель

диэлектрическую

континуальную

модель

на

основе

комбини

рованных

мод.

Хотя

все

эти

модели

оперируют

разными

наборами

оптических

мод

размерно-ограниченных

фононов,

все

они

дают

одно

то

же

значение

частоты

рассеяния

носителей

на

фононах,

поскольку

каждая

модель

использует

полный

набор

ортогональных

фононных

мод

[96].

Вслед

за

сравнением

этих

моделей

будет

приведена

микроскопи

ческая

трактовка

размерно-ограниченных

фононных

мод.

3.1.

Диэлектрическая

континуальная

модель

мод

пластины:

нормировка

интерфейсных

мод.

Диэлектрическая

континуаль

ная

модель

предсказывает

существование

набора

размерно-ограничен

ных

оптических

фононных

мод,

которые

обычно

называются

мода

ми

пластины.

Эти

моды

могут

быть

определены

из

диэлектрической

континуальной

модели

при

наложении

электростатических

граничных

условий

на

каждой

поверхности

раздела.

Частоты

нормальных

мод

ортогональные

размерно-ограниченные

фононные моды

получают

путем

совместного

решения

уравнений,

следующих

из

диэлектрической

континуальной

модели

учетом

граничных

условий,

заключающихся

непрерывности

на

каждой

поверхности

раздела

потенциала

Ф(г)

нормальной

компоненты

вектора

D(r).

Считая,

что эти

поверхности

расположены

перпендикулярно

оси

можно

записать,

что

электроста

тический

потенциал

Фi(Г)

области

= (Zi, Zi+l)

его

двумерное

преобразование

Фурье

Фi(q,

связаны

формулой

Фi(Г)

= L

Фi(q,

э)

iq.

где р

(х, У),

q -

двумерный

волновой

вектор

плоскости

ху,

т.

е.

q = qxx.+ qyy,

где

х.

единичные

векторы.

Тогда

Гл.

Континуальные

модели

фононое

(7.43)

Ei(r)

= -

VФi(Г)

= L Ei(q, z)

iq.

Pi(r)

= xi(w)Ei(r) = L

Pi(q,

iq.

•

соответствии

§ 1

гл.

условие

нормировки мод

заключается

том,

что

энергия

фонона

моды

равна

;

для

случая

одной

поверхности

раздела,

при

z =

разделяющей

два

слоя,

т,

это

условие

имеет

вид

[

J-l

un(q,

z)]*·

[v!J-lnПn

un(q,

z)]dz+

+у

[

J-l

(

)

]

[v!J-lmПm

um,a(q,z)]

dz+

-00

+(1 -

у)

[

J-l

um,b(q,

z)]*·

[v!J-lmПm

um,b(q,

z)]dz =

2~q'

-00

(7.44)

Для

иллюстрации

процедуры

нормировки

рассмотрим

один

из

клас

сов

оптических

фононных

мод,

существующих

такой

гетероструктуре

одной

поверхностью,

разделяющей

две

различные

среды.

Волновые

уравнения

для

соответствующих

полей

допускают

этом

случае

как

гармонические,

так

экспоненциальные

решения.

Рассмотрим

реше

ния,

имеющие

экспоненциальный

характер.

Запишем

эти

моды,

назы

ваемые

интерфейсными

(IF),

следующем

виде:

Ф(г)

LФ(q,z)е-

q. р

Lce-qlzl

iq.

q q

(7.45)

откуда

Pi(q,

я)

{

;::

О,

z::::;

О,

z::::;

О,

(7.46)

где

единичный

вектор,

определяющий

направление

волнового

вектора

(qx,

qy).

Пусть

область

(z;::

О)

заполнена

веществом

представляющим

собой

бинарное

соединение,

область

::::;

О)

веществом

т,

имеющим

вид

тройного

соединения,