Строшио М., Дутта М. Фононы в наноструктурах

Подождите немного. Документ загружается.

З.

Оптические

моды

101

соответствии

электростатическими

граничными

условиями

электростатический

потенциал

Ф,

(q,

нормальная

составляющая

индукции

электрического

поля

l::iEi =

-l::iдФi(q,

z)jaz

должны

быть

непрерывны

на

каждой

границе

раздела;

таким

образом,

на

поверх

ности

Zi,

разделяющей

области

= (Zi-l,Zi)

= (Zi,Zi+l),

граничные

условия

имеют

вид

работе

[103]

использованием

обозначений

(7.104)

эти

результаты

записаны

матричной

форме:

Mi(Zi)C

м.,,

(Zi)C

(7.105)

Тогда,

начиная

вектора

Со,

относящегося

области

Ro,

вектор

столбец

С,

и,

следовательно,

электростатический

потенциал

Ф,

(q, Zi)

могут

быть

определены

любой

области

использованием

рекуррент

ных

соотношений

(7.106)

где

матрица

переноса,

связывающая

области

дается

формулой

Понятно,

что

электростатический

потенциал

для

структуры,

имеющей

поверхностей

раздела,

Ф(q,

Zi),

определяется

посредством

сшивки

решений

Фi(q,

дЛЯ

каждой

области:

Фо(q,

z), Z

Ro;

Фn(q,

z), Z

Rп.

Кроме

того,

каждой

области

значения

1::(

1::(00)

связаны

обобщенным

соотношением

Лиддейна-Сакса-

Теллера

(см.

§ 1

гл.

п.

3.3

гл.

2).

Для

интерфейсных

оптических

фононов

потенциалы

должны

экспоненциально

спадать

при

----+

±оо,

так что

для

структуры,

состоящей

из

областей,

должно

выполняться

и СО-

О.

Таким

образом,

дисперсионное

соотношение

для

этой

интерфейсной

моды

получается,

если

положить

элемент

(2,2)

матрицы

переноса

равным

нулю,

т.

е.

(7.107)

Число

мод

интерфейсных

оптических

фононов

может

быть

опре

делено

путем

исследования

дисперсионного

соотношения,

получен

ного

таким

способом;

действительно,

поскольку

каждый

вектор

102

Гл.

Континуальные

модели

фононов

пропорционален

произведению

E:i

(ш

)E:i-l

(ш)

поскольку

для

гетеро

структуры,

имеющей

границ

раздела,

столбец

Сп

является

про

изведением

матриц

столбца

СО,

то

для

бинарных

структур

дисперсионное

соотношение

имеет

зависимость

(ш

)

Таким

обра

зом,

для

подобной

гетероструктуры,

имеющей

поверхностей

раздела

состоящей

из

слоев

двухкомпонентных

(бинарных)

кристаллов,

существует

мод

интерфейсных

оптических

фононов.

Продолжая

эти

рассуждения,

приходим

заключению,

что

подобная

гетерострукту

ра

чередующимися

слоями

бинарных

трехкомпонентных

полупро

водниковых

структур

имеет

интерфейсных

оптических

фононных

мод,

поскольку

каждый

трехкомпонентный

слой

имеет

две

оптические

фононные моды

бинарного

типа.

Условие

нормировки

для

этих

мод

представляет

собой

непосред

ственное

обобщение

условия

нормировки

для

оптических

фононных

мод

простых

гетероструктурах,

именно:

(7.108)

Для

нормировки

оптических

фононных

мод

таких

структур,

имею

щих

множество

границ

раздела,

удобно

положить

()

' ( )

дФ

i (q, z)

Е,

q,Z

-\7Фi

q,z

-ЩФi

q,z

q -

()

(

)

[

. (

дФi(q,z)~]

i q, Z =

-Xi

ЩФi

q, Z q +

(7.109)

где

единичные

векторы

для

направлений

соответствен

но.

Тогда

для

области

из

предыдущего

выражения,

связывающего

упругое

смещение

электрической

поляризацией,

следует

(

)

[

• ( )

»<.

дФ

i (q,z)

-Xi

q, Z q +

Пiеi

D:ilJ,i(ei)-2(w6i

- (

)]

Отсюда

непосредственно

получаем

формулу

х1(ы)

[q'lфi(q,

z)I'

дФi~;'

1']

IМiПiUi(q,

z)1

МiПi------------

{Пiе

D:Фi(еi)-2(W6i

- (

)J}2

(7.110)

(7.111)

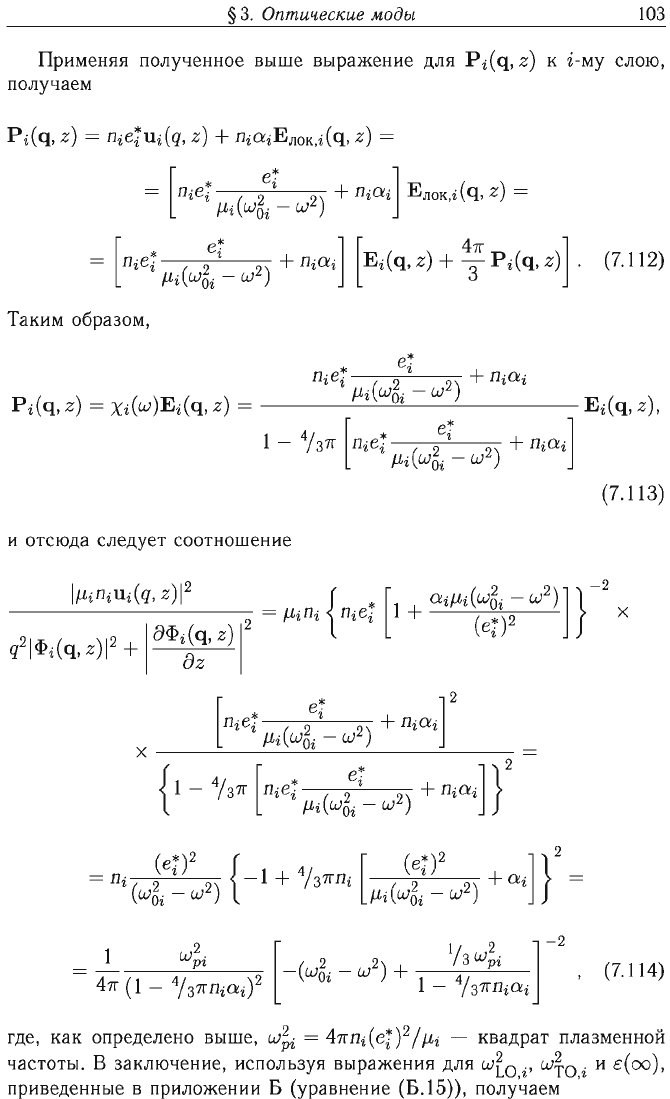
§3.

Оптические

моды

103

При

меняя полученное

выше

выражение

для

Pi(q,

i-My

слою,

получаем

Pi(q,

z) =

Пiеiщ(q,

z) +

ПiСХiЕлок,i(q,

z) =

[Пiеi

.( 2

ei_

ПiСХ

Елок,i(q,

z) =

f..t%

Таким

образом,

(7.113)

отсюда

следует

соотношение

(7.114)

где,

как

определено

выше,

W~i

47Г

л,

(еп2

f..ti

квадрат

плазменной

частоты.

заключение,

используя

выражения

для

W[O,i'

WfO,i

е(оо),

приведенные

приложении

(уравнение

(Б.15»,

получаем

104

Гл.

Континуальные

модели

фононов

1 1 &i((;))

------

41Т

2(;)

д(;)

(7.115)

&i((;)) fd

(

)12

дФi(q,

z)1

}

_п_

L.J

41Т

2(;)

ди:

z q

q, z +

2(;)L2

н,

(7.116)

Таким

образом,

для

фононного

потенциала,

записываемого

виде

Фi(q,

z) =

A(c~_e-qz

c~+e+qZ)

АФi(q,

z), (7.117)

нормировочный

коэффициент

дается

выражением

и,

следовательно,

гамильтониан

имеет

вид

еФi(Г)

e-iq'РФi(q,

z)(a~q

Le-iq'РАФi(q,z)(а~q

q).

(7.119)

Применимость

этой

формулы

можно

про

иллюстрировать,

исполь

зовав

ее

для

гетероструктур

известными

фононными

модами.

Рас

смотрим

интерфейсные

оптические

фононы

для

случая

двух

полу

бесконечных

областей

полупроводника,

граничащих

на

единствен

ной

поверхности

при

z =

О.

Понятно,

что

Фо(q,z)

= co_exp(+qz) =

= exp(+qz)

для

области

Ф1(q,z)

= C1_exp(-qz) =

exp(-qz)

для

области

О.

Тогда

1/2

[

= (

41Тп

)

&0((;))

fd 2 2

+2qz

2(;)L2

2(;)

д(;)

z q

-00

]

- 1/2

&1((;))

OOf

d 2 2 -2qz

+----

2(;)

Ви:

(41Тп)1/2{_1

[&0((;))

&1((;))]}-1/2

(7120)

2(;)L2

2(;)

д(;)

Ви:

з.

Оптические

моды

так

что

гамильтониан

принимает

вид

105

e-q1zl

(а

t +

)

у q

-q

(7.121)

идентичный

полученному

выше

результату.

Для

второго

при мера

рассмотрим

слой

одной

среды,

распо

ложенный

области

от

z =

-d/2

до

z =

+d/2

ограниченный

двумя

полубесконечными

областями

другой

среды;

например,

мы

можем

рассмотреть

квантовую

яму

толщины

из

арсен

ида

галлия,

помещенную

между

барьерами

из

арсен

ида

алюминия;

центр

квантовой

ямы

находится

при

z =

О.

этом

примере

фононный

потенциал

должен

экспоненциально

уменьшаться

для

значений

----+

±оо,

фононный

потенциал

квантовой

яме

должен

быть

комбинацией

нарастающих

затухающих

экспонент.

Рассмотрим

случай,

когда

фононный

потенциал

квантовой

яме

описывается

четной

функцией.

Пусть

диэлектрическая

проницаемость

квантовой

яме

дается

функцией

E1(U;),

диэлектрическая

проницаемость

барьеров

функцией

EO(U;).

Поскольку

принято,

что

перегородки

состоят

из

одного

материла,

то

E2(U;)

EO(U;).

Отсюда

следует,

что

функции

'lJo(q, z) =

exp[+q(z + d/2)]

для

области

z::::;;

-d/2,

'lJ

1(q,

z) =

(chqz)/(chqd/2)

для

Izl

d/2

'lJ2(q, z) =

exp[-q(z

- d/2)]

для

d/2

описывают

допустимые

формы

фононного

потенциала.

результате

имеем:

-d/2

1dz { q'l'I'o(q, z)1'+I

W~;,

1'}

-L

dz 2q'c'O'

е"

d+'IФ]

(q,

z)I'

д'l'~;,

1'}

d/2

= Jdz 2 2 ch

qz + 8h

qz = 2

d/2

-d/2 q

Jdz

2q2e-2QzеQd

= q

d/2

(7.122)

соответственно

= (

47Гn

)

1/2

[_1

дEo(u;)

дЕ1

(u;)

2 h qd ]

-1/2

гы»

2u;

Ви:

q +

2u;

au;

2 '

(7.123)

106

Гл.

Континуальные

модели

фононов

HIF=L

так

что

для

симметричного

случая

гамильтониан

имеет

вид

4пе

2hL-2

-iq·p

f ( )( t )

s q, z a_

+ a

aE:o(w)

(w)

qd q

ди;

2 (7.124)

где

fs(q,

z) = \[Ii(q, z).

Дисперсионное

соотношение

для

этой

моды

оптических

фононов

определятся

из

условия

непрерывности

нор

мальной

составляющей

индукции

электрического

поля

на

поверх

ностях

раздела.

При

z =

-dj2

это

условие

записывается

виде:

E:o(w)E

o,zlz=_dj2

= E:,(w)E"zlz=_dj2'

Отсюда

сразу

следует,

что

частоты

интерфейсных

оптических

фоно

нов

должны

удовлетворять

равенству

E:O(W)

Е:,

(w)

qdj2 =

О.

Такое

же

самое

дисперсионное

соотношение

получается

из

непрерывности

нормальной

составляющей

индукции

электрического

поля при

z = dj2.

Вспомним

теперь,

что

объемном

полупроводнике

частоты

оптических

фононов

должны

удовлетворять

условию

E:o(w)

О.

Действительно,

поскольку

выполнение

этого

условия

необходимо

для

распространения

любого

продольного

электромагнитного

возмущения,

следует

ожидать,

что

частоты

продольных

оптических

фононов

должны

удовлетворять

этому

дисперсионному соотношению.

случае

структуры,

состоящей

из

двух

материалов,

двумя

поверхностями

раздела

частоты

интерфейсного

продольного

оптического

фонона

зависят

как

от

Е:о

(w),

так

от

Е:,

(w).

Выражение

для

гамильтониана

HIF

идентично

выражению,

полученному

работе

[91],

может

быть

переписано

виде,

приведенном

работе

[90].

Мода,

описываемая

этим

гамильтонианом,

является

симметричным

интерфейсным

оптическим

фононом

для

рассматриваемой

квантовой

ямы.

Рассмотрим

(последний)

пример:

если

\[Io(q, z) = - exp[+q(z + dj2)]

для

области

:::;;

-dj2,

\[1, (q,z) = (shqz)j(shqdj2)

для

Izl

< dj2

\[I2(q, z) = exp[-q(z - dj2)]

для

;::

dj2,

то

для

антисимметричного

случая

гамильтониан

имеет

вид:

HIF=L

4пе

2hL-2

&o(w) +

(w)

cth

ди; ди;

где

(q,z) =

\[1

i (q,z).

Как

выше,

дисперсионное

соотношение

для

этой

моды

получается

из

требования

непрерывности

на

поверхности

раздела

нормальной

составляющей

индукции

электрического

поля.

этом

случае

выполняется

равенство

E:O(W)

Е:,

(w)

cth

qdj2 =

О.

Этот

результат

воспроизводит

гамильтониан,

выведенный

§3.

Оптические

моды

107

работе

[91]

для

антисимметричного

интерфейсного

оптического

фонона

рассматриваемой

системе,

содержащей

квантовую

яму.

Подход,

основанный

на

матрицах

переноса,

предложенный

рабо

те

[103],

может

быть

использован

для

лучшего

понимания

природы

фононов

сверхрешетках.

Действительно,

применение

метода

матриц

переноса

структуре

AIAs/GaAs

множественными

барьерами,

изоб

раженной

на

рис.

7.6,

а,

при

водит

дисперсионным

соотношениям

наподобие

тех,

которые

графически

изображены

на

рис.

7.7

для

раз

личных

гетероструктур

AIAs/GaAs.

11--

Рис.

7.6.

Профили

распределения

потенциала

для

гетероструктуры

AIAs/GaAs

множеством

барьеров

(а)

для

асимметричной

гетероструктуры

пятью

поверхностями

раздела

(6).

Из

работы

[103],

печатается

разрешения

Амери-

канского

института

физики

гл.

будет

показано,

что

гетероструктура

пятью

поверх

ностями

раздела,

изображенная

на

рисунке

7.6,

б,

представляет

ин

терес

для

полупроводниковых

лазеров

узкими

ямами.

Метод

мат

риц

переноса,

предложенный

работе

[103],

может

применяться

при

определении

дисперсионных

соотношений

для

интерфейсных

фононов

соответствующих

этим

фононам

потенциалов.

Для

случая,

когда

два

барьера,

приведенные

на

рис.

7.6,

б,

изготовлены

из

Alo.6Gao.4As,

низкий

барьер

на

левом

краю

из

Alo.2SGaO.7SAs,

дисперсионные

соотношения

имеют

такой

же

вид,

как

на

рис.

7.8,

пять

интер

фейсных

мод

типа

мод

AIAs -

вид,

представленный

на

рис.

7.9.

Как

было

показано

выше,

такой

гетероструктуре

пятью

поверхностями

раздела,

состоящей

из

слоев

бинарного

полупроводника

тройного

сплава,

существуют

интерфейсных

мод.

Действительно,

как

было

показано

ранее,

такие

структуры,

имеющие

поверхностей

раздела

чередующимися

слоями

бинарных

трехкомпонентных

полупроводни

ков,

имеют

интерфейсных

оптических

фононных

мод.

Подход,

основанный

на

матрицах

переноса

(см.

[103]),

также

поле

зен

для

понимания

свойств

интерфейсных

фононов

гетероструктурах

двумя

барьерами,

подробно

исследуемых

связи

новыми

типами

электронных

диодов

транзисторов.

Как

будет

показано

гл.

10,

так

называемый

долинный

ток

таких

структурах

двумя

барьерами

108

Гл.

Континуальные

модели

фононов

Частота

фонона

(мэВ)

5.0

4.5

4.0

3.5

l.L.L>.-l..LuL1..LL.o..1..L>.J.l..uLL1..u l.L.L>.-l..LuL1..LL.o..1..L>.J.l..uLL1..u

l.LLL.l..LuL1..LLLi..L.LJ.l..u-L1..u

l.LLL.l..Lu-l..L.LL1..LL.L1..L>-L1..u

Волновой

вектор

(qa)

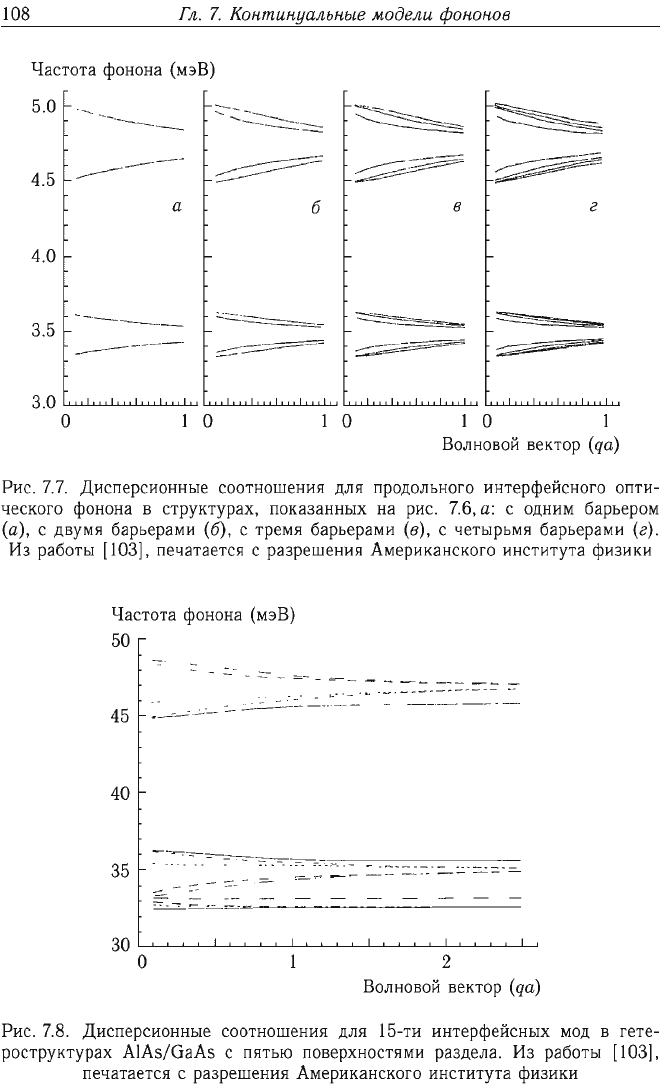
Рис.

7.7.

Дисперсионные

соотношения

для

продольного

интерфейсного

опти

ческого

фонона

структурах,

показанных

на

рис.

7.6,

а:

одним

барьером

(а),

двумя

барьерами

(6),

тремя

барьерами

(в),

четырьмя

барьерами

(г).

Из

работы

[103],

печатается

разрешения

Американского

института

физики

Частота

фонона

(мэВ)

- -

=---

----

~--

45 ------

:......--_._---

---

=_.,.-.

=--Т-

---

Волновой

вектор

(qa)

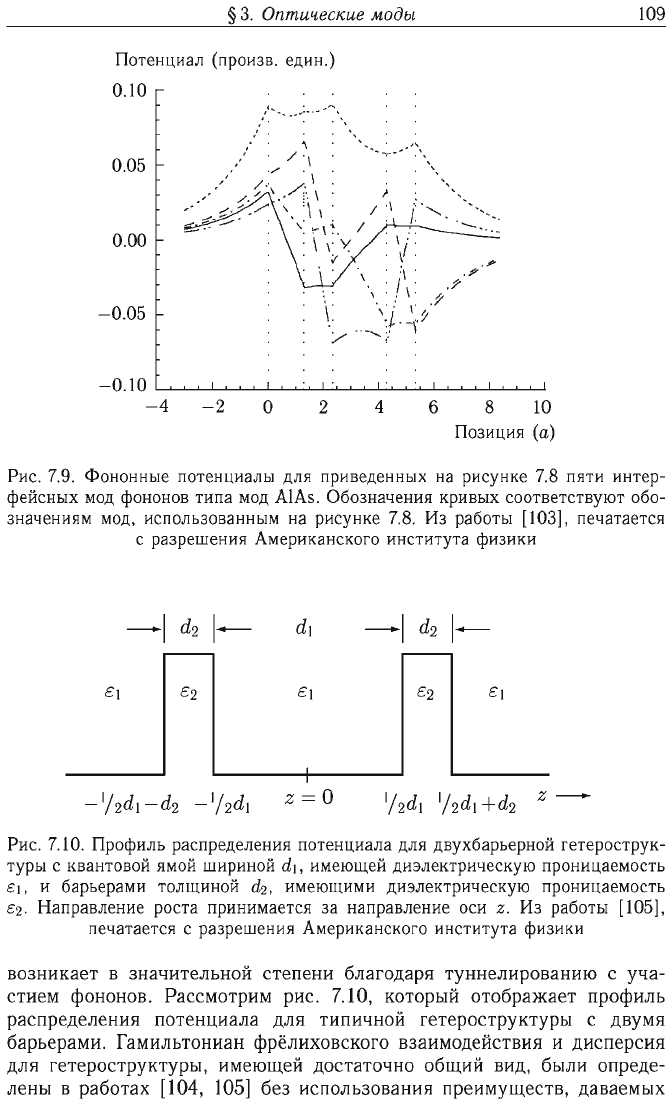
Рис.

7.8.

Дисперсионные

соотношения

для

15-ти

интерфейсных

мод

гете

роструктурах

A1As/GaAs

пятью

поверхностями

раздела.

Из

работы

[103],

печатается

разрешения

Американского

института

физики

§3.

Оптические

моды

109

Потенциал

(произв.

един.)

0.10

/<""

.~~:~

.......

.' .

0.05

0.00

-0.05

8 10

Позиция

(а)

-2

-0.1

'---'-~...J......L~--'-~-'-'-~--L.....J~~"""""~--'----'~'-'

-4

Рис.

7.9.

Фононные

потенциалы

для

приведенных

на

рисунке

7.8

пяти

интер

фейсных

мод

фононов

типа

мод

AIAs.

Обозначения

кривых

соответствуют

обо

значениям

мод,

использованным

на

рисунке

7.8.

Из

работы

[103],

печатается

разрешения

Американского

института

физики

z=o

Рис.

7.10.

Профиль

распределения

потенциала

для

двухбарьерной

гетерострук

туры

квантовой

ямой

шириной

d\,

имеющей

диэлектрическую

проницаемость

$\,

барьерами

толщиной

d2,

имеющими

диэлектрическую

проницаемость

$2.

Направление

роста

принимается

за

направление

оси

Из

работы

[105],

печатается

разрешения

Американского

института

физики

возникает

значительной

степени

благодаря

туннелированию

уча

стием

фононов.

Рассмотрим

рис.

7.10,

который

отображает

профиль

распределения

потенциала

для

типичной

гетероструктуры

двумя

барьерами.

Гамильтониан

фрёлиховского

взаимодействия

дисперсия

для

гетероструктуры,

имеющей

достаточно

общий

вид,

были

опреде

лены

работах

[104, 105]

без

использования

преимуществ,

даваемых

110

Гл.

Континуальные

модели

фононов

методом

матриц

переноса

[103].

Эти

результаты

можно

обобщить

следующим

образом.

Гамильгониан

фрёлиховского

взаимодействия

для

симметричных

интерфейсных

мод

продольных

оптических

фононов

имеет

вид

= L

4ne2JiL

-2

[&,

(u;)

(th

qd, +

а2)

+ &2(u;)

(ь2

с2)(1

2qd2)]

-'/2

ОU;

1·

(а

)

-q

(chqz)/(chqd,/2)

d,/2

+ d

:'( z,

d,/2

:'( z :'(

d,/2

+ d

Izl

:'(

d,/2,

-d,/2

- d

:'( Z

:'(

-d,/2,

z:'(

-d,/2

- d2,

(7.126)

гамильгониан

фрёлиховского

взаимодействия

для

антисимметричных

мод

имеет

вид

HIF,A

Lqv4пе2JiL-2

(shqz)/(shqd,/2)

d,/2

+ d

:'( z,

d,/2

:'( z :'(

d,/2

+ d2,

Izl

:'(

d,/2,

-d,/2

- d

:'( Z

:'(

-d,/2,

z:'(

-d,/2

- d

(7.127)