Строшио М., Дутта М. Фононы в наноструктурах

Подождите немного. Документ загружается.

Приложенив

281

отсутствие

свободных

зарядов

(\7 . D =

О)

дисперсионные

соот

ношения

двух

областях,

соответствующих

разным

веществам,

имеют

вид:

E(UJ)II,lq~,1

E(UJ)1..,lq2

О,

E(UJ)II,2q~,2

E(UJ)1..,

О,

E(UJ)II,IE(UJ)l..,1

О,

E(UJ)II,2E(UJ)1..,2

О,

при

Izl

< dj2,

при

Izl

> dj2.

(Г.39)

Очевидно,

что

непрерывность

тангенциальной

составляющей

элек

трического

поля

на

границах

раздела

уже

обеспечена

выбором

вида

функции

ф(r).

Непрерывность

нормальной

составляющей

индукции

электрического

поля

на

поверхностях

раздела

при

водит

следующему

требованию:

E(UJ)II,lqll

sinqll,ldj2 -

Е(UJ)II,2К;2

cosqll,2dj2 =

О.

Как

выше,

условие

нормировки

из

п.

3.1

гл.

(Г.40)

= J

(_1

дE'(UJ)l..,n

IEl..nl

+ _1

дE'(UJ)II,n

2UJ

47Г

2UJ

aUJ

47Г

2UJ

aUJ

11,

(Г.41

)

можно

упростить,

используя

интегралы

от

входящих

него

величин

IEl..,n12

2IФ(z)1

IEII,nI

lдФ(z)jдzI

Для

симметричного

случая

эти

интегралы

имеют

вид

СХ)

L J

дE'~21..,n

El..,n1

n=I_CX)

2ф

[дE'(UJ)l..,1

+ 1 , qll,ld Qll,ld)] +

- Q

-'-::--'-----'---

-sш--соs--

aUJ

Qll,l

2 2

2ф2

( 1

дE'(UJ)1..,2

2Qll,ld)

СОБ

К;2

aUJ

(Г.42)

СХ)

" J

дE'(UJ)II,n

г:

aUJ

EII,n-

n=l

-СХ)

(Г.43)

_--=--"-'---

1_sin

Qll,ld

СОБ

Qll,ld)] +

Qll,l

2 2

(дE'(UJ)II,2

2Qll,ld)

Фа

aUJ

К;2

СОБ

-2-

[дE'(UJ)II,1

Фа

aUJ

условие

нормировки

при

обретает

вид

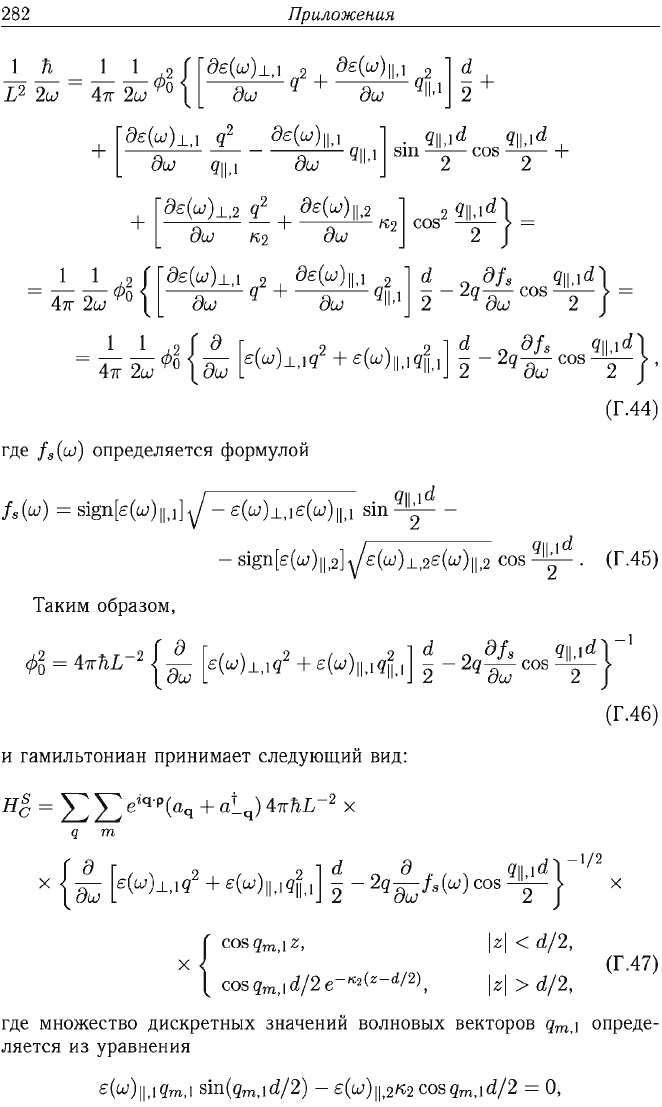
282

Приложения

где

(UJ)

определяется

формулой

18(UJ)

sign[E(UJ)II,IJV

E(UJ)-t,IЕ(UJ)

11,1

sin

sigП[Е(UJ)II,2JVЕ(UJ)-t,2Е(UJ)II,2

cos

q1l2

(Г.45)

Таким

образом,

-2{

8 [ 2

818

Qll,ld}-l

Фа

= 4JrnL

8UJ

E(UJ)-t,IQ

E(UJ)II,IQII,1

8UJ

cos

-2-

(Г.46)

гамильтониан

принимает

вид:

LLeiQ'P(aq

+а~Q)4JrnL-2

{

COSQm,IZ,

COS

Qm,l

d/2

e-I'C2(z-d/2)

Izl

d/2,

Izl

d/2,

(Г.4

где

множество

дискретных

значений

волновых

векторов

Qm,l

опреде

ляется

из

уравнения

Приложенив

283

fs(VJ)

определяется

для

дискретных

значений

qll,l,

qm,l,

удовлетво

ряющих

неравенству

2mn/d

qm,l

< 2(m +

l)n/d.

(Г.48)

Как

показано

выше,

""2

= V

E(VJ)1..,2/

E(VJ)

11,2

Путем

аналогичных

рас

суждений

можно

получить

случае

антисимметричных

мод

следующее

выражение

для

гамильтониана:

LLeiQ'P(aq

+а~Q)4n1iL-2

{

[ 2 2 ] d

qll

1d }

-1

aVJ

E(VJ)l..,lq

E(VJ)II,lqll,1

- 2q

aVJfa(VJ)

sш

где

Izl

< d/2,

Izl

> d/2,

(Г.49)

fs(VJ)

= sign[E(VJ)II,IJV -

E(VJ)l..,1E(VJ)II,1

cos

sign[E(VJ)

11,2]

(

)

1..

(

)

11,2

sin

qll2

(Г.50)

где

дискретные

значения

волновых

векторов

qm,l

определяются

из

уравнения

(Г.51

)

при

выполнении

условий

2(m -

l)n/d

qm,l

< 2(m +

l)n/d

""2 =

VE(VJ)1..,2/

E(VJ)

11,2

~oды

полупространства

структуре

двумя

поверхностями

раз

дела

наиболее

просто

можно

проанализировать

использованием

сим

метричных

антисимметричных

мод,

поскольку

такая

гетероструктура

является

симметричной

относительно

плоскости

z =

О.

Запишем

сим

метричные

моды

виде

. {

Acos[qll,1

(z + d/2)] -

sin[qll,1

(z + d/2)],

ф(r)

""IZ,

Acos[qll,l(z - d/2)] + Bsin[QII,I(z - d/2)],

z <

-d/2,

Izl

< d/2,

z > d/2.

(Г.52)

284

Приложения

Тогда

непрерывность

тангенциальной

составляющей

электрического

поля

на

поверхностях

раздела

дает

условие

сh(к;,d/2),

непрерывность

нормальной

составляющей

индукции

элек

трического

поля

на

поверхностях

раздела

требует

выполнения

равенства

e(u;)11,2qll,2B

е(U;)II,'К;2С

sh(к;,d/2).

Поскольку

\7.

D =

О,

то

имеет

место

соотношение

e(u;)11,2q~,2

e(u;)..l,

О.

Вводя

обозна

чение

.6.3

е(U;)11,2qll,2/е(U;)II,'К;',

получаем,

что

В.6.

сth(к;,d/2).

Тогда,

положив

Фа,

получаем

sin[qll,1

(z + d/2)] +

+.6.3

cth

к;,d/2

cos[qll,' (z + d/2)],

Ф(r)

Фаеiq.р

.6.

(

к;

)

(

к;

)

sin[qll,' (z - d/2)] +

+.6.3

cth

к;,d/2

cos[qll,' (z - d/2)],

что

можно

записать

виде

{

sin[qll,,(lzl-

d/2)] +

ф(r)

Фа

.6.3

cth

к;,d/2

cos[qll,' (Izl - d/2)

.6.3

(ch

к;,

z)/

(sh

к;,

d/2),

Антисимметричные

моды

запишем

виде

z <

-d/2,

Izl < d/2,

d/2,

(Г.53)

Izl > d/2,

Izl < d/2.

(Г.54)

-АсоS[QII,'

(z + d/2)] +

sin[QII,'

(z + d/2)],

ф(r)

= e

Сshк;,z,

Acos[QII,'(z - d/2)] +

sin[QII,'

(z - d/2)],

z <

-d/2,

Izl < d/2,

d/2.

(Г.55)

Тогда

непрерывность

тангенциальной

составляющей

электрического

поля

на

поверхностях

раздела

дает

условие

Сsh(к;,d/2),

непре

рывность

нормальной

составляющей

индукции

электрического

поля

на

поверхностях

раздела

требует

выполнения

равенства

e(u;)11,2QII,2B

е(U;)II"к;,Ссh(к;,d/2).

Таким

образом,

отсюда

следует,

что

В.6.

th(к;,d/2).

Тогда

при

Фа

получаем

Приложенив

285

sin[qll,1

(z + d/2)] -

thh:\d/2

cos[qll,\

(z+d/2)], z <

-d/2,

Ф(Г)

Фо

~з(sh

h:\z)/(chh:\d/2), Izl < d/2,

sin[qll,\(z - d/2)] +

h:\

d/2

cos[qll,1

(z - d/2)], z > d/2,

(Г.56)

или,

другом

виде:

{

sign(z){

sin[QII,2(lzl

- d/2)] +

ф(г)

Фо

thh:\d/2cos[QII,2(lzl- d/2)]},

(sh

h:\

z)/ (ch

h:\

d/2),

Как

выше,

условие

нормировки

из

п.

3.1

гл.

Izl > d/2,

Izl < d/2.

(Г.57)

= J

(_1

дE(w)..l,n

IE..lnl

дE(w)ll,n

)

L2 2w

47Г

2w aw '

47Г

Всо

11,

(Г.58)

может

быть

переписано

использованием

соответствующих

интегралов

от

величин

IE..l,nI2

2IФ(z)1

IEII,nI

lдФ(z)/дzI

Для

симметрич

ного

случая

пределе

L ----t

вклад

вносят

следующие

интегралы:

L/2

(

2 2

..l,21

dz =

фоQ

cth h:\d/2

"2'

d/2

Ц2

(

2 2

EII,21

dz =

ФоQII,2

cth h:\d/2

"2'

d/2

для

антисимметричного

случая

интегралы

(Г.59)

(Г.60)

286

Приложения

и,

таким

образом,

получаем

{ (1

+~§сthfчd/2)-'

(1 +

~§thfчd/2)-'

симметричный

случай,

антисимметричный

случай.

(Г.61)

Тогда

гамильтониан

взаимодействия

для

симметричных

мод

полу

пространства

записывается

виде

Izl < d/2,

Izl >

.иг,

(Г.62)

eiq,p(aq +

a~q)

2 (q2 +

q~,2)

E~"

I\;T

l\;,d/2+

E~,2q~,2

l\;,d/2

{

EII"I\;,

shl\;,d/2sin[qll,2(l

zl-

d/2)] +

EII,2qll,2

1\;,

d/2

cos[qll,2(lzl

- d/2)],

EII,2qll,2

I\;,z,

где

суммирование

ведется

по

qll,2

(Г.62)

берутся

только

те

ве

личины,

для

которых

E(W)II"E(W)-l,1

О.

Подобным

же

образом

га

мильтониан

взаимодействия

для

симметричных

мод

полупространства

записывается

следующем

виде:

(Г.63)

Izl < d/2.

Izl > d/2,

eiq,p(aq +

a~q)

2 (q2 +

q~,2)

E~"

I\;Tch

l\;,d/2+

E~,2q~,2

l\;,d/2

{

sign(Z){EII,1I\;' chl\;,d/2sin[qll,2(lzl-

d/2)] +

EII,2QII,2

shl\;,d/2

cos[QII,2(lzl

- d/2)J},

EII,2QII,2

I\;,z,

Приложенив

287

Гамильтониан

взаимодействия

для

распространяющихся

мод

можно

по

лучить

напрямую

из

гамильтонианов

для

мод

полупространства

путем

подстановки

h:l

----t iqll,l.

Действительно,

эта

замена

приводит

соотно

шению

.6.3

-i.6.~,

где

(Г.64)

Izl > dj2,

Izl < dj2,

(Г,65)

Izl > dj2,

Izl < dj2.

(Г.66)

Тогда

гамильтониан

взаимодействия

для

распространяющихся

симмет

ричных

мод

записывается

виде

eiq,p(a

q +

a~q)

(E(UJ)II,lq~,1

sin

qll,ldj2 +

E(UJ)II,2q~,2

СОБ

qll,ldj2)

{

sign(z){

EII,2qll,2

cosqll,ldj2 cos[qll,2(lzl- dj2)] -

EII,lqll,l

sinQII,ldj2sin[qll,2(lzl-

dj2)]},

EII,2QII,2

СОБ

QII,IZ,

где

суммирование

ведется

по

QII,2

берутся

только

те

величины,

для

которых

E(UJ)II,IE(UJ)l..,1

О.

Аналогичным

образом

гамильтониан

взаи

модействия

для

распространяющихся

антисимметричных

мод

записы

вается

следующем

виде:

eiq.p(a

a~q)

(E(UJ)II,IQ~,1

СОБ

QII,ldj2 +

E"(UJ)II,2Q~,2

sin

QII,ldj2)

{

sign(z){

E"11,2QII,2

sinQII,ldj2cos[QII,2(lzl- dj2)] +

EII,I.QII,l

cosQII,ldj2sin[QII,2(lzl-

dj2)]},

E"11,2QII,2

sш

Qll,lz,

288

Приложения

Приложение

Д:

золотое

правило

Ферми

Золотое

правило

Ферми

обеспечивает

удобный

способ

расчета

частот

рассеяния

носителей

на

фононах,

основанный

на

теории

возмущений.

При

расчете

этих

частот

твердых

веществах

обычно

допустимо

рассматривать

взаимодействие

носителей

фононами

как

возмущение

гамильтониана,

описывающего

систему

отсутствие

фононного

взаимодействия.

Обозначая

гамильтониан

невозмущенной

системы

через

Н,

гамильтониан

взаимодействия

носителей

фононами

через

Hc-p(t),

получаем

уравнение

для

волновой

функции

системы

'Ф(х,

t):

a'IjJ(x,

[Н

Hc_p(t)]'IjJ(x,

t) =

----;-

z t

(Д.!)

где

для

простоты

рассматривается

одномерная

система.

окончатель

ном

виде

золотое

правило

Ферми

не

будет

зависеть

от

допущения

одномерности.

Взяв

волновую

функцию

виде

(Д.2)

где

фn(х)

является

собственным

состоянием

невоэмущенной

системы

квантовым

числом

п,

получаем

два

равенства:

a'IjJ(x,

t) =

" dcn(t)

(х)

e-iЕnt/1i

i at

dt n

+ L

сn(t)Еnфn(х)

e-iЕnt/1i.

(ДА)

Отсюда

без

использования

каких-либо

приближений

получаем

dc~?)

фn(х)

e-iЕnt/1i

= Lcn(t)

e-iЕnt/1i

Нс-р(t)фn(х).

n n

(Д.5)

Поскольку

набор

собственных

состояний

Фn

квантово-механической

системы

является

полным,

то

(Фтlфn)

учетом

этого,

умножая

Приложение

289

обе

части

последнего

уравнения

на

ф~

интегрируя

по

х,

получаем

множество

уравнений

.н

dC;t(t) =

2:)ФmI

Нс-р(t)

Фn)

i(Е

n-Е

rn)t/1i

cn(t).

(Д.б)

Теперь,

если

допустить,

что

система

изначально

находится

состоя

нии

п,

так что

сn(О)

= 1,

все

другие

коэффициенты

сm(О)

равны

нулю,

то

временная

эволюция

состояния

может

быть

приближенно

описана

выражением

cm(t)

fdt

(ФmIНс-р(t)1

Фn)

(

)

(Д.?)

случае,

когда

Hc-p(t)

имеет

вид

ступеньки,

(

)

- 1

cm(t) =

(ФmIНс-рl

Фn)

(Д.8)

(

I(Ф

)12

sin

[(E

- E

m)t/(2n)]

с-р

[(Е

m)/2]2

(Д.9)

(Д.11

)

случае,

когда

состояния

близки

вырождению,

"'"

когда

переход

из

состояния

происходит

одно

из

множества

конечных

состояний,

плотно

сосредоточенных

вокруг

выражение

для

веро

ятности

перехода

m(t)1

принимает

вид

n+t::..E/2

= f dE

(Е)I(Ф

)12

sin

[(E

- E

m)t/(2n)]

с-р

[(Е

)

]

n-t::..Е/2

n+t::..E/2

= 4

(Е)I(Ф

)12

f dE sin

[(E

- E

m)t/(2n)]

с-р

[(Е

m)/2]2

n-t::..Е/2

(Д.10)

где

последний

результат

получен

учетом

того,

что

произведе

ние

р(Е)I(ФmIНс_РIФn)12

слабо

зависит

от

энергии

по

сравнению

множителем

[sin

E)t/(2h)]/(E

Е)2.

Вводя

обозначение

(Е

- E)t/(2h),

перепишем

полученную

формулу

виде

tt::..E/41i

2t 2 f sin

= h

р(Е)I(ФmIНс-рl

Фn)1

-tt::..Е/41i

М.

А.

Сторшио,

М.

Дутта

290

При

больших

значениях

Приложения

скорость

перехода

дается

выражением

2n 2

= h

р(Е)I(ФmIНс-рl

Фn)1

(Д.12)

(Д.13)

Эта

формула

описывает

одно

из

выражений

для

так

называемого

золо

того

правила

Ферми.

Альтернативную

форму

представления

золотого

правила

Ферми

можно

получить,

вернувшись

случаю

перехода

между

двумя

состоя

ниями

т)

пределе

больших

значений

t»--=---

'-'J

Используя

соотношение

sin

'-'Jmnt

( /2)2 ----7

27Г15('-'J

nt)

= -

rS(n'-'J

mn)

'-'Jmnt

для

t »

2/'-'J

mn,

получаем

(Д.14)

(Д.15)

(Д.16)

случае,

когда

гамильтониан

связан

полем

фонона

и,

таким

образом,

имеет

гармоническую

временную

зависимость

ехр(±i'-'Jфонt)

последнем

выражении

необходимо

заменить

'-'J

на

'-'J

'-'Jфон,

причем

верхний

знак

соответствует

эмиссии

фононов,

нижний

связан

поглощением

фононов;

таким

образом,

получаем

Именно

данная

формулировка

золотого

правила

Ферми

широко

используется

этой

книге.

Вывод

золотого

правила

Ферми

основыва

ется

на

предположении,

что

t »2/'-'J

mn.

то

же

время

для

многих

приборов,

работающих

нано-масштабе,

это

условие

не

соблюдается.

Действительно,

для

нан опри

боров

времена

перехода

часто

составляют

0,1

пс

менее,

разница

энергий

от

нескольких

единиц

до десятков мэВ,

что

соответствует

2/'-'J

':2'

О,

пс.

Следовательно,

выполняется

соотношение

2/'-'J

mn,

анеравенство

t»

2/'-'J

не

удовлетворяется.

Тем

не

менее

золотое

правило

Ферми

регулярно