Строшио М., Дутта М. Фононы в наноструктурах
Подождите немного. Документ загружается.

§4.
Увеличение
инверсии
населенности
Распределение
энергии
электронов
(мэв-
1
)
0.05
а
241
0.04
0.03
0.02
0.01
О
ООО~l
...
I
••••
I
••
~
••
б,
О
100 200 300 400
Энергия
электрона
(мэВ)
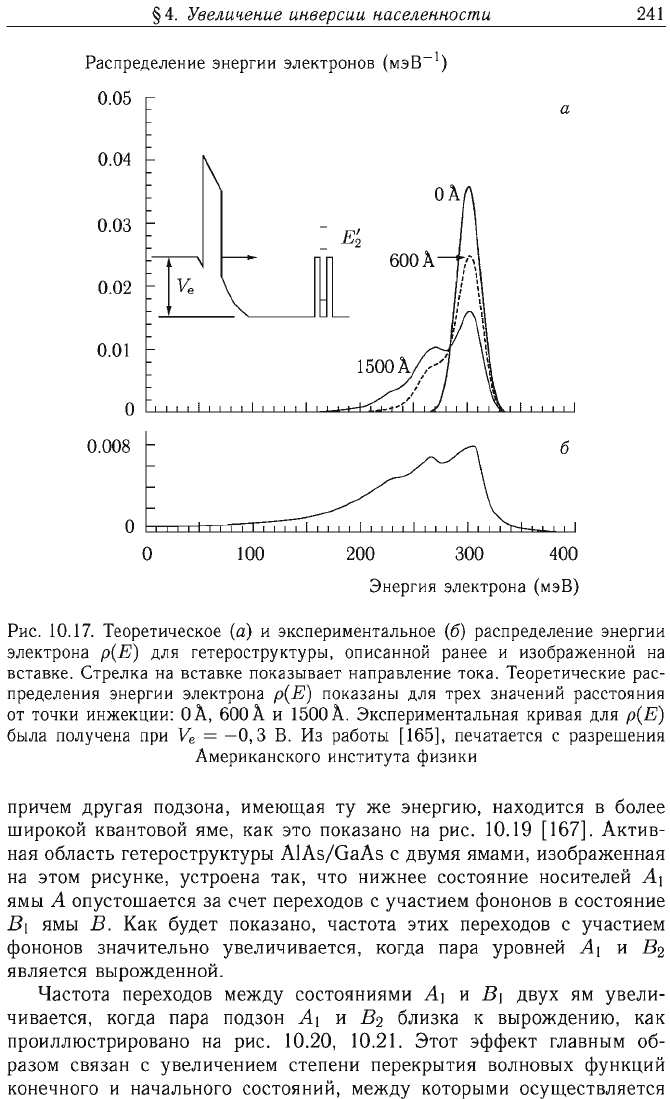
Рис.
10.17.
Теоретическое
(а)
и
экспериментальное
(6)
распределение
энергии
электрона
р(Е)
для
гетероструктуры,
описанной
ранее
и
изображенной
на
вставке.
Стрелка
на
вставке
показывает
направление
тока.
Теоретические
рас
пределения
энергии
электрона
р(Е)
показаны
для
трех
значений
расстояния
от
точки
инжекции:
О
'А,
600'А
и
1500
'А.
Экспериментальная
кривая
для
р(Е)
была
получена
при
V
e
=
-0,3
В.
Из
работы
[165],
печатается
с
разрешения
Американского
института
физики
причем
другая
подзона,
имеющая
ту
же
энергию,
находится
в
более
широкой
квантовой
яме,
как
это
показано
на
рис.
10.19 [167].
Актив
ная
область
гетероструктуры
AIAs/GaAs
с
двумя
ямами,
изображенная
на
этом
рисунке,
устроена
так,
что
нижнее
состояние
носителей
А,
ямы
А
опустошается
за
счет
переходов
с
участием
фононов
в
состояние
В,
ямы
В.
Как
будет
показано,
частота
этих
переходов
с
участием
фононов
значительно
увеличивается,
когда
пара
уровней
А,
и
В
2
является
вырожденной.
Частота
переходов
между
состояниями
А,
и
В,
двух
ям
увели
чивается,
когда
пара
подзон
А,
и
В
2
близка
к
вырождению,
как
проиллюстрировано
на
рис.
10.20, 10.21.
Этот
эффект
главным
об
разом
связан
с
увеличением
степени
перекрытия
волновых
функций
конечного
и
начального
состояний,
между
которыми
осуществляется
242
Гл.
10.
Последние
разработки
Коэффициент
передачи
фототока
0.15
0.1
0.05
О
•
• •
• t
•
.А
.JlC
.1lC
-IJ.(
-1iX
:1jtC
_
Jl'o
О
-1
-2
-3
-4
-5
Напряжение
эмиттера
(В)
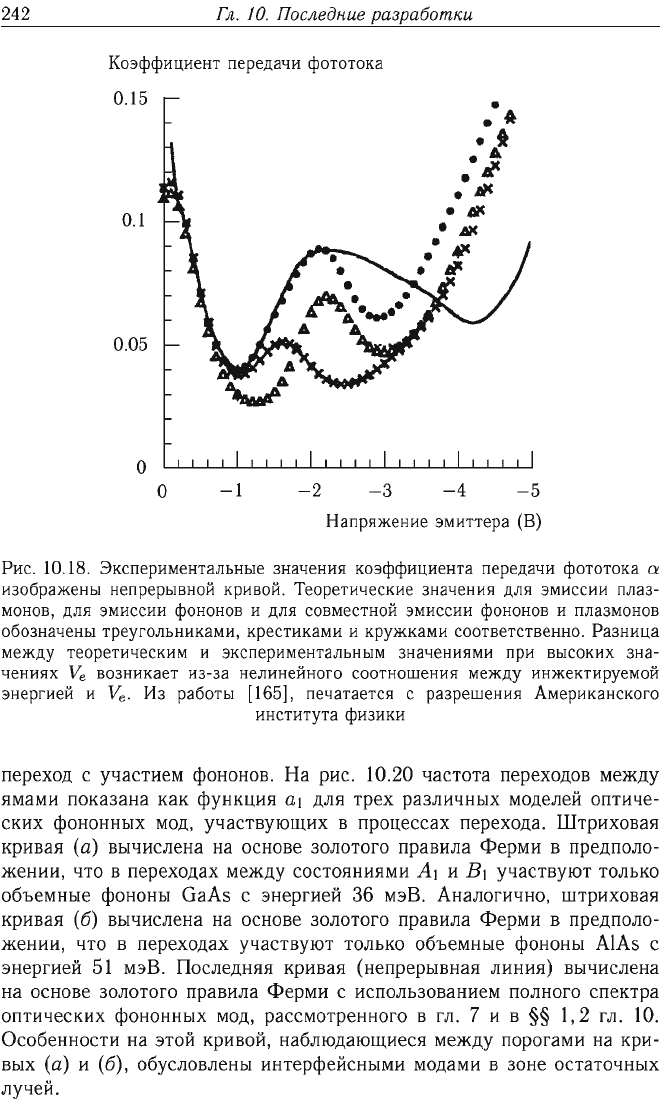
Рис.
10.18.
Экспериментальные
значения
коэффициента
передачи
фототока
СУ
изображены
непрерывной
кривой.
Теоретические
значения
для
эмиссии
плаз
монов,
для
эмиссии
фононов
И
для
совместной
эмиссии
фононов
и
плазмонов
обозначены
треугольниками,
крестиками
и
кружками
соответственно.
Разница
между
теоретическим
и
экспериментальным
значениями
при
высоких
зна
чениях
V
e
возникает
из-за
нелинейного
соотношения
между
инжектируемой
энергией
и
V
e
.
Из
работы
[165],
печатается
с
разрешения
Американского
института
физики
переход
с
участием
фононов,
На
рис.
10.20
частота
переходов
между
ямами
показана
как
функция
а,
для
трех
различных
моделей
оптиче
ских
фононных
мод,
участвующих
в
процессах
перехода.
Штриховая
кривая
(а)
вычислена
на
основе
золотого
правила
Ферми
в
предполо
жении,
что
в
переходах
между
состояниями
А,
и
В,
участвуют
только
объемные
фононы
GaAs
с
энергией
36
мэБ.
Аналогично,
штриховая
кривая
(6)
вычислена
на
основе
золотого
правила
Ферми
в
предполо
жении,
что
в
переходах
участвуют
только
объемные
фононы
AIAs
с
энергией
51
мэБ.
Последняя
кривая
(непрерывная
линия)
вычислена
на
основе
золотого
правила
Ферми
с
использованием
полного
спектра
оптических
фононных
мод,
рассмотренного
в
гл.
7
и
в
§§
1,2
гл.
10.
Особенности
на
этой
кривой,
наблюдающиеся
между
порогами
на
кри
вых
(а)
и
(6),
обусловлены
интерфейсными
модами
в
зоне
остаточных
лучей.
а
§4.
Увеличение
инверсии
населенности
243
б
711
300
200
7
0 u
t
Е
з
100
О
3
4
5
6 7
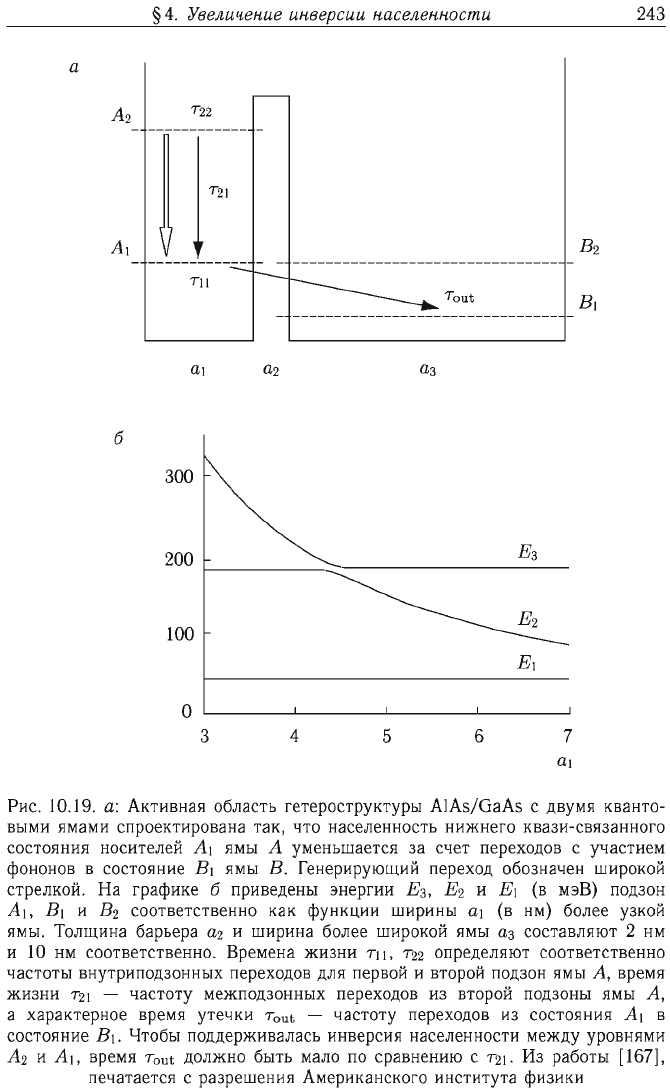
Рис.
10.19.
а:
Активная
область
гетероструктуры
AIAs/GaAs
с
двумя
кванто
выми
ямами
спроектирована
так,
что
населенность
нижнего
квази-связанного
состояния носителей
Аl
ямы
А
уменьшается
за
счет
переходов
с
участием
фононов
в
состояние
В\
ямы
В.
Генерирующий
переход
обозначен
широкой
стрелкой.
На
графике
б
приведены
энергии
Е
з,
Е
2
и
Е,
(в
мэВ)
подзон
А
1
,
В\
и
В
2
соответственно
как
функции
ширины
а\
(в
нм)
более узкой
ямы.
Толщина
барьера
а2
и
ширина
более
широкой
ямы
аз
составляют
2
нм
И
1
О
нм
соответственно.
Времена
жизни
7\1,
722
определяют
соответственно
частоты
внутриподзонных
переходов
для
первой
и
второй подзон
ямы
А,
время
жизни
721 -
частоту
межподзонных
переходов
из
второй
подзоны
ямы
А,
а
характерное
время
утечки
7
0 u
t -
частоту
переходов
из
состояния
А\
в
состояние
В
1
•
Чтобы
поддерживалась
инверсия
населенности
между
уровнями
А
2
и
А\,
время
7
0 u
t
должно
быть мало
по
сравнению
с
721.
Из
работы
[167],
печатается
с
разрешения
Американского
института
физики
244
Гл.
10.
Последние
разработки
Частота
перехода
между
ямами
(пс
-])
0.7
0.6
0.5
0.4
0.3
0.2
0.1
о
5 5.5
6
6.5
б
7 7.5 8
а]
(нм)
Рис.
10.20.
Частоты
переходов
между
ямами
как
функции
ширины
ямы
а]
для
переходов
с
участием
фононов
между
состояниями
А
1
и
В
1
,
вычисленные
на
основе
золотого
правила
Ферми
для
трех
различных
моделей
оптических
фо
нонов,
участвующих
в
процессах
перехода:
штриховая
кривая
а
предполагает
участие
только
объемных
фононов
GaAs,
штриховая
кривая б
предполагает
участие
только
объемных
фононов
A1As,
а
непрерывная
кривая
учитывает
влияние
всего
спектра
оптических
фононных
мод
гетероструктуры.
Как
и на
рис.
10.19,
а2
= 2
нм,
аз
= 10
нм.
Из
работы
[167],
печатается
с
разрешения
Американского
института
физики
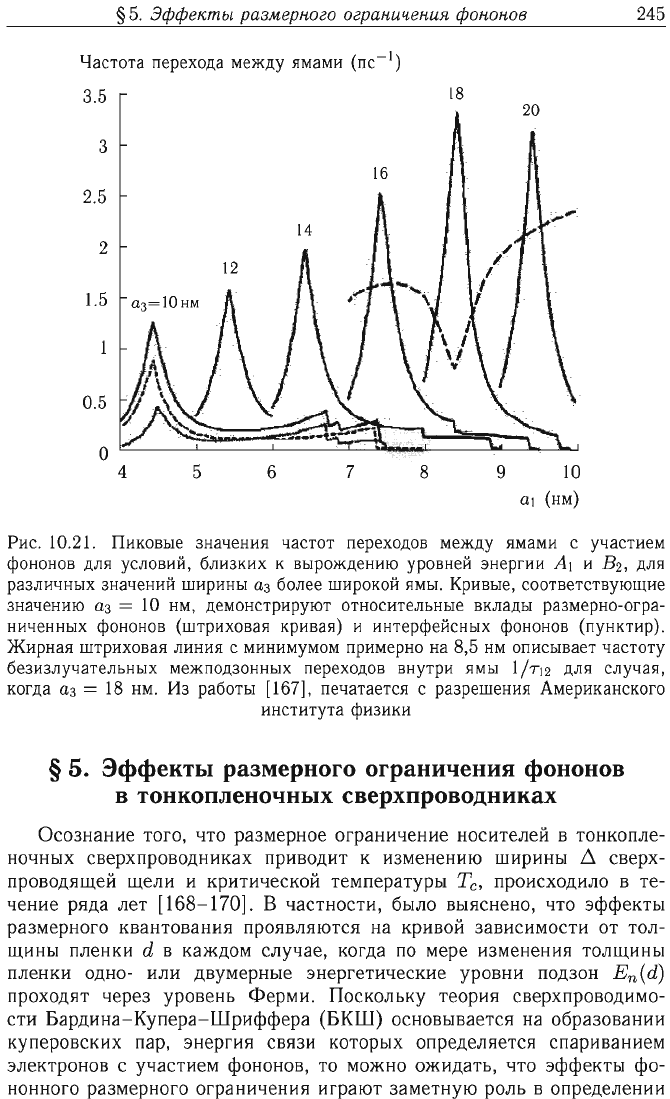
Пиковые
значения
частот
переходов
между
ямами
с
участием
фо
нонов
для
условий,
близких
к
вырождению
энергетических
уровней
А\
и
В
2
,
показаны
на
рис.
10.21
для
разных
значений
ширины
аз
более
широкой
ямы.
При
аз
= 18
нм
частота
переходов
между
ямами
увеличивается
примерно
на
порядок
в
результате
увеличивше
гося
перекрытия
волновых
функций
начального
и
конечного
состояний
вырожденных
уровней
А\
и
В
2
.
Таким
образом, частота
I/T
ou
t
переходов
с
участием
фононов
в
лазерной
структуре
на
межподзонных
переходах
(рис.
10.19)
значи
тельно
увеличивается,
когда
гетероструктура
сконструирована
так,
что
состояния
А\
и
В2
близки
к
вырождению.
В
этом
случае
совмест
ное
применение
метода
конструирования
структуры
зоны
и
метода
управления
фононными
характеристиками
при
водит
к
значительному
увеличению
необходимой
величины
инверсии
населенности
в
лазерах
на
межподзонных
переходах
с
двойными
ямами.
§
5.
Эффекты
разм-ерного
ограничения
фононое
Частота
перехода
между
ямами
(пс"")
245
3.5
3
16
2.5
18
20
2
1.5
0.5
5 6
7
8
9 10
аl
(нм)
Рис.
10.21.
Пиковые
значения
частот
переходов
между
ямами
с
участием
фононов
для
условий,
близких
к
вырождению
уровней
энергии
А
1
и
В
2
,
дЛЯ
различных
значений
ширины
аз
более
широкой
ямы. Кривые,
соответствующие
значению
аз
= 10
нм,
демонстрируют
относительные
вклады
размерно-огра
ниченных
фононов
(штриховая
кривая)
и
интерфейсных
фононов
(пунктир).
Жирная
штриховая
линия
с
минимумом
примерно
на
8,5
нм
описывает
частоту
безизлучательных
межподзонных
переходов
внутри
ямы
1/712
для
случая,
когда
аз
= 18
нм.
Из
работы
[167],
печатается
с
разрешения
Американского
института
физики
§ 5.
Эффекты
размерного
ограничения
фононов
в
тонкопленочных
сверхпроводниках
Осознание
того,
что
размерное
ограничение
носителей
в
тонкопле
ночных
сверхпроводниках
приводит
к
изменению
ширины
Д.
сверх
проводящей
щели
и
критической
температуры
Те,
происходило
В те
чение
ряда
лет
[168-170].
В
частности,
было
выяснено,
что
эффекты
размерного
квантования
проявляются
на
кривой
зависимости
от
тол
щины
пленки
d
в
каждом
случае,
когда
по
мере
изменения
толщины
пленки
одно-
или
двумерные
энергетические
уровни
подзон
Е
n
(d)
проходят
через
уровень
<Dерми.
Поскольку
теория
сверхпроводимо
сти
Бардина-Купера-Шриффера
(БКШ)
основывается
на
образовании
куперовских
пар,
энергия
связи
которых
определяется
спариванием
электронов
с
участием
фононов,
то
можно
ожидать,
что
эффекты
фо
нонного
размерного
ограничения
играют
заметную
роль
в
определении
246
Гл.
10.
Последние
разработки
характеристик
тонкопленочных
сверхпроводников.
В
работе
[171]
недавно
исследована
эта
возможность,
предсказываемая
теорией
БКШ
дЛЯ
тонких
пленок,
путем
замены
объемных
фононов
на
спектр
раз
мерно-ограниченных
фононов
тонких
пленок.
Ожидалось,
что
резуль
таты,
полученные
в
работе
[171],
выявят
определенные
зависимости,
связанные
с
эффектом
размерного
квантования
Фононов
в
тонкопле
ночных
сверхпроводниках,
но не
позволят
делать
точные
количествен
ные
предсказания.
Выявление
только
качественных
характеристик
ожидалось
потому,
что
вычисления
предполагали
бесконечно
высокие
электронные
барьеры
на
границах
пленки
и
в
спектр
фононных
мод
не
были
включены
интерфейсные
фононные
моды.
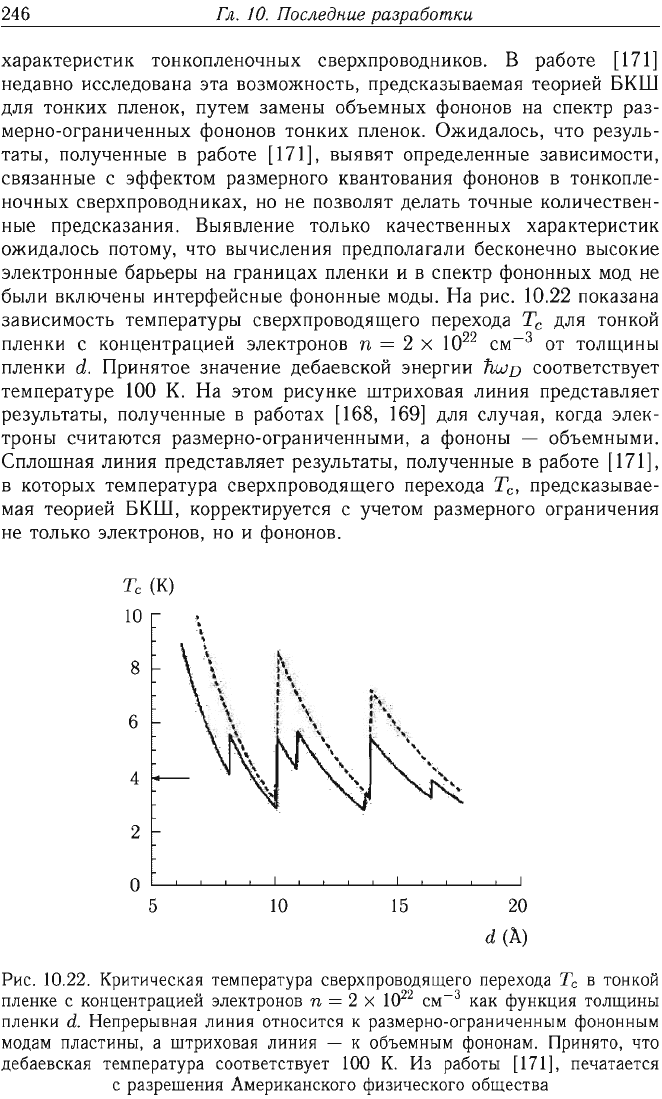
На
рис.
10.22
показана
зависимость
температуры
сверхпроводящего
перехода
Те
для
тонкой
пленки
с
концентрацией
электронов
n = 2
х
1022
см-
З
от
толщины
пленки
d.
Принятое
значение
дебаевской
энергии
n~D
соответствует
температуре
100
К.
На
этом
рисунке
штриховая
линия
представляет
результаты,
полученные
в
работах
[168, 169]
для
случая,
когда
элек
троны
считаются
размерно-ограниченными,
а
фононы
-
объемными.
Сплошная
линия
представляет
результаты,
полученные
в
работе
[171],
в
которых
температура
сверхпроводящего
перехода
Те,
предсказывае
мая
теорией
БКШ,
корректируется
с
учетом
размерного
ограничения
не
только
электронов,
но
и
фононов.
Те
(К)
10
8
6
4
2
О
5
10 15 20
d
(А)
Рис.
10.22.
Критическая
температура
сверхпроводящего
перехода
Те
В
тонкой
пленке
с
концентрацией
электронов
n = 2
х
1022
см-
З
как
функция
толщины
пленки
d.
Непрерывная
линия
относится
к
размерно-ограниченным
фононным
модам
пластины,
а
штриховая линия
-
к
объемным
фононам.
Принято,
что
дебаевская
температура
соответствует
100
К.
Из
работы
[171],
печатается
с
разрешения
Американского
физического
общества

§ 6.
Генерация
акистических
фононов
247
Результаты,
полученные
в
работе
[171],
показывают,
что
эффекты
размерного
ограничения
фононов
играют
важную
роль
в
определении
сверхпроводящих
характеристик
тонкопленочных
сверхпроводников.
Этот
вывод
можно
было
ожидать,
поскольку
тонкопленочные
сверх
проводники
могут
быть
весьма
тонкими,
достигая
размеров
десятков
ангстрем,
и
поскольку
энергия
связи
куперовских
пар
определяет
ся
взаимодействием
электронов
с
фононами.
Для
пленок,
имеющих
толщину,
лежащую
в
диапазоне,
приведенном
на
рис.
10.22,
следует
ожидать,
что
интерфейсные
фононы
будут
также
оказывать
влияние
на
некоторые
свойства
тонкопленочных
сверхпроводников.
§ 6.
Генерация
акустических
фононов
в
структурах
с
квантовыми
ямами
В
работе
[100]
рассчитана
частота
генерации
высокочастотных
размерно-ограниченных
акустических
фононов
в
квантовой
яме
при
взаимодействии
через
деформационный
потенциал
дрейфующих
элек
тронов
и
размерно-ограниченных
акустических
фононных
мод.
Сделано
предположение,
что
дрейфующие
электроны
вызывают
по
механизму
типа
черенковского
эффекта
сильную
генерацию
размерно-ограничен
ных
акустических
фононов
и
коэффициент
усиления
для
этого
про
цесса
как
функция
фононной
частоты
и
параметров,
описывающих
структуру квантовой ямы,
определяются
этими
дрейфующими
элек
тронами.
Коэффициент
усиления
в
несколько
сот
см
"
предсказан
для
р-легированной квантовой
ямы
Si/SiGe/Si
ширины
10
нм.
Чтобы
определить
частоту
генерации размер
но-ограниченных
аку
стических
фононов,
необходимо
вычислить
частоты
рассеяния
элек
тронов
на
размерно-ограниченных
акустических
фононах
в
квантовой
яме
Si/SiGe/Si.
Носители
взаимодействуют
с
акустическими
фононами
через
деформационный
потенциал
Н~~Ф
(5.39):
Н~~Ф
= 6.E
c,v(a)
= Ef,v\J.
и,
(10.33)
где,
как
было
показано
в
п.
6.1
гл.
7,
u(r)
= L
qll'n
(10.34)
Эти
моды
нормируются
в
соответствии
с
выражениями,
приведен
ными
в
§ 1
гл.
5,
где,
однако,
вместо
и
n
(qll' z)
используются
величины
wn (qll' z),
которые,
как
показано
в
приложении
А,
удоб
нее
и
даются
выражением
w
n
=
JPu
n.
Величины
un(qll'
Z)
==
Un,QII
получаются
из
амплитуд
фононных
мод
п.
6.2
гл.
7
путем
деле
ния
на
exp[i(qll . rll -
(.VQ11t)],
поскольку
этот
коэффициент
отдельно
включен
в
вышеуказанное
уравнение для
u(r)
и
в
дельта-функцию,
описывающую
закон
сохранения
энергии
в
золотом
правиле
Ферми.
248
Гл.
10.
Последние
разработки
Понятно,
что
поперечные
моды
не
вносят
вклад
в
деформационный
потенциал.
Два
типа
мод,
рассмотренные
в
§ 2
гл.
7,
содержат
продоль
ные
составляющие:
продольные
моды
и
изгибные
моды.
Продольные
моды
являются
невихревыми
и
связаны
с
искажениями
типа
сжатия
среды;
компрессионный
характер этих
мод
ведет
к
изменениям
локаль
ного
объема
среды.
Как
упоминалось
выше,
в
работе
[125]
выведе
ны
локализованные
акустические
моды
квантовой ямы,
потруженной
в
среду.
Для
симметричной
квантовой
ямы
электроны
спариваются
через
деформационный
потенциал
с
симметричными
сдвиговыми
вер
тикальными
(SSV)
размерно-ограниченными
акустическими
модами.
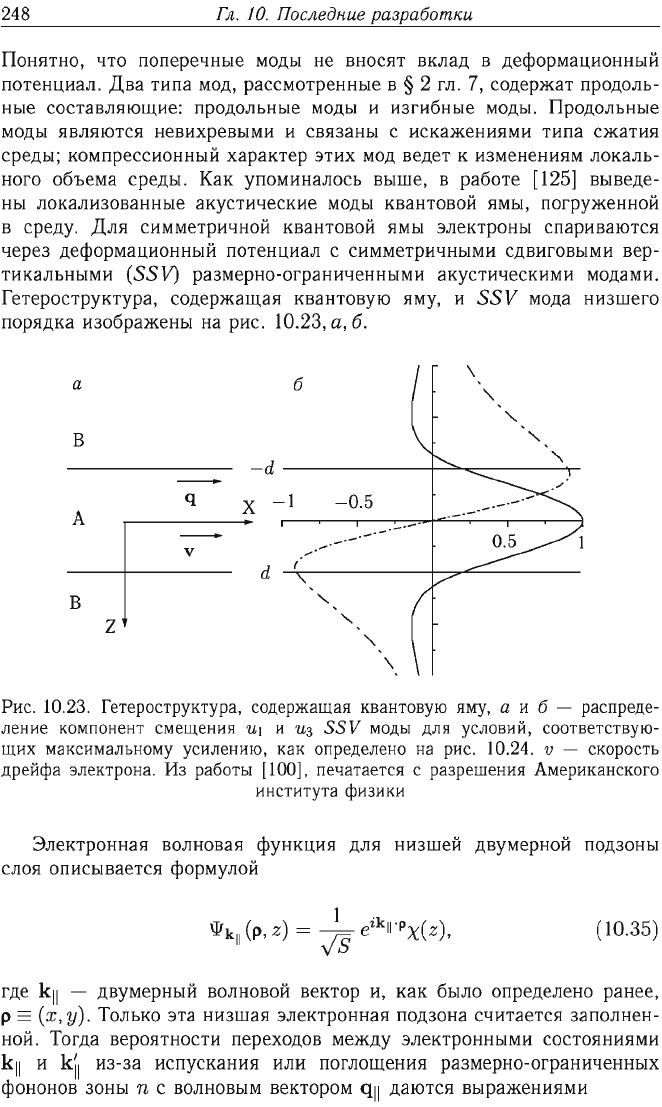
Гетероструктура,
содержащая
квантовую
яму, и
SSV
мода
низшего
порядка
изображены
на
рис.
10.23,
а,
б.
\
-,
-,
\
_.-~
_.--
о-о
-0.5
б
d
q
v
-d
--------1~~-----т
Х
-1
,.-------
г-~-___.-...,....,,::='"'"t""'=--.-__._-~----i
z
а
А
в
в
Рис.
10.23.
Гетероструктура,
содержащая
квантовую
яму,
а
и
б
-
распреде
ление
компонент
смещения
и\
и
UЗ
ssv
моды
для
условий,
соответствую
щих
максимальному
усилению,
как
определено
на
рис.
10.24. v -
скорость
дрейфа
электрона.
Из
работы
[100],
печатается
с
разрешения
Американского
института
физики
Электронная
волновая
функция
для
низшей
двумерной
подзоны
слоя
описывается
формулой
1 "k
,т,
( )
__
~
II'P ( )
~kll
р,
Z -
vs
е
Х
z ,
(10.35)
где
k
ll
-
двумерный
волновой
вектор
и,
как
было
определено
ранее,
р
==
(х,
у).
Только
эта
низшая
электронная
подзона
считается
заполнен
ной.
Тогда
вероятности
переходов
между
электронными
состояниями
k
ll
и
kil
из-за
испускания
или
поглощения
размерно-ограниченных
фононов
зоны
n
с
волновым
вектором
Ч]
даются
выражениями

§6.
Генерация
акистических
фононов
249
(±),
27Г
2 ( 1
1)
Р
(kll,k11In,qll)=TIM(q)1
nn,qll+
/2±
/2
8kxH,k~8ky,k~X
Х
8
(E(k
ll)
-
E(k
ll)
т
n'VJ)
F(k
ll)
[1
-
F(k
l
l)]
,
(10.36)
где
00
M(q) =
kэ~[q)
fV'.
Un,q
X
2(z)
dz,
-00
(10.37)
(10.39)
-
(+)
-
(-)
'Yn,QII
-
'Yn,QII
'Yn,QI
I'
nn,qll -
число
заполнения
фононов
моды
{n,qll},
kЭЛ(q)
-
электрон
ная
проницаемость,
описанная
в
приложении
Е
[172, 100],
F(k
ll)
=
=
F(k
x,
k
y)
-
функция
распределения
электронов,
а
q = Iqlll.
в
прило
жении
Е
приведен
вывод
выражения
для
kЭЛ(q),
основанный
на
методе
Линдхарда,
примененном
к
двумерному
электронному
газу
[172].
Для
определения
результирующей
частоты
генерации
локализован
ных
акустических
фононов
в
работе
[100]
рассмотрено
уравнение
dnn,qll _
(+)
( ) _
(-)
_
dt -
'Yn,qll
1 + nn,qll
'Yn,QII
nn,QII
,8n,QII
nn,QII
' (10.38)
где
коэффициенты
'Y~~JII
определяются
путем
вычисления
полных
ча
стот
поглощения
и
испускания
фононов
для
моды
{n, Qll}'
а
,8n,QII
опи
сывает
потери
фононов,
такие
как
неэлектронное
поглощение
фононов
или
ангармонический
распад
фононов.
Определяя
фононный
инкремент
формулой
получаем
выражение
'Yn,QII
=
n~;q
IM(q)1
2
[j(+)(q) - j(-)(q)] ,
где
m* -
эффективная
масса
и
(10.40)
00
*
(±)
()
f
((
. )
т
VJn,QII
1/
)
j q =
dkyF
Slgnq n'lql ± 2 q, k
y
.
-00
(10.41)
Для
случая,
когда
внешнее
электрическое
поле
заставляет
электроны
дрейфовать
со
скоростью
Vdr,
принимая
функцию
распределения
элек
тронов
в
виде
смещенного
распределения
Ферми
Рр,
получаем
F(kx,k
y)
=
Рр
(k
x
-
~*
Vdr,k
y).
(10.42)
Отсюда
следует,
что
(ln,QII
=
'Yn,QII/V
g
>
О,
если
скорость
дрейфа
электронов
превышает
фазовую
скорость
размерно-ограниченных
фононов:
V
dr
>
VJn,q/lql,
где
групповая
скорость
фононов
~
=
dVJn,q/dq.

250
Гл.
10.
Последние
разработки
Это
условие
аналогично
критерию
для
черенковского
излучения.
В
работе
[100]
вычислена
величина
a
n
•
QII
для
двух
низших
SSV
фононных
ветвей
р-легированной квантовой
ямы
Si/SiGe/Si
толщины
10
нм.
Коэффициенты
усиления
для
этих
фононных
ветвей
показаны
на
рис.
10.24
для
температуры
Т
= 50, 100, 150
и
200
К.
В
этих
численных
расчетах
плотность
дырок
предполагалась
на
уровне
1012
см-
2
,
скорость
дрейфа
дается
выражением
Vdr
= 2,
5Ct1,
где
Ctl
=
3,4
см/с
для
слоя
SiGe.
468
qd
а/О'тах
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0.0
О
2
4
6
10
8
6
8 10 12
w/wo
Рис.
10.24.
Безразмерный
коэффициент
усиления
фононов
а/а
m
а
х
как
функ
ция
фонанной
частоты
w/wo
для
двух
низших
SSV
фононных
ветвей.
Т
=
=
50, 100, 150
и
200
К;
чем
больше
значение
Т,
тем
ниже
значение
а.
Скшах
= 290
см
";
Wo
= 110
ГГц.
На
вставке
изображены
значения
W/Wo
как
функции
qd
для
максимумов
а
при
температуре
Т
= 50
К.
Из
работы
[100],
печатается
с
разрешения
Американского
института
физики
Видно,
что
коэффициент
усиления
в
суб-терагерцевом
диапазоне
частот
размерно-ограниченных
мод
этой
р-легированной
квантовой
ямы
Si/SiGe/Si
составляет
от
десятков до
сотен
CM-
1.
