Строшио М., Дутта М. Фононы в наноструктурах
Подождите немного. Документ загружается.


§ 1.
Фононные
эффекты
в
лазерах
221
LО-моды
полу
пространства
в
полярном
сплаве
3 (i =
о,
i = 3)
имеют
вид
{
.
2m7Г
(
Ь)
SШ
L
z+"2 '
ф(Z)
сх
.
2m7Г
(
а)
sш--
Z--
L
2'
т
=
1,2,3,
...
,
т
=
1,2,3,
...
,
Ь
z:<
--
"" 2
(10.3)
Кроме
того,
имеются
интерфейсные
LО-фононные
моды, такие
как
в
п.
3.4
гл.
7,
которые
имеют
вид
фi(q,
Z)
сх
c~_q-qz
+
c~+q+qz,
(10.4)
где
значения
c~±
определяются
граничными
условиями
c~_
=
о,
I -
О
С
З
+
- ,
Фl(q,z=
-L/2)
=0
===?
фз(q,
Z =
-L/2)
=
О
===?
Фi(
q, Zi) =
Фi-l
(q,Zi),
дФi
(q, Zi)
дФi-l
(q, Zi)
E:i
az
=
E:i-l
az
.
(10.5)
Здесь
величина
L
выбирается
достаточно
большой
по
сравнению
с
другими
пространственными
масштабами
в
системе,
а
Zi
обозначает
координату
z,
соответствующую
положению
поверхности
раздела
между
областями
i
и
i - 1.
Условия
непрерывности
потенциала
и
непре
рывности
нормальной
составляющей
электрической
индукции
могут
быть
использованы
для
того,
чтобы
рекуррентно
связать
ненулевые
ко
эффициенты
c~±
с
диэлектрическими
постоянными
различных
веществ,
составляющих
гетероструктуру.
Граничное
условие
при
Z =
L/2
требу
ет,
чтобы
<3+
=
о,
а
дисперсионное
соотношение
для
интерфейсных
мод
гетероструктуры,
приведенной
на
рис.
10.2,
а,
имеет
следующий
вид:
0=
_1_
[(Е:З
-
Е:l)(Е:l
+
Е:2)(Е:2
-
Е:З)
e-q(аН)
+
Е:IЕ:2Е:з
+
(Е:з
-
Е:l)(Е:l
-
Е:2)(Е:2
+
Е:з)
e-
2qa
+
+
(Е:З
+
Е:l)
(Е:l
-
Е:2)
(Е:2
-
Е:З)
e-q(b-a)
+
+
(Е:З
+
Е:l)(Е:l
+
Е:2)(Е:2
+
Е:З)],
(10.6)
где
обобщенное
соотношение
Лиддейна-Сакса-
Теллера
используется
для
выражения
E:n(W)
через
Е:n(ОО).
Из
уравнений
(7.5), (7.6)
следует,
что
для
бинарных
соединений
(10.7)
222
Гл.
10.
Последние
разработки
(10.8)
I I I I I
а
для
трехкомпонентных
сплавов
вида
AyB1-уС
(
U;
2
u;2
) (u;2
u;2
)
.::n(u;) =
'::n(ОО)
- LO,n,a - LO,n,b ,
u;2
-
u;2 u;2
-
u;2
ТО,n,а
ТО,n,Ь
где,
как
обсуждалось
в
§ 1
гл.
7,
индекс
а
обозначает
частоты,
свя
занные
с
дипольными
парам
и
АС,
а
индекс
Ь
-
частоты,
связанные
с
дипольными
парам
и
ВС.
Условие
c;+(u;) =
О
выполняется
для
10
частот
и,
соответственно,
существуют
10
интерфейсных
мод:
шесть
из
них
соответствует
модам
типа
мод
GaAs
с
энергиями
в
диапазоне
от
32
до
37
мэБ,
а
четыре
являются
модами
типа
мод
AIAs
с
энергиями,
близкими
к
46
мэБ.
Дисперсионные
соотношения
для
этих
10
мод
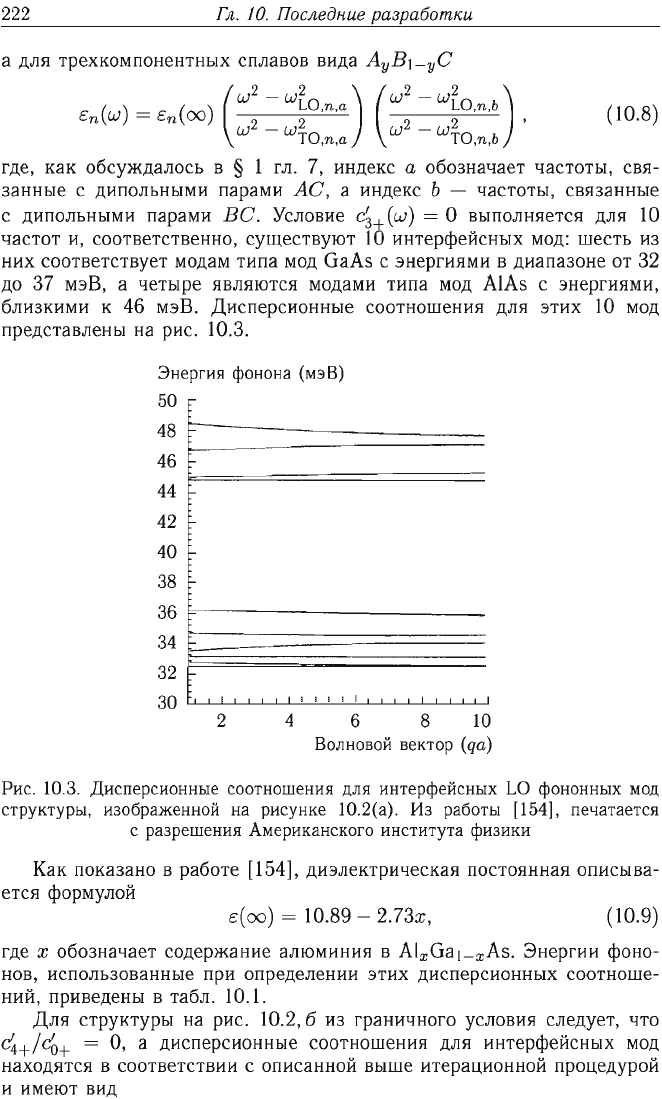
представлены
на
рис.
10.3.
Энергия
фонона
(мэВ)
50
48
46
44
42
40
38
36
34
32
30
2 4 6 8 10
Волновой
вектор
(qa)
Рис.
10.3.
Дисперсионные
соотношения
для
интерфейсных
LO
фононных
мод
структуры,
изображенной
на
рисунке
10.2(а).
Из
работы
[154],
печатается
с
разрешения
Американского
института
физики
Как
показано
в
работе
[154],
диэлектрическая
постоянная
описыва
ется
формулой
'::(00)
= 10.89 -
2.73х,
(10.9)
где
х
обозначает
содержание
алюминия
в
AlxGal-хАs.
Энергии
фоно
нов,
использованные
при
определении
этих
дисперсионных
соотноше
ний,
приведены
в
табл.
10.1.
Для
структуры
на
рис.
10.2,
б
из
граничного
условия
следует,
что
c~+/c~+
=
О,
а
дисперсионные
соотношения
для
интерфейсных
мод
находятся
в
соответствии
с
описанной
выше
итерационной
процедурой
и
имеют
вид

§ 1.
Фононные
эффекты
в
лазерах
223
-
(Ез
+
Е2)2(Е2
-
Е1)2
e
2qa
+
(Ез
+
Е2)2(Е1
+
Е2)2]
,
(10.10)
Четырнадцать
решений
этого
уравнения
соответствуют
шести
интер
фейсным
модам
типа
мод
GaAs
и
восьми
интерфейсным
модам
типа
мод
AIAs.
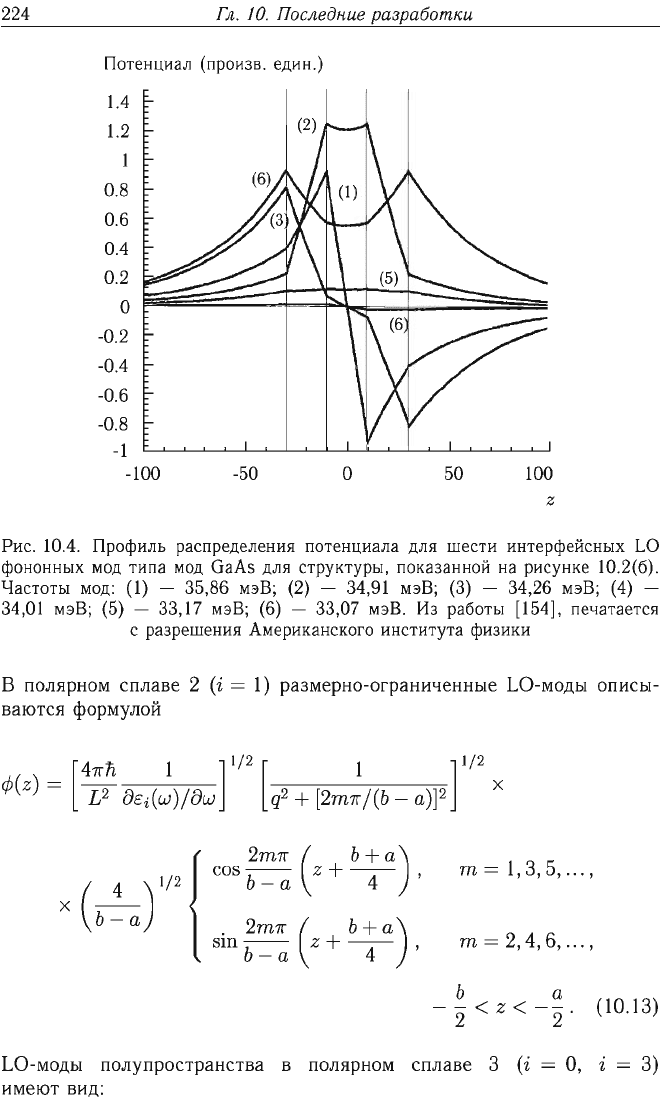
Потенциалы
для
шести
мод
типа
мод
GaAs
приведены
на
рис.
10.4
для
qa = 0,5.
Эти
LО-фононные
моды
являются
либо
симметричными,
либо
анти
симметричными,
как
и
следует
ожидать
из
симметрии
гетерострукту
ры, и
их
необходимо
еще
отнормировать.
Условие
нормировки
(7.116)
п.
3.4
гл.
7
,,_1
_1
дEi(VJ)
fd
{2
I
ф
.
(
)12
I
дФi(q,
z) 1
2
}
=
_n_
LJ
47Г
2VJ
aVJ
z q
ъ
q, Z + az
2VJL2
'
i
R,
(10.11)
дает
возможность
определить
нормировочные
постоянные
для
каж
дой
моды
и
приводит
К
следующим
нормированным
потенциалам
LО-фононов.
В
полярном
полупроводнике
1 (i = 2)
размерно-ограни
ченные
LО-моды
описываются
формулой
[
4
7Г
n
1 ]
1/2
[ 1 ]
1/2
Ф(z)
=
L2
дEi(VJ)/aVJ
q2
+
(m7Г/а)2
х
{
m7Г
/
cos-z,
х
Ш
1 2
вш
~п
z,
т
=
1,3,5,
...
,
т
=
2,4,6,
...
,
а
Izl
<
:2'
(10.12)
т
а
б
л и
ц
а
10.1.
Значения
энергий
фОНОНОВ,
принятые
В
расчетах
Энергия
фонона
GaAs
(мэВ)
nVJLO,a
36.25
nVJLO,b
nVJTO,a
33.29
nVJTO,b
AIAs
50.09
44.88
36.25 -
6.55х
+
1.79х
2
44.63 +
8.78х
-
3.32х
2
33.29 -
0.64х
-
1.16х
2
44.63 +
0.55х
-
0.зох
2
224
Гл.
10.
Последние
разработки
Потенциал
(произв.
един.)
1.4
1.2
1
0.8
0.6
0.4
0.2
О
-0.2
-0.4
-0.6
-0.8
-1
-100 -50
О
50 100
z
Рис.
10.4.
Профиль
распределения
потенциала
для
шести
интерфейсных
LO
фононных
мод
типа
мод
GaAs
для
структуры,
покаванной
на
рисунке
10.2(6).
Частоты
мод:
(1) -
35,86
мэБ;
(2) - 34,91
мэБ;
(3) - 34,26
мэБ;
(4) -
34,01
мэБ;
(5) - 33,17
мэБ;
(6) - 33,07
мэБ.
Из
ра60ТЫ
[154],
печатается
с
разрешения
Американского
института
физики
в
полярном
сплаве
2 (i = 1)
размерно-ограниченные
LО-моды
описы
ваются
формулой
[
4-
7Г
п'
1 ] 1/2 [ 1 ] 1/2
ф(z)
= L2
дEi(UJ)/aUJ
q2
+
[2m1Г/(Ь
_
а)р
х
2m1Г
(
ь+а)
cos
Ь
_
а
z +
-4-
,
.
2m1Г
(
Ь
+
а)
sш
Ь
_
а
z +
-4-
,
m=1,3,5,
... ,
т
= 2,4,6, ... ,
Ь
а
-"2<z<-"2'
(10.13)
LО-моды
полупространства
в
полярном
сплаве
3 (i =
О,
i = 3)
имеют
вид:

§ 1.
Фононные
эффекты
в
лазерах
[
4
7Г
п
1 ]
1/2
[ 1 ]
1/2
ф(z)
=
L2
дE:i(w)/aw
q2
+ (2mn/L)2
х
225
{
2m7Г
(
Ь)
х
i
1/2
СОБ
L z
+"2
'
(L)
sin
2m~
(z
_
~)
L
2'
т
=
1,2,3,
... ,
т
=
1,2,3,
... ,
Ь
z:O:::
--
'"
2'
(10.14)
Как
показано
в
п.
3.4
гл.
7,
потенциалы
интерфейсных
LО-фононных
мод
имеют
следующий
вид
(см.
уравнения
(7.117), (7.118)):
Фi(q,
z) =
А(с~_е-qZ
+
c~+e+qZ)
= AWi(q, z),
(10.15)
где
нормировочная
постоянная
А
дается
формулой
А
=
(_п
)
1/2
("
_1
_1
дE:i(w)
х
2wL2 6
47Г
2w aw
~
х
1.
dz
{q'lф,(q.
z)I' +
11fф~;·
')
1'}
)
-1/'.
(10 16)
Окончательно
из
уравнения
(7.119)
получаем
HIF
=
еФi(Г)
=
е
L
e-iq·РФi(q,
z)(a~q
+ a
q)
=
q
=
е
L
e-
iq.
p
AWi(q,
z)(a~q
+ a
q).
(10.17)
q
Для
отдельной
фононной
моды
j
фрёлиховский
гамильтониан
вза
имодействия
имеет
вид
H
j
=
ефj(Г)
=
е
L
e-iq'РФj(г)(а~q
+ a
q),
q
(10.18)
и
из
§ 1
гл.
8
следует
S~~~~}(k,
k')
=
2:
L
IM~~~}(q)12
8(E(k') +
Е
n
,
- E(k) -
е;
± hw),
q
(10.19)
где
M~~~~}(q)
= (n',k', N
q
+
1/2
±
1/21
H
j
1
п,
k, N
q
+
1/2
± 1/2)
(10.20)
8
М.
А.
Сторшио,
М.
Дутта

226
Гл.
10.
Последние
разработки
и
где
начальная
и
конечная
энергии
были
записаны
в
виде
суммы
E(k)
+
Е
n
кинетической
энергии
E(k)
=
1i
2
k
2
/2m
и
энергии
подзоны
Е
n
.
Поскольку
кинетическая
энергия,
связанная
с
двумерным
волно
вым
вектором
k,
была
отделена
от
энергии
подзоны,
нижний
индекс
2D,
используемый
в
§ 1
гл.
8,
опущен.
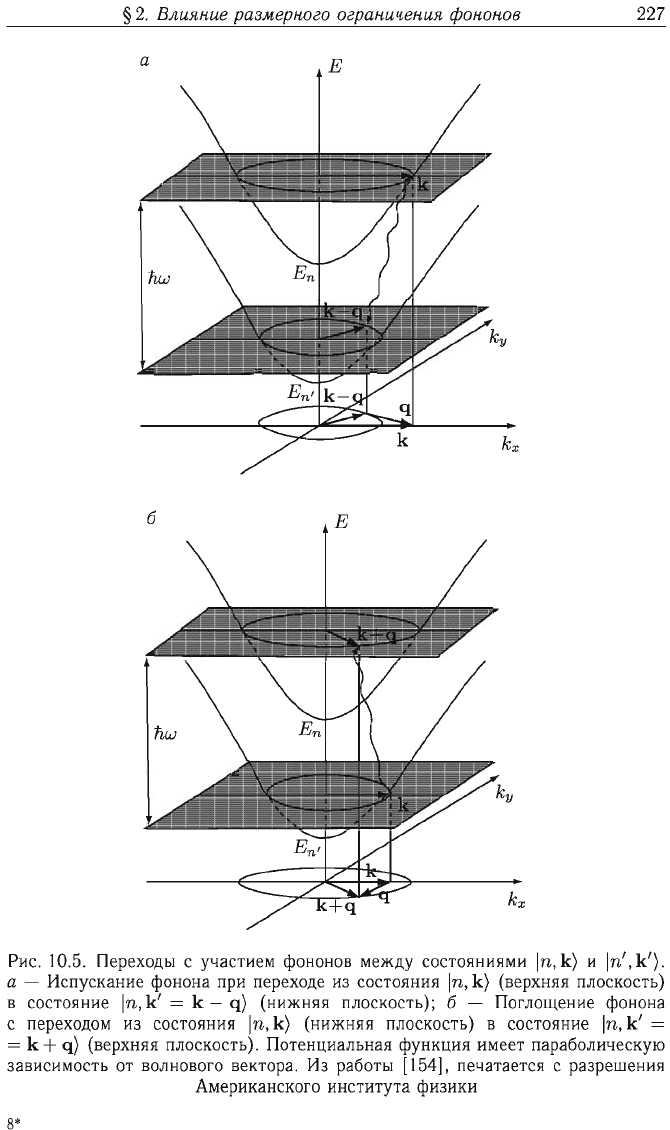
Переходы
носителей
между
начальным
и
конечным
состояниями
с
участием
фононов
изображены
на
рис.
10.5.
В
работе
[154]
численно
решено
уравнение
Шредингера
и
опре
делены
волновые
функций
электрона
определенных
фононных
мод,
необходимых
для
вычисления
матричных
элементов
переходов
с
уча
стием
фононов.
Акцент был
сделан
на
процессе
испускания
фо
нонов,
важном
для
углубленного
понимания
фононных
процессов
в
полупроводниковых
лазерах
с
узкими
ямами.
Как
и
ожидалось
[156],
результаты
этих
работ
показывают,
что
моды
полупространства
и
размерно-ограниченные
LО-моды
дают
частоты
фононных
переходов,
которые
малы
по
сравнению
с
частотами,
связанными
с
интерфейс
ными
LО-фононными
модами.
Кроме
того,
обнаружено,
что
некоторые
интерфейсные
моды
вносят
вклад,
примерно
на
порядок
больший,
чем
большинство
других
интерфейсных
LО-фононных
мод.
На
рис.
10.6
показан
при
мер
доминирующего
фононного
перехода
в
симметричной
структуре,
изображенной
на
рис.
10.2,
б.
Максимальная
частота
соот
ветствует
переходу
с
испусканием
антисимметричного
интерфейсного
LО-фонона
с
энергией,
близкой
к
50
мэВ.
Из
рис.
10.6
с
очевидностью
следует,
что
эта
частота
существенно
больше
частоты
испускания
объемных
фононов.
Отсюда
ясно,
что
в
конструкции
полупроводнико
вых
лазеров
с
узкими
ямами
важно
учитывать
интерфейсные
моды.
Обычное
приближение,
в
котором
все
фононы
считаются
объемными,
является
неадекватным.
§ 2.
Влияние
размерного
ограничения
фононов
на
коэффициент
усиления
лазеров
на
межподзонных
переходах
В
предыдущем
параграфе
было
продемонстрировано,
что
в
полу
проводниковых
наноструктурных
лазерах
на
межподзонных
перехо
дах
важно
учитывать
спектр
размерно-ограниченных
фононных
мод.
В
этом
пара
графе
будет
показано,
что
усиление
полупроводниково
го
лазера
на
межподзонных
переходах
с
узкими
ямами
можно
точ
но
рассчитать,
только если
принимать
в
расчет
реальный
спектр
фононов
гетероструктуры
[155].
Система,
рассмотренная
при
вычис
лении
коэффициента
усиления
лазера
на
межподзонных
переходах
с
квантовыми
ямами,
представляет
собой
двойную
гетероструктуру
AlxGal-хАs/GаАs/
AlxGal-хАs
толщины
а.
Волновые
функции
элек
трона
и
дисперсионные
соотношения
для
этой
системы
получены
[155]
§2.
Влияние
разм-ерного
ограничения
фононое
227
а
Е
б
Е
Рис.
10.5.
Переходы
с
участием
фононов
между
состояниями
In,
k)
и
In',
k').
а
-
Испускание
фонона
при
переходе
из
состояния
In,
k)
(верхняя плоскость)
в
состояние
In,
k'
= k - q)
(нижняя
плоскость);
б
-
Поглощение
фонона
с
переходом
из
состояния
In,
k)
(нижняя
плоскость)
в
состояние
In,
k'
=
=
k +
ч)
(верхняя
плоскость).
Потенциальная
функция
имеет
параболическую
зависимость
от
волнового
вектора.
Из
работы
[154],
печатается
с
разрешения
Американского
института
физики
8*

228
Гл.
10.
Последние
разработки
Максимальные
частоты
перехода
(с
-1
)
3.0x10
13
2.5 x10
13
2.0x10
13
1.5x10
13
1.0x10
13
5.0x10
12
40 50
БО
70 80 90 100
Е
2
-
Е
1
(мэБ)
Рис.
10.б.
Зависимость
максимальных
частот
переходов
для
ангисиммегричной
интерфейсной
моды
и
для
объемной
моды
от
разности
конечной
и
начальной
энергии
носителя,
рассчитанные для
симметричной
гетероструктуры,
приве-
денной
на
рис.
10.2,
б
по
четырехзонной
модели
Кане.
Электронные
волновые
функции
со
стояний
[159]
в
подзоне
n
взяты
в
виде
(10.21)
где,
как
и
выше,
р
=
(х, У),
а
S -
площадь
гетероструктуры.
В
лазерах
на
межподзонных
переходах,
например
лазерах
на
квантовых
каска
дах,
переходы
происходят
только
в
зоне
проводимости
и
огибающие
четырехкомпонентной
волновой
функции
Кане
'Ф~n)
могут
быть
выра
жены
просто
в
виде
скалярных
волновых
функций.
Для
самой
нижней
подзоны
(n = 1)
приближенные
волновые
функции
имеют
вид
где
cos
kz1Z,
kz1a
-ЛI(lzl-а/2)
cos 2
е
,
а
Izl
<"2'
а
Izl
>"2'
(10.22)
(10.23)

§2.
Влияние
разм-ерного
ограничения
фононое
Для
второй
подзоны
(n = 2)
эти
функции
имеют
вид
229
где
sin k
z21
Z ,
sign z sin k
z2
a
e-Л2Сlzl-а/2)
2 '
а
Izl
<"2'
а
Izl
>"2'
(10.24)
(10.25)
Здесь
E
wn
и
Еьn
-
энергии
n-й
подзоны
ямы
и
барьера
соответ
ственно,
измеряемые
относительно
валентной
зоны
в
соответствующей
среде.
Очевидно,
что
для
волновых
функций
приведенного
вида
пере
ходы
с
участием
фононов
из
второй
подзоны
в
самую
нижнюю
будут
осуществляться
только
с
участием
антисимметричных
интерфейсных
фононов,
нечетных
размерно-ограниченных
фононных
мод
и
барьерных
мод.
Однако
внутриподзонные
переходы
с
участием
фононов
будут
включать вклады
симметричных
интерфейсных
фононов,
четных
раз
мерно-ограниченных
фононных
мод
и
барьерных
мод.
Как
будет
пока
за
но
ниже,
такие
процессы
с
участием
фононов
приводят
к
эффекту
уширения
линии,
что
оказывает
большое
влияние
на
усиление
лазера.
Кроме
того,
станет
очевидным,
что
зависимость
уширения
линии
от
энергии,
определяемая
энергетическим
спектром
фононов,
также
игра
ет
значительную
роль
в
определении
коэффициента
усиления
лазера.
Кривые
дисперсии
энергии
подзоны
для
квантовых
ям
ширины
60
А
и
1О0А
изображены
на
рис.
10.7
вместе
с
примерами
межподзонных
и
внутриподзонных
процессов
с
участием
фононов.
На
рис.
10.7
пара
метр
х
=
0,3,
а
де
=
300
мэБ
и
д
v
= 150
мэБ
для
зоны
проводимости
И
валентной
зоны
соответственно.
Спектр
фононов,
использованный
в
вычислении
межподзонного
оптического
усиления
в
рассматриваемой
квантовой
яме,
включает
в
себя
симметричные
интерфейсные
моды,
антисимметричные
интер
фейсные
моды,
две
размерно-ограниченные
моды
низшего
порядка
и
моды
полупространства.
которые
в
настоящем
параграфе
называются
барьерными
модами.
Гамильтонианы
фрёлиховского
взаимодействия,
использованные
здесь,
являются
соответствующими
гамильтонианами
модели
диэлектрического
континуума
с
электростатическими
гранич
ными
условиями,
как
это
описано
в
гл.
7
и
в
приложении
Б.
Эти
моды
можно
непосредственно
получить
из
мод
двойной
гетеро
структуры,
рассчитанных
в
приложении
Г
для
одноосной
среды,
если
перейти
к
пределу,
в
котором
как
E(W)..l'
так
и
E(W)II
равны
E(W).
На
рис.
10.8,
а,
6
и
10.9,
а,
6
изображены
частоты
рассеяния
мод,
вносящих
основной
вклад
[155],
для
представленных
выше
скалярных
волновых
функций
и
для
фононных
мод
модели
диэлектрического
континуума
с
электростатическими
граничными
условиями.
230
Гл.
10.
Последние
разработки
,-
/
/
/
/
/
/
" /
,," /
;'
/
<с.:
/
"
"
"
"
;'
;'
;'
...-
---
100
200
Энергия
подзоны
(мэВ)
300
2 3
4
5
6
ka
Рис.
10.7.
Дисперсионные
кривые
энергии
для
квантовых
ям
шири
ной
60
А
(сплошные
линии)
и
100
А
(пунктирные
линии)
гетереструктуры
Аlо.зGао.7Аs/GаАs/
Аlо.зGао.7Аs.
Типичные
межподзонные
и
внутриподзонные
переходы
показаны
стрелками.
Энергетическая
щель
E
g
для
ямы
GaAs
при
нята
равной
1,4
эВ,
а
отношение
эффективной
массы
к
массе
электрона
для
GaAs - 0,067.
Из
работы
[155],
печатается
с
разрешения
Американского
института
физики
в
этих
вычислениях
были
приняты
следующие
параметры:
х
= 0,4,
~c
= 300
мэВ,
~v
= 200
мэВ,
а
= 60
А.
Энергетический
спектр
на
рис.
10.8,
а
четко
демонстрирует
существование
нескольких
различных
порогов.
Спектр
оптического
усиления
g(П)
при
переходах
между
второй
и
низшей
подзонами
[160,
159]
дается
выражением
(10.26)
где
форма
линии
описывается
функцией
(10.27)
энергия
перехода
связана
с
разностью
пЛ
о
энергий
подзон
при
k =
О
выражением
(10.28)
