Строшио М., Дутта М. Фононы в наноструктурах
Подождите немного. Документ загружается.


Приложенив
В
261
(В.10)
Это
равенство
прямо
следует
из
условия
Ч]
= q.
Как
показано
в
гл.
5,7,
потенциал
взаимодействия
для
этих
нормированных
мод
записывается
в
виде
Фm(Г)
= L
Фm(q,
z)
e-
iq
.
p
.
q
Решения
в
виде
W = -
\7х,
удовлетворяющие
этим
уравнениям
Эйлера
Лагранжа,
имеют
вид
(В.11
)
и
1
Ф
= -
(c.Jto
-
c.J2)X
+
М\72
х
-
Во
(В.12)
'у
для
интервала О
< z < d,
где
М
=
А
+
В
+
С
и
ВО
-
постоянная.
Вне
пластины
потенциал
Ф
удовлетворяет
уравнению
Пуассона.
Как
было
показано
выше,
поля
пластины
проявляют
трансляционную
инвариант
ность
в
направлении,
нормальном
к
поверхности
пластины;
поэтому
x(r)
=
X(z)
exp[iq
.
р]
и
Ф(г)
=
ф(z)
exp[iq
.
р],
где
q
и
р
определены
выше.
Таким
образом,
если
q
t=-
о,
то
ВО
=
о.
Тогда
два
последних
уравнения
можно
записать
как
и
(В.13)
(В.14)
соответственно.
Нэш
применил
метод,
используемый
при
анализе
урав
нения
Штурма-Лиувилля,
чтобы
показать,
что
решения
в
виде
нор
мальных
мод пластины
должны
удовлетворять
следующим
граничным
условиям:
ФФ'
=
о
(В.15)
при
z =
±оо
и
Ш
Х
=
Ш
у
=
ш~
=
О
или
ШхШ~
+
ШуШ~
+ W
z
=
О
(В.16)
при
z =
О
и
при
z = d.
Положив,
как
и
выше,
W = -
\7х,
сведем
уравнения
(В.16)
к
виду
Х
=
х"
=
о
и
х'
=
о
(В.17)
соответственно.
В
этом
месте
поучительно
рассмотреть
каждый
из
обычно
исполь
зуемых
наборов
нормальных
мод
и
сравнить
граничные
условия,
которым
они
удовлетворяют,
с
условиями,
полученными
в
рамках

262
Приложения
уравнения
Штурма-Лиувилля.
Нэш
в
уравнении
четвертого
порядка
дЛЯ
X(Z)
положил
k~q
=
(UJ[o
-
UJ2)/(J-l
-
q2)
и
пришел
к
уравнению
четвертой
степени
для
собственных
значений:
(В.18)
где
k~q
-
собственное
значение
Xnq(Z)
и
где
нижние
индексы
n
и
q
определяют
различные
члены
базисного
набора.
Как
обычно,
q
обозначает
волновой
вектор
в
плоскости
ху,
а
целочисленный
индекс
п
нумерует
разные
моды
с
одинаковой
величиной
q.
Именно
это
уравне
ние
Нэш
использовал
для вывода
полного
набора
ортонормированных
функций,
представляющих
фононные
моды.
Как
было
показано
в
гл.
7,
условие
ортогональности
нормальных
мод
дается
выражением
для
СУ
-=1-
(3,
(В.19)
где
каждый
индекс
СУ
и
(3
обозначает
совокупность
квантовых
чисел
nq.
С
учетом
того
что
w =
-\7х
и
х(г)
= x(z)exp[iq·
р],
это
условие
ортогональности
можно
записать
в
виде
d
* 1 f 2 *
dX~q
dXn'q'
Xnq
.
Xn'q'
= 2d dz q
Xnq(Z)
. Xnq(z) +
----а:;-
~
.
о
(В.20)
(В.21
)
. (n +
1)7ГZ
Xnq(z) =
sш
d '
Различные
виды
ограниченных
интерфейсных
оптических
фоно
нов,
которые
приведены
в
литературе,
включают
так
называемые
мо
ды
пластины,
которые
удовлетворяют
электростатическим
граничным
условиям,
моды
Хуан
Куня-Жу,
основывающиеся
на
комбинировании
(переразложении)
мод
пластины,
и
так
называемые
волноводные
моды,
которые
удовлетворяют
механическим
граничным
условиям.
Для
мод
пластины
граничные
условия
для
величины
Xnq(Z)
при
Z =
О
и
при
Z = d
имеют
вид
Xnq
=
X~q
=
О,
и
для
получения
полного
набора
мод
необходимо
добавить
интерфейсные
моды.
Электростатические
потенциалы
Фnq
для
этих
мод даются
выражением
47Г'У
Фnq
= -
Е(ОО)
Xnq(Z).
(В.22)
Нормальные
моды,
удовлетворяющие
уравнению
ФФ'
=
о
при
Z =
±оо
и
условиям
Х
=
х"
=
о
при
Z =
О
и
при
Z = d,
представляют
собой
моды
пластины.

Приложенив
В
263
Для
комбинированных
мод
Хуан
Куня-Жу,
приведенных
Нэшем,
{
COSl-Lnqнz'/d+Dnqсhqz',
п
четное,
Xnq(z) =
(В.23)
sin
I-L
n
qJrZ'
/ d + D
nq
sh qz', n
нечетное,
граничные
условия
для
величины
Xnq(Z)
при
Z =
О
и
z = d
имеют
вид
Xnq
=
X~q
=
О,
и
для
получения
полного
набора
мод
необходимо
добавить
интерфейсные
моды.
Моды
Хуан
Куня-Жу
были
введены
для
того,
чтобы
удовлетворить
этим
граничным
условиям
на
поверхностях.
На
практике,
граничные
условия
Xnq
=
X~q
=
о
удовлетворяются
по
средством
выбора
необходимых
значений
D
nq
и
I-Lnq'
Моды
Хуан Куня
Жу
часто
называют
комбинированными
модами
пластины,
а
также
комбинированными
модами
континуальной
диэлектрической
модели
(с
электромагнитными
граничными
условиями).
Хуан
Кунь
и
Жу
[190]
показали,
что
моды
бездисперсионной
микроскопической
теории при
малом
значении
q
хорошо
аппроксимируются
этими
комбинированными
модами
пластины.
Электростатические
потенциалы
Фnq
для
этих
мод
описываются
выражением
47Г1'
Фnq
= -
10(00)
Xnq(Z).
Для
волноводных
мод
(В.24)
nJrz
Xnq(Z)
= cos
Т'
(В.25)
граничные
условия
для
величины
Xnq
(z)
при
z =
О
и
z = d
имеют
вид
X~q
=
X~q
=
о
и,
как
указано
Нэшем,
для
получения
полного
набора
мод
нет
необходимости
добавлять
интерфейсные
моды.
Для
этих
мод
электростатические
потенциалы
даются
формулами
47Г1'
{
cosnJrz/d-е-qdj
2сhq(z-d/2),
Фnq(Z)
=
---
10(00)
sin
nHz/d
+
e-
qdj2
shq(z
- d/2),
n
четное,
n
нечетное,
(В.27)
chq(z
- d/2)
XIF,2q(Z)
=
chqd/2
.
и
(В.26)
Хотя
эти
волноводные
моды
удовлетворяют
условию
X~q
=
о на
по
верхностях,
что
согласуется
с
экспериментами
по
КРС
в
обратном
направлении
[98]
для
мод
q =
О,
они
не
удовлетворяют
условиям
Xnq
=
О
при
z =
О
и
z = d.
В
отличие
от
мод
пластины
и
мод
Хуан
Куня-Жу,
волноводные
моды
имеют
ненулевые
экспоненциально
убывающие
значения
за
пределами
пластины:
Фnq(Z)
=
Фnq(О)
exp(qz)
при
z <
О
и
Фnq(Z)
=
Фnq(О)
exp[q(d - z)]
при
z>
d.
Окончательно
интерфейсные
моды,
удовлетворяющие
уравнению
\72
х
=
О,
даются
формулами
shq(z
- d/2)
XIF,lq(Z)
=
shqd/2

264
Приложения
Эти
выражения
согласуются
с
выражениями,
выведенными
в
гл.
7;
как
было
показано
там,
потенциалы
оптических
фононов
интерфейс
ных
мод
экспоненциально
убывают
с
расстоянием
от
пластины,
т.
е.,
как
exp(qz)
при
z <
О
и
exp[q(d- z)]
при
z>
d.
Представив
потенциал
взаимодействия
Фm(q,
z)
для
области
т
в
виде,
содержащем
квантовые
числа
n
и
q
этой
области,
запишем
гамильтониан
взаимодействия
для
каждого
полного
набора
нормиро
ванных
мод
в
следующем
виде:
н-;
=
-еФ(г)
=
-е
L
Фnq
e
iq
.
p
.
nq
(В.28)
Несомненно,
что
из
трех
обычно
используемых
наборов
фонон
ных
мод
только
моды
пластины
удовлетворяют
условиям
фф'
=
о при
z =
±оо
и
Xnq
=
X~q
=
о
при
z =
О
и
при
z = d.
Альтернативной
группе
граничных
условий
ФФ'
=
о при
z =
±оо
и
X~q
=
о при
z =
=
о и
при
z = d
не
удовлетворяет
ни один
из
обычно
используе
мых
наборов
фононных
мод.
Как
было
доказано
Нэшем
[96],
урав
нения
Эйлера-Лагранжа
(В.4)
и
(В.5)
удовлетворяются
в
каждом
слое
материала
и
обеспечивают
основу
для
определения
так
называе
мых
правил
сшивки
решений
на
каждой
поверхности
раздела.
В
без
дисперсионном
пределе
плотность
лагранжиана
не
содержит
членов
с
пространственными
производными
от
w,
а
потому
значимость
меха
нических
граничных
условий
в
этом
случае
неясна.
По
этой
причине
Нэш
исследовал
уравнения
Эйлера-Лагранжа
на
поверхностях
раздела
для
мод,
имеющих
ненулевую
дисперсию,
описываемых
плотностью
лагранжиана
(В.1).
Как
легко
видеть,
в
этом
случае
правила
сшивки
распространяются
на
величины
w j
у'р
и
Ф,
а
z-компонента
вектора
электрической
индукции,
D
z
=
(1j47Г)С:(ОО)Ф'
-
-
"(w
z
,
является
непрерывной
на
поверхностях
раздела.
Таким
образом,
в
дисперсной
континуальной
модели
нет
противоречия
между
тем,
что
механические
граничные
условия
накладываются
на
величины
w
и
w'
и
тем,
что
одновременно
накладываются
электромагнитные
граничные
условия
на
величины
Ф
и
D.
Разумеется,
для получения полной
группы
нормальных
мод
нужно
использовать
оба
типа
граничных
условий.
В
качестве
иллюстрации
значимости
вклада,
внесенного
Нэшем
в
понимание граничных
условий
для
имеющейся
системы,
полезно
специально
немного
упростить
текущий
анализ,
рассмотрев
уравнение
с:(оо)V'Ф
- 4n"(w =
О.
(В.29)
Выражение,
стоящее
слева,
возникает
в
уравнении
Эйлера-Лагранжа,
получающемся
путем
вариации
плотности
лагранжиана
по
Ф:
V' .
[с:(оо)V'Ф
- 4n"(w] =
О.
Понятно,
что
одного
этого
упрощенного
уравнения
недостаточно
для
полного
описания
системы,
но
это
то
самое
уравнение,
которое
используется
в
механических
моделях
для
получения
продольных
мод
и
построения
на
их
основе
нормальных
мод.

Приложенив
В
265
(В.30)
2ne
2
n
UJ
LO [ 1
1_]
V
Е(ОО)
Е(О)
Рассмотрим
уравнение
(В.29)
и
покажем,
что
оно
дает
тот
же
гамильтониан
фрёлиховского
взаимодействия
электрона
с
полярным
оптическим
фононом,
что
получен
в
§ 1
гл.
5.
Подставляя
величину
"(,
выраженную
через
-ъо.
Е(О)
и
Е(ОО),
сразу
получаем
выражение
\7ф
=
UJLQ
{41Г
[E(~)
-
E(~)]
}
1/2
w.
Затем,
используя
выражение
w = JJ-lN/V
и,
приведенное
в
прило
жении
А,
и
формулу
нормированного
смещения
(см.
§ 1
гл.
5)
для
случая,
когда
UJ
q
=
UJLO
и
только
продольная
поляризация
вносит
свой
вклад,
получаем
следующее
выражение:
{
[
1 1
]}
1/2
\7Ф=UJLQ
41Г
Е(ОО)
-
Е(О)
Х
Затем,
используя
соотношение
\7ф
=
-iqФ
и
умножая
Ф
на
-е
для
получения
гамильтониана,
получаем
" 1 .
t·
L.J - (a
q
е
Щ
·
Г
+ a
q
е-
Щ
·
Г
)
.
q q
(В.32)
что
в
точности
соответствует
результату,
полученному
в
§ 2
гл.
5.
Таким
образом,
упрощенное
уравнение
Е(оо)\7Ф
- 4n"(w =
О дает
правильный
трехмерный
гамильтониан
фрёлиховского
взаимодействия.
Однако
этот
успешный
результат
не
дает
оснований
использовать
урав
нение
Е(оо)\7Ф
- 4n"(w =
О
вместо
уравнения
\7.
[Е(оо)\7Ф
- 4n"(W] =
О
при анализе
граничных
условий
для
фононных
мод
В
пластине.
Дей
ствительно,
как
показано
Нэшем
[96],
продольные
волны,
полученные
из
этого
упрощенного
уравнения,
не
обеспечивают
достаточного
числа
свободных
пара
метров
для
одновременного
выполнения
механических
и
электромагнитных
граничных
условий.
Понимание
этих
явлений,
достигнутое
в
работе
Нэша
[96],
было
важным
фактором
для
нахождения
правильных
подходов
к
расчету
частоты
рассеяния
носителей
на
оптических
фононах
в
размерно-огра
ниченных
структурах.
Конечно
же,
ключевым
моментом
этого
расчета

266
Приложения
является
выбор
полного
ортогонального
набора
фононных
мод.
Несмот
ря на
то
что
только
моды
пластины
удовлетворяют
желаемым
гра
ничным
условиям,
Нэш
продемонстрировал
путем
вычислений
в
явном
виде,
что
любой
из
трех
наборов
полных
ортогональных
мод
-
моды
пластины
в
сочетании
с
интерфейсными
модами,
моды
Хуан
Куня
Жу
в
сочетании
с
интерфейсными
модами
и
волноводные
моды
-
может
использоваться
в
качестве
базиса
для
определения
частот
внут
риподзонного
и
межподзонного
рассеяния
электронов
на
фононах.
Нэш
показал,
что
для
квантовой
ямы,
имеющей
ширину
d,
справедливо
выражение
е
2
L 1
UIФnq
(z)1i)
12
сх
UJ~q
f d
2
q
21
n1
(q)ni (q)fn(q),
q q
где
форм-фактор
fn(q)
дается
формулой
fn(Q)
=
IfdZnо(Z),6Фnq(z)12
d *q
UJ~O
XnqXn'q'
UJ
nq
и
где
(В.33)
(В.34)
n1
(q)
= f d
2
pe-
iq
.
p
n1
(р),
n1
(Р)
=
фi(Р,
f)ф1
(р,
i),
no(z) =
фо(z, f)фо(z,
i).
(В.35)
Таким
образом,
для
данной
величины
импульса
Q
форм-фактор
fn(q)
описывает
вероятность
того,
что
электрон
будет
рассеян
из
подзоны
li)
в
подзону
IЛ
в
результате
взаимодействия
с
фононами
ветви
n.
Численные
вычисления,
проведенные
Нэшем
[96]
в
явном
виде,
пока
зали,
что
форм-факторы
fn(q),
соответствующие
трем
полным
наборам
ортогональных
мод:
модам
пластины
в
сочетании
с
интерфейсными
мо
дами,
модами
Хуан
Куня-Жу
с
интерфейсными
модами
и
волноводным
модам,
-
идентичны.
Это
результат
иллюстрируют
рис.
В.1
дЛЯ
слу
чая
внутриподзонных
переходов
и
рис.
В.2
дЛЯ
случая
межподзонных
переходов.
Эти
результаты
означают,
что
любой
из
трех
полных
наборов
орто
гональных мод
для
рассмотренного
выше
полупроводникового
слоя
мо
жет
быть
использован
для
расчета
рассеяния
электронов
на
колебаниях
почти
вырожденных
продольных
оптических
фононных
мод
в
этом
слое.
Ключевым
моментом
является
то,
что
каждый
из
трех
наборов
мод
должен
быть
полным
и
ортогональным.
Это
объясняет,
почему
для
выполнения
такого
расчета
могут
быть
использованы
относительно
простые
моды
так
называемой
пластинной
модели,
хотя
эти
моды
и
не
являются
нормальными
модами
гетероструктуры,
содержащей
указанный
слой.
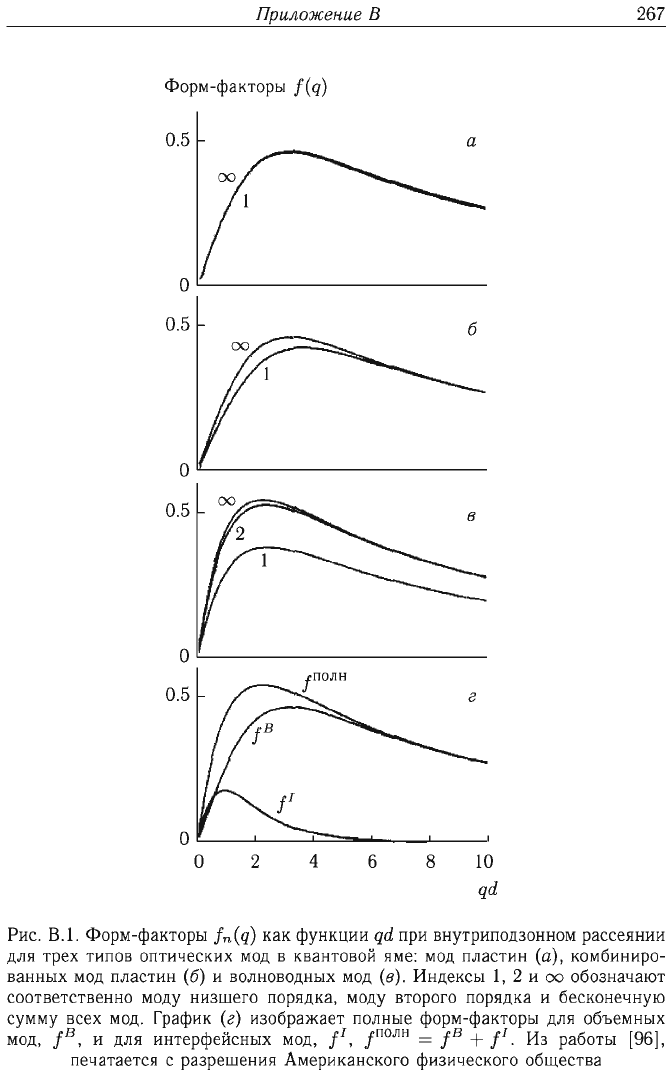
Приложенив
В
267
Форм-факторы
f(q)
0.5
а
10
qd
8
6
4
2
0'--------------
0.5
0"---------------
0.5
0"--------------
0.5
Рис.
8.1.
Форм-факторы
fn(q)
как
функции
qd
при
внутриподзонном
рассеянии
для
трех
типов
оптических
мод
в
квантовой
яме:
мод
пластин
(а),
комбиниро
ванных
мод
пластин
(6)
и
волноводных
мод
(в).
Индексы
1,2
и
00
обозначают
соответственно
моду
низшего
порядка,
моду
второго
порядка
и
бесконечную
сумму
всех
мод.
График
(г)
изображает
полные
форм-факторы
для
объемных
мод,
fB,
и
для
интерфейсных
мод,
fI,
fПОЛН
=
fB
+
fI.
Из
работы
[96],
печатается
с
разрешения
Американского
физического
общества
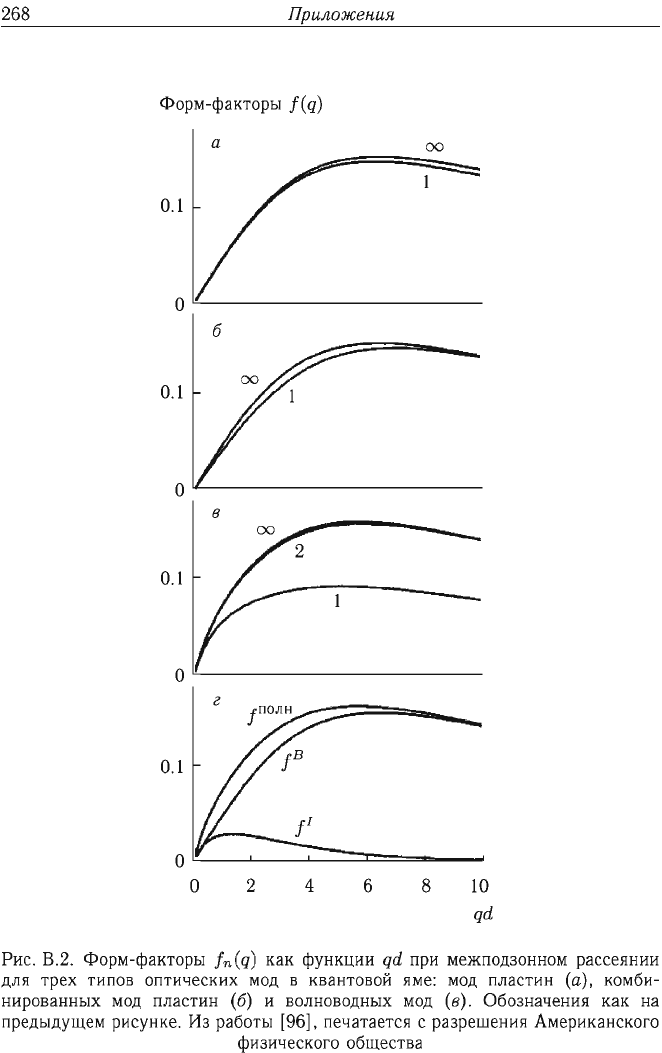
268
Приложения
Форм-факторы
f(q)
а
00
0.1
О
~------------
6
0.1
О
~------------
8
10
qd
86
42
0"---------------
0.1
0.1
Рис.
В.2.
Форм-факторы
fn(q)
как
функции
qd
при
межподзонном
рассеянии
для
трех
типов
оптических
мод
в
квантовой
яме:
мод
пластин
(а),
комби
нированных
мод
пластин
(6)
и
волноводных
мод
(8).
Обозначения
как
на
предыдущем
рисунке.
Из
работы
[96],
печатается
с
разрешения
Американского
физического
общества

Приложенив
В
269
в
качестве
дальнейшего
доказательства
применимости
этого
под
хода
Нэш
показал,
что
три
вышеперечисленных
набора
мод
-
на
бор
мод пластины
и
интерфейсных
мод,
набор
мод
Хуан
Куня-Жу
и
интерфейсных
мод
и
набор
вол но
водных
мод
-
связаны
унитарными
преобразованиями.
Его
доказательство
демонстрирует,
что
в
диэлек
трической
континуальной
модели
с
электромагнитными
граничными
условиями
важно
включить
в
полный
набор
мод,
наряду
с
мода
ми
пластин,
также
и
интерфейсные
моды
оптических
фононов.
Это
же
относится
и
к
модели
Хуан
Куня-Жу.
Существенно
также,
что
интерфейсные
моды
не
включены
в
набор
волноводных
мод:
этот
набор
мод
является
полным
и без них.
Действительно,
в
отличие
от
мод
пластины
и
мод
Хуан
Куня-Жу,
волноводные
моды
явно
включа
ют
в
себя
экспоненциально
затухающие
вне
пластины
компоненты,
сходные
с
интерфейсными
модами.
Диэлектрическая
континуальная
модель
с
электромагнитными
граничными
условиями
дает
набор
мод,
включающий
моды
пластины
и
интерфейсные
моды,
который
удобен
для
проведения
относительно
простых
расчетов
частоты
рассеяния
электронов
на
фононах
в
случае,
когда
необязательно
учитывать
дис
персию
размерно-ограниченных
мод.
Этот
случай
иногда
называют
слу
чаем
квази-объемных
мод
в
пластине.
Для
арсен
ида
галлия
и
арсенида
алюминия
общая
величина
дисперсии
в
пределах
зоны
Бриллюэна
составляет
всего
несколько
мэВ,
так что
в
типичных
расчетах
переноса
носителей,
включая
и
расчеты
твердотельных
электронных
приборов
с
размерно-ограниченными
структурами,
эту
дисперсию
учитывать
необязательно.
Как
пока
за
но
в
гл.
10,
даже
разницу
энергий
в
несколь
ко
мэВ,
необходимо
учитывать
при
моделировании
оптоэлектронных
приборов,
таких
как
полупроводниковые
лазеры
с
квантовыми
ямами.
В
заключение
этого
приложения
чрезвычайно
поучительно
про
вести
графическое
сравнение
различных
макроскопических
и
микро
скопических
мод
оптических
фононов
в
двумерных
гетероструктурах.
В
работах
[106]
проведены
прямые
сравнения
мод
пластины,
волноводных
мод
и
мод
Хуан
Куня-Жу
с
модами,
вычисленными
с
помощью
микроскопической
модели,
основанной
на
основополагаю
щих
принципах
(аЬ
initio).
На
рис.
В.З
представлены
распределения
z-компоненты
U
z
смещения
атомов
и
соответствующего
потенциала
V
для
каждой
из
этих
мод,
описанные
в
работах
[106].
Оптические
моды
представлены
для
квантовой
ямы
в
арсениде
галлия,
имеющей
ширину
56
'А
и
ориентацию
(001)
и
окруженной
двумя
слоями
арсенида
алюминия.
Границы
раздела
обозначены
вертикальными
черточками,
и
приняты
следующие
величины
волновых
векторов
фононов:
qz =
О
и
qll
=
О,
15
'А
-1.
На
рис.
В.4
представлено
подробное
сравнение
распределения
электрического
потенциала
интерфейсных
мод,
рассчитанных
через
макроскопические
и
через
микроскопические
модели.
Как
и
следовало
ожидать,
наблюдается
хорошее
согласие
между
макроскопическими
и
микроскопическими
расчетами
[106].
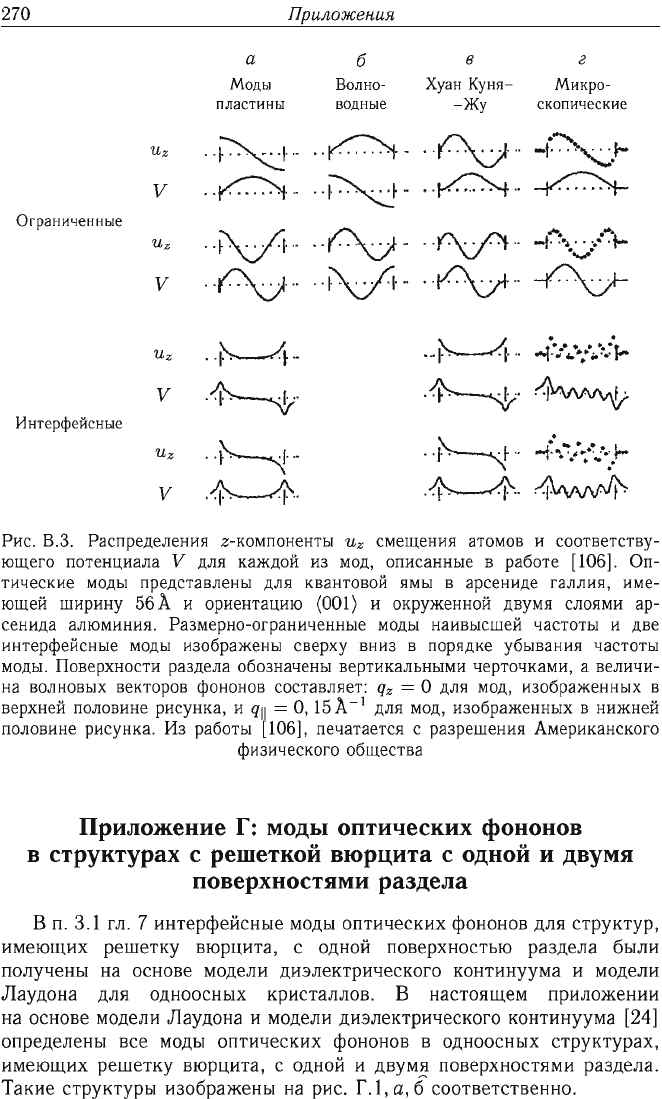
270
а
Моды
пластины
Приложения
б
Волно
водные
в
Хуан
Куня
-Жу
г
Микро
скопические
Ограниченные
U
z
v
U
z
v
..
~
~.
-Г\.)
...
"(~v..:.:..l'-
..
~
~_
..
~
..
~
..
~
AJ--
..
~
..
-t~~
.••
~/':.t-
··Аи···
..
~.-
..
~
..
~
Интерфейсные
v
v
..
f'--4
..
.~.
..
~
...
.ф.-4.
\. / . .
•..j.-----......:j...
...J:,t
""
......
Xf.--
.~.~
.
'I~"I-"
-{
..
~:
••
~ ~
•.
!-
I··~
......
.
ф.-4.~
Рис.
В.З.
Распределения
в-компоненты
и.;
смещения
атомов
и
соответству
ющего
потенциала
V
для
каждой
из
мод,
описанные
в
работе
[106].
Оп
тические
моды
представлены
для
квантовой
ямы
в
арсениде
галлия,
име
ющей
ширину
5611.
и
ориентацию
(001)
и
окруженной двумя
слоями
ар
сенида
алюминия.
Размерно-ограниченные
моды
наивысшей
частоты
и
две
интерфейсные
моды
изображены
сверху
вниз
в
порядке
убывания
частоты
моды.
Поверхности
раздела
обозначены
вертикальными
черточками,
а
величи
на
волновых
векторов
фононов
составляет:
qz =
о
для
мод,
изображенных
в
верхней
половине
рисунка,
и
qll
=
О,
15
11.-1
для
мод,
изображенных
в
нижней
половине
рисунка.
Из
работы
[106],
печатается
с
разрешения
Американского
физического
общества
Приложение
Г:
моды
оптических
фононов
в
структурах
с
решеткой
вюрцита
с
одной
и
двумя
поверхностями
раздела
в
п.
3.1
гл.
7
интерфейсные
моды
оптических
фононов
для
структур,
имеющих
решетку
вюрцита,
с
одной
поверхностью
раздела
были
получены
на
основе
модели
диэлектрического
континуума
и
модели
Лаудона
для
одноосных
кристаллов.
В
настоящем
приложении
на
основе
модели
Лаудона
и
модели
диэлектрического
континуума
[24]
определены
все
моды
оптических
фононов
в
одноосных
структурах,
имеющих
решетку
вюрцита,
с
одной
и
двумя
поверхностями
раздела.
Такие
структуры
изображены
на
рис.
Г.l,
а,
g
соответственно.
