Строшио М., Дутта М. Фононы в наноструктурах
Подождите немного. Документ загружается.


§ 1.
Фрёлиховекий
потенциал
для
продольных
фононое
161
в
соответствии
с
этим,
частота
переходов
s{e,a}(k,
k')
дается
выра
жением
s{e,a}(k,k') =
1~~22
Ik
_1
k'1
2
(n
q
+
'/2
±
'/2)
8(E(k') - E(k) ± hw) =
=
IC
l2
2
i-
(n
q
+
'/2
±
'/2)
8(E(k') - E(k) ± hw), (8.10)
41Гп'
q
где
q2 =
Iq12,
а
дельта-функция
выражает
сохранение
энергии
E(k') - E(k) =
~hw,
причем
верхний
знак отвечает
испусканию
фонона,
а
нижний
-
поглощению
фонона.
Зависимость
вида
Iql-2
в
выражении
для
s{e,a}(k,
k')
имеет
тот
же
вид,
что
и
зависимость,
появляющаяся
при
учете
кулоновского
взаимодействия.
Соответствен
но,
можно
ожидать,
что
конечное
значение
частоты
рассеяния
может
быть
получено
только
в
том
случае,
если
правильно
учтены
эффекты
экранирования.
Поэтому
выражение
для
s{e,a}(k,
k')
переписывается
в
виде
где
qo
-
параметр
отсечки,
введенный
для
учета
экранирования
при
кулоноподобном
взаимодействии.
Окончательное
значение
частоты
рас
сеяния
будет
вычислено
путем
перехода
к
пределу
qo
----+
О.
Полная
частота
рассеяния
для
всего
объема
l/тз\;,а}
(k),
связанная
с
величиной
si~a}
(k,
k'),
получается
путем
интегрирования
последней
по
q
и
умножением
на
объем
образца
V:
1
ICI
2V
-----,-------,,------
-
--
(n +
'/
±
'/
)
х
тз\;,а}(k)
-
41Гп
2
q 2 2
27r
тг
Х
f
d<p
fdBsinB fd
qq2
(q21
2
q
g)2
8(E(k') - E(k) ± hw). (8.12)
о о
Интегрирование
по
<р
дает
коэффициент
21Г,
поскольку
в
рассматри
ваемой
задаче
зависимость
от
<р
отсутствует.
При
выполнении
инте
грирования
по
В
необходимо
учитывать
тот
факт,
что
аргумент
дельта
функции
зависит
от
В.
Если
считать
зоны
носителей
параболическими,
то,
обозначив
через
k
начальный
волновой
вектор
носителя,
а
массу
носителя
-
через
т,
можем
переписать
аргумент
дельта-функции
следующим
образом:
6
М.
А.
Сторшио,
М.
Дутта

162
Гл.
8.
Рассеяние
носителей
на
продольных
оnтич.еских
фононах
E(k')
-
E(k)
±
Тио
=
E(k
=f q) -
E(k)
±
Тио
=
n
2
(k
=f q)2 _
(n
2
(k )2
±
Ти»
=
~
[(k')2 _
(k)2J
±
Ти»
=
2т 2т 2т
n
2
=
2т
(q2
=f
2qk
c
o sВ)
±
Ти».
(8.13)
Интеграл
по
В
теперь
берется
с
использованием
соотношения
f
g(
В)
I
g(B)
б[f(В)
-
a]dB
= df/dB 0=00 '
где
Во
определяется
из
равенства
f(B
o
) =
а.
Теперь,
положив
n
2
f(B) = =f
2m
(2qkcosB)
и
обозначив
и
= cos
В,
находим
значение
интеграла:
27Г
( 2 )
I
dВsiпВб
:т
(q2
=f
2qk
c
o
sВ)
±
ь:
=
f
l
(n
2
n
2
)
m
=
duб
2т
(=f
2
qku)
+
2т
q2
±
Ти»
= =fn
2
qk '
-1
так
что
(8.14)
(8.15)
(8.16)
(8.17)
Мы
рассматриваем
диапазоны
q,
связанные
с
испусканием
и
поглоще-
{
{
е
}
{е}}
{{а}
{а}}
Д
u
нием,
qmin'
qmax
И
qmin'
qmax
соответственно.
иапазон
значении
q
определяется
из
уравнения
2 2mw
q -
2qk
c
o
sВ
±
-n-
=
о,
(8.18)
где
верхний
знак
соответствует
испусканию,
а
нижний
-
поглощению.
Корнями
этого
уравнения
являются
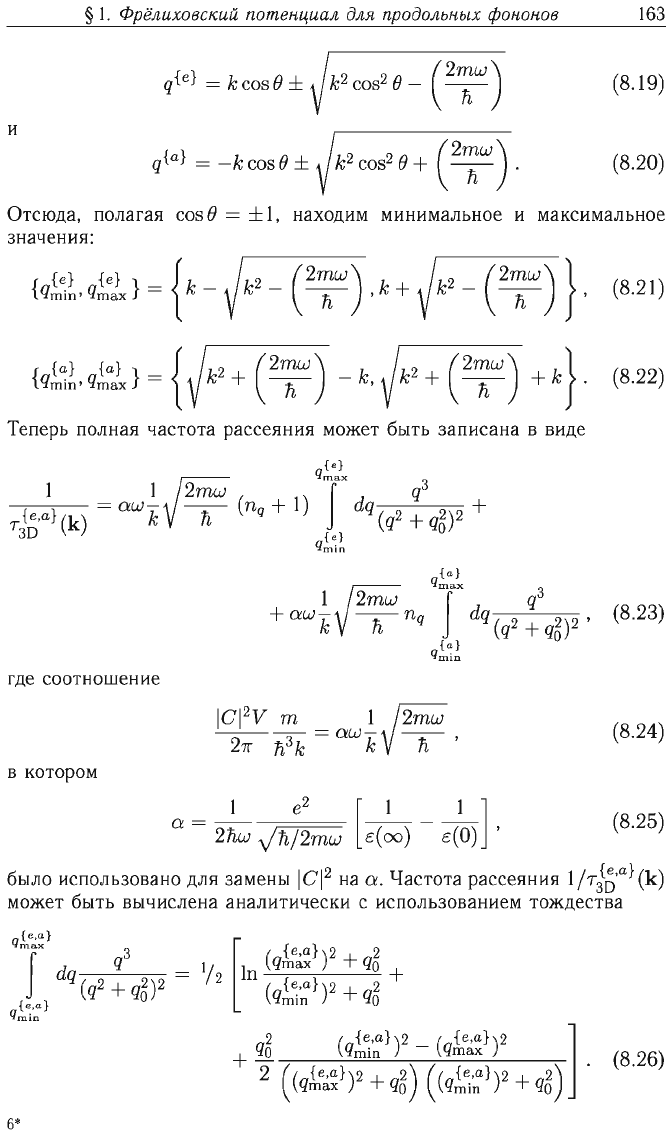
§ 1.
Фрёлиховекий
потенциал
для
продольных
фононое
163
и
q{e}
= kcos(} ±
k
2
2 ()
(2mw)
cos -
--
н
(8.19)
(8.20)
q{a}
=
-kcos(}±
k
2cos
2
(}
+
(2~W).
Отсюда,
полагая
cos
()
= ± 1,
находим
минимальное
и
максимальное
значения:
{
{
а
}
{а}}
_ {
qmin'
qmax
-
{
{~}
{е}}
=
{k
_
Vk2
-
(2mw)
k V
k2
_
(2mw)
}
qmш,qmах
n
,+
n'
k
2
+
C~~)
Н}
Теперь
полная
частота
рассеяния
может
быть
записана
в
виде
(8.21 )
(8.22)
где
соотношение
в
котором
(8.24)
а
=
2~и;
Jn;~mw
[€(
~)
-
€(~)]
, (8.25)
было
использовано
для
замены
ICl
2
на
а.
Частота
рассеяния
1
jтз);,а}
(k)
может
быть
вычислена
аналитически
с
использованием
тождества
(8.26)
5*

164
Гл.
8.
Рассеяние
носителей
на
продольных
оnтич.еских
фононах
Пренебрегая
членами
порядка
О(qб),
получаем
1 _
aw'-J2mы
(k+ y'k' -
2mw/h
)'
+
qб
{е,а}
- 2 k
1t
(n
q
+ 1)
lп
2 +
Т
З
D
(k)
(k
-
Jk2
- 2mUJ/1t) +
qб
а,"
1
J2mы
(y'k' +
2mы/h
+k)' +
qб
+
2k
-п-
nq
1п
2 . (8.27)
(
Jk2
-
2mUJ
/п
-
k)
+
qб
в
пределе
qo
----+
О
получаем
окончательное
значение
частоты
рассея
ния:
1 _
O:UJ
1J2mUJ ( 1)1 k +
Jk2
-
2mUJ/1t
-----,-------,---
-
--
--
n + n +
тз{~,а}(k)
2 k
1t
q k -
Jk2
-
2mUJ/1t
+
O:UJ
~J2mUJ
»«
1п
Jk
2
+
2mUJ/1t
+
k.
(8.28)
2 k
1t
Jk2
-
2mUJ/1t
- k
1.2.
Частоты
рассеяния
в
объемных
полупроводниках
с
решет
кой
вюрцита.
Фрёлиховский
гамильтониан
взаимодействия,
приве
денный
в
§ 1
гл.
7
для
полярного
одноосного
кристалла
(UA),
может
быть
записан
в
виде
H:?r
A
= 2)
-е)ф(q)
eiq,r(a
q
+
a~q)
q
UA _
."
J2~е'Т,
1
ое"(
t)(
2 2)( 2
2)
H
Fr
-
26
VUJ
q
е
a
q
+ a_q
UJTO,l..
-
UJ
q
UJTO,II
-
UJ
q
Х
q q
(8.29)
где

(8.33)
§ 1.
Фрёлиховекий
потенциал
для
продольных
фононое
165
а
О
-
угол
между
волновым
вектором
фонона
q
и
осью
С.
Также
из
уравнения
(3.21)
следует
равенство
6"1..(ш)siп
2О+6"II(ш)соs
20=О.
(8.32)
Как
обсуждалось
в
§ 2
гл.
3,
высокочастотный
электронный
отклик
среды
не
должен
существенно
зависеть
от
кристаллической
структуры,
и
обычно
допускается
[18],
что
6"1..(00)
~
6"11(00).
Тогда
ш
2
ш
2
ш
2
-
ш
2
LO.1..
- . 2
О
+
LЩI
2
О
-
О
2
2
S
Ш
2
2COS-,
Што,1..
-
ш
ШТО,II
-
ш
или,
в
эквивалентном
виде:
4
(2
2) 2 2 2 2
О
2 2 . 2
О
О
со
-
ШI
+
Ш2
ш
+
Што,1..
ШLЩI
COS +
ШLО,1..
ШТО,II
SШ
= ,
где
(8.34)
2 2
.20
2 20
ШI
=
ШТО,II
sш
+
Што,1..
COS ,
2 2 .
20 2 20
Ш2
=
ШLЩI
sш
+
ШLО,1..
COS .
(8.35)
В
§ 2
гл.
3
было
показано,
что,
когда
Iшто,1..
-
ШТО,III
«
ШLQ,II
-
ШТО,II
и
Iшто,1..
-
ШТЩII
«
-ъо.;
-
-то.г.
это
уравнение
имеет
следующие
корни:
где
(ш
2
ш
2
)(ш
2
ш
2)
л
2(0) _ 2
LЩI-
LO,1..
тщl-
то,1..
. 20 20
Uш
- 2 2
SШ
COS .
Ш2
-ШI
Таким
образом,
один
корень
имеет
вид
п2
2 2 . 2
О
2 2
О
Нто
=
ш
=
што,
11
sш
+
-то.;
COS -
(шlО,11
-
шIо,1..)
(ш?о,
11
-
Ш?о,1..)
. 2
О
2
О
-
22
SШСОS
~
Ш2
-ШI
~
2
.20
2 20
~
ШТО,II
sш
+
-то.;
COS ,
а
другой:
п2
2 2 2
О
2 . 2
О
HLO =
ш
=
ШLО,II
cos +
ШLО,1..
SШ
+
(ш
2
-
ш
2
)
(ш
2
-
ш
2
)
+
LЩI
LO,1..
тщl
то,1...
20 20 ~
22
SШСОS
~
Ш2
-ШI
~
2 20 2
.20
~
ШLО,II
cos +
ШLО,1..
SШ
.
((8.36)
(8.37)
(8.38)
(8.39)

166
Гл.
8.
Рассеяние
носителей
на
продольных
оnтич.еских
фононах
Неравенства,
использованные
для вывода
выражений
для
п}о
и
ПIо'
удовлетворяются
как
для
нитрида
галлия
(GaN),
так
и
для
нитрида
алюминия
(AIN),
что
можно
проверить,
используя
численные
значения
частотных
параметров
этих
веществ,
приведенные
в
§ 3
гл.
3.
Угловая
зависимость
фононных
частот
ИК-активных
фононов
в
нитриде
галлия
показана
на
рис.
8.1,
где
е
-
угол
между
волновым
вектором
фонона
q
и
осью
с.
LО-типа
700
600
ТО
500
О
45
ТО-типа
90
Угол
е
(град.)
Рис.
8.1.
Угловая
зависимость
фононных
частот
со
ИК-активных
LO-
и
ТО
фононов
В
GaN.
е
-
угол
между
волновым
вектором
фонона
q
и
осью
с.
Из
работы
[92],
напечатано
с
разрешения
Американского
физического
общества
Как
было
показано
в
п.
1.1
гл.
8,
частота
рассеяния
электронов
на
оптических
фононах
может
быть
получена
путем
вычисления
с
использованием
золотого
правила
Ферми
частоты
переходов
для
гамильтониана
возмущения
Hi!/.
В
соответствии
с
этим
правилом
частота
B&~a}
(k,
k')
переходов
в
единице
объема
из
начального
состояния,
обозначаемого
Ik,
N
q
+
'/2
±
'/2;
и
соответствующего
состоянию
Ik;
электрона
и
состоянию
IN
+
'/2
±
'/2;
фонона,
в
конечное
состояние,
обозначаемое
(k',
н,
+
?/2
±
'/21
и
соответству
ющее
состоянию
(k'l
электрона
и
состоянию
(N
q
+
'/2
±
'/21
фонона,
дается
выражением
где
S&~a}(k,k')
=
2:
L
IMiт~a}(q)12
б(Е(k')
- E(k) ±
nUJ),
q
(8.40)
(8.41)

§ 1.
Фрёлиховекий
потенциал
для
продольных
фононое
167
Как
показано
в
п.
1.1
гл.
8,
состояния
электрона
имеют
вид
плоских
волн,
нормированных
на
объем
V:
Ik) = e
i
k.
r
/VV
и
Ik') =
e-ik'.r
/vv.
(8.42)
ДЛЯ
UJ2
=
sЧо
матричный
элемент
IМд~а},ТО(q)12
дается
выраже
нием
[92]
I
M{e,a},TO(q)1
2
=
27Ге
2
п,
х
UA
Vq2r2TO
(
2
2)2
. 2
()
2
()
Х
UJTO,..l
-
UJTO,II
sш
cos
х
[E..l
(О)
-
E..l
(00)
]2UJio,..l
cos
2
()
+
[EII
(О)
-
EII
(00
)]2UJio,11
sin
2
()
Х
(n
q
+
'/2
±
'/2),
(8.4З)
Этот
матричный
элемент
в
общем
случае
не
обращается
в
нуль,
так
как
в
одноосном
кристалле
мода
ТО-типа
на
самом
деле
не
является
чистой
ТО-модой.
В
случае
же
изотропного
материала
-то.л
=
UJTO,II'
а
мат-
ричный
элемент
для
поперечных
волн
стремится
к
нулю.
Аналогичным
образом
при
UJ2
=
r2Lo
матричный
элемент
IМд~а},LО(q)12
определяется
выражением
I
M{e,a},LO(q)1
2
=
27Ге
2
п,
Х
UA
Vq2r2LO
х
[sin
2
()
cos
2
()
]-'
Х
[1/E..l(00)
-
1/E..l(0)]UJ[O,..l
+
[1/EII(00)
-
1/EII(0)]UJ[O,11
Х
(n
q
+
'/2
±
'/2).
(8.44)
В
изотропном
пределе
-т.о.;
=
UJLO,II'
а
матричный
элемент
для
про
дольных
волн
принимает
вид
LO-
и
IМд~а},LО(q)12
=
2ne~~~LO
[1/E..l(00)
- 1/E..l(0)]
(n
q
+ '/2 ±
'/2)'
(8.45)
IMql
Численно
рассчитанные
значения
матричного
элемента
1
м82
(q)
12,
соответствующего
поглощению
фононов
ТО-типа
в
объемном
образце
GaN,
приведены
на
рис.
8.2.
Частоты
рассеяния
фононов
LO-
и
ТО-типа
были
числен
но
рассчитаны
в
работе
[92]
для
двух
задач:
как
функции
угла
()k
направления
распространения
электрона
относи
тельно
оси
С
при начальной
энергии
электрона
О,З
эВ

168
Гл.
8.
Рассеяние
носителей
на
продольных
оптических
фононах
IMql
(произв.
един.)
1
LО-типа
0.5
ТО-типа
о
45
90
Угол
е
(град.)
Рис.
8.2.
Величина
матричного
элемента
IMql
поглощения
оптических
фононов
как
функция
е
для
кристалла
GaN;
е
-
угол
между
волновым
вектором
фонона
q
и
осью
с.
Из
работы
[92],
напечатано
с
разрешения
Американского
физического
общества
и
как
функции
энергии
электрона
для
Bk
=
О
и
Bk
=
7г
/2.
Эти
результаты
отображены
на
рис.
8.3,8.4.
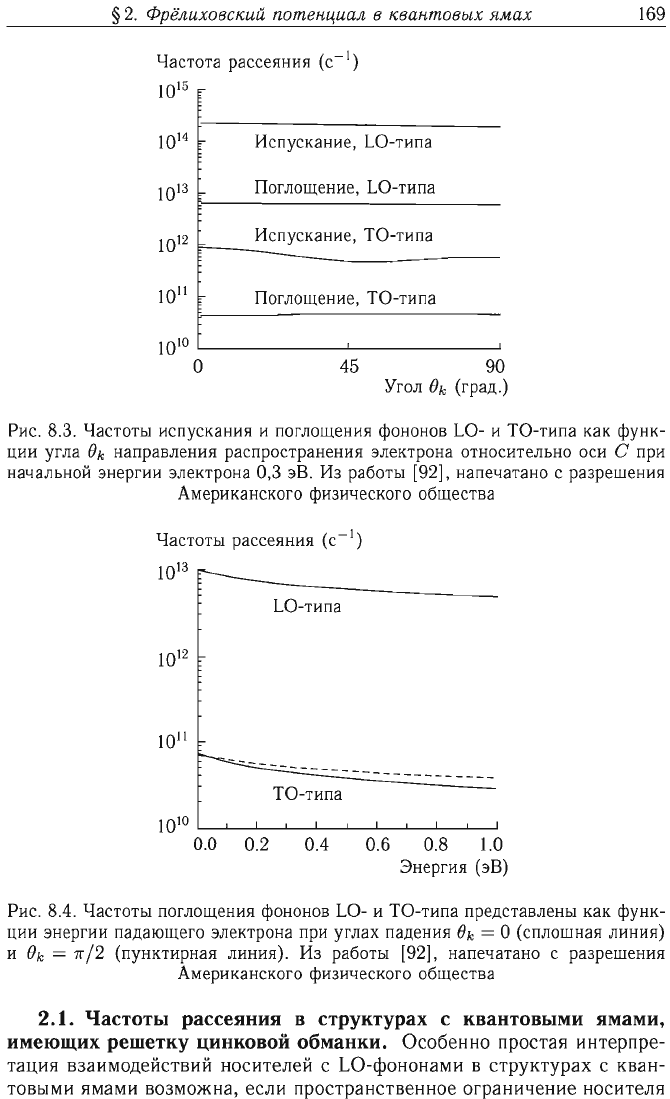
На
рис.
8.3
частоты
испускания
и
поглощения
фононов
LO-
и
ТО-типа
представлены
как
функции
угла
Bk
направления
распространения
электрона
относительно
оси
С
при
начальной
энергии
электрона
0,3
эВ.
На
рис.
8.4
значения
частоты
поглощения
фононов
LO-
и
ТО-типа
представлены
в
некотором
диапазоне
энергий
электрона
для
углов
Bk
=
О
И
Bk
=
7г
/2.
§ 2.
Фрёлиховский
потенциал
в
квантовых
ямах
Гамильтониан
фрёлиховского
взаимодействия,
приведенный
в
урав
нении
(5.34),
описывает
взаимодействие
носителей
с
полярными
опти
ческими
фононами
в
объемной
среде.
Как
отмечалось
в
п.
3.2
гл.
7,
фрёлиховский
гамильтониан
для
двумерной пластины
имеет
вид
(7.71).
А
гамильтониан
фрёлиховского
взаимодействия
для
интерфейсных
оптических
фононных
мод
в
диэлектрической
пластине
дается
выраже
нием
(7.72).
Гамильтонианы
взаимодействия,
приведенные
в
п.
3.1
гл.
7,
описывают
фрёлиховский
потенциал
для
случая
двумерной
пластины,
граничащей
со
средой,
в
которой
s = 1 [88].
В
настоящем
параграфе
гамильтонианы,
описывающие
взаимодей
ствия
носителей
с
полярными
оптическими
фононами,
будут
исполь
зоваться
для
вычисления
частот
рассеяния носителей
на
LО-фононах
с
использованием
золотого
правила
Ферми.
§2.
Фрёлиховекий
потенциал
в
квантовых
ям-ах
169
Частота
рассеяния
(с
-1
)
1015
1014
Испускание,
LО-типа
1013
Поглощение,
LО-типа
1012
Испускание,
ТО-типа
1011
Поглощение,
ТО-типа
45 90
Угол
()k
(град.)
1010
'--------"'----------'
о
Рис.
8.3.
Частоты
испускания
и
поглощения
фононов
LO-
и
ТО-типа
как
функ
ции
угла
()k
направления
распространения
электрона
относительно
оси
С
при
начальной
энергии
электрона
0,3
эВ.
Из
работы
[92],
напечатано
с
разрешения
Американского
физического
общества
Частоты
рассеяния
(с
-1
)
1013
LО-типа
ТО-типа
0.6 0.8 1.0
Энергия
(эВ)
0.4
1010
L--...1..----l..._'----'-----'-_"'----'------'-_..l...-.-'
0.0 0.2
Рис.
8.4.
Частоты
поглощения
фононов
LO-
и
ТО-типа
представлены
как
функ
ции
энергии
падающего
электрона
при
углах
падения
()k =
О
(сплошная
линия)
и
()k =
7г
/2
(пунктирная
линия).
Из
работы
[92],
напечатано
с
разрешения
Американского
физического
общества
2. t.
Частоты
рассеяния
в
структурах
с
квантовыми
ямами,
имеющих
решетку
цинковой
обманки.
Особенно
простая
интерпре
тация
взаимодействий
носителей
с
LО-фононами
в
структурах
с
кван
товыми
ямами
возможна,
если
пространственное
ограничение
носителя

170
Гл.
8.
Рассеяние
носителей
на
продольных
оnтич.еских
фононах
рассматривается
в
пределе
бесконечно
высокого
ограничивающего
по
тенциала
для
электронов,
известном
как
крайний
квантовый
предел,
а
фононы
рассматриваются
как
объемные.
В
этом
случае
в
процедуре
вычислений,
описанной
в
п.
1.1
гл.
8,
должно
быть
учтено
простран
ственное
ограничение
носителей
заряда.
Как
показано
в
п.
1.1
гл.
8,
частота
рассеяния
электронов
на
LО-фононах
может
быть
оценена
пу
тем
вычисления
на
основе
золотого
правила
Ферми
частоты
переходов
для
гамильтониана
возмущения
H
Fr
,
приведенного
в
§ 2
гл.
5.
Однако
в
данном
случае
состояния носителя
являются
состояниями
бесконечно
глубокой
квантовой
ямы.
В
соответствии
с
золотым
правилом
Ферми
частота
si~a}
(k,k')
переходов
на
единицу
площади
гетероструктуры
из
начального
состояния,
обозначаемого
Ik
2D
,N
q
+ '/2 ± '/2)
и
со
ответствующего
состоянию
Ik
2
D)
электрона
и
состоянию
IN
q
+
'/2
±
±
'/2)
фонона,
в
конечное
состояние,
обозначаемое
(k;D'
N
q
+
'/2
±
±
'/21
и
соответствующее
состоянию
(k;D
1
электрона
и
состоянию
(N
q
+
'/2
±
'/21
фонона,
дается
выражением
Si~a}(k,k')
=
2:
2:
IMi~,a}(q)12
д(Е(k')
- E(k) ±
hw),
(8.46)
q
где
в
этих
выражениях
знаки
плюс
и
минус
выбираются
так,
чтобы
отличать
начальное
и
конечное состояния
фонона.
В
случае
испус
кания
фонона
конечное
фононное
состояние
содержит
на
один
фо
нон
больше,
чем
начальное;
соответственно,
начальное
и
конечное
состояния
выбираются
в
следующем
виде:
Ik
2
D,
N
q
)
и
(k;D'
N
q
+
'/2
±
±
'/21.
Для
процессов
поглощения
фонона
начальные
и
конечные
со
стояния
выбираются
аналогичным
способом.
В
аргументе
дельта-функ
ции,
входящей
в
выражение
для
s{e,a}(k,
k')
и
описывающей
закон
сохранения
энергии,
верхний
знак
соответствует
испусканию
фонона,
а
нижний
-
поглощению.
Поскольку,
как
указано
в
п.
1.1
гл.
8,
состо
яния
электрона
и
фонона
относятся
к
разным
пространствам,
то
мож
но
записать:
Ik
2D
) IN
q
)
==
Ik
2D
,N
q
) .
Состояния
фононов
описываются
так
же,
как
в
§ 1
гл.
5,
а
фрёлиховский
гамильтониан
описывается
уравнением
(5.34)
2:
С
.
t·
Н
= -
(а
еЩ'Г
-
а
e-
tq
.
r
)
~
q q ,
q q
(8.48)
где
с=
-i
(8.49)
