Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления

Подождите немного. Документ загружается.

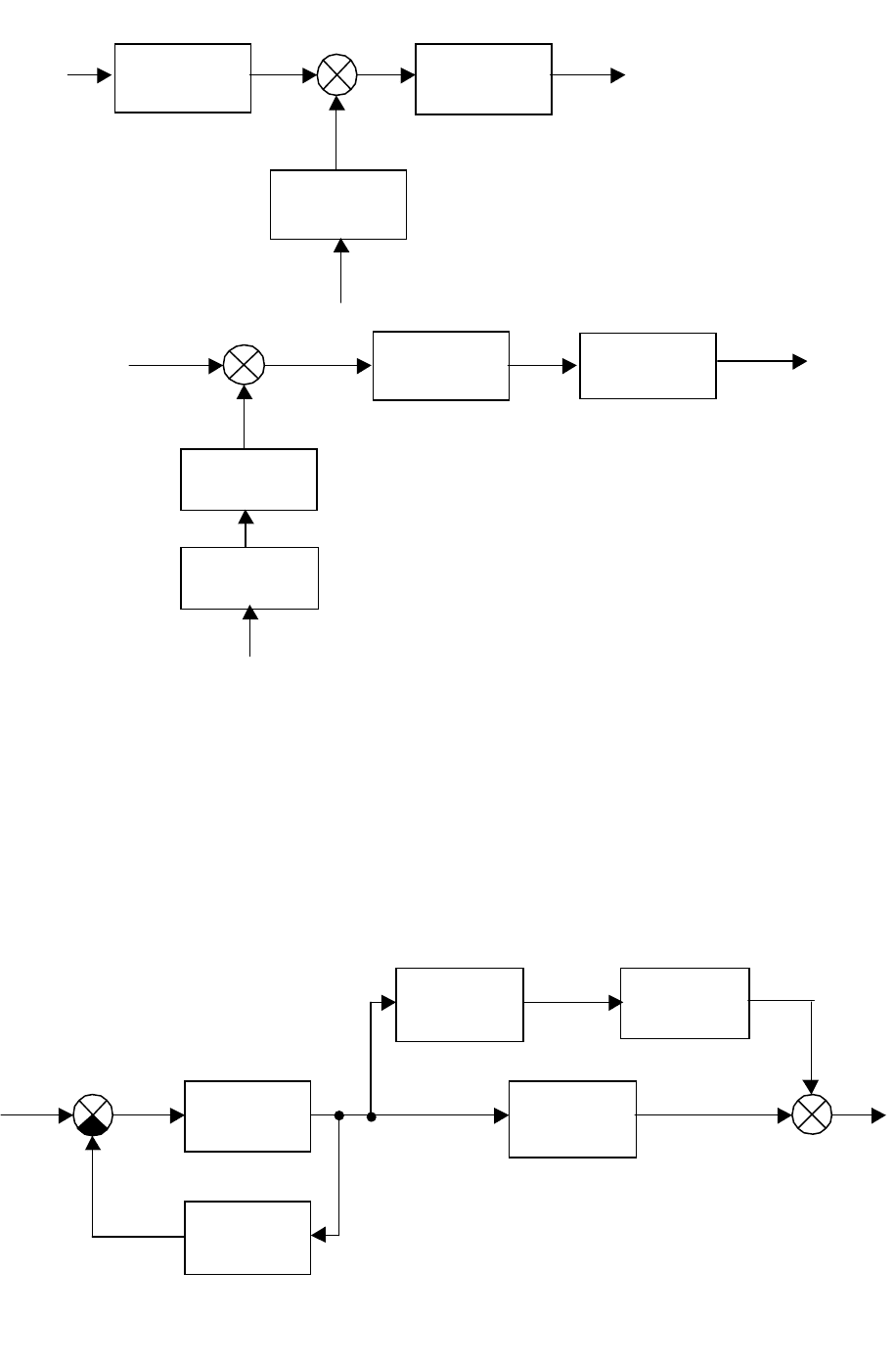
Рис. 2.34. Перенос звена

через сумматор

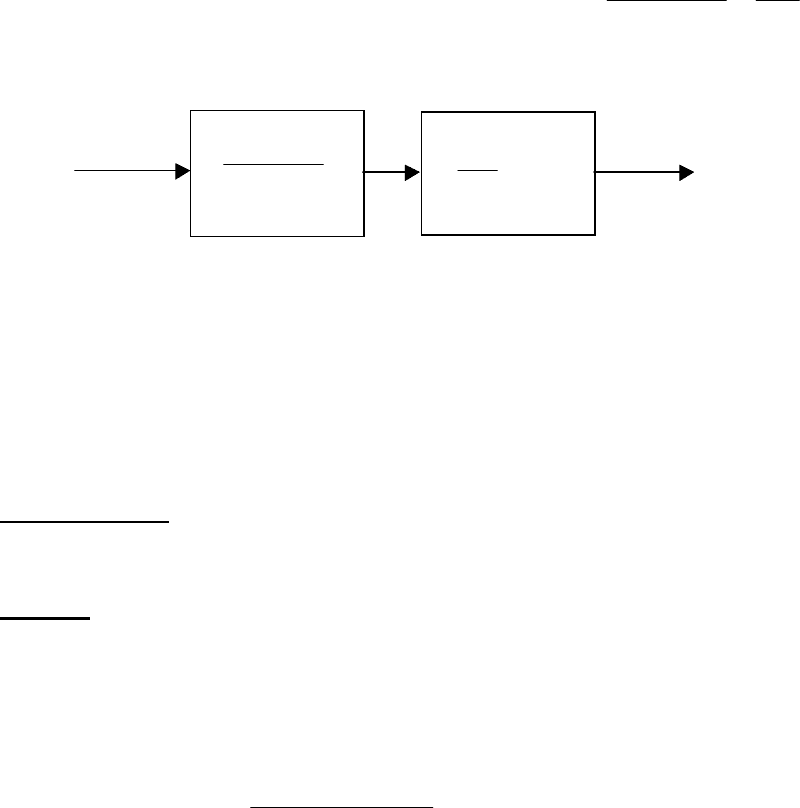
В качестве примера проведём упрощение структурной схемы, при-

ведённой на рис. 2.30. Перенесём динамическое звено с передаточной

функцией

W через точку разветвления

p . После этого получим схему,

состоящую только из элементарных соединений (рис. 2.35.).

Рис. 2.35. Схема соединения после переноса

1/ W

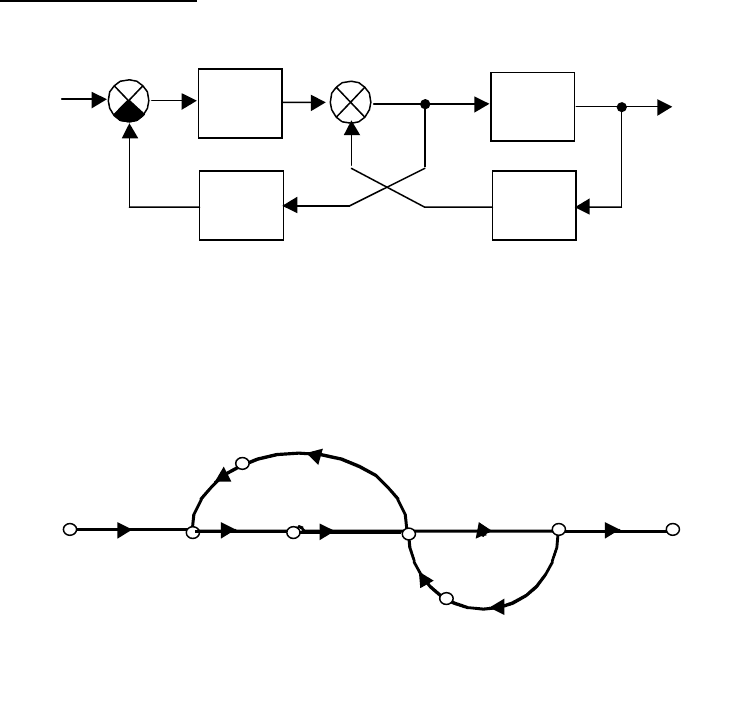
Теперь исходная система может быть представлена в упрощенном виде

(рис 2.36.) и будет описываться выражением:

⎟

⎠

⎞

⎜

⎝

⎛

+⋅

1 WW

Рис. 2.36. Исходная схема в упрощенном виде

2.8.2.3. Формула Мейсона

В случае громоздких систем с большим числом звеньев и перекре-

стных связей наиболее эффективным является использование для по-

лучения эквивалентных передаточных функций правила Мейсона. В

связи с этим введем необходимые дополнительные определения.

Прямой путь

между двумя заданными вершинами графа – это не-

прерывная последовательность ветвей одного направления, в которой

каждая из вершин встречается не более одного раза.

Контур

– замкнутая цепь, при однократном обходе которой в на-

правлении, указанном стрелками, каждая из вершин встречается не бо-

лее одного раза.

Согласно правилу Мейсона, передаточная функция

W между входом в

точке

и выходом в точке B равна:

∑

⋅

)(

)()(

)(

ppW

, (2.8-13)

где:

– число прямых путей между вершинами

и B ;

)(pW

– передаточная функция k-го прямого пути от вершины

к вер-

шине

B (она равна произведению передаточных функций всех ре-

бер, входящих в последовательность прямого пути);

)(

Δ – определитель графа;

)(p

Δ – k-й минор определителя графа, равный определителю более

простого графа, который получается из данного графа путем уда-

ления из него всех ребер и вершин, лежащих на k-м прямом пути, а

также всех ребер входящих и исходящих из этих вершин.

Определитель графа определяется из соотношения:

−

+−=Δ

∑∑

ojoi

pWpWpWp

)()()(1)(

−

∑

kji

okojoi

pWpWpW

)()()( , (2.8-14)

где

)(pW

– передаточные функции различных контуров графа;

)()( pWpW

ojoi

– произведения передаточных функций непересекающих-

ся пар контуров;

)()()( pWpWpW

ozojoi

– произведения передаточных функций непересек-

ающихся троек контуров.

ПРИМЕР 2.8-1

. Найти передаточную функцию

W для системы,

структурная схема которой приведена на рис. 2.37.

Рис. 2.37. Структурная схема системы с

пе

ек

ёстными связями

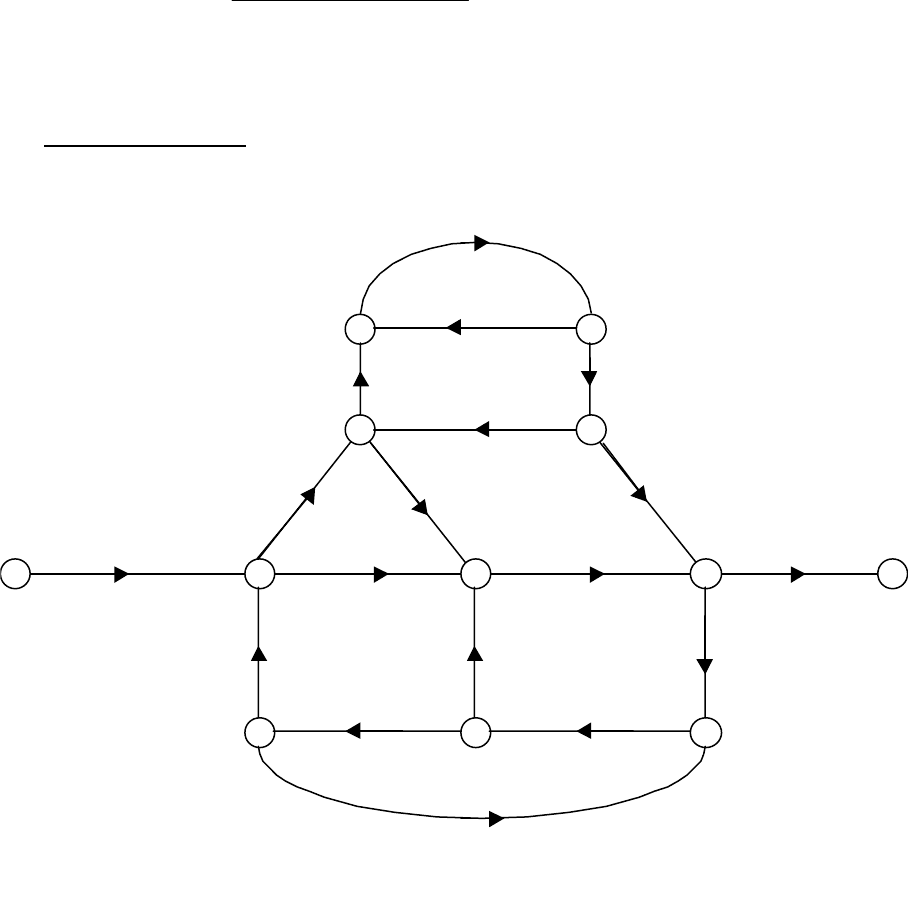
Этой схеме соответствует граф, представленный на рис. 2.38.

-1

Рис. 2.38. Граф системы с перекрёстными связями

Для этого графа:

• передаточная функция единственного прямого пути

WWW

пр

= ;

• передаточные функции контуров

3101

WWW −= ;

4202

WWW

;

• главный определитель

4231

1 WWWW −

=Δ ;

• определитель прямого пути

=Δ ;

• искомая передаточная функция

4231

1 WWWW

−+

ПРИМЕР 2.8-2.

Найти передаточную функцию между точками

B для графа, приведённого на рис. 2.39.

Рис. 2.39. Граф системы

• Передаточные функции прямых путей:

·W

;

·W

;

·W

• Передаточные функции контуров:

= W

·W

;

= W

·W

;

= W

·W

;

= W

·W

;

= W

·W

;

= W

·W

• Произведения передаточных функций непересекающихся пар конту-

ров:

·W

; W

·W

; W

·W

; W

·W

; W

·W

; W

·W

; W

·W

• Непересекающихся троек контуров нет.

• Определитель графа:

Δ=1- W

- W

+ W

·W

• Миноры определителя графа:

=1-W

-W

·W

;

=1-W

-W

·W

;

=1-W

• Результирующая передаточная функция

+Δ

5544332211

WWWWW

2.9. Устойчивость систем

2.9.1. Асимптотические свойства собственного движения и весовой

матрицы линейной системы

Пусть нелинейное дифференциальное уравнение состояния имеет

вид

}),(),({)(

ttutxFtx

. (2.9-1)

Пусть также

)(

– некоторая заданная (номинальная) функция време-

ни и

)(

– некоторый номинальный вектор начальных условий.

Решение

)(

является устойчивым в смысле Ляпунова, если для

любого

t и для любого 0>

существует 0),(

такое, что при

≤

− )()(

000

txtx

(2.9-2)

удовлетворяется неравенство

≤

− )()(

txtx

. (2.9-3)

Норма вектора

в простейшем случае совпадает с его евклидовой

длиной

2/1

)(

∑

. (2.9-4)

Возможно так же использование и других форм нормы, например

∑

xxxx

;max

. (2.9-5)

Введение нормы в пространстве состояний дает возможность ввести

понятие близости точек пространства. Устойчивость в смысле Ляпунова

гарантирует, что состояние

)(tx

не отклоняется далеко от «номинально-

го» режима

)(

при начальном состоянии )(

, достаточно близком к

номинальному начальному состоянию

)(

Решение

)(

называется асимптотически устойчивым, если оно

устойчиво в смысле Ляпунова, и для любого

t существует такое )(

что при

≤

− )()(

000

txtx

(2.9-6)

выполняется условие

0)()(lim

−

∞→

txtx

. (2.9-7)

Решение

)(

является асимптотически устойчивым в целом, если оно

устойчиво по Ляпунову, и для любых

t и )(

0)()(lim

−

∞→

txtx

. (2.9-8)

Применительно к нелинейным системам, вследствие сложности

характерных для них явлений, обсуждается обычно устойчивость реше-

ний. В линейных системах ситуация проще, и в этом случае целесооб-

разнее говорить об устойчивости уже не решения, а самой системы.

Пусть дано уравнение системы

)()()()()(

tutBtxtAtx

rrr

, (2.9-9)

и для

t , )(

и )(

, при

tt ≥ известно )(

, то есть спра-

ведливо уравнение

)()()()()(

tutBtxtAtx

rrr

. (2.9-10)

Естественно, что при других начальных условиях

)(

решение )(

будет другим

)()()()()(

tutBtxtAtx

rrr

. (2.9-11)

Вычтем из (2.9-11) уравнение (2.9-10):

{}{}

)()()()()(

0101

txtxtAtxtx

CCCC

rrrr

−=−

(2.9-12)

Обозначив,

)()()(

txtxtx

−=

при начальных условиях

)()()(

00010

txtxtx

−=

получим уравнение

)()()(

txtAtx

= , при

)(

txx

. (2.9-13)

Таким образом, понятие устойчивости решения можно свести к понятию

устойчивости линейной системы.

Линейная система устойчива в определенном смысле (по Ляпу-

нову, асимптотически, или асимптотически в целом), если тривиаль-

ное решение

0)(

≡tx

устойчиво в этом смысле.

Линейная система асимптотически устойчива тогда и только

тогда, когда она асимптотически устойчива в целом.

Таким образом, исследование вопроса устойчивости решений ли-

нейной неавтономной системы сводится к исследованию решения соот-

ветствующего однородного дифференциального уравнения, которое оп-

ределяется матрицей

)(t

и имеет вид:

)(),()(

txtttx

Φ=

; (2.9-14)

)(),()(

txtttCy

Φ=

. (2.9-15)

Рассмотрим три возможных случая.

),(

ttΦ – ограниченная матрица в интервале ),[

∞

t , то есть сущест-

вует такое положительное число

М что

...,2,1,;,),(

njittMtt

≥

≤

Тогда получаем, что

)(max)(

txMntx

≤

и условие устойчивости выполняется, если взять, например,

≤ .

2. Переходная матрица удовлетворяет условию

0),(lim

∞→

При этом движение, а значит, и сама система являются асимптотически

устойчивыми.

),(

ttΦ – неограниченная матрица в интервале ),[

∞

t . При этом дви-

жение неустойчиво, так как для любого

0)(

≠

∞

∞→

)(lim tx

Это означает и неустойчивость самой системы.

Если система является наблюдаемой и управляемой, (эти понятия

будут рассмотрены в п.п. 3.2, 3.3), то устойчивость системы можно ис-

следовать с помощью весовой функции. Система асимптотически устой-

чива, если

0),(lim

∞→

Итак, линейная система является асимптотически устойчивой, ес-

ли ее переходная матрица с течением времени стремится к нулевой

матрице. Для стационарных систем, то есть для систем с постоянными

параметрами, это условие эквивалентно требованию, чтобы все собст-

венные числа матрицы

имели отрицательные действительные части,

то есть лежали в левой полуплоскости плоскости комплексной перемен-

ной

. Это следует из формы представления переходной матрицы че-

рез собственные числа и правые и левые собственные векторы матрицы

в соответствии с (2.4-28). Таким образом, анализ устойчивости сис-

темы может быть сведен к анализу расположения собственных чисел

матрицы

, или, что, то же самое, расположения полюсов передаточной

функции полностью управляемой и наблюдаемой системы.

В теории автоматического управления разработан ряд методов,

называемых критериями устойчивости, позволяющих проанализировать

расположение собственных чисел относительно мнимой оси плоскости

, и не требующих при этом точного решения соответствующего харак-

теристического уравнения. К первой группе этих методов относятся, так

называемые, алгебраические критерии, которые путем элементарных

вычислений по коэффициентам характеристического полинома позво-

ляют проанализировать устойчивость исследуемой системы с извест-

ными значениями ее параметров.

2.9.2. Необходимое условие устойчивости

Для устойчивости системы с характеристическим полиномом

aaaa

−

...)( (2.9-16)

необходимо, чтобы при 0

>a все коэффициенты характеристического

полинома были положительны, то есть

a при ni ,...,2,1

Докажем это утверждение. Если

,,,,,,

- нули характеристи-

ческого полинома (корни характеристического уравнения

0)( =

), то

(2.9-16) может быть записано в виде

)(...))(()(

21 n

−

−−= . (2.9-17)

Если

- вещественный корень в левой полуплоскости, то есть

−= ( 0>

- положительное вещественное число), то

)()(

=−

и произведение таких сомножителей даст полином только с положи-

тельными коэффициентами.

Пусть

- комплексный корень в левой полуплоскости, то есть

iii

+−= ( 0>

). Тогда при всех вещественных коэффициентах

характеристического полинома среди его нулей должен быть комплекс-

но сопряжённый:

iii

−−=

. Произведение двух соответствующих

сомножителей даст полином второй степени с положительными коэф-

фициентами:

)2))((

222

iiiii

+=−−

Следует обратить внимание на то, что рассмотренное условие ус-

тойчивости не является достаточным. Если среди коэффициентов ха-

рактеристического полинома имеются отрицательные, то это означает,

что соответствующая система неустойчива. Если все коэффициенты по-

ложительны, то система может быть как устойчивой, так и неустойчивой.

В этом случае необходим дополнительный анализ.

2.9.3. Критерий устойчивости Гурвица.

Пусть характеристический полином некоторой системы имеет вид

(2.9-16). Сопоставим этому полиному матрицу Гурвица:

⎥

⎦

⎤

⎢

⎣

⎡

−

aaa

420

531

...000

0...000

..................

00...0

00...

. (2.9-18)

По главной диагонали стоят коэффициенты полинома, остальные

элементы строятся по следующему принципу: вверх от диагонального

элемента ставятся коэффициенты полинома в порядке возрастания ин-

дексов, вниз - коэффициенты полинома в порядке убывания индексов.

Элементы, требующие индексов, больших степени полинома, или отри-

цательных, устанавливаются нулевыми.

Критерий Гурвица.

Для устойчивости системы необходимо и достаточно чтобы при

>0 были положительны все (n) главные миноры матрицы Гурвица.

Рассмотрим примеры конкретизации критерия Гурвица для простейших

случаев.

•

1=n .

Запишем дифференциальное уравнение

=+⋅ ya

и характеристическое уравнение

=+ aa

В данном случае применение критерия Гурвица даёт тривиальный

результат

0,0

>> aа

•

2=n .

Запишем дифференциальное уравнение