Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.


61
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
110
110
111
V
.
Присоединенная матрица для
T
A
()
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
2
2
2
1
001
λλ
λλλ
λ
λ
d
I .
Левые собственные векторы
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
5.0
5.0
0
;
5.0
5.0
0
;
1
0
1
321
ddd
rrr
.
Базовые матрицы
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
000
000
101
11
T
dv
r
r
;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
5.05.00
5.05.00
5.05.00
22
T
dv
r
r
;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
5.05.00
5.05.00
5.05.00
33
T
dv
r
r
.
Вычислим коэффициенты суммы (2.6-9):
⎥
⎦
⎤
⎢
⎣
⎡
−−
=
00
11
11
BdvC
T
r
r
;
⎥
⎦
⎤
⎢
⎣
⎡
=
5.05.0
5.05.0
22
BdvC
T
r
r
;
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
5.05.0
5.05.0
33
BdvC
T
r
r
и получим результат, естественно, совпадающий с уже полученным
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⋅
+
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
−
+
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
11
11
2
1
1
1
11
11
2
1
1
1
00
11
1
)(
ppp
pW
uy
.
Практически без дополнительных выкладок получаем

62
tt
y
eetw
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
−
+⋅
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
−−
=
11
11
2
1
11
11
2
1
00
11
)( .
Интегрируя весовую функцию, получаем матричную переходную функ-
цию
()()
()()
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−+−
−+−+−+−
=
−−
−−
tttt
tttt
y
eeee
eeteet
tH
2
1
2
2
1
2
1
2
2
1
)(
.
2.6.2. Основные свойства передаточных функций
Понятие передаточной функции лежит в основе классической теории ав-
томатического регулирования. В связи с этим ниже перечисляются ос-
новные её свойства, используемые при анализе систем автоматического
управления.
1. Элемент
i -й строки и
j
-го столбца матричной передаточной функции
равен отношению изображения
i -й координаты вектора выхода к
j
-ой
координате вектора управления при нулевых начальных условиях:
()
)(
)(
pU
pY
pW
j
i
ij
= . (2.6-11)
Таким образом,
∑
=
=
nu
j
jiji
pUpWpY
1
)()()( . (2.6-12)
2. Для стационарных объектов с сосредоточенными параметрами эле-
менты матричной передаточной функции - это дробно-рациональные
функции комплексной переменной
p
:
.
...
...
)(
)(
)(
1
10
1
10
n
nn
m
mm
ij
ij
ij
apapa
bpbpb
pQ
pR
pW
+++
+++
==
−
−
(2.6.13)
3. По известной передаточной функции легко восстанавливаются соот-
ветствующие дифференциальные уравнения. По данным предыдущего
примера

63
)(
)1(
1
)(
)1(
1
)(
2
2
1
2
2
1
pU
pp
pU
pp
pp
pY
−
+
−
+
+
−
= .
После приведения к общему знаменателю получаем
()
(
)
)()()()(
2111
2
11
3
pUpUppUpUpppYpYp
+
+
+
−=− ,
и в результате имеем
()
)()()()()(
211111
tututututyty
+
+
+−
=
−
&&&&&&&
.
4. Знаменатель передаточной функции - это соответствующий характе-
ристический полином. Полюсы передаточной функции - это корни соот-
ветствующего характеристического полинома.
5. Поскольку весовая функция является оригиналом для передаточной,
то при всех различных полюсах
tp
n
l
lij
l
eCtw
∑
=
=
1
)( , (2.6.14)
где
l
p - полюсы функции;
∏
∏
≠=
=
−
−
⋅==
n
lvv
m
v
ij
l
vl
vl
l
ij
l
rp
rp
a
b
pQ
pR
C
,1
1
'
)(
)(
)(
)(
0
0
; (2.6.15)
00
,ab - коэффициенты при старших степенях p числителя и знамена-
теля передаточной функции )(pW
ij
;
v
r - нули )(pW
ij
.
6. В физически реализуемых системах порядок числителя
m элемен-
тарной передаточной функции не может превышать порядка ее знаме-
нателя
n .
7. В простейших случаях элементарная передаточная функция может
быть непосредственно получена из соответствующего дифференциаль-
ного уравнения. Например, для динамического звена с уравнением
dt
tdu
Tty
dt
tdy
T
)(
)(
)(
=+
путем перехода к изображениям по Лапласу при нулевых начальных ус-
ловиях получаем
)()()(
p
U
p
T
p
Y
p
Y
p
T =+ ,
откуда
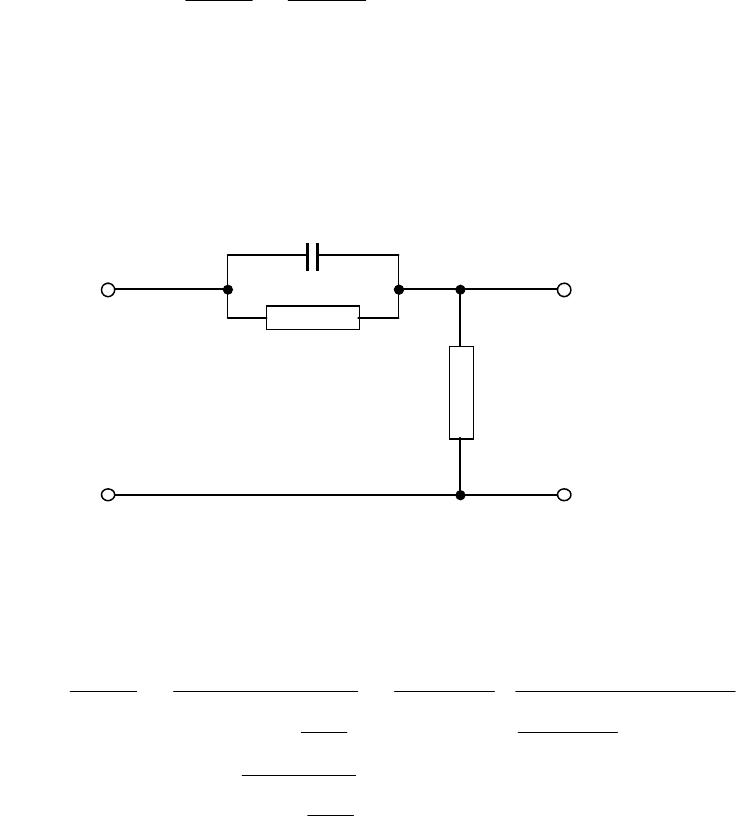
64
1)(
)(
)(
+
==
Tp
Tp
pU
pY
pW
.
При описании пассивных электрических цепей передаточные функции
могут вычисляться в соответствии с правилами электротехники с ис-
пользованием полных символических сопротивлений. Так, например,
для схемы, приведенной на рис.2.17,
R
1
С
R
2
U U
вых
=Y
Рис.2.17. Пассивное дифференцирующее звено
1
1
1
1
)(
)(
)(
1
21
2
1
21
2
1
1
2
2
+
+
+
⋅
+
=
+
⋅
+
==
CpR
RR
R
CpR
RR
R
pC
R
pC
R
R
R
pU
pY
pW
.
65
2.7. Комплексный передаточный коэффициент
2.7.1. Способы определения понятия «Комплексный передаточный
коэффициент»
Известно несколько подходов к введению понятия «Комплексный
передаточный коэффициент». Рассмотрим основные из них.
♦ Формальная замена комплексной переменной в передаточной функ-
ции.
Изображения по Лапласу вектора выхода и вектора управления
связаны между собой с помощью передаточной функции
)()()( pUpWpY
v
v
= . (2.7-1)
Если в этом равенстве комплексную переменную
p
принять чисто мни-
мой величиной
ω
j
p
= , то формально получаем следующее равенство
)()()(
ωωω
jUjWjY
v
v
= . (2.7-2)
Здесь комплексный передаточный коэффициент )(
ω
j
W определяется
формально:
ω
ω
jp
pWjW
=
= |)()( .
Строго говоря, эта замена не всегда правомерна.
♦ Использование преобразования Фурье
Прямое и обратное преобразования Лапласа выглядят следую-
щим образом:
∫∫
∞
+
−
−
==
0
)(
2
1
)( ;)()(
ω
ω
π
jC
jC
ptpt
dpepY
j
tydtetypY (2.7-3)
Преобразование Лапласа существует тогда, когда вещественная часть
комплексной переменной
p
удовлетворяет неравенству
C
σ
σ
> .
Если функция
)(ty , ),0[ ∞∈t является односторонней и абсолютно ин-
тегрируемой, т.е.
∞<
∫
∞
0
)( dtty , то её абсцисса абсолютной сходимости
C
σ
<0, и можно принять
ω
j
p
= ( 0
=
σ
). В этом случае прямое преобра-
зование Лапласа совпадает с прямым преобразованием Фурье:
∫
∞
−
=
0
)()( dtetyjY
tj
ω
ω
. (2.7-4)
Практически столь же просто обратное преобразование Лапласа пре-
вращается в обратное преобразование Фурье:

66
. )(
2
1
)(
)()(
2
1
)(
∫
∫
∞+
∞−
∞+
∞−
∞
=
⇒=
ωω
π
ωω
π
ω
dejYty
jdejY
j
ty
tj
j
j
tj
(2.7-5)
Таким образом, если
)()( );()()( txCtytuBtxAtx
r
r
r
r
&
r
=+= и если
функции
)(tx
r
, )(ty
r
и )(tu
r
абсолютно интегрируемы, то можно к указан-
ным уравнениям применить не только преобразование Лапласа, но и
преобразование Фурье:
);()()(
ωωωω
jUBjXAjXj
r
rr
+=
);()()(
1
ωωω
jUBAEjjX
r
r
⋅⋅−=
−
);()()(
ωωω
jUjWjX
x
r
r
⋅=
.)()(
1
BAEjCjW
y
−
−
⋅=
ω
ω
(2.7-6)
Функция
BAEjCjW
y
1
)()(
−
−=
ω
ω
называется комплексным передаточ-
ным коэффициентом, или частотной функцией соответствующего дина-
мического звена или системы. Аналогично передаточной функции, она
может быть выражена через левые и правые собственные, векторы мат-
рицы
А
векторно-матричного дифференциального уравнения этого зве-
на или системы:
∑
=
−
=
n
i
i
T
ii
j
BdvC
jW
1
)(
λω
ω
v
r
. (2.7-7)
2.7.2. Реакция динамических звеньев на гармонические воздействия
Рассмотрим реакцию системы
)()()( tubtxAtx ⋅+⋅=
r
rr
со скалярным управлением на гармоническое воздействие
tj
m
tj
m
m
e
U
e
U
tCosUtu
ωω
ω
−
+⋅=⋅=
22
)( . (2.7-8)
Каждое из слагаемых последнего выражения вызывает свою реакцию,
то есть,
)()()(
21
txtxtx
r
rr
+= . (2.7-9)

67
В силу линейности рассматриваемых систем применим принцип супер-
позиции, и достаточно определить реакцию на первое слагаемое
tj
m
e
U
tu
ω
⋅=
2
)(
1
. (2.7-10)
Ищем
)(
1
tx
r
в виде:
tj
e
X
tx
ω
⋅=
2
)(
1
1
o
r
r
, (2.7-11)
где
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
o
o
o
o
M
r
n
X
X
X
X
1
12
11
,
а
o
i
X - комплексные амплитуды по координатам вектора состояния:
i
j
i
i
eXX
ϕ
max
=
o
. (2.7-12)
Подставим
)(
1
tx
r
и )(
1
tu
r
в исходное дифференциальное уравнение и
проведём элементарные преобразования:
tj
m
tjtj
e
U
be
X
Ae
X
dt
d
ωωω
⋅⋅+⋅⋅=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
⋅
222
1
1
r
r
r
o
o
;
tj
m
tjtj
eUbeXAejX
ωωω
ω
⋅⋅+⋅⋅=⋅⋅
r
rr
oo
1
1
;
m
UbXAjX ⋅=⋅−⋅
r
rr
oo
1
1
ω
;
,)(
1
1
m
UbAEjX ⋅⋅−=
−
r
r
o
ω
то есть:
m
UjWX ⋅= )(
1
ω
o
r
, (2.7-13)
где матричный комплексный передаточный коэффициент
bAEjjW
r
1
)()(
−
−=
ωω
,
что совпадает с (2.7-6).
68
Аналогичным образом можно получить реакцию на вторую составляю-
щую входного сигнала
tj
m
e
U
tu
ω
−
⋅=
2
)(
2
:
m
UjWX ⋅−= )(
2
ω
o
r
. (2.7-14)
Полная реакция системы на гармоническое воздействие (2.7-8) в соот-
ветствии с (2.7-13)) , ((2.7-14)) и ((2.7-9)
=
−
+=
− tj
m
tj
m
e
UjW
e
UjW
tx
ωω
ω
ω
2
)(
2
)(
)(
r
m
nn
U
tjW
tjW
tjW
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
=
)cos()(
..............
)cos()(
)cos()(
22
11
ϕωω
ϕωω
ϕωω
.
Таким образом, элемент матричной функции
)(
ω
j
W , которая, по
понятным теперь причинам, называется частотной функцией, определя-
ется как отношение вынужденной гармонической составляющей (част-
ное решение неоднородного дифференциального уравнения) к гармони-
ческому входному воздействию при условии записи их в символической
форме. Комплексный передаточный коэффициент определяет измене-
ние в зависимости от частоты амплитуды и фазы гармонического сигна-
ла при
прохождении его от вектора управления до каждой из координат
вектора состояния или вектора выхода:
i
j
m
i
i
e
U
X
jW
ϕ
ω
⋅=
max
)( . (2.7-15)
Модуль
)(
ω
j
W определяет отношение амплитуд:
m
i
i
U
X
jW
max
)( =
ω
, (2.7-16)
а фаза – сдвиг по фазе между входным и выходным гармоническими
сигналами:
ii
jW
ϕ
ω
=
))(arg( . (2.7-17)
2.7.3. Частотные характеристики
Элементы матричной частотной функции связывают между собой
соответствующие координаты векторов входа и управления:
69
)(
)(
)(
ω
ω
ω
jU
jY
jW
k
i
ik
= . (2.7-18)
Такие скалярные функции принято иллюстрировать графическими час-
тотными характеристиками:
– амплитудно-фазовой характеристикой (АФХ), построенной в поляр-
ной системе координат {модуль, фаза}; можно рассматривать и соот-
ветствующую декартову систему координат, по осям которой откла-
дываются вещественная и мнимая части годографа вектора
)(
ω
j
W ;
– логарифмическими частотными характеристиками (ЛЧХ) - амплитуд-
но-частотной (ЛАЧХ), построенной в осях
|)(|
ω
j
W в децибелах, -
ω
в логарифмическом масштабе, и фазочастотной (ЛФЧХ), построен-
ной в осях фаза - ω в логарифмическом масштабе
Модуль частотной функции в децибелах определяется в соответствии с
выражением
|)(|lg20|)(|
ω
∂
σ
ω
jWjW
ikik
= . (2.7-19)
В качестве примера для звена
3
2
108.0
14
)(
p
k
p
p
pW
⋅
⎟
⎠
⎞
⎜
⎝
⎛
+
+
=
приведены
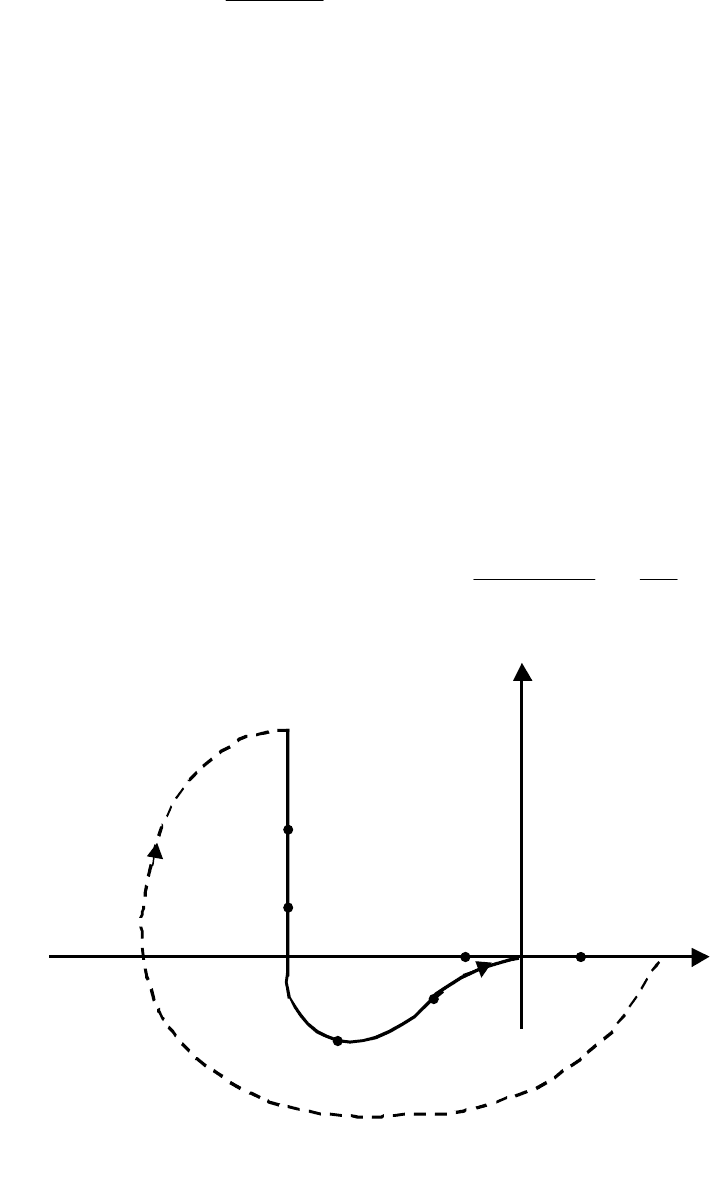
АФХ (рис.2.18) и ЛЧХ (рис.2.19).
ω
4
ω
3
ω
2
ω
1
ω=8
-1 1
+
+ j
Рис 2.18. Амплитудно-фазовая характеристика
70
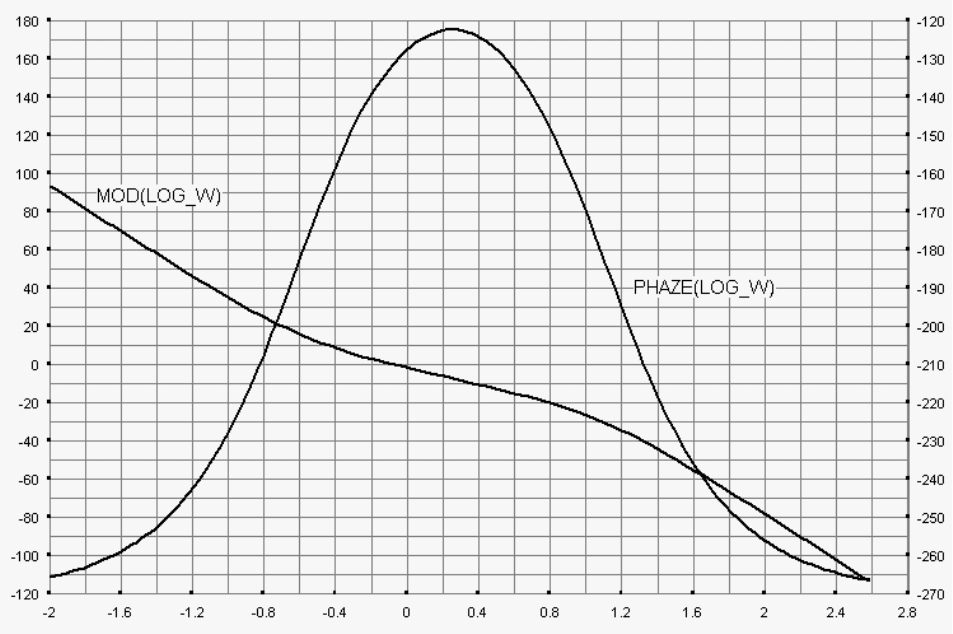
Рис 2.19. Логарифмические амплитудно-частотная
и фазочастотная характеристики
В учебной литературе по теории автоматического управления достаточ-
но подробно рассматривается методика построения частотных характе-
ристик типовых или более общего вида динамических звеньев и систем.
Поэтому в настоящем пособии эти вопросы не затрагиваются.
