Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

201
2
x
)
u
v
yx
=
1
50 объект
72
10
9
7
34
2
ˆ
x
Рис. 3.20. Структурная схема полной
системы для примера 3.12-2
3.12.4.3. Система со скалярными входом и выходом и наблюда-
телем пониженного порядка
Структурная схема объекта представлена на рис. 3.21.
Рис. 3.21. Структурная схема объекта
y
2
y
1
x
3
u
x
1
x
2
x
4
2
Ему соответствуют матрицы
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
2100
0100
0110
0010
A
;
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
0
1
0
0
B
;
⎥
⎦
⎤
⎢
⎣
⎡
=
1000
0001
C
.
Требуется рассчитать управление и построить наблюдатель минималь-
ного порядка.
Объект имеет собственные числа
202
2;1;1;0
4321
−
=
−
=+==
λ
λ
λ
λ
и характеристический полином
λ
λ
λ
λ
λ
ϕ
22)(
234
−
−
+
=
A
.
Найдём матрицу управляемости:
[]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−−
==
7310
1111
1010
0100
32
BABAABBU .
Её определитель
6det −=U , то есть отличен от нуля. Это означает, что
объект управляем. Рассчитаем закон управления (матрицу обратной
связи), обеспечивающий следующие желаемые собственные числа
замкнутой системы:
1
4321
−
=
==
=
зззз
λ
λ
λ
λ
,
которым соответствует характеристический полином
1464)(
234
+
+
++=
λ
λ
λ
λ
λ
ϕ
c
A
.
Таким образом, имея коэффициенты характеристических полиномов
объекта и желаемой замкнутой системы
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
1
4
6
4
;
0
2
1
2
γα
rr
,
можно в соответствии с (3.9-18) рассчитать матрицу обратной связи в
базисе УКП:
[
]
2761
−
−
−
−
=
U
L .
Чтобы найти эту матрицу в исходном базисе, нужно знать матрицу
H
U
перехода от исходного базиса к базису УКП. Так как столбцы этой мат-
рицы являются координатными столбцами векторов базиса
][u (УКП)
n
uuu
rrr
,...,,
21
в исходном базисе ][h , то, используя (3.8-6), можно запи-
сать:

203
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=+=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
==
1
1
1
0
;
0
1
0
0
1434 hhHhhh
buAubu
r
rr
r
r
α
;
.
0
0
0
2
;
1
2
2
1
321232
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=+=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=+=
hhHhhhHh
buAubuAu
r
rr
r
rr
αα
Таким образом, получаем:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
0110
1120
0120
0012
H
U и
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
=
−
3
4
1
3
1
0
3
2
1
3
1
0
3
1
1
3
1
0
6
1
0
6
1
2
1
1
H
U .
В соответствии с (3.9-12)
[]
6
1
2
6
29
2
1
1
−−−−==≡
−
HUH
LLL U .
В соответствии с (3.6-8)
⎥
⎦
⎤
⎢
⎣
⎡
−
==
0110
0012
HU
CC U .
Используя (3.8-22) запишем передаточные функции:
)1)(1(
1
)(
1
−+
=
ppp
pW
yu
;
)2)(1(
1
)(
2
++
=
pp
pW
yu
;
4
)1(
2
)(
1
+
+
=
p
p
kpW
v
yv
;
4
)1(
)1(
)(
2
+
−
=
p
pp
kpW
v
yv
.
В замкнутой системе будет обеспечена единичная статика по координа-
те
1
y , если задать
2
1
=
v
k .
Теперь перейдём к синтезу наблюдателя. Построим матрицу
N
~
:
204
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
2100
0010
1000
0001
~
CA
C
N
.
Ранг этой матрицы равен четырём, то есть, порядку объекта. Так как
старшая степень блока
CA, входящего в неё, равна единице, то индекс
наблюдаемости
2
=
ν
и порядок наблюдателя в соответствии с (3.11-54)
1=s . Это означает, что в данном случае может быть построен наблюда-
тель первого порядка. Зададим единственное собственное число на-
блюдателя
4
1
−=
N
λ
. Отсюда сразу определяется матрица наблюдателя
4−=
q
L .
Раскроем матричное уравнение Люенбергера (3.11-48), имея вви-
ду, что в данном случае матрица
q
C имеет размер ]14[
×
. Для этого за-
пишем подробно каждое слагаемое:
[]
[]
;20
2100
0100
0110
0010
443221
4321
qqqqqq
qqqqq
cccccc
ccccAC
−+−+=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
=
[
]
4321
4444
qqqqq
q
ccccC
−
−−−=L ;
[] [ ]
2121
00
1000
0001
yyyy
y
ggggCG =
⎥
⎦
⎤
⎢
⎣
⎡
= .
С учётом этих выражений матричное уравнение Люенбергера можно
представить в виде системы скалярных уравнений:
.2
;03
;05
;4
24
432
21
11
yq
qqq
qq
yq
gc
ccc
cc
gc
=
=++
=+
=
Аналогично поступим со вторым матричным уравнением системы (3.11-
53), учитывая вытекающие из этого уравнения размерности матриц
χ
и
η
:

205
[
]
;
4321 qqqqq
ccccC
χ
χ
χ
χ
χ
=
[] [ ]
2121
00
1000
0001
ηηηηη
=
⎥
⎦
⎤
⎢
⎣
⎡
=C
и
.
;
;
;
424
33
22
111
lc
lc
lc
lc
q
q
q
q
=+
=
=
=+
ηχ
χ
χ
η
χ
Таким образом, получено восемь уравнений при наличии девяти неиз-
вестных
χ
η
η
,,,,,,,,
21214321 yyqqqq
ggcccc . Примем 1=
χ
. После этого
легко находятся остальные неизвестные:
;
6
65
2
6
29
6
145
⎥
⎦
⎤
⎢
⎣
⎡
−−=
q
C
.
3
65
3
290
;11
3
74
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−−=
y
G
η
В соответствии с (3.11-44) вычисляем
2
−
== BCG
q
u
.
В результате можем записать уравнения регулятора совместно на-
блюдателем Люенбергера минимального (первого) порядка:
.)(11)(
3
74
)()(
2
1
)(
;)(
3
65
)(
3
290
)(2)(4)(
21
21
tytytqtvtu
tytytutqtq
−−+=
++−−=
)
r
)
r
&
)
r
Этим уравнениям соответствует структурная схема системы управле-
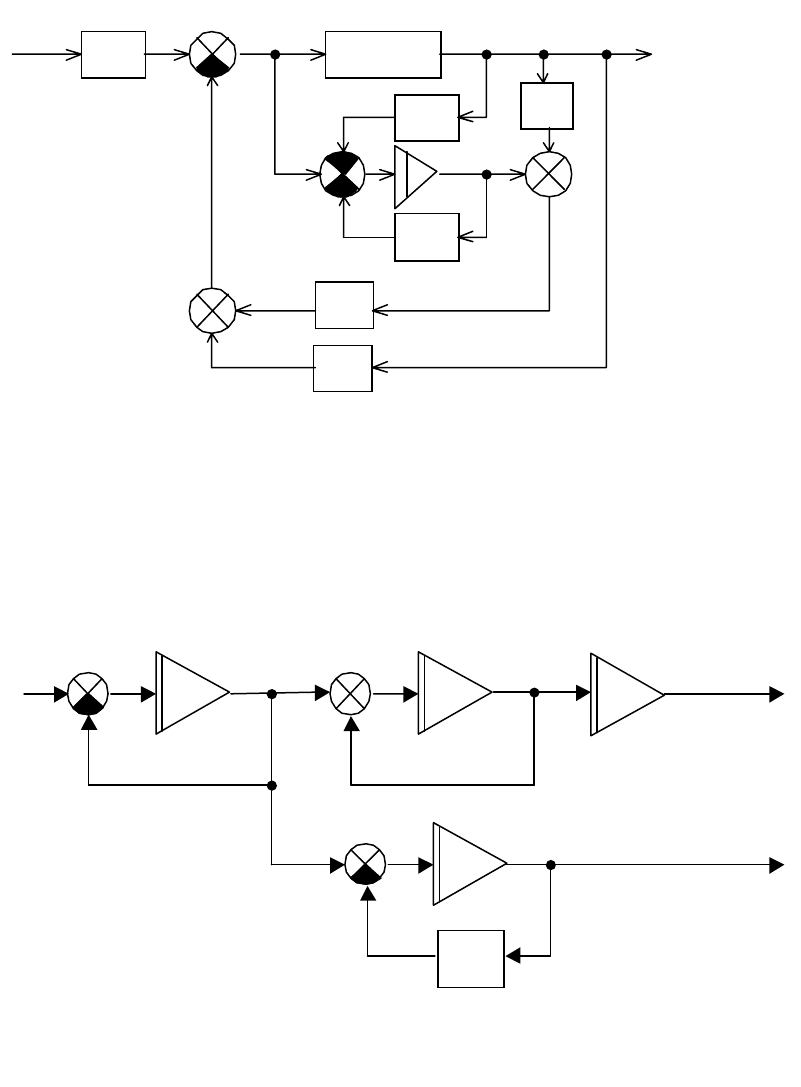
ния, приведённая на рис. 3.22.
206
Рис. 3.22. Структурная схема системы
управления.
y
1
u
y
2
v
ОБЪЕКТ
2
4
3
65
3
290
11
3
74
3.12.4.4. Многомерная система с разделением каналов и наблю-
дателем минимального порядка
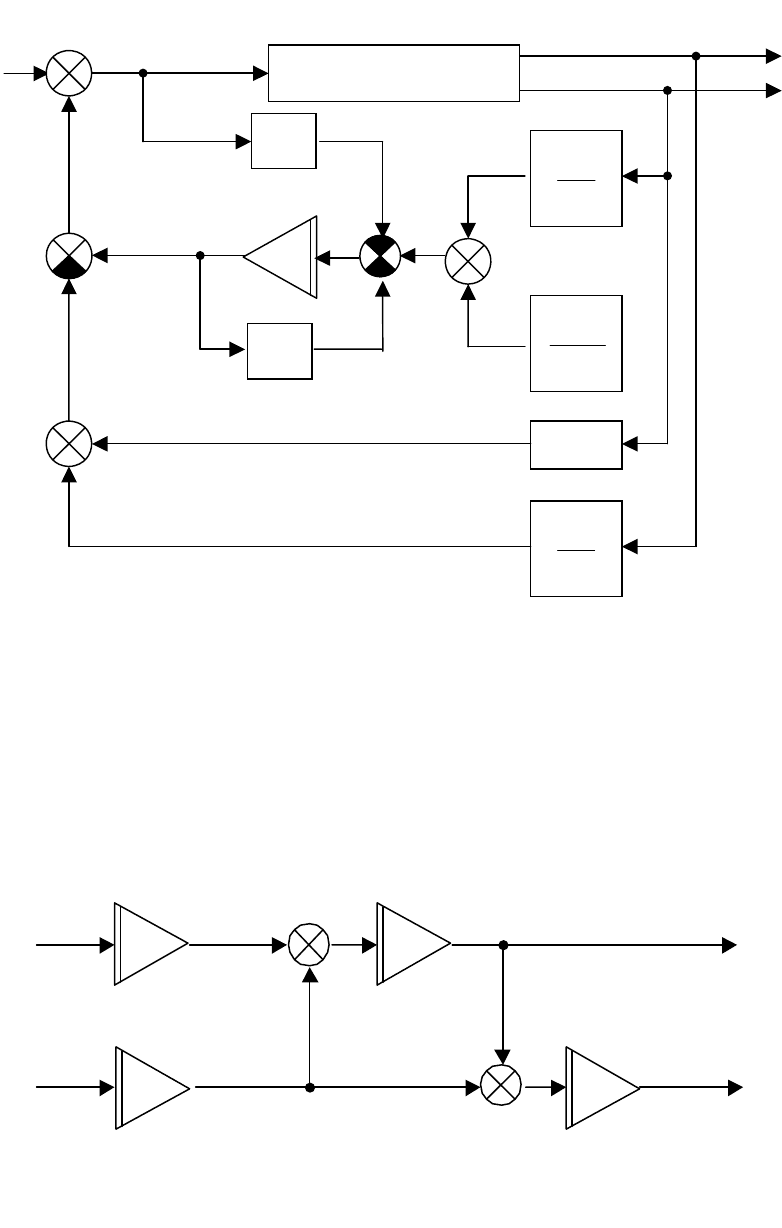
Задан объект, представленный структурной схемой на рис. 3.23.
Рис. 3.23. Структурная схема объекта
2
u
x
3
2
x
4
y
2
y
1
1
u
x
1
x
2
Объекту соответствуют матрицы
.
1000
0100
;
00
00
10
01
;
0110
0011
0000
0000
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
= CBA
207
Расчёт матриц управляемости и наблюдаемости определяет объект как
полностью управляемый и наблюдаемый.
I. Синтез управления в соответствии с п.3.10.
1. Расчёт чисел
i
m :
[
]
[
]
[] []
.10;00
;11;00
1
2
0
2
1
1
0
1
==
=
=
BACBAC
BACBAC
Отсюда следует
2
21
== mm .
2. Вычисление матриц
∗∗
BF , .
При
2
21
== mm
⎥
⎦
⎤
⎢
⎣
⎡
==
⎥
⎦
⎤
⎢
⎣
⎡
−−
=−=
∗∗
10
11
;
0011
0000
2
CABBCAF .
3. Расчёт
1−
∗
B .
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
∗
10
11
1
B .
Поскольку эта матрица существует, задача разделения каналов имеет
решение.
4. Вычисление матриц
∨∨
BA, .
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−−
=+=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
==
∗
∨∨
−
∗
∨
0110
0011
0011
0011
;
00
00
10
11
1
FBAABBB .
В соответствии с (3.10-13) этим матрицам отвечают уравнения
.
;
;
;
324
213
2212
21211
xxx
xxx
qxxx
qqxxx
+=
+=
+−−=
−
++
=
&
&
&
&
Соответственно этим уравнениям
,
;
2
)2(
4
1
)2(
3
qx
qx
=
=
208
то есть действительно, исходная система разбита на две независимые
подсистемы, состоящие из последовательно включённых интеграторов.
5. Построение матрицы
e
F .
В данном случае
[]
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
−
==
∨∨
∨
∨∨
∨
0100
0001
1001
1011
2211
bbAbbA
e
rrrr
F .
Новому базису соответствуют матрицы
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
0100
0001
;
10
00
01
00
;
0000
1000
0000
0010
fff
CBA .
6. Расчёт матрицы обратной связи промежуточной системы в базисе
][f .
Зададим желаемые собственные числа для первого канала
11
2,11
j±−=
λ
и для второго канала
55
2,12
j±−=
λ
.
Им соответствуют характеристические полиномы
.5010)(
;22)(
2
2
2
1
++=
+
+=
λλλϕ
λ
λ
λ
ϕ
Получаем строки матрицы
f
L :
[]
[
]
1050;22
21
−
−
=−−=
ff
ll
и саму матрицу
⎥
⎦
⎤
⎢
⎣
⎡
−−
−−
=
105000
0022
f
L .
Пункты 7 и 8 итогового алгоритма расчёта управления для данного
случая не нужны, так как в рассматриваемом примере сумма порядков
подсистем
21
mm + равна порядку объекта, и матрица
00
A отсутствует.
9. Расчёт матрицы при командном сигнале.
Потребуем выполнения равенства
209
1)0()0(
2211
=
=
yvyv
WW .
Тогда
50;2
21
=
=
∨∨
vv
kk
и
⎥
⎦
⎤
⎢
⎣
⎡
=
∨
500
02
v
k .
10. Расчёт матрицы обратной связи промежуточной системы в исход-
ном базисе.
.
5010100
0222
0110
1000
0011
0100
105000
0022
1
⎥
⎦
⎤
⎢
⎣
⎡
−−−
−−−
=
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−−
−−
==
−
∨
ef
LL F
11. Расчёт результирующей матрицы обратной связи.
⎥
⎦
⎤
⎢
⎣
⎡
−−−−
−
=+=
∨
∗
−
∗
5010111
50891
)(
1
LFBL .
12. Расчёт матрицы передаточных коэффициентов по вектору ко-
мандных сигналов
⎥
⎦
⎤
⎢
⎣
⎡
−
==
∨
−
∗
500
502
1 vv
kBk .
Таким образом, получено управление, использующее координаты
вектора состояния объекта:
.50501011
;5025089
243212
2143211
vxxxxu
vvxxxxu
+−−−−=
−
+
+++−=
II. Синтез наблюдателя в соответствии с п.3.11.3.
1. Расчёт индекса наблюдаемости.
Строим матрицу
N
~
:
210
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
−
0110
0011
1000
0100
~
12
CA
C
N
.
Эта матрица имеет 4 линейно независимые строки, её детерминант от-
личен от нуля, значит
nNrank == 4)
~
( . Следовательно, индекс наблю-
даемости объекта
2=
ν
и размерность наблюдателя 2=s .
2. Задание динамики наблюдателя.
Зададим собственные числа
10
2,1
−
=
N
λ
. Соответственно матрица ди-
намики наблюдателя
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
100
010
q
L .
3. Решение системы матричных уравнений (3,11-53).
Матрица
q
C имеет размерность ]42[
×
, матрицы
y
G ,
γ
,
η
- ]22[
×
.
Следовательно, система скалярных уравнений, соответствующая
системе матричных уравнений (3,11-53), содержит 16 уравнений и 20
неизвестных. Таким образом, мы имеем право произвольно задать 4
«лишних» неизвестных. Зададим матрицу
χ
единичной, то есть
⎥
⎦
⎤
⎢
⎣
⎡
=
10
01
χ
.
С учётом этого из первого матричного
уравнения (3.11-53) получим следующую систему уравнений:
.10)8;10)4
;10)7;10)3
;010)6;010)2
;010)5;010)1
22241214
212324111314
222423121413
21231113
gcgc
gccgcc
cccccc
cccc
qq
qqqq
qqqqqq
qqqq
==
=+=+
=++=++
=
+
=+
Второе матричное уравнение (3.11-53) преобразуется в систему скаляр-
ных уравнений
;11)14;9)10
;1)13;1)9
2212
2111
−==
−
=
−=
qq
qq
cc
cc
;10)15;8)11
21231113
−
=
+
=+
η
η
qq
cc
