Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

151
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
=
=
=
=
−
.
............
;
;
1
2
3
2
1
be
be
be
be
n
n
r
r
r
r
r
r
r
r
A
A
A
(3.8-4)
Пусть характеристический полином оператора
A , а значит и его матри-
цы в преобразованном базисе имеет вид:
()
n1n
1nn
...
λ
λ
α
αλ
λ
λ
ϕ
+
+
++=
−
−
A
. (3.8-5)
Построим ещё один базис - базис ][u следующим образом:
{
{
{
{
{
{
{
{
{
{
{
{
.
;
;
;...
;...
;...
1
21
321
23
21
12
21
1
21
11
2
122
34
1433
23
1322
12
1211
e
n
ee
n
eee
n
e
n
e
n
e
n
e
n
e
n
e
n
e
n
e
n
n
e
n
e
n
e
n
bu
bbu
bbbu
bbbbu
bbbbu
bbbbu
nn
nn
n
r
r
rr
r
rrr
r
321
r
321
rrr
r
321
r
321
rrr
r
321
r
321
r
r
r
r
=
+=
++=
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
++++=
++++=
++++=
−
−
−−
−−
−−
−−
−−
−−
−−
−−
−
A
AA
AAA
AAA
AAA
α
αα
ααα
ααα
ααα
(3.8-6)
Проверим, действительно ли это базис? Матрица перехода от базиса
][e к базису ][u в соответствии с (3.4-4) и (3.4-5) имеет вид:
152
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
−−−
−−−
−−−
000...001
000...01
000...1
.....................
001...
01...
1...
1
12
5n4n3n
14n3n2n
123n2n1n
e
α
αα
ααα
αααα
α
α
α
α
α
U . (3.8-7)
Эта матрица является треугольной, её определитель равен про-
изведению диагональных элементов, умноженному на
n
)1(− , т.е. не ра-
вен нулю. Следовательно,
e
U не вырождена и система векторов
{}
n
uuu
rrr
...
21
действительно образует базис в пространстве X.
Вычислим теперь представление матрицы оператора
A в базисе
][u . При этом воспользуемся равенством
()
∑
=
=+++=
n
i
i
u
ik
u
nk
u
k
u
kk
uaua...uauaf
1
2211
)(
r
r
rr
r
AA
n
. (3.8-8)
С учётом (3.8-6)
()
()
.)( bb
bb
bbbbbu
A
rr
rr
r
r
r
r
r
r
n
nn1n
1n
1
n
nn1n
1n
1
n
1
E...
...
αϕ
αααα
αααα
−=
=−++++=
=−++++=
−
−
−
−
A
AAA
AAAA
(3.8-9)
По теореме Кэлли-Гамильтона
0)(
=
A
A
ϕ
, а значит bu
n
r
r
α
−=)(
1
A , от-
куда следует, что
n
u
n
a
α
−=
1
и 0
1
=
u
i
a при ni
<
, то есть
]0 ... 0 0[
1 n
α
−
=
T
u
a
r
. (3.8-10)
Далее действуем аналогичным образом:
{
n
u
n
u
nn
nn
bbbbbu
r
r
r
44444443444444421
r
r
r
r
r
112
2
1
1
2
1
...)(
−−−
−−
−++++=
αααα
AAAA , (3.8-11)
откуда следует, что
12212
;1 при 01
−
−=
<
<
=
=
n
u
n
u
i
u
ani , aa
α
, то есть
]0 ... 1 0[
12 −
−
=
n
T
u
a
α
r
.
Далее:
{
n
u
n
u
nn
nn
bbbbbu
r
r
r
44444443444444421
r
r
r
r
r
223
3
1
2
3
2
...)(
−−−
−−
−++++=
αααα
AAAA , (3.8-12)
153
откуда следует, что
2332313
;2 при 010
−
−
=
<
<
===
n
u
n
u
i
uu
ani; a; aa
α
,
то есть
]0 ... 0 1 0 0[
23 −
−
=
n
T
u
a
α
r
.
Вычислим предпоследний столбец матрицы:
{
n
n
u
u
n
bbbbu
r
r
r
444344421
r
r
r
r
221
2
1
2
)(
ααα
−++=
−
−
AAA , (3.8-13)
откуда следует, что
0
1
=
u
i,n-
a для 21
−
<
≤
ni , 1
12
=
−−
u
,nn
a , 0
11
=
u
,n-n-
a и
21
α
−=
u
n,n-
a , то есть
[]
21
01000
−−
−
⋅⋅⋅=
n
T
nu
a
α
r
.
Наконец,
()
nnn
uubbbu
r
r
r
r
r
r
1111
ααα
−=−+=
−
AA , (3.8-14)
откуда следует, что
21
,1и ,11 для0
α
−=
=
−
<
≤
=
−
u
n,n
u
,nn
u
i,n
a ania , то
есть
[]
1
1000
α
−
⋅⋅⋅=
T
un
a
r
.
Таким образом, матрица
U
A оператора A в базисе ][u имеет вид:
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−−−
=
−− 121
1000
0000
0000
0100
0010
αααα
...
...
...
...............
...
...
...
nnn
U
A . (3.8-15)
Так как
n
ub
r
r
=
, то есть является последним вектором базиса ][u , то ко-
ординатный столбец вектора
b
r
в этом базисе
1] 0 0 ... 0 0 0[=
T
u
b
r
. (3.8-16)
Пара
{
}
UU
b A
r
, называется управляемым каноническим пред-
ставлением (УКП) системы с одним (скалярным) входом. Матрица
U
A
называется сопровождающей по отношению к полиному
)λ(
A
ϕ
.

154
Таким образом, мы доказали, что если исходная система управ-
ляема, то в пространстве состояний Х существует базис, в котором
пара
{
}
bΑ
r
, имеет управляемое каноническое представление.
Если в некотором исходном базисе
][h заданы матрицы
HH
bA
r
, и,
если система управляема, то для того, чтобы вычислить их (матриц)
УКП, достаточно вычислить коэффициенты характеристического поли-
нома
)(
λ
ϕ
A
. После этого может быть вычислена матрица пре-
образования от исходного базиса
][h к УКП в соответствии с (3.7-8):
11 −−
=
HUH
UUU . (3.8-17)
Далее индекс “h” для системы в исходном базисе будем опускать.
ПРИМЕР 3.8-1. Для системы
xCy
ubxAx
r
r
r
&
r
=
+= ;
известны матрицы
[]
11,
2
1
,
54
32
=
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
= CbA
r
.
Нетрудно вычислить матрицу
⎥
⎦
⎤
⎢
⎣
⎡
=≡
142
81
H
UU .
Её определитель 02 ≠−=U , откуда следует, что система управляема
и, значит, для неё существует УКП. Вычислим характеристический по-
лином:
()
{{
21
27
54
32
2
αα
λλ
λ
λ
λλϕ
−−=
⎥
⎦
⎤
⎢
⎣
⎡
−−
−
−
=−=
AE
A
.
Это позволяет сразу же записать матрицы A и B в базисе УКП:
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
1
0
,
72
10
UU
bA
r
.
Векторно-матричные уравнения системы в УКП имеют вид:
.
;
uu
uuuu
xCy
ubxAx
r
r
r
&
r
=
+=
155
Для того, чтобы найти матрицу
U
C , требуется рассчитать матрицу пере-
хода от исходного базиса к базису УКП. Для этого предварительно вы-
числим
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
−
5.01
47
1
H
U и
⎥
⎦
⎤
⎢
⎣
⎡
=
71
10
U
U .
Тогда искомая матрица
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⎥
⎦
⎤
⎢
⎣
⎡
=
−
2/10
2/11
2/11
41
71
10
1
H
U ,
⎥
⎦
⎤
⎢
⎣
⎡
=
20
11
H
U .
После этого в соответствии с (3.6-8) находим
[
]
31 =
=
HHU
CC U .
3.8.2. Передаточная функция и структурная схема для системы в
УКП
Уравнения системы
UU
UUUU
xCy
tubtxAtx
=
+= )()()(
r
r
&
r
(3.8-18)
со скалярным входом
)(tu и скалярным выходом )(t
y
, где матрицы
U
A и
U
b
r
определяются выражениями (3.8-15) и (3.8-16), а матрица
U
C имеет
вид
[
]
unuuU
cccC L
21
= , (3.8-19)
можно записать в развёрнутом виде :
;...
;
... ... ...
;
;
;
112211
1
43
32
21
uxxxxx
xx
xx
xx
xx
nunuununnu
nunu
uu
uu
uu
+−−−−−=
=
=
=
=
−−
−
αααα
&
&
&
&
&
(3.8-20)
nunuuuuu
xcxcxcy
+
+
+
= ...
2211
. (3.8-21)
156
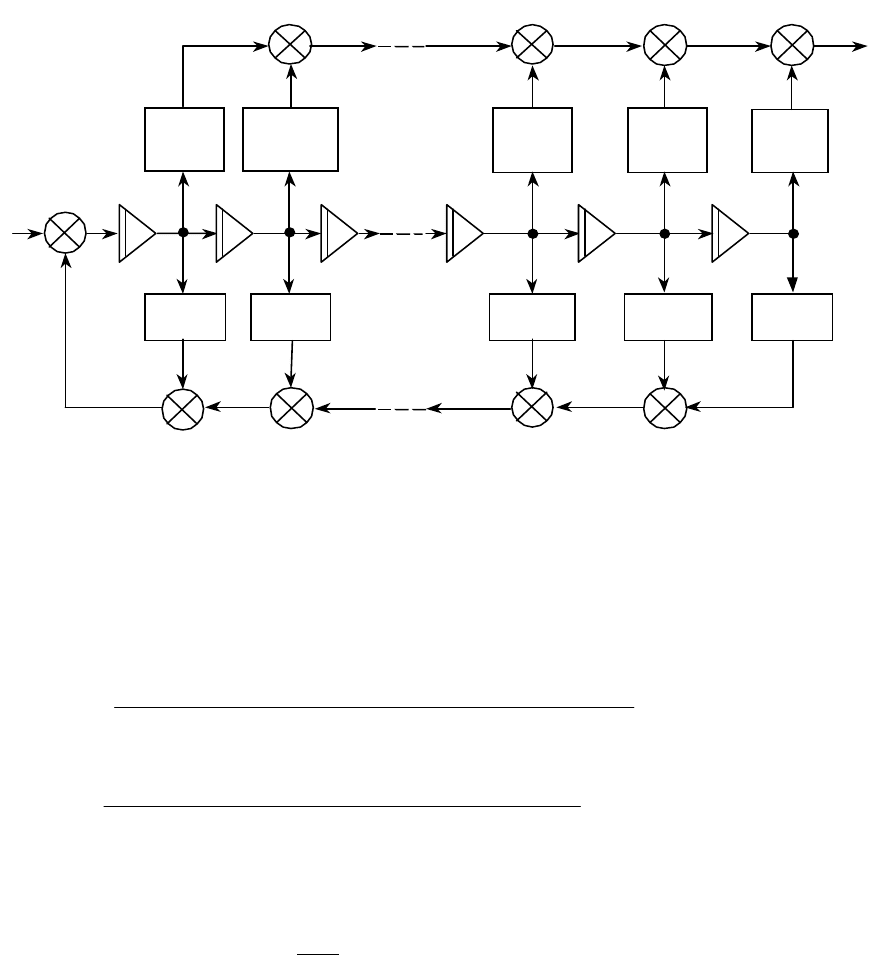
Этим уравнениям соответствует схема, представленная на рис.3.7.
Рис. 3.7. Схема моделирования системы в УКП
u
y
1u
x
2u
x
3u
x
nu
x
1−nu
x
-
α
1
-
α
2
-
α
n-2
-
α
n-1
-
α
n
nu
c
1−nu
c
3u
c
2u
c
1u
c
В соответствии с этим рисунком передаточная функция системы имеет
вид
()
.
...
...
...1
...
)(
1
2
2
1
1
12
121
2
2
1
1
12
1
1
21
nn
nnn
n
nu
n
nuuu
n
n
nunu
n
u
n
u
pppp
pcpcpcc
ppp
pcpcpcpc
pW
αααα
ααα
+++++
++++
=
=
++++
+
+
+
+
=
−
−−
−−
−
−−−
−−
−
−−−
(3.8-22)
Отметим, что статический передаточный коэффициент
n
u
c
W
α
1
)0( = . (3.8-23)
3.8.3. Идентификационное каноническое представление системы с
одним (скалярным) выходом
С помощью рассуждений, аналогичных проведённым в п.3.8.1,
можно получить следующие результаты.
Если пара матриц
{}
CA, полностью наблюдаема, то в простра-
нстве состояний Х всегда существует базис, в котором пара
{
}
CA,
имеет идентификационное каноническое представление (ИКП):
157
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
−
=
−
−
1
2
3
2
1
10...00
01...00
00...00
..................
00...10
00...01
00...00
α
α
α
α
α
α
n
n
n
I
A ; (3.8-24)
[]
100...00=
I
C . (3.8-25)
Отметим, что:
U
T
IU
T
I
bCAA
r
== ; . (3.8-26)
Если в некотором исходном базисе
][h заданы матрицы
HH
A C , и, если система полностью наблюдаема, то для того, чтобы
вычислить их (матриц) ИКП, достаточно вычислить коэффициенты ха-
рактеристического полинома
)(
λ
ϕ
A
. После этого может быть вычислена
матрица преобразования от исходного базиса
][h к ИКП в соответствии
с (3.7-13):
IHH
NN
11 −−
=I . (3.8-27)
Если известна матрица
H
B при векторе управления в исходном ба-
зисе, то с учётом (3.6-8) в базисе ИКП она может быть определена с
помощью соотношения
HHI
BB
1−
= I . (3.8-28)
3.8.4. Передаточная функция и структура для системы в ИКП
В соответствии с видом матриц
I
A и
I
C уравнения системы со ска-
лярным входом
u
и скалярным выходом
y
имеют вид:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+−=
+−=
+−=
+−=
+
−
=
−
−−−
−
−
;
;
... ... ... ... ... ...
;
;
;
11
1221
3223
2112
11
ubxxx
ubxxx
ubxxx
ubxxx
ubxx
nininini
nininini
ininii
ininii
inini
α
α
α
α
α
&
&
&
&
&
(3.8-29)
158
ni
xy = . (3.8-30)
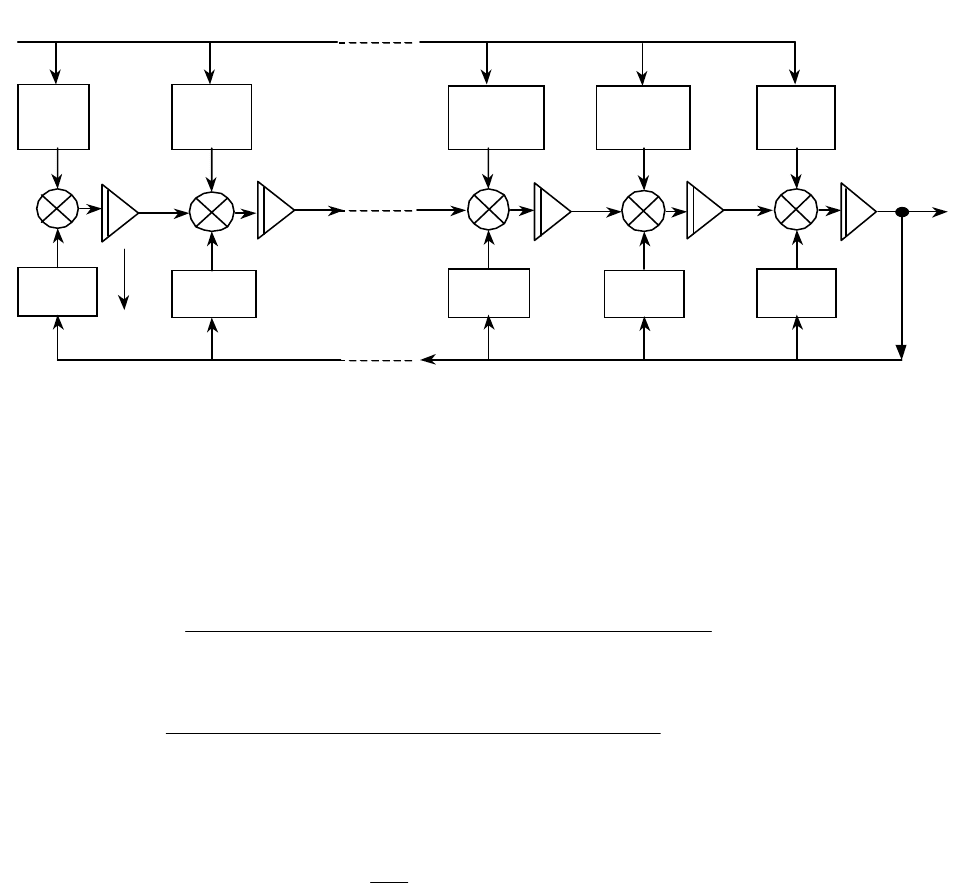
Этим уравнениям соответствует структурная схема, представленная на
рис. 3.8.
-
α
1
-
α
2
-
α
3
-
α
n-1
-
α
n
Рис. 3.8. Схема моделирования системы в ИКП
u
y
ni
x
1−ni
x
ni
b
2−ni
x
1−ni
b
2i
x
2−ni
b
1i
x
2i
b
1i
b
В соответствии с этим рисунком передаточная функция системы имеет
вид:
()
.
...
...
...1
...
)(
1
2
2
1
1
12
121
2
2
1
1
12
1
1
21
nn
nnn
n
ni
n
niii
n
n
nini
n
i
n
i
pppp
pbpbpbb
ppp
pbpbpbpb
pW
αααα
ααα
+++++
++++
=
=
++++
++++
=
−
−−
−−
−
−−−
−−
−
−−−
(3.8-31)
Отметим, что статический передаточный коэффициент
n
i
b
W
α
1
)0( = . (3.8-32)
159
3.9. Обратная связь по состоянию, обеспечивающая задан-
ное (желаемое) расположение собственных чисел в
замкнутой системе с одним (скалярным) входом
Даны уравнения полностью управляемого объекта управления в
некотором исходном базисе
,)(
);()()(
HH
HHH
xCty
tubtxAtx
r
r
r
&
r
=
+=
(3.9-1)
каждая координата вектора состояния которого доступна для измерения.
Требуется синтезировать такое управление, которое бы обеспечило
требуемое качество отработки внешнего командного сигнала
)(tv .
Динамические свойства системы управления, в основном, опреде-
ляются её собственными числами, то есть нулями характеристического
полинома
()
()
n
nn
n
i
iA
αλαλλλλϕ
+++=−=
−
=
∏
...
1
1
1
. (3.9-2)
Время переходного процесса каждой моды определяется расстоя-
нием до мнимой оси вещественной части; колебательность - соотноше-
нием мнимой и вещественной частей соответствующих собственных чи-
сел. Эти зависимости могут быть проанализированы при изучении ха-
рактеристик типовых звеньев, кроме того, они рассматриваются в об-
ширной учебной литературе по теории автоматического регулирования и
управления
.
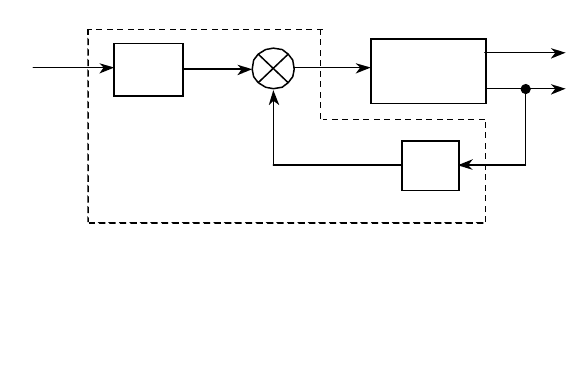
В соответствии со структурной схемой, приведённой на рис. 3.9,
сформируем сигнал управления объектом в виде:
)()()( tvktxLtu
v
HH
+
=
r
, (3.9-3)
где:
H
L – некоторая матрица-строка обратной связи:
[
]
nhhhH
lllL ...
21
= ; (3.9-4)
v
k – коэффициент по командному сигналу.
Тогда уравнение системы примет вид:
)()()()( tvkbtxLbtxAtx
v
HHHHHHH
r
r
r
r
&
r
++=
, (3.9-5)
или
)()()( tvkbtxAtx
v
HH
C
HH
r
r
&
r
+=
, (3.9-6)
где
C
H
A - матрица замкнутой системы в исходном базисе:
HHH
C
H
LbAA
r
+= . (3.9-7)
160
Рис. 3.9. Структурная схема замкнутой
системы
v
y
x
r
u
Регулятор
Объект
v
k
L
Поскольку объект полностью управляем, то существует базис ][u ,
в котором пара
{
}
bA
r
, имеет управляемое каноническое представление
{
}
UU
bA
r
, . Поэтому перейдём к записи уравнений системы в базисе УКП.
В соответствии с (3.4-16) произведём замену
UHH
xx
r
r
U= . (3.9-8)
Тогда из (3.9-1) получим
)()()( tubtxAtx
HUHHUH
r
r
&
r
+= UU
; (3.9-9)
UHH
xCty
r
U=)(
. (3.9-10)
Умножив уравнение (3.9-9) слева на
1−
H
U , будем иметь
,)()(
;)()()(
txCty
tubtxAtx
UU
UUUU
r
r
r
&
r
=
+=
, (3.9-11)
где
U
A
U
b
r
и
U
C - соответствующие матрицы в УКП.
Используя подстановку (3.9-8), из (3.9-3) получим
)()( tvkxLtu
v
UU
+=
r
, (3.9-12)
где матрица обратной связи в базисе УКП
HHU
LL U= . (3.9-13)
В результате, уравнение замкнутой системы в базисе управляе-
мого канонического представления будет иметь вид:
)()()( tvkbtxAtx
v
UU
C
UU
⋅+=
r
r
&
r
. (3.9-14)
Здесь
C
U
A является сопровождающей матрицей по отношению к харак-
теристическому полиному замкнутой системы
