Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

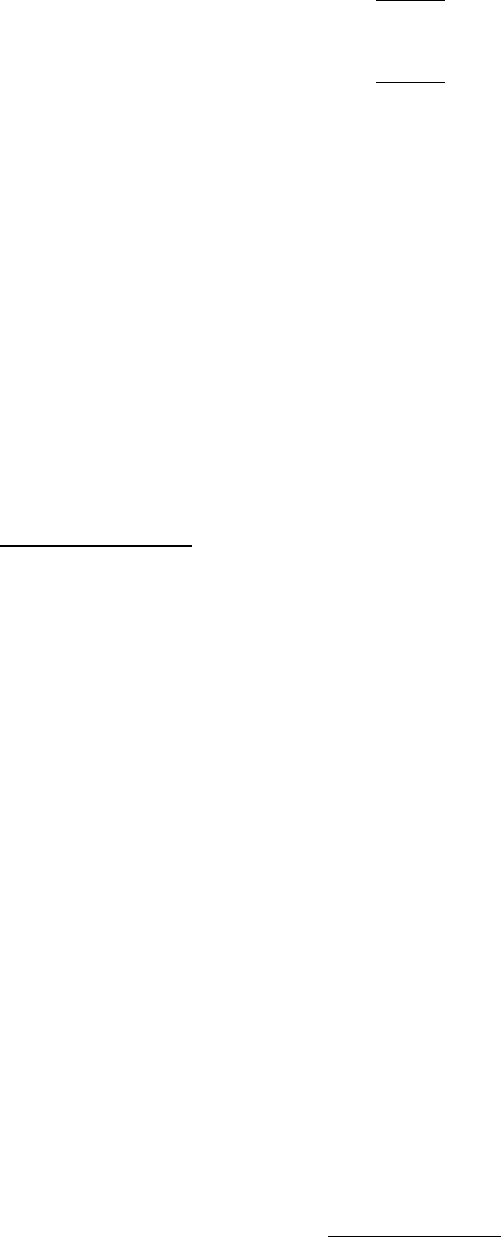
131
у неё только один, устойчивый полюс и по ней не видно, что в действи-
тельности система неустойчива.
Матричная передаточная функция по вектору состояния
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
−
=
7
3
7
5
)(
p
p
pW
ux
.
Ей соответствует решение дифференциального уравнения системы
∫
−−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
+=
t
tAt
duexetx
0
)(7
)(
3
5
)0()(
ττ
τ
rr
.
Как видно, в вынужденной составляющей решения отсутствует одна -
неустойчивая - мода. Кроме того, независимо от управляющего сигнала
для координат вынужденной составляющей вектора состояния сущест-
вует линейная связь
)(6.0)(
12
txtx
ВВ
−= .
ПРИМЕР 3.2-2
. Определить управляемость системы
.
;323
;1054
1
212
211
xy
Uxxx
Uxxx
=
+−=
−
+
−
=
&
&
Для этой системы
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
3
10
,
23
54
BA
и матрица управляемости
[]
⎥
⎦
⎤
⎢
⎣
⎡
−
−
==
363
2510
ABAU .
Определитель этой матрицы не равен нулю, она имеет ранг, равный
двум, то есть порядку системы, и система является полностью управ-
ляемой.
Отметим, что в данном случае полюсы передаточной функции
)7)(1(
)1(10
)(
+−
+
−=
pp
p
pW
uy
полностью повторяют все собственные числа матрицы
A
.
132
3.3. Наблюдаемость линейных стационарных систем.
В теории автоматического управления большую роль играет зада-
ча восстановления вектора состояния по результатам наблюдения за
входом и выходом объекта.
Непрерывная система
)()(
)()()(
txCty
tuBtxAtx
vv
v
v
&
v
=
+=
(3.3-1)
называется наблюдаемой, если вектор состояния
)(
0
tx
v
можно опреде-
лить, зная
)(ty
r
на некотором интервале времени ],[
10
ttt
=
. Если это
справедливо для любого
0
t , то система называется полностью наблю-
даемой. Задачей настоящего параграфа является вывод критерия на-
блюдаемости.
Достаточно рассмотреть задачу при
0)(
=
tu
r
. Тогда
)0()( xCety
At
r
r
= . (3.3-2)
В развёрнутом виде - это система алгебраических уравнений
)(...
)(...
)(...
,1
112222121
111212111
nnynnnyny
nn
nn
tyxCxC
tyxCxCxC
tyxCxCxC
=++
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
=+++
=
+++
, (3.3-3)
в качестве неизвестных в которой выступают координаты вектора со-
стояния. В связи с тем, что, как правило,
nn
y
<
, число уравнений ока-
зывается меньше числа неизвестных, и решение невозможно.
В соответствии с теоремой Кэли-Гамильтона каждая квадратная
матрица удовлетворяет собственному характеристическому уравнению:
0...
1
1
1
=
+
+++
−
−
EAAA
nn
nn
α
α
α
. (3.3-5)
Поэтому матричная экспонента, являющаяся степенным рядом относи-
тельно матрицы
A
, может быть представлена в виде полинома степени
1−n . С учетом этого равенство (3.3-2) можно записать в виде:
133
∑
−
=
⋅⋅=
1
0
)0()()(
n
l
l
l
xACtty
r
r
γ
, (3.3-5)
где
)(t
l
γ
– соответствующие коэффициенты этого полинома. Для i-й со-
ставляющей вектора выхода соответственно будем иметь
∑
−
=
=
1
0
)0())(()(
n
l
i
l
li
xCAtty
v
v
γ
. (3.3-6)
Здесь
i
l
CA )( – i -я строка матрицы )(
l
CA .
Если набор
i
l
CA )( для
y
ni ,...,2,1= ; 1,...,2,1,0
−
=
n
l
не содержит пол-
ного базиса, то есть
n линейно независимых строк, иначе говоря, если
матрица
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
−1
2
...
n
CA
CA
CA
C
N
(3.3-7)
имеет ранг, меньший, чем
n , то в качестве ненулевого вектора началь-
ных условий
0)0( ≠x
r
может быть выбран вектор, ортогональный всем
строкам матрицы N. Тогда в соответствии с (3.3-5) получим, что
0)( =ty
r
для всех
t
, т.е. система не наблюдаема.
Теперь докажем, что если ранг матрицы N равен
n , то )(
0
tx
r
может
быть определен с помощью конечного числа измерений вектора выхода
)(ty
v
. Обозначим
[]
EtEtEtt
knkkk
)( ... )( )()(
110 −
=Γ
γ
γ
γ
, (3.3-8)
где Е – квадратная единичная матрица размером
][
yy
nn ×
. Моменты
измерения
k
t выберем таким образом, чтобы для различных значений k
элементы
)(
ki
t
γ
отличались друг от друга. С учетом введенного обозна-
чения равенство (3.3-5) примет вид
)0()()( xNtty
kk
r
r
Γ=
. (3.3-9)
Известно, что ранг произведения любых двух матриц не превосхо-
дит ранга каждого из сомножителей. Ранг матрицы
)(
k
t
Γ
не превосхо-
дит числа ее строк
nn
y
< . Проводя многократные измерения на интер-
вале времени переходного процесса системы, построим расширенный
вектор выхода

134
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
)(
...
)(
)(
2
1
n
R
ty
ty
ty
Y
r
r
r
r
(3.3-10)
и обозначим
()
()
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
Γ
Γ
=Γ
n
R
t
t
...
1
. (3.3-11)
Матрица
Γ имеет
nn
y
×
строк. Моменты измерений должны быть
выбраны таким образом, чтобы выполнялось условие
nrank
R
=Γ . Как
было обусловлено, ранг матрицы
N
также равен n . Поэтому уравнение
RR
YxN
r
r
=⋅⋅Γ )0(
(3.3-13)
содержит
n линейно независимых скалярных уравнений, то есть оно
может быть разрешено относительно вектора
)0(
x
v
.
Таким образом, доказан следующий
критерий полной наблю-
даемости стационарных линейных систем
:
Линейная стационарная система вполне наблюдаема тогда и только то-
гда, когда ранг матрицы наблюдаемости N равен
n .
ПРИМЕР 3.3-1
. . Объект управления задан уравнениями
.2
;24
;338
21
212
211
xxy
uxxx
uxxx
−=
+−−=
+
+−=
&
&
Этим уравнениям соответствуют матрицы
[]
21;
2
3
;
41
38
−=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−−
−
= CBA
.
Определитель матрицы управляемости
⎥
⎦
⎤
⎢
⎣
⎡
−
=
32
153
U
не равен нулю, поэтому система управляема. Матрица наблюдаемости
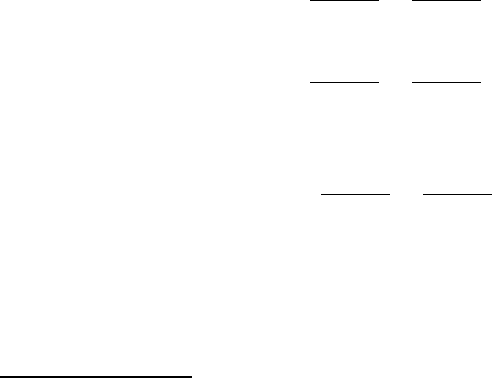
135
⎥
⎦
⎤
⎢
⎣
⎡
−−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
56
21
CA
C
N
Её определитель также отличен от нуля, следовательно, система
полностью наблюдаема.
Для данного объекта нетрудно рассчитать собственные числа
7;5
21
−
=
−
=
λ
λ
,
правые
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
1
3
;
1
1
21
vv
rr
и левые
[]
5.15.0
1
−=
T
d
r
;
[
]
5.05.0
2
−=
T
d
r
собственные векторы.
В соответствии с (2.4-27), (2.6-4) и (2.6-6) нетрудно получить пере-
даточные функции по векторам состояния и выхода:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
+
+
+
+
+
+
=
7
5.0
5
5.1
7
5.1
5
5.1
)(
pp
pp
pW
x
;
7
5.0
5
5.1
)(
+
+
+
−=
pp
pW
y
.
В данном случае полюсы передаточной функции по выходу полностью
отображают собственные числа матрицы динамики.
ПРИМЕР 3.3-2
. . Объект управления задан уравнениями
uxxx
uxxx
24
338
212
211
+−−=
++−=
&
&
;
21
3xxy
−
=
.
Матрицы
A
и B здесь такие же, как и в предыдущем примере, следова-
тельно, объект управляем. Матрица выхода
[]
31
−
=C .
Ранг матрицы наблюдаемости
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
⎥
⎦
⎤
⎢
⎣
⎡
=
155
31
CA
C
N

136
в данном случае меньше порядка объекта и равен единице, так как вто-
рой столбец пропорционален первому. Следовательно, данный объект
неуправляем.
Правые и левые собственные векторы матрицы динамики и пере-
даточная функция по вектору состояния такие же, как и в предыдущем
примере. Передаточная функция по выходу
5
3
)(
+
−=
p
pW
y
.
У неё отсутствует полюс, равный второму собственному числу матрицы
A
.
Определим свободное движение объекта по вектору состояния и
по выходу:
.)()(
;)0()0()(
2
1
txCty
xdvexetx
i
T
ii
t
At
i
r
r
r
r
rr
=
==
∑
=
λ
.
Получаем:
tt
exextx
75
)0(
5.05.0
5.15.1
)0(
5.15.0
5.15.0
)(
−−
⎥
⎦
⎤
⎢
⎣
⎡
−
−
+
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
rrr
;
[]
t
exty
5
)0(31)(
−
−
=
r
.
Если выбрать
⎥
⎦
⎤
⎢
⎣
⎡
==
1
3
)0(
2
vx
rr
,
то так как векторы
2
v
r
и
1
d
r
взаимно ортогональны, и их скалярное произ-
ведение равно нулю, получим
t
etx
7
1
3
)(
−
⎥
⎦
⎤
⎢
⎣
⎡
=
r
,
в то время как
0)( =ty
r
.

137
3.4. Замена базиса в линейном конечномерном пространст-
ве
Линейное пространство R называется конечномерным, а число n –
числом измерений этого пространства или его размерностью
(
ndimR = ), если в R существует n линейно независимых векторов, в то
время как любые
1+n векторов в
R
линейно зависимы.
Система из
n линейно независимых, заданных в определенном
порядке векторов
n
eee
rrr
,...,,
21
в n -мерном пространстве называется ба-
зисом этого пространства.
Если каждый из векторов базиса ортогонален любому другому век-
тору этого базиса, т.е. их скалярные произведения равны нулю, то такой
базис называется ортогональным
. Если, кроме того, модуль каждого
вектора базиса равен единице, то базис называется ортонормирован-
ным.
Векторы
n
eeex
rrr
r
,...,,,
21
, где
x
r
- любой вектор из
R
, линейно зави-
симы, так как их
1
+
n . Отсюда справедливо равенство:
0...
22110
=
+
+++
nn
eeex
r
r
r
r
α
α
α
α
, (3.4-1)
откуда
nenee
exexexx
r
r
r
r
+
+
+= ...
2211
. (3.4-2)
Здесь:
enee
xxx ,...,,
21
- координаты вектора
x
r
в базисе }{e .
Столбец
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
en
e
e
e
x
x
x
x
...
2
1
r
(3.4-3)
называют координатным столбцом вектора
x
r
в этом базисе.
x
r
- вектор в пространстве, и только если в этом пространстве вы-
берем базис, то возникает понятие координатного вектор-столбца
e
x
r
.
Если установим другой базис, то ему будет соответствовать другой ко-
ординатный вектор-столбец.
Пусть в
n -мерном пространстве задано два базиса:
n
eeee
r
rr
,...,,:}{
21
и
138
n
ffff
r
rr
,...,,:}{
21
.
Так как это векторы одного и того же пространства, то каждый из векто-
ров базиса
}{f можно разложить через векторы базиса }{e :
....
;...
;...
2211
22221122
12211111
nennnenen
nenee
nenee
efefeff
efefeff
efefeff
rrr
r
rrr
r
r
r
r
r
+++=
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
+++=
+++=
(3.4-4)
Коэффициенты
eik
f (здесь i –номер координаты, а k –номер расклады-
ваемого вектора) можно представить в виде квадратной матрицы
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
nn en2 en1 e
e2ne22e21
e1ne12e11
f...ff
....................
f...ff
f...ff
e
F
, (3.4-5)
или
[
]
ene2e1
fff
r
rr
⋅⋅⋅=
e
F . (3.4-6)
Каждый из столбцов матрицы
e
F – это координатные столбцы векторов
n
fff
rrr
,...,,
21
базиса }{f в базисе }{e .
С учетом введенных обозначений систему равенств (3.4-4) можно
записать в виде
[]
[
]
[]
[]
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
⋅=
⋅=
⋅=⋅=
n
en
e
een
fef
fef
fefeeef
rr
rr
r
r
r
r
r
r
..................................................
...
2
11
2
211
. (3.4-7)
Можно ещё более упростить (укрупнить) эти равенства, используя поня-
тия блочных матриц:
[
]
[
]
eneen
fefefefff
r
r
r
r
rr
⋅⋅⋅⋅⋅⋅=⋅⋅⋅ ][][][
2121
(3.4-8)
или, в итоге
[] []
e
Fef =
. (3.4-9)
139
Матрица
e
F называется матрицей перехода от базиса }{e к бази-
су
}{f . Так как
e
F невырожденная, то
[] []
f
fe E⋅=
, (3.4-10)
где матрица
-1
ef
FE = (3.4-11)
называется матрицей перехода от базиса
}{f к базису }{e .
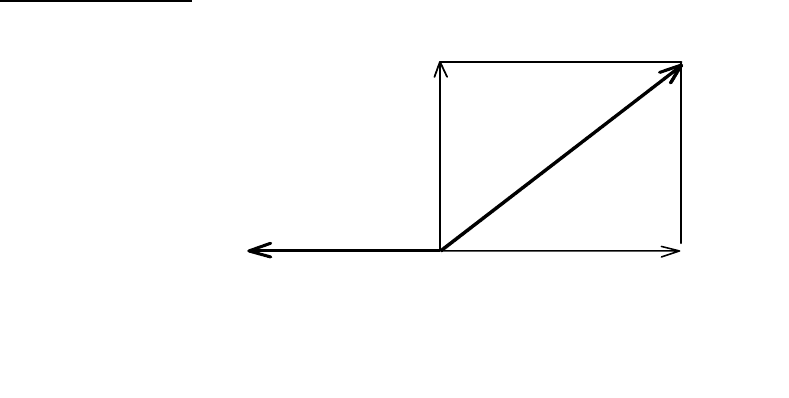
ПРИМЕР 3.4-1
. Пусть в R
2
задан базис }{e векторами
21
,ee
r
r
(рис. 3.3).
2
e
r
1
f
r
1
e
r
2
f
r
Рис. 3.3. Связь между векторами
различных базисов
Введем базис }{f следующим образом:
.01
;11
212
211
eef
eef
rr
r
r
r
r
⋅+⋅−=
⋅+⋅=
Запишем матрицу перехода от базиса
}{e к базису }{f :
⎥
⎦
⎤
⎢
⎣
⎡
−
=
01
11
e
F
.
Найдем обратную матрицу
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
11
10
1
e
F
и, в соответствии с (3.4-10), получаем
[]
[]
[
]
2122121
fff
11
10
ffee
r
r
r
r
r
rr
+−=
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅=
.
Этот результат подтверждается анализом рис. 3.3.
140
Рассмотрим, как связаны между собой компоненты, (координатные
столбцы) одного и того вектора
x
r
в разных базисах. В соответствии с
(3.4-2)
nenee
exexexx
r
r
r
r
+
+
+= ...
2211
(3.4-12)
и
nfnff
fxfxfxx
r
rr
r
+++= ...
2211
. (3.4-13)
Приравнивая правые части последних двух равенств, получим
[
][]
fe
xfxe
r
r
⋅
=⋅ , (3.4-14)
а с учётом (3.4-9)
[]
fee
xex
r
r
F=][e (3.4-15)
Окончательно получаем
;
fee
xx
r
r
F=
e
xx
1
ef
r
r
⋅
=
−
F . (3.4-16)
3.5. Линейные операторы и матрицы линейных операторов.
Отображение
A
линейного пространства
X
в линейное пространство
Y
Y
X
→:
A
называют линейным преобразованием или линейным оператором, если
оно удовлетворяет двум условиям:
а)
)()()( vxvx
r
rrr
AAA +=+ для всех Xvx
∈
r
r
, ; (3.5-1)
б)
)()( xx
rr
AA
α
α
= для всех
Xvx
∈
r
r
и любого
α
. (3.5-2)
Если отображение
A
переводит вектор
x
r
в некоторый другой век-
тор
y
r
:
()
yx
r
r
=A , (3.5-3)
то вектор
y
r
- называют образом вектора
x
r
, а
x
r
- прообразом вектора y
r
.
Линейный оператор, отображающий линейное пространство
n
R
само в себя, называется линейным оператором в
n
R
.
