Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

141
Пусть
nn
RyRx ∈∈
rr
; и )(xy
r
r
A
=
. Рассмотрим, как связаны в
этом случае координаты векторов
x
r
и y
r
. Будем ориентироваться сна-
чала на базис
[]
n
eeee
r
rr
⋅
⋅
⋅
=
21
][ . Очевидно при этом, что
∑
=
=
n
k
kek
exx
1
r
r
; (3.5-4)
∑
=
=
n
i
iei
eyy
1
r
r
. (3.5-5)
Рассмотрим, прежде всего, как действует оператор
A
на элемен-
ты базиса. Пусть
()
()
()
n
e
nn
e
n
e
nn
n
e
nk
e
k
e
kk
n
e
n
ee
eaeaeae
eaeaeae
eaeaeae
rrrr
rrrr
r
rrr
+++=
+++=
+
+
+=
...
.................................................
...
................................................
...
2211
2211
12211111
A
A
A
(3.5-6)
Из соотношений (3.5-3) и (3.5-4) следует
()
∑
=
=
n
k
ke
exy
k
1
r
r
A
. (3.5-7)
Учтём (3.5-6):
∑∑
==
=
n
k
n
i
i
e
ikek
eaxy
11
r
r
. (3.5-8)
Сопоставляя это равенство с (3.5-5), получим
nixay
n
k
ek
e
ikei
,...,2,1 ,
1
==
∑
=
r
(3.5-9)
Запишем этот результат в матричной форме:
eee
xAy
r
r
⋅=
, (3.5-10)
где, как и раньше
e
y
r
и
e
x
r
- координатные вектор-столбцы, соответст-
вующих векторов в базисе
][e , а матрица

142
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
e
nn
e
n
e
n
e
n
ee
e
n
ee
e
aaa
aaa
aaa
A
...
....................
...
...
21
22221
11211
(3.5-11)
называется матрицей оператора
A
в базисе ][e . Элементы её столб-
цов по построению - это координаты векторов
(
)()
.....,
21
ee
r
r
AA
базисе
][e . Аналогично вводится понятие матрицы
f
A того же операто-
ра
A
в некотором другом базисе ][f .
Рассмотрим теперь, как изменяется матрица оператора
A
при
замене базиса в пространстве
n
R
. Пусть, как и прежде
(
)
xy
r
r
A=
и
матрица
e
A , в соответствии с (3.5-10) связывает между собой коорди-
натные столбцы векторов
x
r
и y
r
в базисе ][e .
Согласно ранее полученным результатам - соотношениям (3.4-16),
fee
xx
r
r
⋅= F
(3.5-12)
и
fee
yy
r
r
⋅= F
. (3.5-13)
Из этих двух соотношений и (3.5-10) легко выводится равенство
fff
xAy
r
r
⋅=
, (3.5-14)
где
eeef
AA FF
⋅
⋅=
−1
. (3.5-15)
Эта формула позволяет связать между собой матрицы одного и то-
го же оператора в различных базисах. В математике такие матрицы на-
зываются подобными. Ранее (п.2.4.3) уже отмечалось, что подобные
матрицы имеют одинаковые собственные числа.
ПРИМЕР 3.4-2
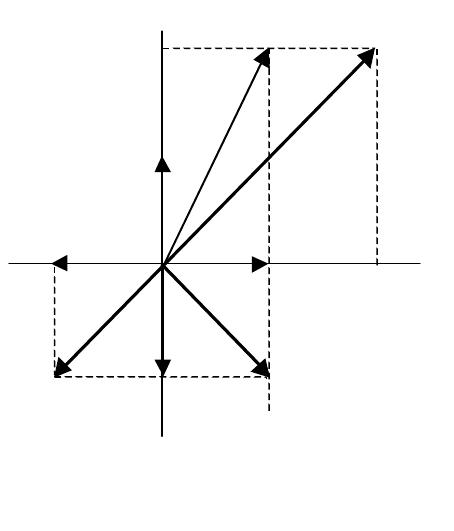
. Пусть имеется базис ][e (рис. 3.4)
1. Зададим оператора
A
его действием на векторы базиса ][e :
()
()
.
;2
12
211
ee
eee
rr
r
rr
−=
+=
A
A
Тем самым мы определили матрицу оператора
A в базисе ][e :
⎥
⎦
⎤
⎢
⎣
⎡
−
=
02
11
e
A .
143
2. Зададим вектор
x
r
в базисе ][e :
21
eex
r
r
r
−= .
Рис. 3.4. Действие оператора
на векто
р
1
e
r
y
r
2
e
r
)(
1
eA
r
x
r
)
(
2
eA
r
1
f
r
2
f
r
Отсюда
⎥
⎦
⎤
⎢
⎣
⎡
−
=
1
1
e
x
r
.
3. Рассчитаем координатный вектор, используя (3.5-14):
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
==
2
2
1
1
02
11
eee
xAy
rr
.
4. Введем новый базис
][f :
.
;
212
21
eef
ef
rr
r
r
r
−−=
−=
Тогда матрица перехода от базиса
][e к базису ][f будет иметь вид
⎥
⎦
⎤
⎢
⎣
⎡
−−
−
=
11
10
e
F .
5. Определим матрицу
f
A оператора A в базисе ][f :
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−−
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
⋅
⎥
⎦
⎤
⎢
⎣
⎡
−
−
==
−
01
21
11
10
02
11
01
11
1
eeef
AA FF .

144
6. Найдём координатный столбец вектора
x
r
в базисе ][f . В соответст-
вии с рис. 3.4
21
2 ffx
r
r
r
−=
.
С другой стороны, согласно (3.5-12)
eef
xx
r
r
⋅=
−1
F . (3.5-16)
Оба подхода дают один и тот же результат:
⎥
⎦
⎤
⎢
⎣
⎡
−
=
1
2
f
x
r
.
В итоге получим координатный столбец вектора
y
r
в базисе ][f :
⎥
⎦
⎤
⎢
⎣
⎡
−
==
2
0
fff
xAy
rr
.
ПРИМЕР 3.5-1
. Дана матрица
e
A оператора A в базисе ][e :
⎥
⎦
⎤
⎢
⎣
⎡
=
00
10
e
A
и два вектора -
1
f
r
и
2
f
r
, координатные столбцы которых в том же базисе
имеют вид:
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
1e
f
r
;
⎥
⎦
⎤
⎢
⎣
⎡
=
3
0
2e
f
r
,
то есть
.3
;2
22
211
ef
eef
r
r
r
r
r
=
+=
Примем эти векторы в качестве нового базиса и вычислим в нём матри-
цу
f
A оператора A . Для этого выполним следующие действия.
1. Составим матрицу перехода от базиса
][e к базису ][f :
⎥
⎦
⎤
⎢
⎣
⎡
=
32
01
e
F .
2. Вычислим обратную матрицу:

145
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−
=
−
3
1
3
2
01
1
e
F .
3. Вычислим матрицу
f
A :
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
=⋅⋅=
−
2
3
4
32
1
eeef
AA FF .
3.6. Замена базиса в пространстве состояний динамиче-
ской системы
Пусть заданы уравнения системы
.)()(
;)()(
txCty
tuBtxAx
rr
r
rr
=
+=
(3.6-1)
Для этой системы могут быть найдены матрицы управляемости
[]
BABAABBU
n 12
...
−
= , (3.6-2)
наблюдаемости
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−1
...
n
CA
CA
C
N
, (3.6-3)
передаточной функции
BApECpW
y
1
)()(
−
−
= . (3.6-4)
Могут быть также записаны выражения для векторов состояния и выхо-
да
∫
∫
−Φ+−Φ=
−Φ+−Φ=
t
t
t
t
duBtCtxttCty
duBttxtttx
0
0
.)()()()()(
;)()()()()(
00
00
τττ
τττ
rrr
rrr
(3.6-5)
Полученные в предыдущих разделах результаты не были ограни-
чены выбором какого-либо конкретного базиса в пространстве состоя-

146
ний. Все они были справедливы для любого базиса, в котором записаны
матрицы
NUWФCB
A
,,,,,, . Для определённости назовём этот ба-
зис базисом
][e . В этом случае можно подразумевать, что символы
всех векторов и матриц в выражениях (3.6-1) - (3.6-5) снабжены индек-
сом "
e ". В дальнейшем нам будет удобно выбирать вполне опреде-
ленный базис в пространстве состояний
X
таким образом, чтобы мат-
рицы имели «хорошую», каноническую форму. Такой выбор базиса мо-
жет оказаться целесообразным, так как, во-первых, канонические пред-
ставления матриц системы имеют минимальное число ненулевых эле-
ментов и поэтому удобны для моделирования и других вычислений, а
во-вторых, канонические представления позволяют получить чрезвы-
чайно простые алгоритмы
синтеза управления.
Рассмотрим перевод уравнений (3.6-1) в некоторый новый базис
F . Отметим при этом, что, переходя к новому базису в пространстве
состояний, преобразовывая базис для пространства вектора состояний,
не будем изменять базис пространства входов и пространства выходов
системы. Заменим в (3.6-1)
e
x
r
на
f
x
r
согласно (3.5-12):
.
;
fee
efeefe
xCy
uBxAx
rr
r
r
&
r
F
FF
=
+⋅=⋅
(3.6-6)
Умножая слева обе части дифференциального уравнения на
1−
F , полу-
чим:
uBxAx
eefeeef
r
r
&
r
11 −−
+= FFF
. (3.6-7)
Учитывая (3.5-15), и вводя дополнительные обозначения
,
;
;
1
1
eef
eef
eeef
CC
BB
AA
F
F
FF
⋅=
⋅=
⋅
⋅=
−
−
(3.6-8)
окончательно получаем уравнения системы в базисе
][f :
()
() ()
.
;
txCty
tuBAx
f
fff
r
&
r
r
&
r
⋅=
⋅+=
(3.6-9)
ПРИМЕР 3.6-1
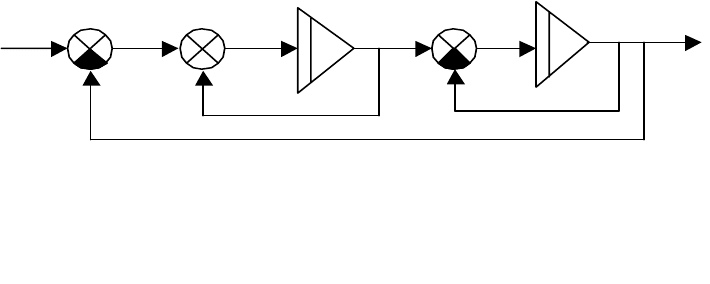
. Пусть система задана схемой моделирования, приве-
денной на рис. 3.5. Выберем в качестве координат вектора состояний
x
r
в исходном базисе
][e выходы интеграторов 1 и 2. В результате полу-
чим уравнения системы в исходном базисе:
147
,)()(
;)()()(
txCty
tuBtxAtx
ee
eeee
rr
r
r
&
r
⋅=
⋅+=
Рис. 3.5. Схема моделирования в исходном
базисе
][e
u
1e
x
2e
x
y
1
2
где
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
11
11
e
A
;
⎥
⎦
⎤
⎢
⎣
⎡
=
0
1
e
B
;
[
]
10
=
e
C .
Зададим матрицу перехода к новому базису:
⎥
⎦
⎤
⎢
⎣
⎡
=
01
11
e
F ,
которой соответствуют уравнения
.
;
12
211
ef
eef
=
+=
r
r
r
r
Вычислим обратную матрицу
⎥
⎦
⎤
⎢
⎣
⎡
−
=
−
11
10
1
e
F .
В соответствии с (3.6-8) находим
⎥
⎦
⎤
⎢
⎣
⎡
=
00
10
f
A ; ;
1
0
⎥
⎦
⎤
⎢
⎣
⎡
=
f
B
[
]
01
=
f
C .
Этим матрицам соответствуют уравнения
,
;
;
1
2
21
f
f
ff
xy
ux
xx
=
=
=
&
&
148
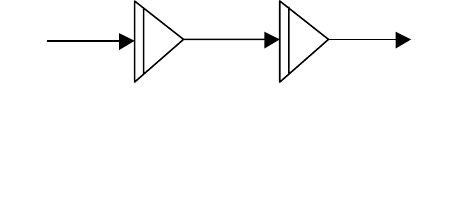
которым, в свою очередь, отвечает схема, приведённая на рис. 3.6.
u
2f
x
1f
x
y
Рис. 3.6. Схема
моделирования в базисе
][f
Собственные числа системы, естественно, сохранились, так как
матрицы
l
А
и
f
A
подобны. Связь между входом и выходом осталась
неизменной, а схема моделирования стала заметно проще.
3.7. Вычисление матрицы преобразования базиса в про-
странстве состояний динамической системы с помо-
щью матриц управляемости и наблюдаемости
Пусть матрицы управляемой системы представлены в двух раз-
личных базисах
][e и ][f в пространстве состояний вектора
x
r
:
{
}
{
}
ffee
B,A,B,A .
Рассмотрим матрицу управляемости:
[]
f
1n
ff
2
fffff
BA...BABAB
−
=U . (3.7-1)
В соответствии с (3.6.-8)
eeeff
BABA
1
−
= F :
eeeeeeeeeeeff
BABAABA
211112 −−−−
=
= FFFFFF ;
………….
e
k
ee
k
f
BAA
1−
= F . (3.7-2)
Учитывая эти равенства в (3.7-1), получим выражение для перевода
матрицы управляемости из одного базиса в другой:
eef
UU
1−
= F . (3.7-3)
Умножая это равенство справа на
T
e
U , получаем:
T
eee
T
ef
UUUU
1−
= F . (3.7-4)
Если система управляема, то nUrankUrank
fe
=
=
. Это значит,
что матрица
e
U имеет n линейно независимых строк и может быть
представлена в виде

149
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
T
n
T
T
e
z
z
z
U
r
r
r
...
2
1
, (3.7-5)
где векторы
n
zzz
rrr
...,
21
– линейно независимы. Следовательно, матрица
[]
n
T
n
T
T
T
ee
zzz
z
z
z
UU
rrr
r
r
r
...
...
21
2
1
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
, (3.7-6)
которая является матрицей Грама, имеет положительный определитель,
а значит – невырождена
. Следовательно,
11
)(
−−
=
T
ee
T
efe
UUUUF . (3.7-7)
Если система имеет скалярный вход (u-скаляр), то матрица
B ста-
новится вектором
)( bB
r
= , а матрица
e
U – квадратной, в управляемой
системе – невырожденной. Тогда:
11 −−
=
efe
UUF
. (3.7-8)
Отметим, что в данном рассуждении
e
F – матрица перехода от базиса
][e к базису ][f , поэтому обратная ей - это матрица перехода от базиса
][f к базису ][e :
fe
EF =
−1
. (3.7-9)
Рассмотрим другой случай, когда переход от базиса
][e к базису
][f задан парой матриц
{}{}
ffee
C,A,C,A
некоторой наблюдаемой системы. Запишем матрицу наблюдаемости
(3.3-7) и с учётом (3.6-8) проведём аналогичные предыдущим преобра-
зования:
ee
e
n
ee
eee
ee
n
ff
ff
f
f
N
AC
AC
C
AC
AC
C
N F
F
F
F
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅⋅
=
−
−
1
1
. (3.7-10)
Так как система наблюдаема, то
150
nNrankNrank
fe
=
= )()(
и матрица наблюдаемости имеет
n линейно независимых столбцов
[
]
n
zzzN
r
rr
⋅
⋅
⋅=
21
,
а квадратная матрица
[]
n
T
n
T
T
T
zzz
z
z
z
NN
rrr
r
r
r
⋅⋅⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅⋅
=
21
2
1
не вырождена. Умножим обе части равенства (3.7-10) слева на
T
e
N :
ee
T
ef
T
e
NNNN F= , (3.7-11)
откуда получим
f
T
ee
T
ee
NNNN
1
)(
−
=
F . (3.7-12)
Если система имеет скалярный выход, то
fee
NN
1−
=F . (3.7-13)
3.8. Канонические представления систем
3.8.1. Управляемое каноническое представление системы со ска-
лярным входом
Пусть в некотором исходном базисе
][h пространства состояний
X
записаны уравнения движения объекта со скалярным управлением:
)()()( tubtxAtx
hhhh
r
r
&
r
+=
; (3.8-1)
)(
)(
thh
xCty
rr
= . (3.8-2)
Более общая запись связывает не координатные столбцы, а сами
векторы в
X
x
∈
r
с помощью соответствующего оператора A :
)()()( tubtxtx ⋅+⋅=
r
r
&
r
A . (3.8-3)
Если система
{
}
b
r
,A управляема, то n векторов
bbb
n
rrr
1
,,
−
AA ,... образуют базис в пространстве X в силу того, что
nUrank = . Следовательно, в пространстве X в качестве базиса может
быть выбрана следующая система векторов:
