Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления

161

()

n

nn

n

i

A

C

γλγλλλλϕ

+++=−=

−

=

∏

...

1

3

, (3.9-15)

поэтому она имеет стандартный вид

⎥

⎦

⎤

⎢

⎣

⎡

−⋅⋅⋅−−−

⋅⋅⋅

⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅

⋅⋅⋅

⋅

=

−− 121

1000

0100

0010

γγγγ

nnn

C

U

A . (3.9-16)

С другой стороны, очевидно, что

UUU

C

U

LbAA

r

+= . (3.9-17)

Отсюда сразу же следует связь между коэффициентами характеристи-

ческого полинома (3.9-2) объекта и коэффициентами характеристическо-

го полинома (3.9-14) желаемой системы:

.,,2,1,

1

nil

inUii

K

=

+

−=−

+−

α

γ

(3.9-18)

Далее обусловлены следующие действия.

1. Задание желаемых собственных чисел замкнутой системы

33

2

3

1

,...,,

n

λ

.

2. Вычисление коэффициентов характеристического полинома замкну-

той системы

n

γ

,...,,

21

в соответствии с выражением (3.9-14).

3. Вычисление согласно (3.9-17) коэффициентов матрицы обратной

связи в базисе УКП:

nil

iiinU

,...,2,1 ,

1,

=

−

=

+−

γ

α

. (3.9-19)

4. Вычисление в соответствии с (3.9-12) и (3.8-17) матрицы обратной

связи в исходном базисе:

1−

=

HUUH

UULL . (3.9-20)

5. Определение величины коэффициента

v

k в соответствии с требова-

ниями по статике.

Так например, если требуется обеспечить единичную статику по

командному сигналу

v

, то это значит, что установившееся значение пе-

реходной функции

)(th замкнутой системы должно быть равно единице.

Одним из свойств передаточной функции устойчивой системы является

равенство:

)(lim)(lim

0

pWth

vy

pt

→∞→

= . (3.9-21)

162

Согласно структурной схеме, приведённой на рис. 3.9, передаточная

функция между командным

v

и выходным

y

сигналами имеет вид:

)()( pWkpW

v

vy

⋅= , (3.9-22)

где передаточная функция )(

p

W , может быть определена аналогично

выражению (3.8-22). Таким образом, получаем:

()

1

==∞

n

U

v

c

kh

γ

, (3.9-23)

откуда окончательно,

1U

n

v

c

k

γ

=

. (3.9-24)

163

3.10. Синтез управления в многомерной системе. Задача

разделения каналов

В предыдущих разделах, посвящённых синтезу, рассматривались

объекты со скалярным управлением (входом) и скалярным выходом. На

практике встречаются и более сложные объекты. Один из них был упо-

мянут в разделе 2.2. Это смесительный бак, у него две входные величи-

ны – два входных потока с различными концентрациями растворённого

вещества, и две выходных – концентрация

и расход выходного потока. В

качестве другого примера может быть взят объект, связанный с пере-

моткой некоторой полосы с одного рулона на другой. Для этого объекта

выходные переменные – это натяжение и линейная скорость перемотки;

входные – напряжения или токи приводных двигателей моталки и раз-

матывателя. Наконец, самолёт. В качестве выходных переменных могут

выступать углы тангажа, курса и крена; в качестве входных, управляю-

щих, - угловые положения руля высоты, руля направления и элеронов.

Как правило, в таких объектах каждая выходная величина зависит

от всех входных. В то же время, при синтезе управления такими объек-

тами часто требуется обеспечить не только заданные динамические и

статические

свойства системы, но и независимое управление по каждой

из выходных переменных.

Пусть уравнения объекта имеют вид

)()()( tuBtxAtx

r

&

r

+= ; (3.10-1)

)()( txCty

rr

= , (3.10-2)

где размерность вектора состояния

]1[

×

n , вектор управления и вектор

выхода имеют одинаковую размерность

]1[

×

p

. Такую же размерность

имеет вектор командного сигнала

v

r

, поступающий на вход системы.

Требуется синтезировать управление

u

r

такое, чтобы:

1) i –я составляющая вектора выхода

i

y зависела только от i –й

составляющей командного сигнала

i

v ;

2) по каждому из каналов была обеспечена заданная динамика,

иными словами, передаточная функция

)(

,

pV

pY

pW

i

yv

ii

=

, имеющая за-

данные полюсы;

3) для каждого из каналов был обеспечен заданный статический

коэффициент передачи.

3.10.1. Разделение исходного объекта на подсистемы интеграторов

Представим (3.10-2) в виде

164

x

C

xCy

p

r

M

rr

⎥

⎦

⎤

⎢

⎣

⎡

==

2

1

,

где

i

C - строки матрицы C . Тогда i -я координата вектора выхода

xCy

ii

r

= .

Рассмотрим процедуру многократного дифференцирования коор-

динат вектора выхода:

)1()1(21)(

)2()1(23)3(

2

...

;

−−−

++++=

+++=

′

++=

′′

+==

′

m

i

m

i

m

i

m

i

m

i

iiiii

iiii

uBCuBACuBACxACy

uBCuABCuBACxACy

uBCuABCxACy

uBCxACxCy

rrrr

LLLLLLLLLLLLLLLLLLLL

rrrr

rrr

r

&

r

(3.10-3)

Сократим запись:

∑

−

=

−−−

++=

1

)(11)(

m

i

m

i

m

i

m

i

uBACuBACxACy

ν

νν

r

(3.10-4)

Для каждой координаты найдем максимальное число дифферен-

цирований, при котором еще не появляется производная вектора

u

r

, то

есть, найдем такие числа

i

m

, что

0

1

≠

−

BAC

i

m

i

и 0

2

=

−

BAC

i

m

i

.

Таким образом, получим систему уравнений:

.

;

1)(

1

22

)(

2

1

11

)(

1

222

111

uBACxACy

ppp

m

p

m

p

m

p

mmm

rr

LLLLLLLLLLL

rr

r

−

+=

(3.10-5)

Запишем эту систему равенств в векторно-матричном виде:

uBxFuB

AC

x

AC

y

ppp

m

rrr

M

r

MM

**

1

2

1

2

1

)(

1

)(

2

)(

1

2

1

2

1

2

1

+−=

⎥

⎦

⎤

⎢

⎣

⎡

+

⎥

⎦

⎤

⎢

⎣

⎡

=

⎥

⎦

⎤

⎢

⎣

⎡

−

. (3.10-6)

165

Обозначим

⎥

⎦

⎤

⎢

⎣

⎡

=

)(

1

)(

2

)(

1

2

1

p

m

y

q

M

r

(3.10-7)

и

⎥

⎦

⎤

⎢

⎣

⎡

−=

p

m

AC

F

1

2

1

*

2

1

M

;

⎥

⎦

⎤

⎢

⎣

⎡

=

−

1

2

1

*

2

1

p

m

AC

B

M

. (3.10-8)

Тогда (3.10-6) можно переписать в виде

uBxFq

r

**

+−= . (3.10-9)

Если задача разделения каналов имеет решение, то матрица

*

B

не

вырождена и:

xFBqBu

r

*

1

*

1

*

−−

+=

. (3.10-10)

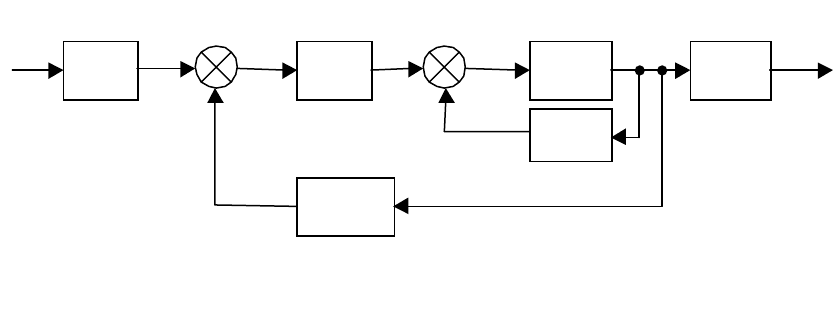
На рис. 3.10 представлена промежуточная структурная схема, со-

ответствующая уравнениям (3.10-1), (3.10-2) и (3.10-8).

Рис. 3.10. Промежуточная структурная схема

В

*

-1

В

∫

A

C

B

*

-

1

F

*

→

q

→

u

→

x

→

y

Для этой схемы справедливы уравнения

.

;)(

1

**

1

*

xCy

qBBxFBBAx

rr

r

&

r

=

++=

−−

(3.10-11)

Обозначим

.

;

1

*

1

*

−

∨

−

∨

=

+=

BBB

FBBAA

(3.10-12)

166

Теперь (3.10-11) превратится в

⎪

⎩

⎪

⎨

⎧

=

+=

,

;

VV

xCy

qBxAx

rr

r

&

r

(3.10-13)

а структурная схема промежуточной системы с входным вектором

q

r

примет вид, представленный на рис. 3.11.

Рис. 3.11. Структурная схема системы

относительно входного вектора

q

r

B

V

A

V

→

q

→

x

→

y

∫

C

С другой стороны, вектор выхода

y

r

связан с вектором q

r

равенством

(3.10-7) и поэтому схеме, представленной на рис. 3.11 полностью экви-

валентна схема, составленная из

p

подсистем последовательно вклю-

чённых интеграторов. Эта схема представлена на рис. 3.12.

q

1

q

i

q

p

∫

m

1

интеграторов

∫

m

i

интеграторов

∫

m

p

интеграторов

y

1

y

i

y

p

∫

Рис. 3.12. Структурная схема объекта, представленного в

виде изолированных подсистем интеграторов

Общее количество интеграторов не может быть больше n , то есть:

167

∑

=

≤

p

i

nm

1

.

Таким образом, система

} , {

VV

BA (3.10-13), у которой в качестве входного

вектора выбран вектор

q

r

,

а) развязана по каналам, то есть

i

y зависит только от

i

q для всех

значений

i ;

б) имеет

∑

=

p

i

m

1

собственных значений, равных нулю.

Теперь систему

} , {

VV

BA нужно попытаться привести к удобному ба-

зису, в котором синтезировать обратную связь, реализующую желаемые

собственные числа по каждому каналу.

Прежде всего, установим некоторые свойства матриц

V

A и

V

B . Ана-

логично (3.10-4) запишем:

∑

−

=

−−−

++=

1

)(

V

1

VV

1

VV

)(

m

i

m

i

m

i

m

i

qBACqBACxACy

iii

i

ν

r

.

С другой стороны,

i

m

i

qy

i

=

)(

. Отсюда следует:

1)

0

V

=

i

m

i

AC для всех i = 1,2,…,p ; (3.10-14)

2)

[]

i

ny

p

m

i

m

i

q

bbbACqBAC

ii

=

⎥

⎦

⎤

⎢

⎣

⎡

⋅=

−−

M

rrr

r

2

1

V

2

V

1

VV

1

V

...

, (3.10-15)

откуда:

1

V

1

V

=

−

i

m

i

bAC

i

r

; (3.10-16)

0

V

1

V

=

−

j

m

i

bAC

i

r

, при i

j

≠

; (3.10-17)

3)

0

V

=

−

j

m

i

bAC

i

r

ν

для 1>

ν

и для всех

j

, i . (3.10-18)

3.10.2. Преобразование базиса в пространстве

n

R

Перейдём от исходного базиса ][e к новому базису ][f с помощью

некоторой матрицы преобразования

е

F . При выборе базиса ][f учтем,

следующие обстоятельства:

• Объект управляем, поэтому ранг матрицы управляемости

168

[]

V

1

V

1

V

1

V

2

V

1

... ... ... ...

p

nn

pp

bAbAbAbAbbbU

r

MM

r

M

r

−−

=

(3.10-19)

равен порядку системы;

• так как каждый канал этой системы с размерностью

i

m управ-

ляем, то столбцы

V

1

V

1

V

1

V

1

,...,, ,... ,,...,,

1

p

m

pp

m

bAbAbbAbAb

p

r

−−

линейно независимы.

Теперь выберем базис

][f , соответствующий следующим коорди-

натным столбцам:

;;...;;

11

2

21

1

11

∨∨

−

∨

−

∨

=== bfbAfbAf

me

m

e

m

e

r

;;...;;

22

2

22

1

21

2

1

2

1

∨

+

∨

−

∨

+

∨

−

∨

+

=== bfbAfbAf

mme

m

me

m

me

r

(3.10-20)

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

;;;

...

2

...

1

1...

12111

∨

++

∨

−

∨

++

∨

−

∨

+++

===

−−

pmmep

m

mmeep

m

mme

bfbAfbAf

p

r

Если

∑

=

<

p

i

nm

1

, то оставшуюся часть векторов базиса

[

]

ост

f можно выби-

рать, перебирая оставшиеся столбцы матрицы

U :

V

1

V

1

V

1

V

111

,..., bAbAbA

mm

r

−+

ν

до тех пор, пока следующий вектор

V

1

V

bA

r

ν

не будет выражаться в виде

линейной комбинации всех предыдущих векторов базиса. Далее доба-

вим

V

2

1

V

2

V

22

, bAbA

mm

r

+

и так далее, пока число векторов базиса не достиг-

нет числа n . Тогда матрица преобразования базиса ][e в базис ][f бу-

дет иметь вид

[]

][

V

2

V

2

1

V

1

V

1

2

V

1

V

211

остp

mmm

e

fbbbAbbAbA

∨

−−

∨

−

=

r

L

r

L

r

L

r

L

r

L

r

F .

Рассмотрим вид матрицы

V

B в базисе ][f . Первый столбец этой

матрицы, то есть вектор

1

b

r

совпадает с

1

m -м столбцом базиса ][f ; вто-

рой столбец матрицы

B , то есть вектор

2

b

r

совпадает с )(

21

mm + -м

столбцом базиса

][f и так далее. Следовательно,

169

⎥

⎦

⎤

⎢

⎣

⎡

=

000

00

2

1

L

r

L

LLLL

L

r

L

r

p

f

B

β

, (3.10-21)

где

строк.

1

0

ii

m

⎪

⎭

⎪

⎬

⎫

⎥

⎦

⎤

⎢

⎣

⎡

=

L

r

β

(3.10-22)

Теперь обратим внимание на матрицу

С . В соответствии с (3.6-8)

CС

f

=

е

F

[]

⎥

⎦

⎤

⎢

⎣

⎡

=⋅

⎥

⎦

⎤

⎢

⎣

⎡

=

n

epep

ee

eee

p

fCfC

fff

C

r

L

r

LLL

r

L

r

L

r

L

rr

M

1

21

22

11

2

1

. (3.10-23)

Из этого равенства с учётом (3.10-14), (3.10-16), (3.10-17) получим:

⎥

⎦

⎤

⎢

⎣

⎡

=

000

2

1

p

f

s

C

L

MMMMM

L

, (3.10-24)

где

[]

4434421

L

i

m

i

s 001

=

. (3.10-25)

Наконец, займемся матрицей

V

f

A . Прежде всего, рассмотрим важ-

ную интерпретацию элементов матрицы

f

A . В соответствии с (3.6-8)

=

f

А

1−

е

F

е

А

е

F ,

поэтому

е

F =

f

А

е

А

е

F . (3.10-26)

170

Левую часть этого равенства можно расписать следующим образом:

е

F =

f

А

[]

=

⎥

⎦

⎤

⎢

⎣

⎡

⋅

f

nn

f

n

f

n

f

n

ff

eee

aaa

fff

n

L

MMMM

L

rrr

21

11211

...

21

[]

nnn

e

f

nne

f

ne

f

ne

f

e

f

ne

f

fafafafafafa

r

L

r

rrr

++++++= .........

111

1212111

.

С другой стороны:

е

А

е

F

[]

n

eеeе

fАfА

r

L

r

1

= .

Таким образом, получаем:

en

f

nie

f

ie

f

ieie

fafafafA

r

rrr

+++= ...

2211

. (3.10-27)

Это означает, что элементы

i -го столбца матрицы

V

f

A

⎥

⎦

⎤

⎢

⎣

⎡

=

f

ni

f

i

f

i

f

i

a

L

r

2

1

являются коэффициентами разложения произведения

eieei

fAfA

r

∨

≡ по

координатным векторам

enee

fff

r

rr

,...,,

21

.

Используя , (3.10-20), сопоставим произведения

ei

fA

r

∨

с координат-

ными столбцами векторов базиса

][f :

.

;

21

2

3

11

1

2

11

1

LLLLLLLL

r

e

m

e

m

e

m

e

fbAfA

bAfA

==

=

∨

−

∨∨

∨

−

∨∨

∨

∨∨

(3.10-28)

Так как

1

V

e

fA ,

1

V

1

+me

fA т. д. не совпадают ни с одним из собственных

векторов с номерами от 1 до

1

−−

∑

=

p

i

mn , то в соответствующих столб-

цах матрицы

V

f

A на позициях строк с номерами, большими

p

, могут на-

ходиться ненулевые элементы. Такие ячейки матрицы помечены симво-

Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления

Подождите немного. Документ загружается.