Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

191
0
=
−
−
q
qy
q
CCGAC L . (3.11-45)
Тогда получим уравнение для ошибки наблюдателя
)()( tt
q
q
q
Δ=Δ
r
&
r
L . (3.11-46)
Если назначить матрицу
q
L так, чтобы её собственные числа лежали в
левой полуплоскости достаточно далеко от мнимой оси, то ошибка на-
блюдателя, имеющая изначально место при ненулевых начальных ус-
ловиях, будет с соответствующей скоростью стремиться к нулю. Так же
быстро вектор
⎥
⎦
⎤
⎢
⎣
⎡
=
−
q
y
Ctx
p
r
r
)
r
1
)( (3.11-47)
будет стремиться к вектору
)(tx
r
. Вытекающее из (3.11-45) уравнение
CGCAC
y
q
q
q
=
−L (3.11-48)
называется матричным уравнением Люенбергера.
Теперь учтём, что задача построения наблюдателя, то есть нахож-
дения оценки
x
)
r
вектора состояния
x
r
возникла из-за необходимости
реализовать управление
)()()( tvktxLtu
v
r
rr
+= . (3.11-49)
Сама по себе оценка вектора состояния часто не нужна. Поэтому попы-
таемся найти оценку
∧
x
L
r
линейной комбинации координат вектора со-
стояния
x
L
r
. Будем искать эту оценку в виде
)()()( tytqtxL
r
)
r
r
ηχ
+=
∧
. (3.11-50)
Так как с течением времени
q
)
r
стремится к q
r
, то с учётом (3.11-38) и
уравнения выхода объекта получим
)()()( txCtxCtxL
q
r
rr
ηχ
+=
∧
, (3.11-51)
откуда следует
CCL
q
η
χ
+= . (3.11-52)
Таким образом, необходимо решить следующую систему матричных
уравнений:
.
;
LCC
CGCAC
q
y
q
q
q
=+
=−
ηχ
L
(3.11-53)
192
Эта система всегда имеет решение, если, во-первых, собственные чис-
ла матриц
q
L и
A
не совпадают друг с другом и, во-вторых, размер-
ность вектора
q
r
(размерность матрицы наблюдателя
q
L )
)1( −≥
ν
u
ns , (3.11-54)
где
u
n - размер вектора управления;
ν
- индекс наблюдаемости. Это та-
кое число, для которого матрица
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−1
~
ν
CA
CA
C
N
L
(3.11-55)
имеет ранг, равный
n .
Таким образом, может быть сформулирован следующий итоговый
алгоритм.
1. Найти индекс наблюдаемости
ν
и размерность наблюдателя s .
2. Задать желаемую динамику наблюдателя и записать матрицу его
динамики
q
L в виде матрицы, сопровождающей свой характери-
стический полином.
3. Вычислить матрицы
η
χ
,,,
y
q
GC согласно (3.11-53), а также мат-
рицу
u
G согласно (3.11-44).
4. Реализовать алгоритмы регулятора, включая наблюдатель Люен-
бергера минимального порядка:
).()()()(
;)()()()(
tvktytqtu
tuGtyGtqtq
v
uyq
rr
)
r
r
r
r
)
r
&
)
r
++=
++=
ηχ
L
(3.11-56)
193
3.12. Синтез реализуемого управления, обеспечивающий
заданные динамические и статические свойства систе-
мы управления
3.12.1. Динамические свойства системы с обратной связью и на-
блюдателем полного порядка
Предполагается, что известны уравнения управляемого и наблю-
даемого объекта:
⎪
⎩
⎪
⎨
⎧
=
+=
).()(
);()()(
txCty
tubtxAtx
rr
r
r
r
&
r
(3.12-1)
Кроме того, проведён синтез управления и получены матрица
L и ко-
эффициент
v
k для равенства
)()()( tvktxLtu
v
r
rr
+= , (3.12-2)
обеспечивающего желаемые собственные числа замкнутой системы
з
з
2
з
1
... , ,
n
λ
λ
λ
, или нули характеристического полинома замкнутой систе-
мы
nn
nn
A
C
γ
λ
γ
λ
γ
λ
λ
ϕ
+
+
++=
−
−
1
1
1
...)( . (3.12-3)
Предполагается также, что имеется наблюдатель
)()()()()( tyKtuBtxKCAtx
r
r
)
r
&
)
r
++−= , (3.12-4)
спроектированный таким образом, что его характеристический полином
)(
λ
ϕ
L
имеет коэффициенты
n
β
β
β
... , ,
21
, соответствующие некоторой
выбранной совокупности собственных чисел
N
n
NN
λ
λ
λ
,...,,
21
.
Учтём, что при формировании управления фактически можно восполь-
зоваться не самим вектором состояния
x
r
, а лишь его оценкой
x
)
r
, то есть
)()()( tvktxLtu
v
r
)
rr
+= . (3.12-5)
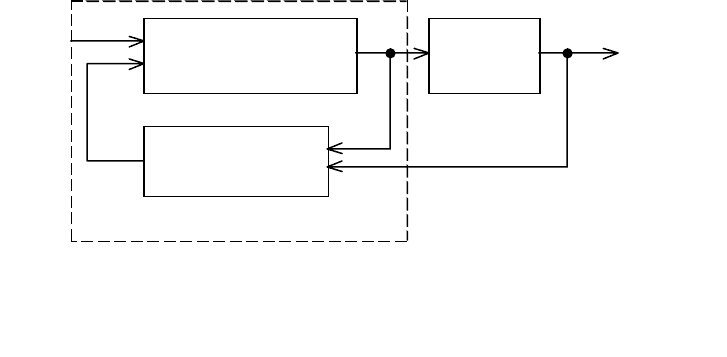
Таким образом, рассматривается функциональная схема полной
системы (объект, формирователь управления и наблюдатель), пред-
ставленная на рис. 3.18
194
наблюдате ль
)( tv
r
)(tu
r
формирователь
управления
)(ty
r
регулятор
объект
x
)
r
Рис. 3.18. Функциональная схема полной
системы
Запишем уравнения этой системы, то есть, совместно уравнения
объекта с управлением и наблюдателя
⎪
⎩
⎪
⎨
⎧
+++−=
++=
).()()()()()(
);()()()(
txKCtvBktxBLtxKCAtx
tvBktxLbtxAtx
v
v
rr
)
r
)
r
&
)
r
r
)
r
r
r
&
r
(3.12-6)
С использованием блочных матриц получим
)(
)(
)(
)(
)(
tv
Bk
Bk
tx
tx
BLKCAKC
BLA
tx
tx
v
v
r
)
r
r
&
)
r
&
r
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
+−
=
⎥
⎦
⎤
⎢
⎣
⎡
. (3.12-7)
Поведение этой системы зависит от собственных чисел матрицы дина-
мики полной системы
⎥
⎦
⎤
⎢
⎣
⎡
+−
=
BLKCAKC
BLA
X
. (3.12-8)
Надо попытаться для
X
найти некоторую подобную матрицу, такую,
чтобы можно было легко определить её собственные числа. Перейдём к
подобной матрице с помощью преобразования
hhhf
F
X
F
X
1−
= . (3.12-9)
Матрицу
h
F выберем следующей:
⎥
⎦
⎤
⎢
⎣
⎡
−
=
nn
nn
e
EE
E 0
F
, (3.12-10)
где индекс
n указывает на размеры соответствующих нулевой и еди-
ничных матриц. Легко убедиться, что
hh
FF =
−1
. В результате получим:
⎥
⎦
⎤
⎢
⎣
⎡
−
−+
=
⎥
⎦
⎤
⎢
⎣
⎡
−
⎥
⎦
⎤
⎢
⎣
⎡
+−
⎥
⎦
⎤
⎢
⎣
⎡
−
=
KCA
BLBLA
EE
E
BLKCAKC
BLA
EE
E
nn
n
nn
n
f
0
00
X .
195
Характеристический полином матрицы
X
не зависит от базиса и опре-
деляется следующим образом:
[]
)()(det)(
2
KCAEBLAEE
nnn
−
−
⋅
+
−
=
−
=
λ
λ
λ
λ
ϕ
X
X
.
Отсюда следует
)()()(
λ
ϕ
λ
ϕ
λ
ϕ
LX
C
A
= . (3.12-11)
Таким образом, полная система, в которой управление вычисляется в
функции оценки вектора состояния, имеет
n2 собственных чисел:
з
з
2
з
1
... , ,
n
λ
λ
λ
,
N
n
λ
λ
λ
... , ,
N
2
N
1
. Собственные числа замкнутой системы со-
хранили те собственные числа, были заданы при синтезе управления.
Отметим, что в полной системе передаточная функция от ко-
мандного сигнала
v
r
до выходного сигнала y
r
тождественно равна пере-
даточной функции в идеализированной системе без наблюдателя. Это
действительно так, потому что по определению передаточная функция
связывает изображения соответствующих переменных при нулевых на-
чальных условиях. При нулевых начальных условиях выход объекта
y
r
и
выход
наблюдателя y
)
r
тождественно равны.
3.12.2. Динамические свойства системы с обратной связью управ-
лением и наблюдателем минимального порядка
В случае использования наблюдателя минимального порядка в
соответствии с (3.11-56) и (3.11-44) уравнения регулятора имеют вид
.)()()()(
;)()()()(
tvktytqtu
tuBCtyGtqtq
v
q
yq
rr
)
r
r
r
r
)
r
&
)
r
++=
++=
ηχ
L
С учётом управления запишем совместно уравнения объекта и наблю-
дателя:
.)()()()()()(
;)()()()()(
tvBkCtqBCtqtxCBCtxCGtq
tvBktqBtxCBtxAtx
v
qq
q
q
y
v
r
)
r
)
r
rr
&
)
r
r
)
r
r
r
&
r
++++=
+++=
χη
χη
L
(3.12-12)
Отсюда матрица динамики полной системы имеет вид:
⎥
⎦
⎤
⎢
⎣
⎡
++
+
=
χη
χ
η
BCCBCCG
BCBA
q
q
q
y
L
X
. (3.12-13)
Перейдём к подобной матрице с помощью преобразования (3.12-9), где
196
⎥
⎦
⎤
⎢
⎣
⎡
−
==
−
sq
n
ee
EC
E 0
1
FF . (3.12-14)
В результате, учитывая (3.11-52) и (3.11-48), получим:
⎥
⎦
⎤
⎢
⎣
⎡
−
+
=
q
f
BBLA
L
X
0
χ
. (3.12-14)
Отсюда следуют те же выводы, что и полученные выше для системы с
наблюдателем полного порядка.
3.12.3. Результирующий алгоритм синтеза для системы с одним
входом и одним выходом
1. Для матрицы объекта A вычислить характеристический полином
)(
λ
ϕ
A
и зафиксировать его коэффициенты
n
α
α
α
..., , ,
21
.
2. В соответствии с требованиями к динамике замкнутой системы задать
желаемые значения собственных чисел
з
з
2
з
1
... , ,
n
λ
λ
λ
, вычислить
∏
=
+=
n
i
A
C
1
3
)()(
λλλϕ
,
то есть найти коэффициенты желаемого характеристического поли-
нома
n
γ
γ
γ
..., , ,
21
.
3. Рассчитать матрицу обратной связи в базисе УКП:
[
]
nuuuU
lllL
⋅
⋅⋅=
21
, где
jnjnju
l
−+−+
−
=
11
γ
α
.
4. Задать желаемые собственные числа наблюдателя
N
n
NN
λ
λ
λ
,...,,
21
и
вычислить коэффициенты характеристического полинома наблюда-
теля:
n
β
β
β
... , ,
21
.
5. Рассчитать матрицу обратной связи наблюдателя в базисе ИКП:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
In
I
I
I
I
k
k
k
k
K
M
3
2
1
, где
jnjnjI
k
−+−+
−
=
11
α
β
.
6. Рассчитать матрицу перехода от исходного базиса к базису УКП
1−
=
Uh
UUU , матрицу выхода в этом базисе
hU
CC U
=
и, при наличии

197
требования обеспечить единичную статику, вычислить коэффициент
по командному сигналу
1U
n
v
C
k
γ
= .
7. Рассчитать матрицу перехода от базиса
][u (УКП) к базису ][i (ИКП)
UIU
NN ⋅=
−1
I и обратную ей матрицу.
8. Рассчитать вектор
b
r
в базисе ИКП, используя переход от базиса УКП
UUI
bb
rr
1−
= I .
9. Рассчитать матрицу обратной связи
L в базисе ИКП, используя пере-
ход от базиса
][u к базису ][i :
UUI
ILL
=
.
10. Записать уравнение наблюдателя в базисе ИКП:
()
)()()()( tvkbtyKtxLbCKAtx
v
IIIIIIIII
r
r
)
r
r
&
)
r
+++−= .
11. Записать уравнение для формирования управления:
)()()( tvktxLtu
v
II
+=
)
r
.
Уравнения, полученные в пунктах 10 и 11 – это уравнения регуля-
тора. Следует подчеркнуть, что в них используется вектор оценки со-
стояния объекта, записанный не в исходном базисе, а в базисе иденти-
фикационного канонического представления.
3.12.4. Итоговые примеры полного синтеза систем управления
3.12.4.1. Система со скалярными входом и выходом и наблюда-
телем полного порядка
Задан объект, представленный структурной схемой на рис. 3.19.
Рис. 3.19. Структурная схема объекта
y
x
1
x
2
u
2
Требуется синтезировать реализуемое управление, обеспечивающее
единичную статику по командному сигналу, а также динамику основного
контура системы и наблюдателя в соответствии с желаемыми собствен-
ными числами
;55
2,1
j
з
±
−=
λ
.10
21
−
=
=
NN
λ
λ
Ниже приведены промежуточные результаты расчёта.
Матрица управляемости объекта и ей обратная в исходном базисе:
198
⎥
⎦
⎤
⎢
⎣
⎡
−
=
11
10
U
;
⎥
⎦
⎤
⎢
⎣
⎡
=
−
01
11
1
U .
Матрица управляемости объекта и ей обратная в базисе УКП:
;
31
10
⎥
⎦
⎤
⎢
⎣
⎡
−
=
U
U
01
13
1
⎥
⎦
⎤
⎢
⎣
⎡
=
−
U
U .
Коэффициенты характеристического полинома объекта, желаемой сис-
темы и наблюдателя:
⎥
⎦
⎤
⎢
⎣
⎡
=
2
3
α
r
; .
⎥
⎦
⎤
⎢
⎣
⎡
=
50
10
γ
r
;
⎥
⎦
⎤
⎢
⎣
⎡
=
100
20
β
r
.
Матрица обратной связи в базисе УКП:
[]
748
−
−=
U
L .
Матрица наблюдателя:
17
98
⎥
⎦
⎤
⎢
⎣
⎡
=
I
K .
Матрица перехода от исходного базиса к базису УКП:
⎥
⎦
⎤
⎢
⎣
⎡
=
12
01
H
U .
Матрица выхода в базисе УКП:
[]
01=
U
C .
Коэффициент по командному сигналу
50
=
v
k .
Матрица наблюдаемости базисе УКП, обратная ей и та же матрица в ба-
зисе ИКП:
⎥
⎦
⎤
⎢
⎣
⎡
==
−
10
01
1
UU
NN ,
⎥
⎦
⎤
⎢
⎣
⎡
−
=
31
10
I
N .
Матрица перехода от базиса ИКП к базису УКП:
31
10
⎥
⎦
⎤
⎢
⎣
⎡
−
=
I
U .
Вектор передачи управления в базисе ИКП:
⎥
⎦
⎤
⎢
⎣
⎡
−
=
3
1
I
b
r
.
199
Матрица обратной связи в базисе ИКП:
[]
277 −−=
I
L .
Матрица динамики наблюдателя в базисе ИКП:
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=−=
201
1000
IIII
CKAL .
Результирующие уравнения регулятора:
.50277
;17320
;98100
21
212
21
vxxu
yuxxx
yuxx
+−−=
+−−=
++−=
))
))
&
)
)
&
)
В этих уравнениях индекс
i при координатах вектора оценки состояния
опущен.
3.12.4.2. Система со скалярными входом и выходом и наблюда-
телем пониженного порядка
Для объекта, заданного на рис.3.19, построить наблюдатель пони-
женного порядка. Учесть, что управление объектом строится на основе
собственных чисел замкнутой системы
j
з
55
2,1
±
−
=
λ
.
Для этого объекта
[]
01 ;
1
0
;
10
12
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
= CBA ,
собственные числа объекта -
2,1
21
−
=
−
=
λ
λ
.
Порядок объекта
2=n , размерность выхода 1=
y
n , следователь-
но, размерность наблюдателя пониженного порядка
1=
q
n .
Зададимся собственным числом наблюдателя
10
1
−=
Н
λ
(оно
должно располагаться на комплексной плоскости левее собственных чи-
сел замкнутой системы).
Так как
1
xy = , то примем
2
xq
=
. Тогда
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
2
1
10
01
x
x
q
y
.
Таким образом, выбрана матрица
[]
10=
q
C .
200
Ей соответствует невырожденная квадратная матрица
⎥
⎦
⎤
⎢
⎣
⎡
==
−
10
01
1
pp
CC .
Соответственно получаем
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
1
0
;
0
1
qy
FF .
Теперь в соответствии с (3.11-33) определим
q
L :
[] []
KK
q
−−=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
−
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
⋅= 1
1
0
10
12
01
1
0
10
12
10
L .
Поскольку назначено
10−=
Н
λ
, то
101 −=−− К и 9
=
К .
Таким образом,
10−=
q
L , и первое уравнение наблюдателя принимает
вид:
uy +−−= 7210
ξξ
&
.
Запишем оценку для
x
r
:
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
−
=
2
1
ˆ
ˆ
1
0
)(
9
1
)(
ˆ
x
x
tytx
ξ
r
.
Отсюда
ξ
+= yx 9
ˆ
2
.
Замкнем систему (сформируем управление). В п.3.12.4.1 была рас-
считана матрица обратной связи
[]
748
−
−=
U
L .
Переведем её в исходный базис:
[
]
734
11
−
−
=
=
=
−−
eUUeU
UULLL U .
Таким образом, управление принимает вид
vxyu 50734
2
+
−
−
=
.
Структурная схема полной схемы с регулятором и с наблюдателем по-
ниженного порядка представлена на рис. 3.20.
