Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

171
лом "
×". Кроме того, на данном этапе нет смысла рассматривать столб-
цы этой матрицы с номерами, большими
p
. В результате получаем вы-
ражение для матрицы
∨
A в базисе ][f :

172
0 1 0 … 0
0 0 1 … 0
………….
0 0 0 … 1
0 0 0 … 0
0 0 0 … 0
0 0 0 … 0
………….
0 0 0 … 0
0 0 0 … 0
:
:
:
:
:
0 0 0 … 0
0 0 0 … 0
………….
0 0 0 … 0
0 0 0 … 0
1
m
0 0 0 … 0
0 0 0… 0
…………
0 0 0 … 0
0 0 0 … 0
0 1 0 … 0
0 0 1 … 0
………….
0 0 0 … 1
0 0 0 … 0
:
:
:
:
:
0 0 0 … 0
0 0 0 … 0
………….
0 0 0 … 0
0 0 0 … 0
2
m
…………. …………. ………….
0 0 0 … 0
0 0 0 … 0
………….
0 0 0 … 0
0 0 0 … 0
0 0 0 … 0
0 0 0 … 0
………….
0 0 0 … 0
0 0 0 … 0
:
:
:
:
:
0 1 0 … 0
0 0 1 … 0
………….
0 0 0 … 1
0 0 0 … 0
p
m
* 0 0 … 0
………….
* 0 0 … 0
* 0 0 … 0
………….
* 0 0 … 0
:
:
:
* 0 0 … 0
………….
* 0 0 … 0
∑
−
i
mn
V
f
A =
1
m
2
m
p
m
∑
−
i
mn
Эту же матрицу удобнее записать в блочном виде:
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
0000201
0p
2022
1011
V
00
00
00
AAAA
AA
AA
AA
A
p
pp
f
L
L
MMMMM
L
L
. (3.10-29)
Разобьём вектор состояния
x
r
на систему )1(
+
p
частных векторов
и обозначим
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
0
2
1
z
z
z
z
x
p
f
r
r
M
r
r
r
, (3.10-30)
173
где
i
z
r
имеет размерность
[]
1
×
i
m . Тогда уравнения (3.10-13) в базисе
][f примут вид:
=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
0
2
1
z
z
z
z
p
&
r
&
r
M
&
r
&
r
∗
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
0000201
0
2022
1011
00
00
00
AAAA
AA
AA
AA
p
ppp
L
L
MMMMM
L
L
+
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
0
2
1
z
z
z
z
p
r
r
M
r
r
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∗
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
p
p
q
q
q
M
M
L
r
L
MMMM
L
r
L
r
2
1
2
1
000
00
00
00
β
β
β
;
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
∗
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
0
2
1
2
1
2
1
000
000
000
z
z
z
z
s
s
s
y
y
y
p
pp
r
r
M
r
r
L
MMMMM
L
L
M
. (3.10-31)
Отсюда следуют уравнения для частных подсистем:
iiiiiii
qzAzAz
β
r
r
r
&
r
++=
00
(3.10-32)
iii
zsy
r
=
,
()
pi ,...,2,1=
∑
=
+=
p
zAzAz
1
00000
ν
νν
r
r
&
r
. (3.10-33)
Раскроем систему дифференциальных уравнений для
i -й подсистемы:
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
+=
+=
+=
+=+=
−−
imimi
mimimi
iii
ii
i
ii
qgz
gzz
gzz
gzzazz
ii
iii
,,
1,,1,
232
120
10
121
.................
&
&
&
r
&
, (3.10-34)
{
1ii
zy =
где
10
1
i
a - первая строка матрицы
0i
A . Такой подсистеме соответствует
структурная схема, представленная на рис. 3.13.
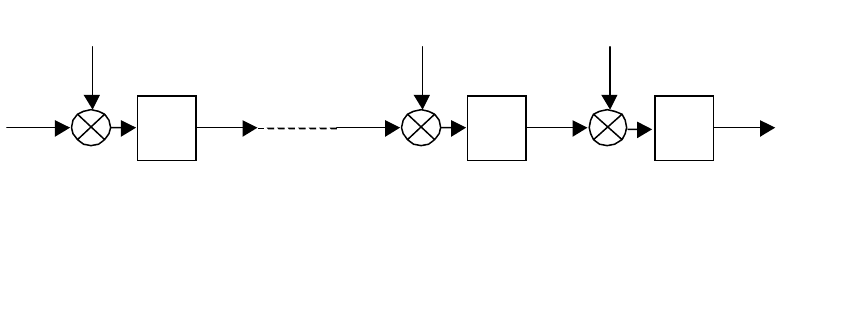
174
Рис. 3.13. Структурная схема частной подсистемы
1i
z
i
y
i
mi
z
i
mi
g
i
q
∫
2i
z
2i
g
3i
z
∫
1i
g
∫
Из сопоставления этой схемы со схемой, приведённой на рис. 3.12, сле-
дует:
а)
ii
yz =
1
;
)(
ν
ν
ii
yz = при 1>
ν
;
б)
0=
ν
i
q и 0
0
=
ν
A для
p
,...,2,1=
ν
.
Таким образом, выходы интеграторов частных подсистем, пока-
занных на рис. 3.12, совпали с координатами вектора
x
r
в базисе ][f .
Кроме того, все блочные матрицы
01000
,...,,
p
AAA в (3.10-29)- нулевые.
3.10.3. Формирование управления
Работая в базисе ][f , мы имеем
p
изолированных подсистем,
сумма выходов которых подаётся на вход общей подсистемы с матри-
цей динамики
00
A размерности
∑
=
−
p
i
i
mn
1
:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+=
=+=
=+=
∑
=
.
;;
...................
;;
1
00000
1
111111111
p
pppppppp
zAzAz
zyqzAz
zyqzAz
ν
νν
β
β
rr
&
r
r
r
&
r
r
r
&
r
(3.10-35)
Соответствующая структурная схем представлена на рис. 3.14.
Пары матриц
},{
iii
A
β
r
для
p
i ,...,2,1
=
имеют форму УКП, при-
чем, каждая из матриц
ii
A
имеет только нулевые собственные значения.
Это вполне согласуется с тем, что в п. 3.10.1 было произведено преоб-
разование объекта на подсистемы последовательно включённых инте-
граторов. Сформируем управление
i
q
для
p
i ,...,2,1
=
в следующем
виде:
)()( tzltvkq
ifiiii
r
+
=
, (3.10-36)
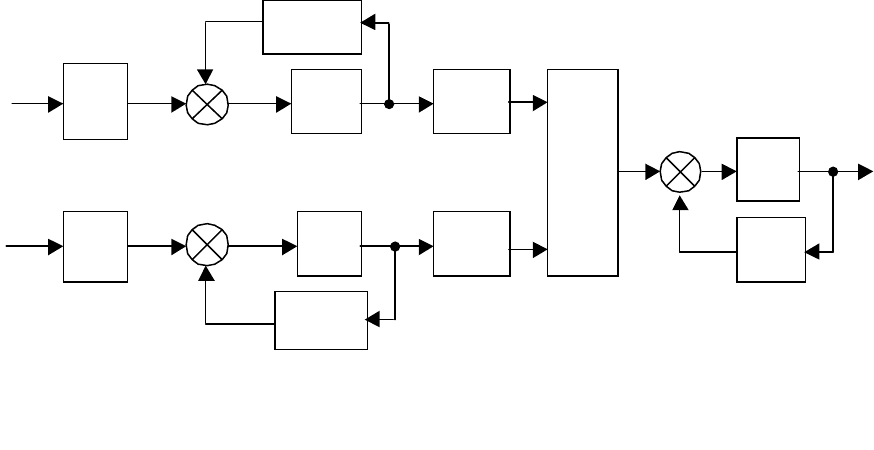
175
Рис. 3.14. Структурная схема объекта в базисе
][f
→
z
0
→
z
p
q
p
q
1
→
z
1
→
β
1
∫
А
11
А
01
→
β
p
A
p,p
∫
A
00
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
∫
A
0p
∑
где
[]
f
mi
f
i
f
ifi
i
llll
,21
K=
-
матрица обратной связи для
i -й подсистемы в базисе ][f .
Тогда получим следующее дифференциальное уравнение для
i -й под-
системы:
iiiifiiiiii
vkzlzAz
ββ
r
r
r
r
&
r
++=
,
или
iiiifii
vkzz
βχ
r
r
&
r
+= . (3.10-37)
Нетрудно убедиться, что матрица динамики
i -й подсистемы в базисе ][f
имеет вид
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
f
mi
f
i
f
i
f
i
fi
i
llll
,321
1000
0100
0010
L
L
MMMMM
L
L
χ
. (3.10-38)
Следовательно, определены характеристические полиномы подсистем:
f
i
m
f
mi
m
f
mi
m
i
lll
i
i
i
i
i
1
2
1,
1
,
...)( −−−−=
−
−
−
λλλλϕ
. (3.10-39)
Согласно (3.8-22) а также с учетом (3.10-13), (3.10-24) и (3.10-37) запи-
шем выражение для передаточной функции замкнутой
i -й подсистемы:

176
f
i
m
f
mi
m
i
yv
lplp
k
pW
i
i
i
ii
1
1
,
...
)(
−−−
=
−
. (3.10-40)
Очевидно:
f
i
i
yv
l
k
W
ii
1
)0(
−
=
. (3.10-41)
Задавая расположение полюсов и статику для каждой подсистемы,
в итоге получим матрицы:
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
∨
ppf
f
f
f
k
k
k
k
l
l
l
L
L
MMMM
L
L
L
MMMMM
L
L
00
00
00
;
000
000
000
2
1
,
2
1
. (3.10-42)
Возвращаясь в исходный базис для уравнений (3.10-13), получим:
f
LL =
V
1−
е
F . (3.10-43)
При этом вектор
q
r
формируется в соответствии с выражением
)()()(
V
tvktxLtq
r
r
r
∨
+= . (3.10-44)
Учитывая (3.10-10), окончательно получим:
VkxLtVkBxLBxFBu
r
r
rrr
+=++=
−−−
)(
V
1
*
V
1
**
1
*
, (3.10-45)
где
V
1
*
V
*
1
*
);( kBkLFBL
−−
=
+= . (3.10-46)
На этом можно закончить синтез, если часть системы, оказавшаяся вне
обратной связи, имеет допустимые динамические свойства. Если же нет,
например,
00
A - неустойчива, то приходится идти на то, чтобы ввести
обратную связь
0
L , по
0
z
r
, по крайней мере, через один из каналов )(
r
q ,
оставив полностью развязанными остальные
)1(
−
p
каналов. В этом
случае
0
V
,,
ffrr
llk нужно рассчитывать совместно. Связь
0
L должна обес-
печить «надзор» за бывшими ранее без контроля
∑
−
)(
i
mn полюсами
(собственными числами) системы. Эта часть расчета может быть произ-
ведена по обычной методике синтеза системы с одним входом. Резуль-
тирующая структура в базисе
][f приведена на рис. 3.15.
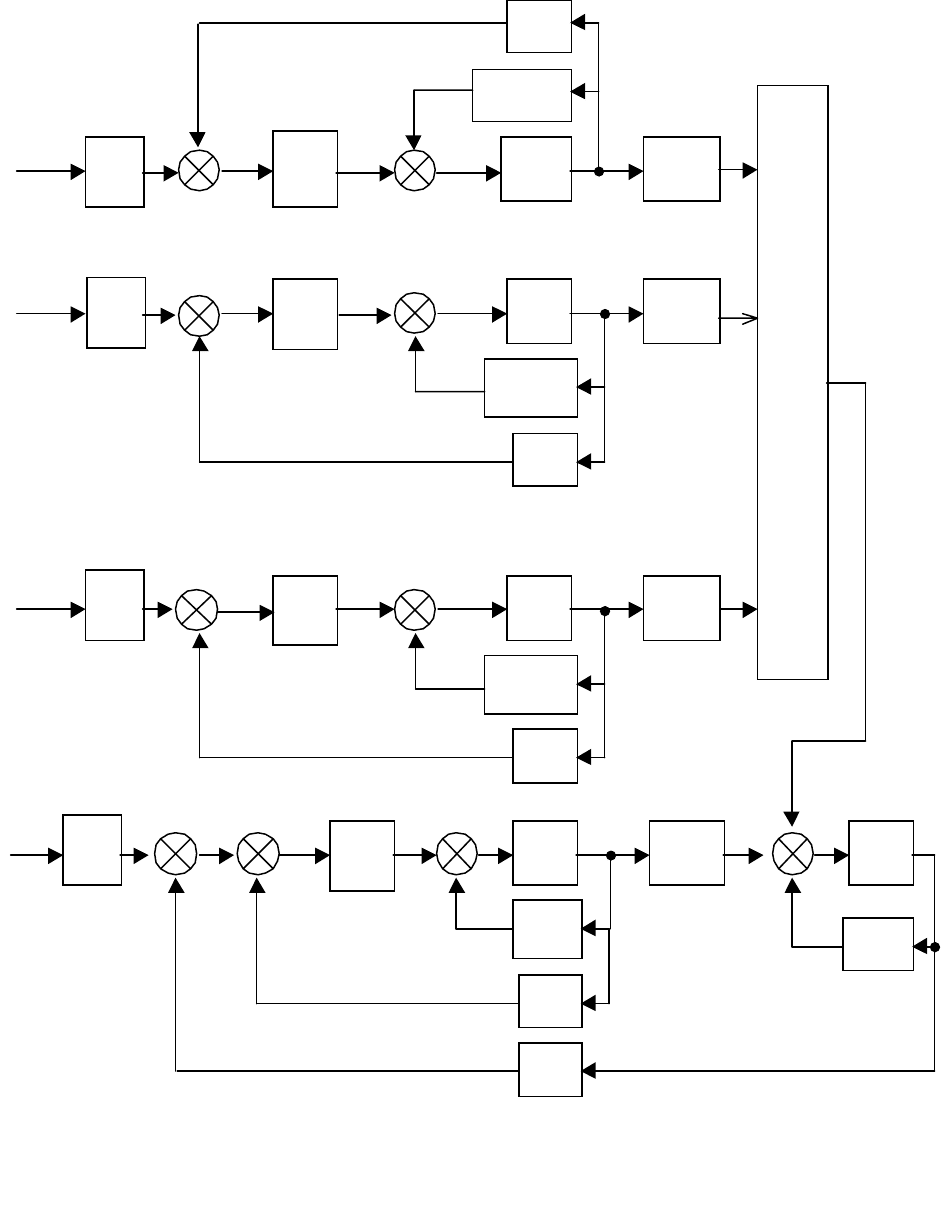
177
Рис. 3.15. Структурная схема системы в базисе
][
f
→
z
i
q
i
q
1
→
z
1
→
β
1
∫
А
11
А
01
→
β
i
A
i i
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
v
1
v
i
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
q
r
→
β
r
A
rr
v
r
→
z
j
∫
A
0i
∑
k
1
V
l
f1
k
i
V
l
fi
q
p
→
β
p
A
pp
v
p
→
z
p
∫
A
0p
k
p
V
l
fp
∫
A
0r
k
jr
V
l
fr
l
f0
∫
A
00
3.10.4. Итоговый алгоритм
1) Расчет чисел pim
i
,...,2,1, = :
⎩
⎨
⎧
=
≠
=
−
−
.0
;0
2
1
max
BAC
BAC
mm
m
i
m
i
i
(3.10-47)
178
Эти числа можно также находить непосредственно из схемы в перемен-
ных состояния.
2) Вычисление матриц
**
,BF :
. ;
1
1
1
*
1
*
11
B
AC
AC
B
AC
AC
F
pp
m
p
m
m
p
m
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
−
−
MM (3.10-48)
3) Вычисление
1
*
−
B . Если
*
B - вырождена, то задача разделения
каналов не имеет решения.
4) Вычисление матриц
VV
, BA :
{
1
*
V
*
1
*
V
;
v
−−
=
+
= BBBFBBAA
B
. (3.10-49)
5. Построение матрицы
e
F :
[]
⎥
⎦
⎤
⎢
⎣
⎡
=
−−
остp
mm
e
fbbbAbbA M
r
MM
r
MM
r
MM
r
MM
r
V
V
2
V
2
1
V
V
1
V
1
1
V
.........
21
F . (3.10-50)
6. Расчет коэффициентов характеристических уравнений каналов, то
есть строк
fi
l . Для этого предварительно должны быть заданы наборы
желаемых собственных чисел
),...,,(
21
i
miii
λ
λ
λ
по каждому из кана-
лов, после чего в соответствии с равенством
f
i
m
f
mi
m
f
mi
m
m
i
lll
i
i
i
i
i
i
1
2
1,
1
,
1
...)( −−−−=−
−
−
−
=
∏
λλλλλ
ν
ν
(3.10-51)
следует рассчитать
[]
f
mi
f
ifi
i
lll
,1
...= . (3.10-52)
и сформировать матрицу
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
fp
f
f
f
l
l
l
L
L
MMMM
L
L
00
00
00
2
1
..
7. Расчет (построение в соответствии с выбранным базисом) матрицы
00
A и вычисление ее собственных чисел.
8. Принятие решения о необходимости завязки каналов для коррекции
собственных чисел полинома
)(
0
λ
ϕ
. В случае необходимости - вы-
брать канал для коррекции и далее провести для него расчет по ме-
179
тодике синтеза системы с одним входом. В конечном итоге должна
быть получена
f
L - полная матрица обратной связи промежуточной
системы в базисе
][f .
9. Расчет матрицы
V
k по заданным коэффициентам :)0(
i
W
f
iii
lWk
1
V
)0(−= (3.10-53)
и
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
V
V
2
V
1
V
00
00
00
p
k
k
k
k
L
MMMM
L
L
. (3.10-54)
10. Расчет матрицы обратной связи промежуточной системы в исходном
базисе
.
1
V
−
=
ef
LL F (3.10-55)
11. Расчет результирующей матрицы обратной связи
)(
V
*
1
*
LFBL
+
=
−
. (3.10-56)
12. Расчет матрицы передаточных коэффициентов по вектору команд-
ных сигналов
V
1
*
kBk
−
= . (3.10-57)
Вектор управления формируется традиционным образом:
)()()( tvktxLtu
r
rr
+= . (3.10-58)
При необходимости может быть синтезирован идентификатор (наблю-
датель) неизмеряемых координат вектора состояния.
180
3.11. Основы построения идентификаторов состояния (на-
блюдателей)
3.11.1. Наблюдатель Люенбергера полного порядка
3.11.1.1. Синтез архитектуры наблюдателя
Рассмотрим линейную стационарную систему, которая описывает-
ся векторно-матричными дифференциальными уравнениями:
⎩
⎨
⎧
=
+=
).()(
);()()(
txCty
tuBtxAtx
rr
r
r
&
r
(3.11-1)
Для такой системы существуют алгоритмы модального синтеза, которые
позволяют найти управление:
)()()( tvktxLtu
r
rr
+= , (3.11-2)
обеспечивающее заданные динамику и статику системы. Проблема за-
ключается в необходимости использования вектора обратной связи для
формирования такого управления. Фактически в распоряжении разра-
ботчика системы управления лишь вектор выхода
)(ty
r
. Возникает во-
прос: как, наблюдая за вектором
)(ty
r
, восстановить вектор )(tx
r
, или
найти его оценку
)(tx
)
r
? При этом ошибка оценки вектора )(tx
r
)()()( txtxte
)
r
r
r
−= (3.11-3)
должна быть относительно малой, и тем более, с течением времени не
должна расти.
Будем полагать, что разработчику достаточно хорошо известны
параметры объекта, то есть оценки
CBA
)
)
)
, , , матриц CB
A
, , . Более
того, положим
CCBBAA ===
)
)
)
, , . (3.11-4)
В этом случае, если построить аналоговую или цифровую модель объ-
екта в соответствии с уравнениями
,)()(
);()(
txCty
tuBtxAx
)
r
)
r
r
)
r
&
)
r
=
+=
(3.11-5)
как показано на рис. 3.16, то можно было бы ожидать выполнения ра-
венств
x
x
r
)
r
= и yy
r
)
r
= . (3.11-6)
