Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

121
формах. Эту задачу в общем виде формализовать не удалось до сих
пор. В то же время, при проектировании систем выявилась важная зако-
номерность: эталонные процессы, к которым притягивается движение в
системе, должны соответствовать структуре управляемого объекта. Это
означает, что уравнения эталонной системы, отображённой на рис. 2.46,
должны иметь такой же вид,
как и уравнения объекта. Поэтому в качест-
ве эталонной системы можно выбрать систему того же порядка, что и
объект, но с собственными числами, а значит, и с характеристическим
полиномом, отвечающими требованиям, предъявляемым к замкнутой
системе.
Рассмотрим способ формирования ошибки
E
ε
, характеризующей
отклонение некоторой конкретной системы от эталонной. Пусть эталон-
ная система
n однородных дифференциальных уравнений первого по-
рядка приведена к одному дифференциальному уравнению
n -го поряд-
ка:
0...
)1(
1
)1(
1
)(
=
+
+++
−
−
ЭnЭn
n
Э
n
Э
xxxx
γ
γ
γ
. (2.11-5)
В левую часть равенства (2.11-5) вместо координаты
Э
x подставим
одну из координат вектора состояния объекта. Скорее всего, при этом
равенство нулю нарушится. Получаем уравнение невязки:
EОбnОбn
n
Об
n
Об
xxxx
ε
γ
γ
γ
=
+
+++
−
−
)1(
1
)1(
1
)(
... . (2.11-6)
Переменная
E
ε
характеризует отклонение процессов объекта от эта-
лонных. Она равна нулю на интервале времени
),0[ ∞
=
t только лишь в
том случае, когда процессы в объекте или в проектируемой системе
полностью тождественны процессам в эталонной системе.
Учтём уравнение объекта
)()()( tuBtxAtx
r
r
&
r
+= (2.11-7)
и приведём уравнение (2.11-6) к такому виду, чтобы в него входили
только координаты векторов состояния
x
r
и управления
u
r
:
).()(...)()(
)(...)()(
2211
2211
ttuqtuqtuq
txqtxqtxq
Enunuu
nxnxx
uu
ε
=+++
+
+++
(2.11-8)
Это уравнение, используя очевидные обозначения, можно записать ина-
че:
)()()( ttuqtxq
E
T
u
T
x
ε
=
+
r
r
r
r
. (2.11-9)
В соответствии с введённой текущей ошибкой
)(t
E
ε
может быть исполь-
зован интегральный критерий качества (функционал)
∫
∞
=
0
2
)( dttJ
E
ε
. (2.11-10)

122
Квадрат ошибки можно записать с помощью квадратичных форм:
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
=
)(
)(
)(
)(
)(
)(
)(
)(
2
tu
tx
qqqq
qqqq
tu
tx
tu
tx
q
q
q
q
tu
tx
T
uu
T
xu
T
ux
T
xx
T
T
u
x
u
x
T
E
r
r
rrrr
r
r
r
r
r
r
r
r
r
r
r
r
r
r
ε
,
(2.11-11)
где
.;
2
1
2
1
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
u
nu
u
u
u
xn
x
x
x
q
q
q
q
q
q
q
q
L
r
L
r
(2.11-12)
Обозначив
u
T
uXUu
T
uUx
T
xX
qqQqqQqqQ
r
r
rrrr
=
== ;; , (2.11-13)
в итоге получаем критерий (2.11-4).
В связи с тем, что порядки уравнений объекта и эталонной систе-
мы совпадают, в результате оптимального синтеза удастся найти опти-
мальное управление, при котором минимум функционала окажется рав-
ным нулю. Так как при этом для процессов в системе с оптимальным
управлением окажется выполнимым равенство (2.11-6) при
0=
E
ε
, то
полученная система будет иметь характеристический полином
nn
nn
ЭC
γ
λ
γ
λ
γ
λ
λ
ϕ
λ
ϕ
+
+
+
+==
−
−
1
1
1
...)()( (2.11-14)
и, следовательно, собственные числа синтезированной системы совпа-
дут с собственными числами эталона.
Таким образом, результаты АКР при таком подходе обеспечивают
не только минимум критерия (2.11-4), равный нулю, но и позволяет по-
лучить систему с желаемыми собственными числами. Поскольку связь
переходных процессов с собственными числами (модами) системы бо-
лее очевидна и непосредственна
, модальный синтез часто оказывается
предпочтительнее метода АКР, тем более, что алгоритм модального
синтеза существенно проще алгоритмов АКР.
ПРИМЕР 1
. Для иллюстрации изложенного рассмотрим объект,
представленный на рис. 2.9. Уравнения объекта имеют вид:
.)()()(
);()(2)(
);()(
33
322
21
tutxtx
txtxtx
txtx
+−=
+−=
=
&
&
&
(2.11-15)
123
Пусть эталонная система (эталонный процесс) определяется уравнени-
ем
)()()()(
33
)1(
2
)2(
1
)3(
tvtxxtxtx
ЭЭЭЭ
γ
γ
γ
γ
=
+
++ , (2.11-16)
соответствующим желаемым собственным числам. Из этого уравнения
видно, что при постоянном командном сигнале constvv
=
=
0
в статике
0
))((lim vxtx
устЭЭ
t
=
=
∞→
. (2.11-17)
Подставив в левую часть равенства (2.11-16) координату объекта
)(
1
tx и
получим уравнение невязки:
)()()()()(
13
)1(
12
)2(
11
)3(
1
txtxtxtxt
E
γ
γ
γ
ε
+
+
+= . (2.11-18)
Заменим производные от координаты
1
x на координаты вектора состоя-
ния объекта с учётом уравнений (2.11-15):
.342
;2
;
32
)1(
3
)1(
2
)3(
1
31
)1(
2
)2(
1
2
)1(
1
uxxxxx
xxxx
xx
+−=+−=
+−==
=
(2.11-19)
В результате уравнение невязки принимает вид
)()()3()()24()()(
3122113
tutxtxtxt
E
+
−
+
+−+=
γ
γ
γ
γ
ε
, (2.11-20)
откуда получаем:
1;
3
24
1
21
3
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+−=
ux
qq
γ
γγ
γ
r
. (2.11-21)
Теперь в соответствии с (2.11-13) могут быть вычислены матрицы
X
Q ,
U
Q ,
XU
Q и получен функционал (2.11-4) для использования при решении
задачи АКР.
В то же время, приравняв нулю
)(t
E
ε
в (2.11-20), можно непосред-
ственно получить выражение для формирования управления
)(tu через
координаты вектора состояния объекта. Более того, если потребовать
выполнения равенства
)()()()()(
313
)1(
12
)2(
11
)3(
1
tvtxtxtxtx
γ
γ
γ
γ
=
+
++ , (2.11-22)
то с учётом (2.11-20) получим систему с обратной связью по вектору со-
стояния и управлением
)()()( tvktxLtu
v
+=
r
, (2.11-23)
124
где фигурируют матрица обратной связи
[]
1213
324
γ
γ
γ
γ
−
−
+−−=L (2.11-24)
и передаточный коэффициент по командному сигналу
3
γ
=
v
k . (2.11-25)
Таким образом, без решения задачи АКР получено оптимальное
управление, обеспечивающее процессы в замкнутой системе, имеющей
собственные числа, соответствующие характеристическому полиному
эталонной системы (2.11-14). Кроме того, в полученной системе обеспе-
чена единичная статика по командному сигналу
v
(2.11-17).
В этом примере проиллюстрирована идентичность задачи АКР с надле-
жащим образом выбранным критерием оптимальности задаче модаль-
ного синтеза. В следующих разделах будет подробно изложена методи-
ка модального синтеза.
125
3. Синтез линейных непрерывных систем
3.1. Выбор корректирующих звеньев. Метод желаемых ЛЧХ
Как уже отмечалось, существует связь между частотными характе-
ристиками системы, как в замкнутом, так и в разомкнутом состоянии, и
протекающими в ней переходными процессами. На протяжении многих
лет инженерами накоплен большой опыт по синтезу систем автоматиче-
ского управления на базе формирования эталонных, желаемых частот-
ных характеристик соответствующих разомкнутых систем. В
литературе
имеются обширные таблицы таких эталонных логарифмических ампли-
тудно-частотных характеристик для большого числа типовых передаточ-
ных функций объектов управления. В настоящем пособии излагается
лишь основная идея такого подхода.
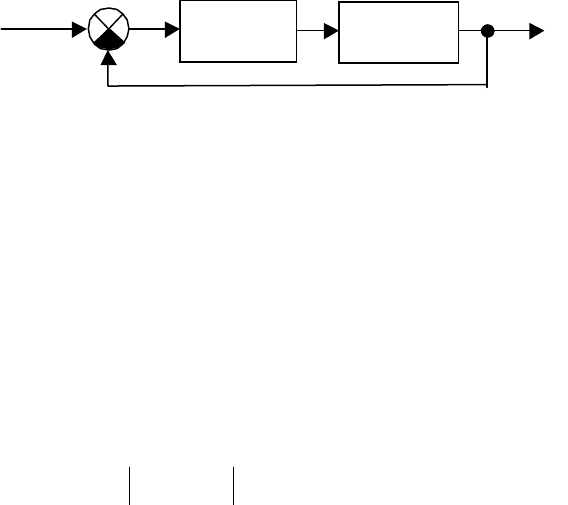
Рассматривается одноконтурная система (рис. 3.1). Разомкнутый
контур состоит из последовательно включённых неизменяемой части
системы (в неё входят объект, привод, датчики, преобразующие и согла
-
сующие устройства) с передаточной функцией
)(
0
pW
и корректирую-
щее звено с передаточной функцией
)(pW
k
.
Рис. 3.1. Исходная структурная схема
)( pW
k
)(
0
pW
y
v
Предполагается, что заданы требования к основным показателям
качества, обсуждавшимся в п.2.10.1. В соответствии с этим по упомяну-
тым таблицам, или на основе подхода, изложенного в п.2.10.4, строится
асимптотическая логарифмическая амплитудно-частотная характери-
стика (ЛАЧХ)
)(
ω
жел
L разомкнутой системы, удовлетворяющая указан-
ным требованиям. На этом же рисунке строится асимптотическая ЛАЧХ
неизменяемой части системы
дБ
jWL )()(
00
ω
ω
= . (3.1-1)
Потребуем, чтобы комплексный передаточный коэффициент ра-
зомкнутой системы был равен функции, определяемой желаемой ЛАЧХ,
то есть
)()()(
0
ω
ω
ω
jjjW
W
W
k
жел
= (3.1-2)

126
или
)()()(
0
ω
ω
ω
LLL
kжел
+
= . (3.1-3)
В соответствии с этим простой операцией графического вычитания легко
получить асимптотическую ЛАЧХ корректирующего звена
)()()(
0
ω
ω
ω
LLL
желk
−
= . (3.1-4)
По ней уже нетрудно восстановить передаточную функцию
)(pW
k
.
ПРИМЕР 3.1-1
. Передаточная функция неизменяемой части сис-
темы
)11.0)(1(
1
)(
0
++
=
ppp
p
W
.
Требования к системе
.
1) При отработке командных сигналов, меняющихся со скоростью до
10ед/с, ошибка не должна превосходить 0.1 ед..
2) Время регулирования
≈
р
t 1с.
3) Ошибка воспроизведения гармонических сигналов с амплитудой
v
A
на частотах до 1рад/c должна быть не более 0.05
v
A .
Последовательность расчёта
.
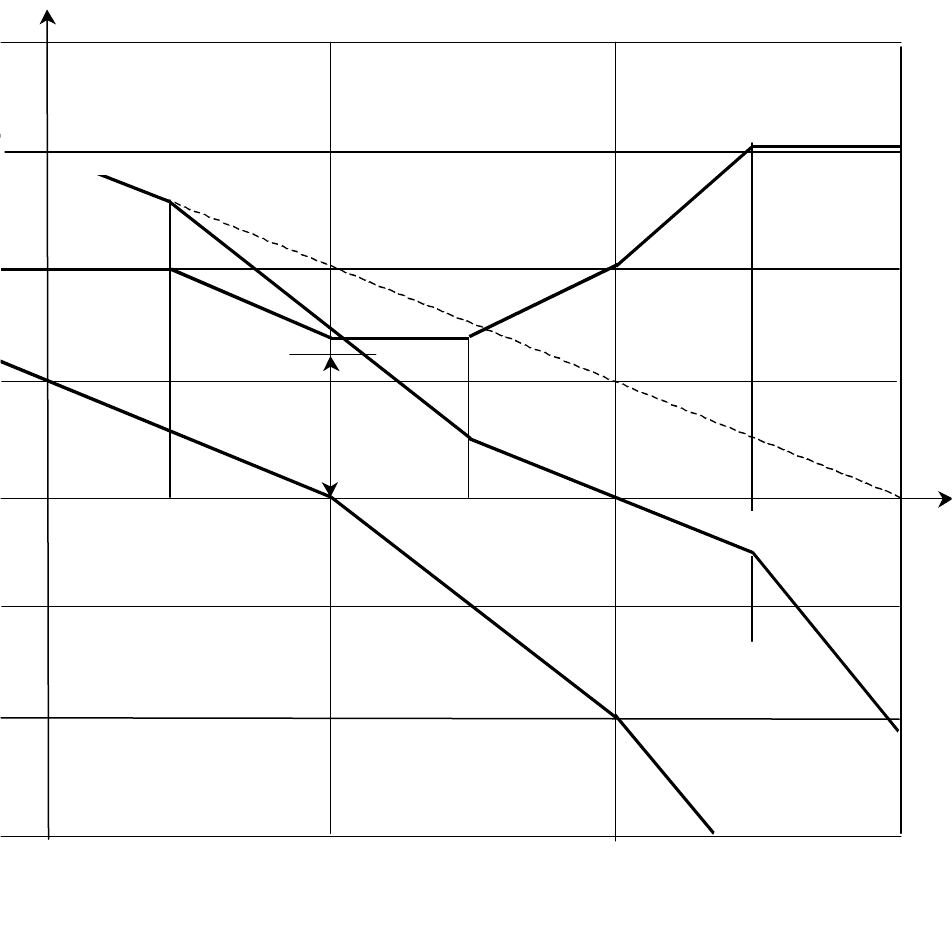
1. Построить асимптотическую ЛАЧХ неизменяемой части системы
)(
0
ω
L (рис. 3.2).
2. Построить желаемую ЛАЧХ
)(
ω
жел
L .
В связи с тем, что согласно п.1 требований к системе при линейно
изменяющемся во времени командном сигнале допустима постоянная
ошибка, система должна иметь астатизм первого порядка. Поэтому
низкочастотная асимптота должна идти с наклоном -20 дБ/дек. В со-
ответствии с (2.10-22) добротность системы
c
v
K
ед
cед
1
][
]/[
1
100
1.0
10
)(
−
==
∞
=
ε
.
Следовательно, низкочастотная асимптота должна пересекать ось
частот при
100=
ω
рад/с.
Частота среза определяется с учётом требуемого времени регули-
рования из (2.10-34):
cрад
t
р
c
/10
)43(
≈
÷
=
π
ω
.
Таким образом, среднечастотный участок желаемой ЛАЧХ на этой
частоте пересекает ось абсцисс, имеет наклон -20 дБ/дек имеет
протяжённость, равную одной декаде, то есть занимает интервал
127
6.3116.3 ≤≤
ω
.
Диапазон частот
6.31>
ω
считаем высокочастотным. Наклон
высокочастотной асимптоты выбираем равным -60 дБ/дек, - та-
ким же, как наклон высокочастотной асимптоты неизменяемой
части системы.
Для того, чтобы упростить реализацию корректирующего звена,
низкочастотную и среднечастотные асимптоты соединяем от-
резком прямой с наклоном -40 дБ/дек. При этом следует учесть
требование по точности воспроизведения гармонического сиг-
нала:
в соответствии с (2.10-33) на частоте 1 рад/c желаемая
ЛАЧХ должна пройти выше уровня 26 дБ.
][дБ
L
ω
-60
-40
-20
40
60
жел
L
k
L
k
L
26 дБ
+40 дБ/дек
-20 дБ/дек
0
L
-60 дБ/дек
-40 дБ/дек
-20 дБ/дек
20
100
10
1
0.1
0.33
3.16
31.6
Рис. 3.2. Иллюстрация к методу желаемых ЛЧХ
3. Построить ЛАЧХ корректирующего звена, производя графическое вы-
читание отрезков прямых в соответствии с (3.1-4).

128
4. Замерить значения сопрягающих частот асимптотической ЛАЧХ кор-
ректирующего звена и записать соответствующее выражение для пе-
редаточной функции
2
)1
6.31
1
)(1
33.0
1
(
)1
10
1
)(1
16.3
1
)(1(100
)(
++
+++
=
pp
ppp
pW
k
.
3.2. Управляемость линейных стационарных систем
Непрерывная линейная система
)()()( tuBtxAtx
r
r
&
r
+= (3.2-1)
является полностью управляемой тогда и только тогда, когда она может
быть переведена из любого начального состояния
)(
0
tx
r
в произвольный
момент времени
0
t в любое конечное состояние
)(
1
tx
r
за конечное время
01
tt − .
Примем начальные условия нулевыми:
0)(
0
=
tx
r
. Тогда, в соответ-
ствии с формулой Коши
∫
−
=
t
t
duBtx
e
tA
1
0
1
)()(
)(
1
ττ
τ
rr
. (3.2-2)
Принимая во внимание выражение для матричной экспоненты в
виде бесконечного ряда
...
!2
)(
!1
)(
2
1
2
1
)(
1
+
−
+
−
+=
−
τ
τ
τ
tAtA
Ee
tA
, (3.2-3)
равенство (3.2-2) можно записать в виде
()
()
...)(
!2
)()()(
1
0
1
0
1
0
2
1
2
11
+
−
+−+=
∫∫∫
ττ
τ
ττττ
du
t
BAdtutABduBtx
t
t
t
t
t
t
rrrr
Обозначим:
()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
−
=
∫
i
ni
i
i
t
t
i
du
i
t
,
2
1
2
1
...
)(
!
1
0
α
α
α
ττ
τ
α
r
r
. (3.2-4)

129
Представим произведения
B
A
i
в виде блочных матриц векторов
β
r
:
⎥
⎦
⎤
⎢
⎣
⎡
=
n
iii
i
BA
βββ
r
rr
...
21
. (3.2-5)
Тогда
()
[
]
ν
ν
ν
βαβββττ
τ
i
nu
iiii
t
t
i
i
nu
du
i
t
BA
rrrr
r
∑
∫
=
==
−
1
1
...)(
!
21
1
0
(3.2-6)
и
∑∑
∞
==
⋅=
01
1
)(
i
nu
ii
tx
ν
νν
βα
r
r
. (3.2-7)
В результате вектор
)(
1
tx
r
может рассматриваться как линейная
комбинация векторов
ν
β
i
r
, являющихся вектор-столбцами матриц
...,,,,
32
BABAABB . Иначе говоря, конечное состояние )(
1
tx
r
принад-
лежит линейному подпространству, порождаемому вектор-столбцами
бесконечной последовательностью матриц
...,,,,
32
BABAABB .
В этой последовательности должна появиться матрица
B
A
l
, все
вектор-столбцы которой линейно зависят от вектор-столбцов предыду-
щих матриц
.,...,,,
12
BABAABB
l −
Такая матрица обязательно должна
иметь место, так как в линейном n-мерном пространстве не может быть
более чем
n линейно–независимых векторов. Отсюда же следует, что
nl ≤ .
Таким образом, можно записать
1
1
10
...
−
−
Λ
+
+Λ+Λ=
l
ll
BAABBBA , (3.2-8)
где
i
Λ
- соответствующие диагональные матричные коэффициенты
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅⋅
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
⋅⋅⋅
⋅⋅⋅
=Λ
in
i
i
i
λ
λ
λ
00
00
00
2
1
. (3.2-9)
Очевидно, тем же свойством обладает и матрица
B
A
l 1+
, так как
12
1
1
2
0
1
...
−−
−+
Λ
+
Λ
+
+
Λ
+Λ
=
=
l
l
l
lll
BABABAABAABA . (3.2-10)
По индукции можно утверждать то же самое и для всех
B
A
k
при lk ≥ .

130
Итак, конечное состояние
)(
1
tx
r
принадлежит линейному подпро-
странству, порождаемому вектор-столбцами матриц
,,,
2
BAABB ... , BA
n 1−
(здесь учтено, что
nl ≤ ). Если эти вектор-столбцы не порождают n -
мерное пространство, то в такой системе можно достичь лишь тех со-
стояний, которые принадлежат подпространству меньшей размерности.
Таким образом, критерий управляемости формулируется следую-
щим образом:
Система
(
)()
(
)
tuBtxAtx
r
r
&
r
+= полностью управляема тогда и
только тогда, когда ранг матрицы управляемости
][
12
BABAABBU
n−
= L (3.2-11)
равен
n , то есть полной размерности линейного пространства. При
этом говорят, что пара матриц {A, B} полностью управляема.
ПРИМЕР 3.2-1
. Определить управляемость системы
.
;323
;554
1
212
211
xy
Uxxx
Uxxx
=
+−=
−
+−=
&
&
Для этой системы
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
3
5
,
23
54
BA
и матрица управляемости
[]
⎥
⎦
⎤
⎢
⎣
⎡
−
−
==
213
355
ABAU .
Определитель этой матрицы равен нулю, она имеет ранг меньше двух,
то есть порядка системы, и система является неуправляемой.
Отметим, что собственные числа матрицы динамики системы
7;1
21
−
=
+
=
λ
λ
,
то есть система неустойчива. В тоже время передаточная функция по
выходной координате
,
7
5
)(
+
−=
p
pW
uy
