Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

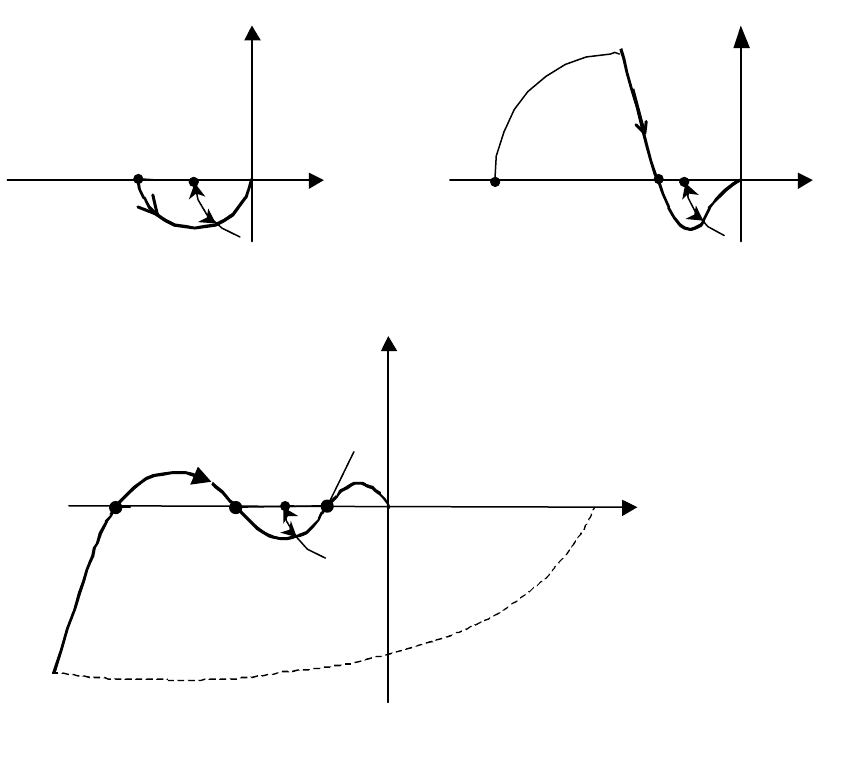
101
дов расширенной амплитудно-фазовой характеристикой участка веще-
ственной оси
),1( ∞
−
− .
Переходом называется пересечение амплитудно-фазовой ха-
рактеристикой вещественной оси на интервале
]1,( −
−
∞ . Переход
считается положительным, если при увеличении частоты в точке
перехода фаза растет, и отрицательным, – если уменьшается. Если
амплитудно-фазовая характеристика начинается, или заканчивается
на указанном участке вещественной оси, то имеет место половина
перехода с соответствующим знаком.
На рис. 2.43 приведены примеры, иллюстрирующие понятие пере-
ходов и критерий Найквиста. Все три примера
соответствуют системам,
устойчивым в замкнутом состоянии.
Рис 2.43. Иллюстрация к анализу устойчивости
з
ϕ
з
ϕ
з
ϕ
B
A
A
A
o
o
o
)(
3
ω
j
W
)(
2
ω
jW
)(
1
ω
jW
-0.5п
+
0.5п 1,0
j
+
-1
,
j
0
+1п
0п-1п
+j
+1п
-1,0
j
+j
+
+j
+
m=0
m=1
m=1
В системе координат логарифмических частотных характеристик
переход имеет место, если фазочастотная характеристика пересекает
линию
π
π
k±− (к=1,2...), и при этом логарифмическая амплитудно-
частотная характеристика идет выше оси абсцисс (модуль комплексного
передаточного коэффициента больше единицы).
102
Приведем теперь формулировку критерия Найквиста, использую-
щую понятие переходов.
Если передаточная функция разомкнутой системы имеет
m
полюсов с положительной вещественной частью, то для устойчиво-
сти системы в замкнутом состоянии необходимо и достаточно, что-
бы суммарное число переходов расширенной логарифмической час-
тотной характеристики было равно
2
/
m
+
. Если замкнутая систе-
ма неустойчива, то число ее «неустойчивых» полюсов
∑
Π
−= 2mz , (2.9-50)
где
∑
Π – суммарное число переходов расширенной частотной ха-
рактеристики разомкнутой системы.
2.9.4.4. Понятие запасов устойчивости
Естественно, что каждая система автоматического управления
должна быть устойчивой. В инженерной практике часто используется
понятие запасов. Например в строительстве и машиностроении обще-
принятым является термин "запас прочности". Аналогично этому при
проектировании систем управления пользуются понятиями запасов ус-
тойчивости.
Запасом устойчивости по модулю будем называть число, большее
единицы, которое показывает, во сколько раз (на сколько децибел) нуж-
но изменить исходный передаточный коэффициент разомкнутой систе-
мы, чтобы вывести замкнутую систему на границу устойчивости. Соот-
ветственно различают запасы по модулю на увеличение и уменьшение
коэффициента. На рис. 2.43 для каждого из вариантов
длина отрезка oA
численно равна запасу устойчивости по модулю на уменьшение; вели-
чина, обратная длине отрезка
oB для третьего варианта - запасу устой-
чивости по модулю на увеличение.
Запасом устойчивости по фазе
з
ϕ
называют минимальный по мо-
дулю угол, на который следует довернуть вектор
)(
ω
j
W с модулем,
равным единице, чтобы его конец оказался в точке
)0,1(
j
− . На рис.
2.43 для каждого из вариантов АФХ указан запас устойчивости по фазе.
2.9.4.5. Устойчивость систем с запаздыванием
Звено транспортного запаздывания смещает по времени выходной
сигнал относительно входного на величину запаздывания
τ
:
)()(
τ
−= tut
y
. (2.9-51)
Передаточная функция и комплексный передаточный коэффициент со-
ответственно представлены выражениями (2.9-52) и (2.9-53):
p
з
epW
τ
−
=)( ; (2.9-52)
ωτ
ω
j
з
ejW
−
=)( . (2.9-53)

103
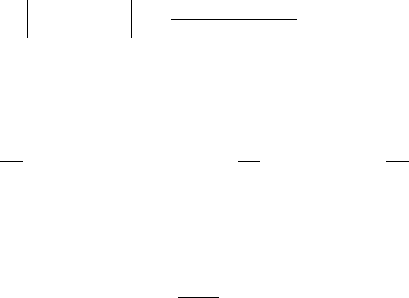
При исследовании устойчивости системы, в которую входит звено
запаздывания, приводят её структурную схему к виду (рис. 2.44), в кото-
ром это звено оказывается включённым последовательно с остальной
частью системы
Рис. 2.44. Типовая структура системы
с запаздыванием
y
v
)(pW
з
)(
0
pW
При этом, если обозначить
)(
)(
)(
0
0
0
pQ
pR
pW =
,
то характеристическое уравнение замкнутой системы примет вид
0)()(
00
=
+
−
τ
p
epRpQ . (2.9-54)
В связи с тем, что разложение в ряд Тейлора экспоненциальной функ-
ции имеет вид
...)(
!3
1
)(
!2
1
1
1
32
+−+−
=
−
τττ
τ
ppp
e
p
,
то характеристическое уравнение (2.9-54) имеет бесконечно большое
число корней. При этом, естественно, алгебраические критерии устойчи-
вости неприменимы. В то же время, для данной системы может быть ис-
пользован критерий Найквиста.
ПРИМЕР 2.9-2.
Пусть структурная схема системы с запаздыванием
приведена к виду, представленному на рис. 2.44 и
2
0
)1(
2
)(
+
=
Tp
pW
.
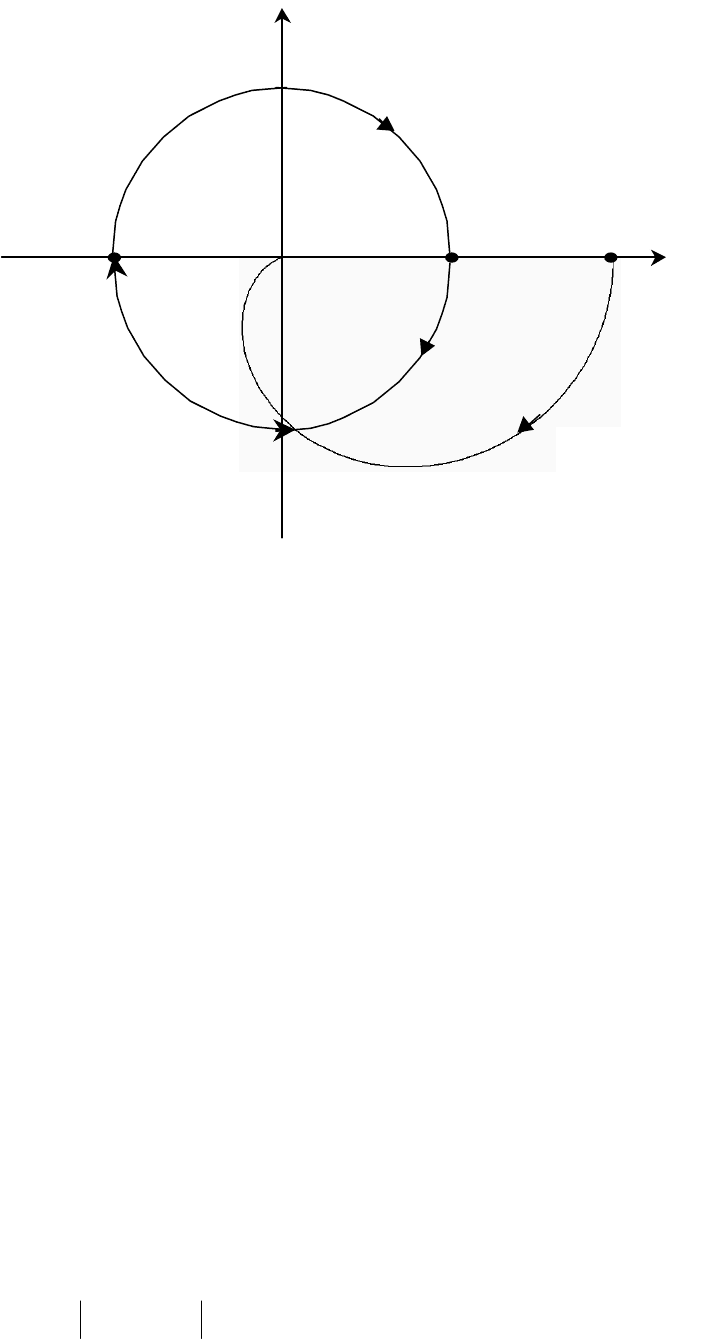
На рис. 2.45 представлены амплитудно-фазовые характеристики
звена запаздывания и последовательно с ним включённого звена
)(
0
ω
jW .
104
1−
1
2
)(
0
ω
jW
ωτ
j
e
−
ϕ
Δ
Рис. 2.45. Исследование устойчивости системы
с запаздыванием
j
+
+
Так как модуль комплексного передаточного коэффициента звена за-
паздывания на всех частотах равен единице, то АФХ разомкнутой сис-
темы
ωτ
ω
ω
j
ejWjW
−
= )()(
0
(2.9-55)
отличается от
)(
0
ω
jW только фазой:
ωτ
ω
ϕ
ω
ϕ
−
= )()(
0
. (2.9-56)
Если провести дугу окружности единичного радиуса с центром в начале
координат от отрицательной вещественной полуоси до пересечения с
АФХ
)(
0
ω
jW в точке
'1'
ω
ω
= , то полученное значение
ϕ
Δ из соотно-
шения
кр
τ
ω
ϕ
⋅
=
Δ
'1'
(2.9-57)
позволит найти так называемое критическое время запаздывания
кр
τ
,
то есть время запаздывания, при котором система выводится на границу
устойчивости. Здесь
'1'
ω
- значение частоты, при которой
1)(
'1'0
=
ω
jW . (2.9-58)
В рассматриваемом примере
105
2
0
)(1
2
)(
T
jW
ω
ω
+
=
, (2.9-59)
откуда
T
1
'1'
=
ω
,
2
)(
"1"0
π
ωϕ
−= ,
2
π
ϕ
=Δ (2.9-60)
и
2
T
кр
π
τ
= . (2.9-61)
2.10. Качество процессов управления
2.10.1. Основные показатели качества
Устойчивость - это необходимое, но недостаточное условие эф-
фективной работы системы.
Комплекс требований, определяющих поведение системы в уста-
новившихся и переходных процессах отработки заданного воздействия,
определяется понятием «качество процесса управления» или качество
системы.
На этапе разработки системы управления рассматривают процес-
сы управления в устойчивых системах при воздействии особо "тяжелых"
для них
сигналов, заданных в виде определенных или случайных функ-
ций времени
Качество работы системы проверяется по ее реакции на:
1) дельта функцию
)(
t
δ
;
2) единичную функцию
)(1 t ;
3) гармонический сигнал
tA
H
ω
sin⋅ ;
4) случайные воздействия с заданными вероятностными характеристи-
ками.
Качество отработки типовых сигналов оценивают либо непосред-
ственно по выходному сигналу
)(t
y
, либо путем сравнения этого сигна-
ла
)(ty с реакцией некоторой эталонной системы (рассогласование
)(t
e
ε
на рис.2.46), либо по ошибке воспроизведения командного сигнала
)()()( tytvt
v
−=
ε
.
106
)(ty
e
)(
t
y
)(t
e
ε
)(
t
v
Управляемая
система
Эталонная
система
Рис. 2.46. Сравнение управляемой
системы с эталонной
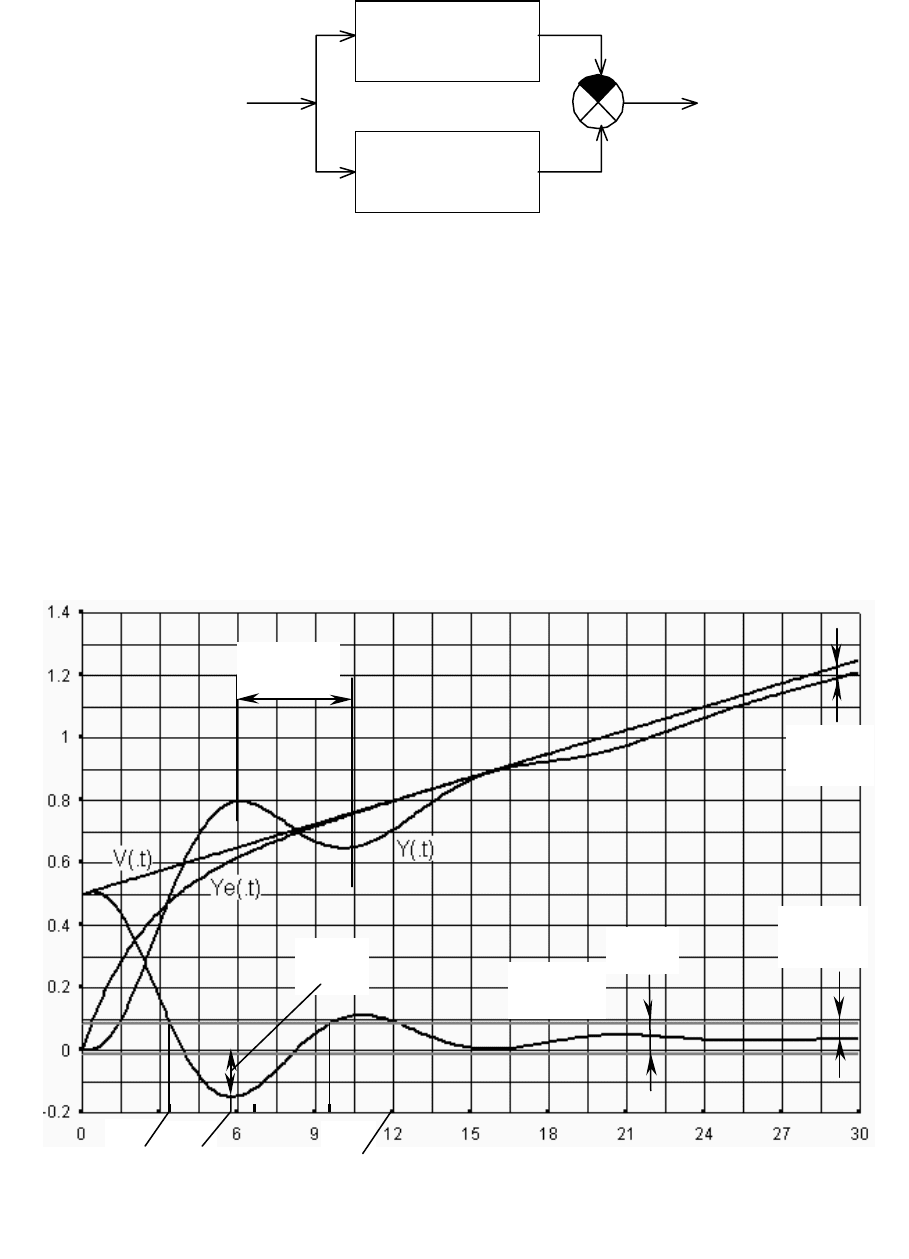
На рис. 2.47 представлена реакция некоторой следящей системы
на линейно возрастающий командный сигнал
)(1)025.05.0()( tttv += ,
на рис. 2.48 – реакция на единичную функцию.
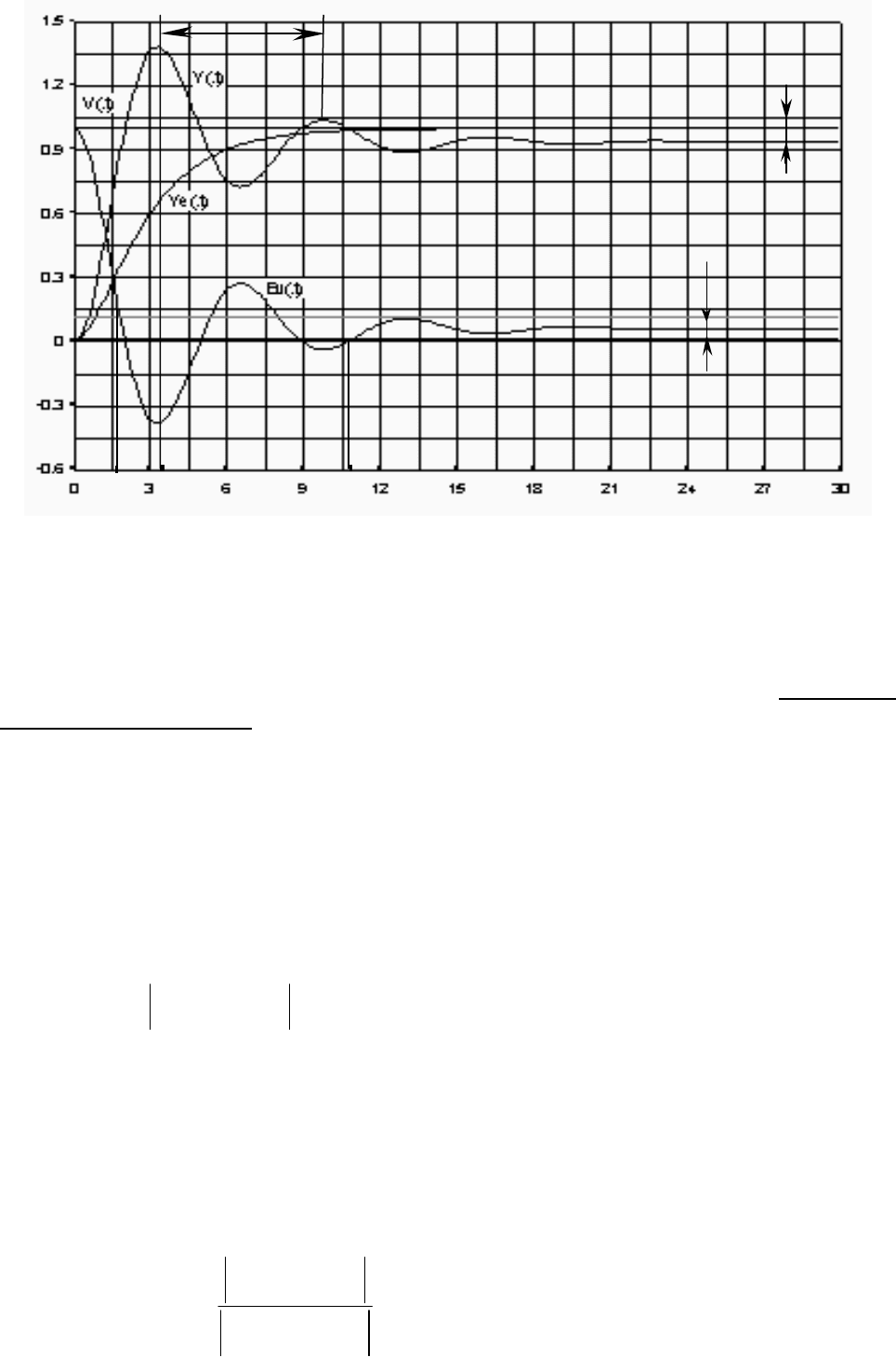
Рис. 2.47. Иллюстрация к характеристикам качества системы
(реакция на линейно изменяющийся сигнал)
2/
k
T
vm
ε
Δ
2
vуст
ε
vуст
ε
н
t
р
t
м
t
)(t
v
ε
107
Рис. 2.48. Иллюстрация к определению показателей качества
(реакция на единичную функцию)
k
T
Δ
2
vуст
E
н
t
р
t
м
t
С помощью этих рисунков удобно проиллюстрировать основные
показатели качества, используемуе при анализе систем управления.
1. Установившаяся ошибка:
))()((lim)( tytv
t
уст
−
=∞=
∞→
ε
ε
. (2.10-1)
2. Время регулирования
р
t - минимальное время, в течение которого
переходный процесс перестает выходить за пределы заданной
«трубки». Определяется из условия
Δ≤−
уст
t
εε
)(
при
p
tt ≥ , (2.10-2)
где Δ - заранее заданное значение, определяемое требованиями к
точности системы (обычно 2-5% от значения командного или выход-
ного сигнала в установившемся режиме).
3. Максимальное перерегулирование σ - наибольший выброс управляе-
мого процесса относительно установившегося значения по отноше-
нию к разности
уст
ε
и )0(
ε
.
⋅
−
−
= %100
)0(
εε
εε
σ
уст
устмах
(2.10-3)
108
Обычно требуют
%4030
÷
≤
σ
.
4. Время нарастания:
н
t - время первого входа процесса в трубку.
5. Время максимального перерегулирования:
m
t .
6. Число перерегулирований
N
в интервале:
p
tt
≤
≤
0 -
число выбросов, для которых
Δ>−
mуст
εε
.
7. Частота или период
k
T колебательной составляющей переходного
процесса.
2.10.2. Ошибки системы регулирования в установившихся режи-
мах. Статические и астатические системы
Рассмотрим одну из самых распространённых структурных схем -
схему типа следящей системы (рис.2.49), назначение которой с мини-
мальной ошибкой воспроизвести на выходе
)(t
y
командный сигнал
)(tv .
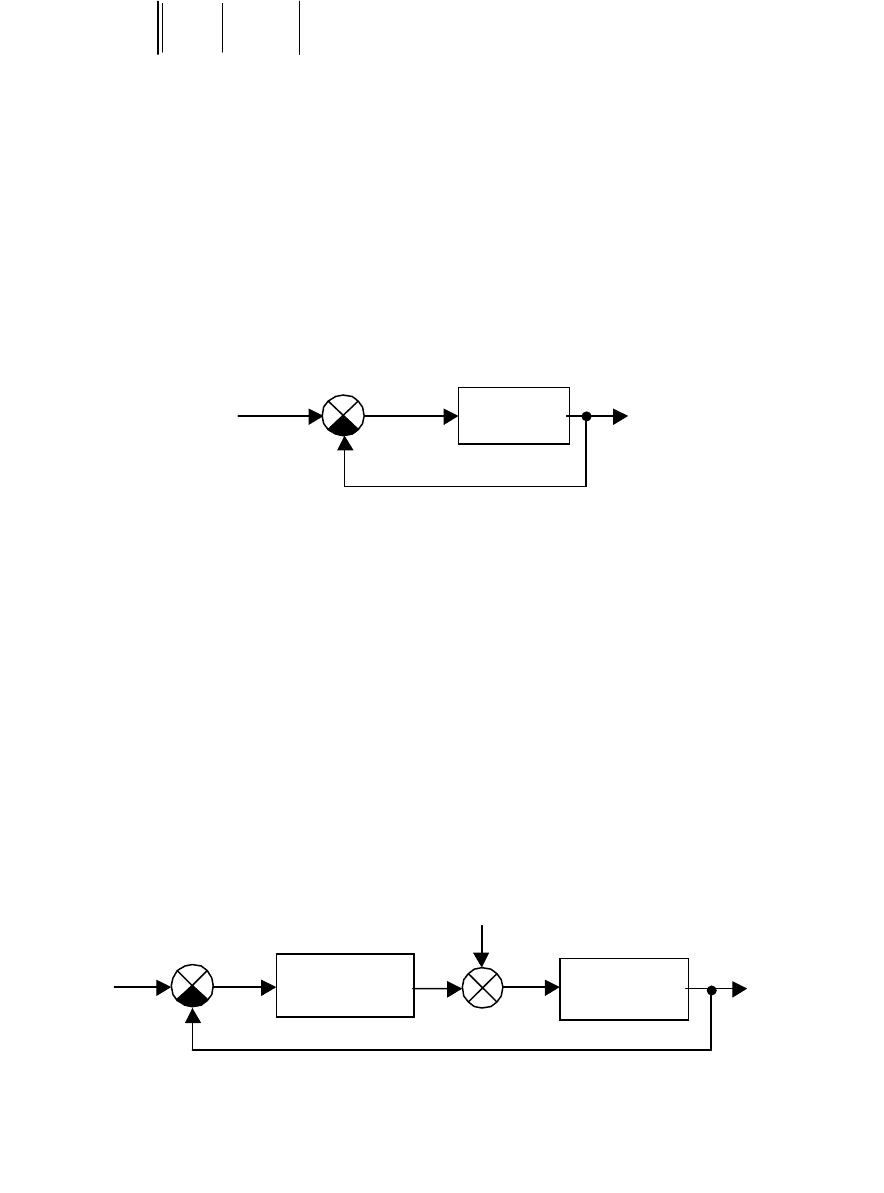
Рис.2.49. Простейшая типовая структура
следящей системы
)(
p
W
v
ε
y
В общем случае разомкнутая система может быть представлена
последовательным соединением объекта (неизменяемой части систе-
мы) с передаточной функцией
)(pW
об
и регулятора (корректирующего
звена) с передаточной функцией
)(pW
рег
. Кроме того, учтем дополни-
тельно возмущающее воздействие
)(tf . С учетом этого передаточная
функция разомкнутой системы
)()()( pWpWpW
обрег
=
, а исходная
структурная схема примет вид, представленный на рис.2.50.
Рис.2.50. Структурная схема системы для анализа точности
в установившихся режимах
)(pW
об
f
ε
v
y
)(pW
pег

109
В соответствии с этой структурной схемой изображение по Лапласу
от ошибки
)(
p
E
зависит как от командного сигнала, так и от возмуще-
ния:
)()()()()()()( pEpEpFpWpVpWpE
fvfv
+
=
⋅
+⋅=
εε
, (2.10-4)
где
)(1
1
)(
pW
p
W
v
+
=
ε
, (2.10-5)
)(1
)(
)(
pW
pW
pW
об
f
+
−
=
ε
. (2.10-6)
Широкий класс командных сигналов и возмущающих воздействий может
быть представлен степенными функциями времени
)(1...)(
2
210
ttt
⋅
+
++
α
α
α
. (2.10-7)
Сначала рассмотрим реакцию системы на возмущающее воздей-
ствие, вида:
)(1
!
)( tt
f
tf ⋅⋅=
ν
ν
ν
, (2.10-8)
где
constf =
ν
и имеет размерность возмущения f , деленную на
ν
се
к
. Такая функция имеет ненулевые производные от нулевого до
ν
порядка и нулевые производные порядка выше, чем
ν
. Причем,
ν
ν
ftf =)(
)(
. (2.10-9)
Изображение по Лапласу возмущения (2.10-8) имеет вид
1
)(
+
=
ν
ν
p
f
pF
. (2.10-10)
Пусть
)(
)(
)(
pQ
pRK
pW
об
обоб
об
= , (2.10-11)
)(
)(
)(
1
pQp
pRK
pW
рег
l
регрег
рег
=
(2.10-12)
и
1)0()0()0()0(
1
=
=
==
регобрегоб
QQRR . (2.10-13)
Тогда изображение ошибки можно представить в виде:

110
1
1
)()()()(
)()(
)(
+
⋅
⋅⋅⋅+⋅⋅
⋅
⋅
⋅
−
=
ν
ν
p
f
pRpRKKpQppQ
pQppRK
рE
регобрегобрег
l
об
рег
l
обоб
f
.
(2.10-14)
В соответствии с предельной теоремой преобразования Лапласа,
если существует
∞→t
t)(lim
ε
, то
ν
ν
ε
−
→→∞→
⋅⋅
⋅
−
=⋅=
l
регоб
об
p
f
p
f
t
pf
KK
K
pEpt
00
lim)(lim)(lim . (2.10-15)
Если
l=
ν
, то
рег
f
t
K
f
t
ν
ε
−
=
∞→
)(lim . (2.10-16)
Очевидно, в этом случае размерность коэффициента
рег
K равна
отношению размерностей возмущения и ошибки, умноженному на
l
се
к
−
.
Такая система называется астатической по возмущающему воздейст-
вию с порядком астатизма
l . Если на вход такой системы подать воз-
мущающий сигнал типа степенной функции времени с
l<
ν
, то устано-
вившаяся ошибка будет равна нулю.
Если
0=l , то нетрудно убедится в том, что если возмущение яв-
ляется единичной функцией:
)(1)(
0
tftf ⋅= , (2.10-17)
то
0
1
)( f
KK
K
регоб
об
f
⋅
⋅+
−
=∞
ε
. (2.10-18)
Такая система называется статической, поскольку при постоянном
возмущении ошибка в статике не равна нулю, пропорциональна величи-
не возмущения
0
f и тем меньше, чем больше коэффициент усиления ра-
зомкнутого контура
регоб
KKK = .
Аналогичные рассуждения можно провести для случая, когда
0=f , а командный сигнал является степенной функцией времени:
ν
ν
ν
t
v
tv ⋅=
!
)( . (2.10-19)
В этом случае положим
)()()()(
1
pQppQpQpQ
l
регоб
⋅
=
⋅= и 1)0(
1
=
Q . (2.10-20)
