Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.


91
0
21
2
2
0
=+⋅+⋅ ya
dt
dy
a
dt
yd
a
,
характеристическое уравнение
0
10
2
0
=
++ aaa
λ
λ
и матрицу Гурвица
⎥
⎦
⎤
⎢
⎣
⎡
=
20
1
0
aa
a
G
.
Как и в предыдущем случае, при
0
0
>a применение критерия Гурви-
ца даёт тривиальный результат:
0 ,0
21
>> aa .
Отметим, что для систем первого и второго порядка необходимое
условие устойчивости является и достаточным.
•
3=n .
Запишем характеристическое уравнение
0
32
2
1
3
0
=
+
+
+
aaaa
λ
λ
λ
и матрицу Гурвица
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
31
20
31
0
0
0
aa
aa
aa
G
.
Для устойчивости системы по критерию Гурвица необходимо и дос-
таточно, чтобы при
0
0
>a были положительны первый
0
11
>=Δ a ,
второй
0
3021
20
31
2
>−==Δ aaaa
aa
aa
и третий
0
0
0
0
23
31
20
31
3
>Δ==Δ a
aa
aa
aa

92
главные миноры матрицы Гурвица. С учётом необходимого условия
устойчивости (требования положительности всех коэффициентов ха-
рактеристического уравнения) критерий Гурвица для устойчивости
системы третьего порядка требует выполнения неравенства
0
3021
>− aaaa . (2.9-19)
•
4=n .
Запишем характеристическое уравнение
0
43
2
2
3
1
4
0
=
+
+++ aaaaa
λ
λ
λ
λ
и матрицу Гурвица
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
420
31
420
31
0
00
0
00
aaa
aa
aaa
aa
G
.
Для устойчивости системы по критерию Гурвица необходимо и дос-
таточно, чтобы при
0
0
>a были положительны первый
0
11
>=Δ a ,
второй
0
3021
20
31
2
>−==Δ aaaa
aa
aa
,
третий
0)(
0
0
2
1430213
31
420
31
3
>−−==Δ aaaaaaa
aa
aaa
aa
и четвёртый
0
344
>Δ=
Δ
a
главные миноры матрицы Гурвица. С учётом необходимого условия
устойчивости (требования положительности всех коэффициентов ха-
рактеристического уравнения) критерий Гурвица для устойчивости
системы четвёртого порядка требует выполнения неравенства
0)(
2
1430213
>−− aaaaaaa . (2.9-20)
Для системы пятого порядка критерий Гурвица выливается в тре-
бование выполнения уже двух неравенств:
93
.0)())((
0
2
504152433021
3021
>−−−−
>−
aaaaaaaaaaaa
aaaa
(2.9-21)
С дальнейшим увеличением порядка систем использование критерия
Гурвица становится всё более громоздким и теряет смысл. Если возни-
кает необходимость привлечения вычислительной техники, то в наше
время стало проще непосредственное вычисление корней характери-
стического уравнения. Тем не менее, для систем третьего - четвёртого
порядков привлекает простота использования критерия Гурвица.
ПРИМЕР 2.9-1.
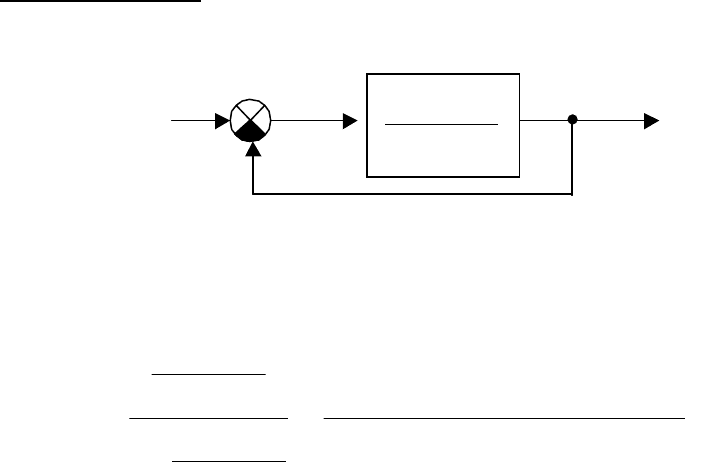
Рассмотрим систему, представленную на рис. 2.40,
с входным сигналом
v , сигналом ошибки
ε
, и выходным сигналом
y
.
Рис 2.40 Структурная схема системы
y
ε
v
3
)1( +Tp
k
Этой системе соответствует передаточная функция
kTppTpT
k
Tp
k
Tp
k
pW
vy
++++
=
+
+
+
=
133
)1(
1
)1(
)(
2233
3
3
.
В соответствии со свойствами передаточных функций характеристиче-
ский полином замкнутой системы имеет вид
kTppTpTp
+
+
+
+= 133)(
2233
ϕ
.
По критерию Гурвица система устойчива, если выполняется неравенст-
во
0)1(9
33
3021
>
+
−=− kTTaaaa .
Отсюда, с учётом требования положительности всех коэффициентов
характеристического полинома, следует, что система устойчива, если
при
0>T выполняются неравенства
81 <<− k .
Значения параметров, при которых система находится на границе
устойчивости, принято называть критическими. В данном примере у ко-
эффициента
k имеется два критических значения - нижнее 1
−
=
н
кр
k и
верхнее
8=
в
кр
k .
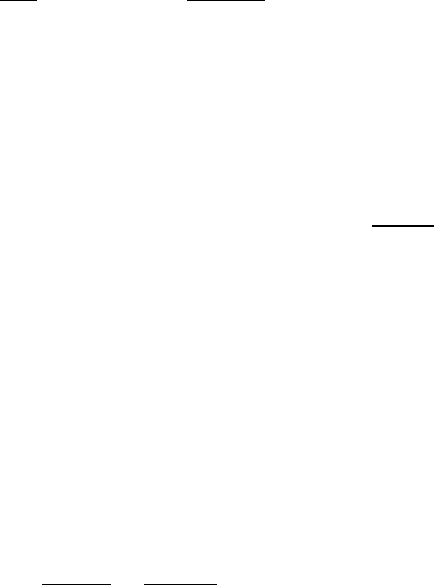
94
2.9.4. Частотный критерий устойчивости (критерий Найквиста)
Часто рассмотрению подлежат замкнутые системы, структурные
схемы которых могут быть приведены к типовому виду, представленно-
му на рис. 2.41. Как правило, передаточная функция разомкнутой систе-
мы
)(
p
W имеет относительно простой вид и несложно определить рас-
положение её полюсов относительно мнимой оси. Таким образом, пред-
полагается, что анализ устойчивости разомкнутой системы проведён. В
то же время, анализ устойчивости замкнутой системы представляет со-
бой нетривиальную задачу. Критерий устойчивости Найквиста оперирует
с частотными характеристиками, достаточно нагляден и позволяет ис-
пользовать
физические представления о свойствах исследуемой систе-
мы. Критерий Найквиста позволяет судить об устойчивости системы в
замкнутом состоянии по частотным характеристикам разомкнутой сис-
темы.
2.9.4.1. Понятие логарифмического вычета
Пусть задана некоторая функция
)(
p
Ψ
, аналитичная всюду в об-
ласти
G , за исключением конечного числа изолированных особых точек.
Будем полагать, что все особые точки являются полюсами. Будем пола-
гать также, что граница
C области G не содержит ни нулей, ни полюсов
функции
)(
p
Ψ .
Рассмотрим логарифмическую производную функции
)(
p
Ψ :
[]
)(
)(
)(ln)(
p
p
p
dp
d
p
Ψ
Ψ
′
=Ψ=L (2.9-22)
и назовем логарифмическим вычетом функции
)(
p
Ψ
в точке a
p
= вы-
чет в этой точке ее логарифмической производной:
{}
}),({Resa(p),LnRes apL=Ψ . (2.9-23)
Пусть функция
)(
p
Ψ имеет в точке a
p
=
ноль порядка k , то есть
)()()( pFapp
k
−=Ψ ,
где
0)( ≠a
F
.
Тогда
)()()()()(
1
pFappFapkp
kk
′
−
+
−
=Ψ
′
−
и
)(
)(
)(
pF
pF
ap
k
p
′
+
−
=L . (2.9-24)

95
Отметим, что полюсы функций
)(
p
F
и )(
p
F
′
совпадают. Так как нули
аналитической функции изолированы, то в достаточно малом круге
ρ
<− ap функция )()( pFpF
′
является аналитической и может быть
разложена в окрестности точки
a
p
=
в ряд Тейлора:
∑
∞
=
−=
′
0
)(
)(
)(
n
n
n
ap
pF
pF
α
.
С учётом этого (2.9-24) превращается в
∑
∞
=
−+
−
=
0
)()(
n
n
n
ap
ap
k
p
α
L .
Эта формула представляет собой разложение в ряд Лорана функции
)(
p
L в окрестности точки a
p
=
. Из этой формулы следует, что точка
a
p
= является полюсом первого порядка функции )(
p
L и
ka
p
=
}),({LRes . (2.9-25)
Пусть теперь функция
)(
p
Ψ
имеет в точке b
p
=
полюс кратности
s , то есть
)()()( pJbpp
s−
−=Ψ ,
где b не является ни нулём, ни полюсом функции )(
p
J
. Тогда
)()()()()(
)1(
pJbppJbpsp
ss
′
−
+
−−=Ψ
′
−+−
и
)(
)(
)(
pJ
pJ
bp
s
p
′
+
−
−
=L
.
По аналогии с предыдущим случаем получим, что в окрестности точки
b
p
=
∑
∞
=
−+
−
−
=
0
)()(
n
n
n
bp
bp
s
p
β
L ,
следовательно,
sb
p
−
=
}),({LRes . (2.9-26)
Таким образом, в нулях и полюсах функции
)(
p
Ψ
ее логарифми-
ческая производная (2.9-22)
)(
)(
)(
p
p
p
Ψ
Ψ
′
=L

96
имеет полюсы первого порядка, причем в нуле функции
)(
p
Ψ логариф-
мический вычет равен порядку нуля, а в полюсе – взятом со знаком ми-
нус порядку полюса.
По теореме вычетов имеем
∫
∑∑∑
−=
⎭
⎬
⎫
⎩
⎨
⎧
Ψ
Ψ
′
=
Ψ
Ψ
′
C
vv
v
v
vv
skp
p
p
dp
p
p
j
,
)(
)(
Res
)(
)(
2
1
π
,
или окончательно
Π−=
Ψ
Ψ
′
∫
Ndp
p
p
j
C
)(
)(
2
1
π
, (2.9-27)
где
N
– число нулей, а Π–число полюсов функции )(
p
Ψ
в области G.
2.9.4.2. Принцип приращения аргумента
Обозначим
)(
)()(
pj
epp
Ψ
Ψ=Ψ
ϕ
, (2.9-28)
тогда
)()(ln)(ln pjpp
Ψ
+
Ψ=Ψ
ϕ
. (2.9-29)
С учётом (2.9-27), получаем:
()
.)(
2
1
)(ln
2
1
)(ln
2
1
)(
)(
2
1
Π−=+Ψ=
=Ψ=
Ψ
Ψ
′
Ψ
∫∫
∫∫
Npdj
j
pd
j
pd
j
dp
p
p
j
CC
CC
ϕ
ππ
ππ
(2.9-30)
Поскольку в правой части равенства стоит вещественное число, то мни-
мая часть левой части равенства также равна нулю.
Таким образом, если функция
)(
p
Ψ
аналитична в замкнутой об-
ласти
G , ограниченной контуром C , за исключением конечного числа
полюсов в области
G , и если функция )(
p
Ψ
не имеет ни полюсов, ни
нулей на контуре
C , то приращение аргумента функции )(
p
Ψ при дви-
жении вектора
p
по замкнутому контуру C определяется выражением
)(2
Π
−
=Δ
Ψ
N
C
π
ϕ
. (2.9-31)
2.9.4.3. Анализ устойчивости замкнутой системы
Рассмотрим замкнутую систему с единичной обратной связью (рис.
2.41)

97
Рис 2.41. Замкнутая система с единичной
обратной связью
v
y
ε
)(
p
W
Пусть известно, что среди
n полюсов
n
ppp ,...,,
21
передаточной функ-
ции разомкнутой системы
)(
)(
)(
pQ
pR
pW =
(2.9-32)
имеется
1
v нулевых и
2
v чисто мнимых полюсов на верхней полуплоско-
сти плоскости комплексной переменной
p
(рис 2.42) , то есть
Рис 2.42. Расположение нулей ( ) и полюсов ( )
передаточной функции разомкнутой системы
j
+
+
G
C
C
)()()(
1
21
pQjpppQ
v
q
v
ω
−= . (2.9-33)
Образуем функцию
)(
)(
)(
)()(
)(1)(
pQ
pS
pQ
pRpQ
pWp =
+
=+=Ψ , (2.9-34)
характерную тем, что ее знаменатель является характеристическим по-
линомом разомкнутой системы, а числитель – характеристическим по-
линомом замкнутой.

98
Выберем в качестве области
G всю правую полуплоскость плос-
кости комплексной переменной
p
. Контур C сформируем из мнимой
оси, за исключением точек, совпадающих с полюсами передаточной
функции разомкнутой системы, дуг окружностей бесконечно малого ра-
диуса, охватывающих эти полюсы, как показано на рис. 2.42, и окружно-
сти бесконечно большого радиуса, охватывающей всю правую полу-
плоскость.
Допустим, в общем случае, что разомкнутая система неустойчива,
и её передаточная функция
имеет m "неустойчивых" полюсов, то есть
m полюсов в правой полуплоскости плоскости комплексной перемен-
ной
p
. Предположим, что замкнутая система также неустойчива, и
z
–
число неустойчивых полюсов передаточной функции замкнутой систе-
мы.
Тогда, в соответствии с принципом приращения аргумента
).(2 mz
c
−
=Δ
Ψ
π
ϕ
(2.9-35)
Если обходить контур
C в отрицательном направлении, совпадающим с
положительным направлением мнимой оси, то
)(2 zm
C
−
=Δ
−
Ψ
π
ϕ
. (2.9-36)
Будем сопоставлять изменение комплексной переменной р при пе-
ремещении ее вдоль контура C на плоскости
p
и соответствующее ему
изменение функции
)(
p
Ψ на комплексной плоскости Ψ . Для этого ра-
зобьем контур
C на несколько характерных участков.
На участке I годограф комплексной переменной
p
изменяется по
окружности бесконечно большого радиуса, охватывая всю правую полу-
плоскость, то есть
∞
→
=
Θ
ρ
ρ
,
j
I
ep . (2.9-37)
Ранее отмечалось, что в физически реализуемых системах порядок чис-
лителя передаточной функции не может превышать порядок ее знаме-
нателя. Отсюда следует, что степени полиномов
)(
p
S и )(
p
Q равны, а
значит
const
eQ
eS
p
j
j
==Ψ
Θ
Θ
∞→
)(
)(
lim)(
|
ρ
ρ
ρ
. (2.9-38)
Таким образом, приращение фазы функции
)(
p
Ψ
при изменении
p
вдоль первого участка равно нулю:
0=Δ
Ψ
I
ϕ
. (2.9-39)
В качестве участка II выберем мнимую ось плоскости
p
, то есть
ω
jp
II
= (2.9-40)

99
за исключением тех ее точек, в которых располагаются полюсы разомк-
нутой системы. Соответствующая этому изменению
p
функция
∞
<
<
∞
−
Ψ
=Ψ
ω
ω
),()(
||
jp (2.9-41)
легко может быть вычислена.
Участок III – это участок движения комплексной переменной
p
вдоль окружности бесконечно малого радиуса с центром в начале коор-
динат, где по условию находится
1
v полюсов передаточной функции ра-
зомкнутой системы. При этом, в соответствии с (2.9-33), функция
)(
p
Ψ
будет иметь вид
,
)0()(
)0(
lim
)()(
)(
lim)(
1
1
2
211
1
0
1
0
|||
v
jv
v
q
j
v
q
j
jvv
j
e
Qj
S
eQjee
eS
p
ρω
ρωρρ
ρ
ρ
ρ
Θ−
→
ΘΘ
Θ
Θ
→
⋅
−
=
=
−
=Ψ
(2.9-42)
то есть на плоскости
)(
p
Ψ будет иметь место перемещение («доворот»)
по окружности бесконечно большого радиуса. Направление этого пере-
мещения противоположно по знаку направлению перемещения на плос-
кости
p
, а абсолютная величина приращения угла - в
1
v раз больше.
Таким образом, третьему участку соответствует изменение фазы функ-
ции
)(
p
Ψ на величину
π
ϕ
1
|||
v−=Δ
Ψ
. (2.9-43)
Наконец, рассмотрим движение комплексной переменной
p
вдоль ок-
ружности бесконечно малого радиуса с центром в точке
q
jp
ω
= , где
расположено
2
v полюсов передаточной функции разомкнутой системы.
На этом, четвертом участке контура С
0, →+=
Θ
ρ
ρ
ω
j
qIII
ejp . (2.9-44)
В соответствии с (2.9-33), функция
2
2
1
)()(
)(
lim)(
1
0
ν
ρ
ρωω
ω
Θ−
→
⋅=Ψ
jv
q
v
q
q
IV
e
jQj
jS
p
(2.9-45)
будет образовывать годограф, перемещающийся на плоскости
Ψ по ок-
ружности бесконечно большого радиуса, и соответствующее прираще-
ние фазы будет равно
2
2
2
π
ϕ
v
IV
−=Δ
Ψ
. (2.9-46)

100
Пользуясь тем, что
)(
p
Ψ является дробно–рациональной функцией от
p
, и
)()( pp
∗∗
Ψ=
Ψ
, (2.9-47)
можно произвести обход лишь верхней половины контура
C . Тогда
суммарное приращение фазы
).( zm
IVIIIIIISum
−
=
Δ
+
Δ
+Δ+Δ=Δ
ΨΨΨΨΨ
π
ϕ
ϕ
ϕ
ϕ
ϕ
(2.9-48)
Удобнее строить не функцию
)(
p
Ψ
, а функцию )(
p
W . Как видно
из равенства (2.9-34), годограф функции
)(
p
Ψ
поворачивается вокруг
начала координат на тот же угол, что и годограф функции
)(
p
W повора-
чивается относительно точки
)0,1(
j
−
.
Выше приведенные рассуждения позволяют сформулировать кри-
терий устойчивости замкнутой системы, который называют частотным
критерием, или критерием Найквиста.
Критерий Найквиста.
Если передаточная функция разомкнутой системы имеет m по-
люсов с положительной вещественной частью, то для устойчивости
системы в замкнутом состоянии необходимо и достаточно, чтобы
при изменении
ω
от 0 до
∞
+ расширенная амплитудно-фазовая ха-
рактеристика разомкнутой системы повернулась вокруг точки
)0,1(
j
− на угол
π
m+ . Расширение частотной характеристики
)(
ω
j
W необходимо при наличии у передаточной функции разомкнутой
системы полюсов на мнимой оси. Каждому нулевому полюсу соответ-
ствует на амплитудно-фазовой характеристике доворот по окруж-
ности бесконечно большого радиуса на угол
2
π
−
. Каждому чисто
мнимому положительному полюсу соответствует на амплитудно-
фазовой характеристике доворот по окружности бесконечно большо-
го радиуса на угол
π
− .
Естественно, что, давая формулировку критерия устойчивости, ис-
ходят из условия
0=
z
. Можно получить и более общий результат. Ос-
новываясь на формуле (2.9-48), в каждом конкретном случае можно вы-
числить количество «неустойчивых» полюсов замкнутой системы
π
ϕ
SUM
mz
Δ
−= . (2.9-49)
Здесь
SUM
ϕ
Δ – результирующий угол поворота расширенной амплитуд-
но-фазовой характеристики разомкнутой системы вокруг точки
)0,1(
j
−
при изменении
ω
от 0 до ∞+ .
На практике удобнее пользоваться другой формулировкой крите-
рия, которая предложена Я. З. Цыпкиным и использует понятие перехо-
