Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

71
2.8. Графическое представление объектов и систем управ-
ления
Графическое изображение с использованием функциональных
блоков, передаточных функций, сигналов и их изображений называют
структурными схемами. Для представления систем в виде совокупности
отдельных функционально определенных блоков (подсистем) использу-
ются функциональные схемы.
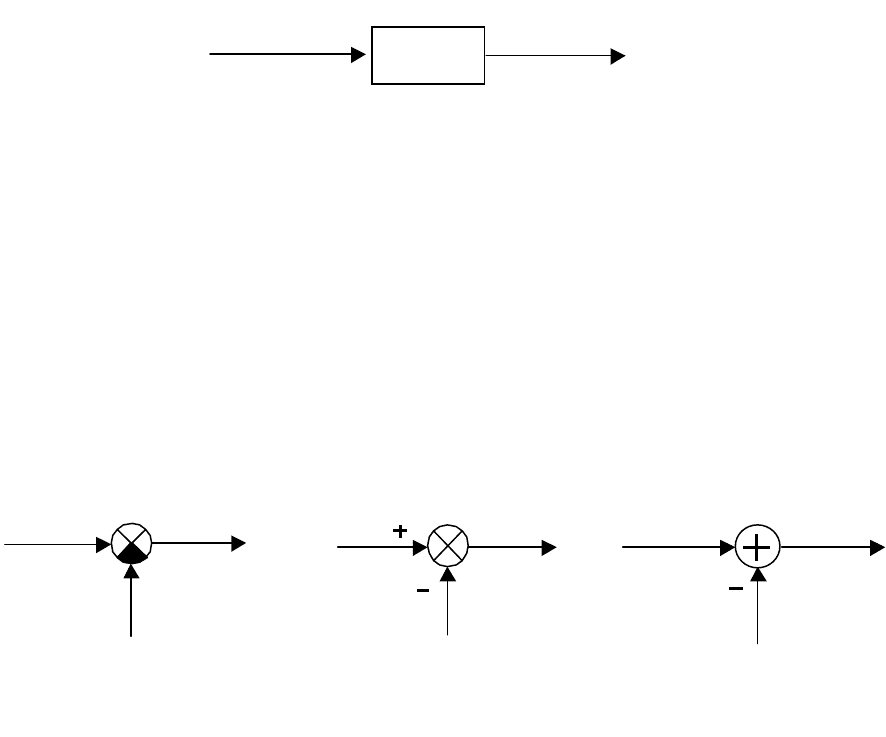
2.8.1. Соглашение об обозначениях
Элементарно-+\.е динамическое звено (система) с передаточной
функцией
)(
p
W представлено на рис 2.20, где
Рис. 2.20. Динамическое звено
)(pY
вх
)(p
Y
вых
)(
p
W
)(pY
вх
– изображение по Лапласу входного сигнала;
)(pY
вых
– изображение по Лапласу выходного сигнала;
)(
p
W – передаточная функция звена;
Связь между элементами выражается уравнением:
)()()( pWpYpY
вхвых
= .
Варианты изображения элементов сравнения, или сумматоров на
структурных схемах представлены на рис.2.21
Рис. 2.21. Элементы сравнения, сумматоры
1
U
2
U
3
U
3
U
1
U
2
U
–
+
3
U
1
U
2
U
Все три варианта равносильны и описываются уравнением:
213
UUU −= .
Если на вход сумматора подается несколько входных сигналов, то
он изображается в виде, представленном на рис.2.22 (три входных сиг-
нала).
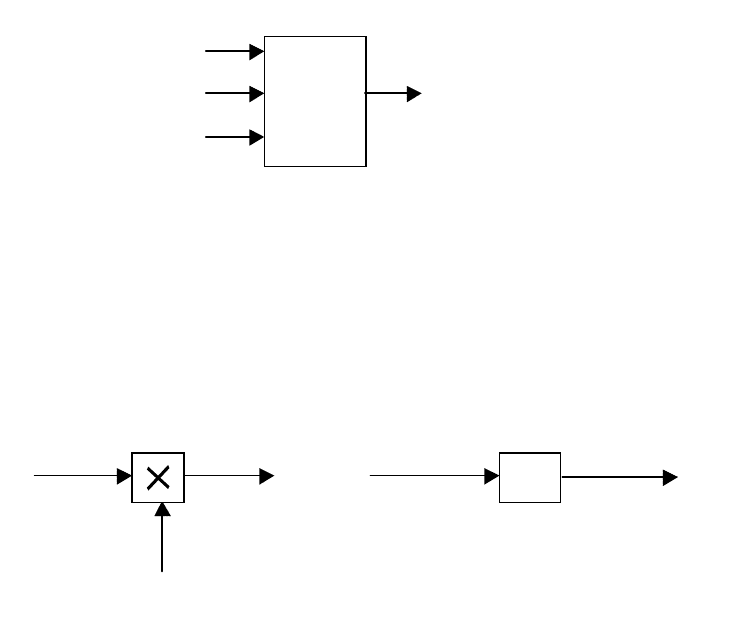
72
4
U
3
U
2
U
1
U
Σ
Рис. 2.22. Сумматор с тремя входными
сигналами
Варианты элементов умножения на структурных схемах пред-
ставлены на рис 2.23. Оба вида равносильны в применении и описыва-
ются уравнением:
12
UKU ×= .
Рис. 2.23. Элементы
у
множения
2
U
1
U
K
1
U
2
U
K
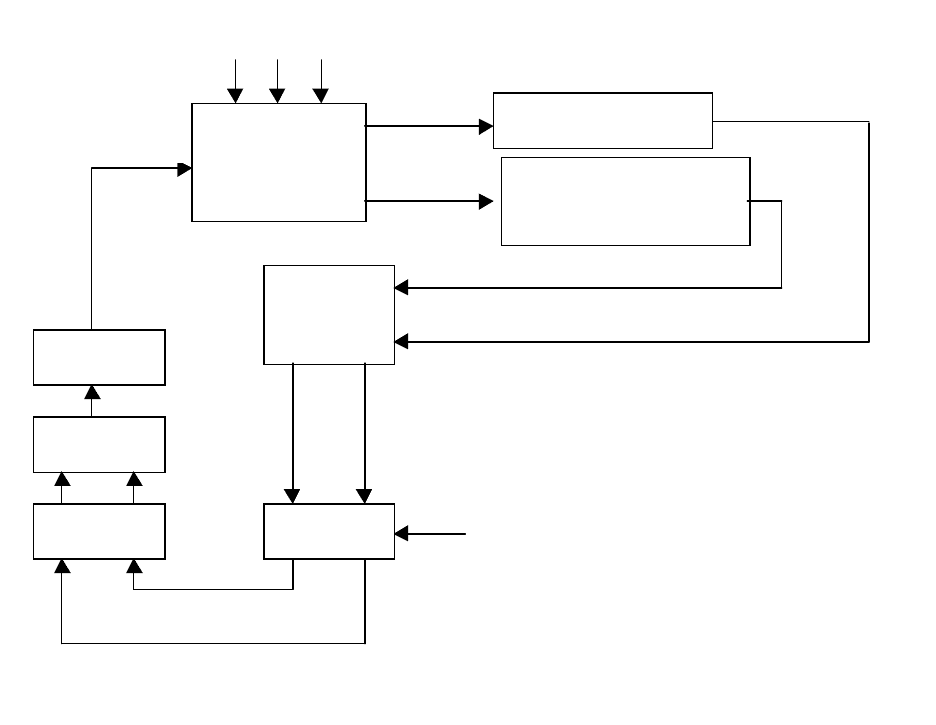
В качестве примера функциональной схемы на рис 2.24 представ-
лена функциональная схема системы стабилизации крена ракеты. На
рисунке использованы обозначения:
БЦВМ – бортовая цифровая вычислительная машина;
УМ – усилитель мощности;
РМ – рулевая машина;
ЦАП – цифро-аналоговый преобразователь;
АЦП – аналого-цифровой преобразователь;
δ
- положение управляющего органа (сопло, руль);
ϕ
- угол крена;
ϕ
&
- угловая скорость крена;
Возмущающие факторы:
W – ветер;
T
– окружающая температура;
AT
P – атмосферное давление;
r
r
– вектор командных сигналов.
73
r
r
W
A
T
P
T
Датчик угловой
скорости
Объект
(ракета)
Датчик угла
РМ
УМ
ЦАП
АЦП
БЦВМ
ϕ
ϕ
&
δ
Рис. 2.24. Функциональная схема угловой стабилизации ракеты
2.8.2. Структурные схемы и графы стационарных систем
2.8.2.1. Типовые соединения многомерных линейных систем
Одной из характерных задач анализа САУ является задача преобразо-
вания и упрощения исходных структурных схем. При этом используются
правила преобразования простейших, типовых соединений, к которым
относят параллельное (согласно-параллельное) - рис 2.25, последова-
тельное – рис 2.26, и встречно-параллельное, когда одно динамическое
звено включено в обратную связь другому –
рис 2.27. Для каждой из этих
ситуаций нетрудно найти передаточную функцию эквивалентного звена.
Пусть исходные динамические звенья имеют следующее описа-
ние:
.)()();()()(
;)()();()()(
22222222
11111111
txCtytuBtxAtx
txCtytuBtxAtx
rrrr
&
r
r
r
rr
&
r
=+=
=+=
(2.8-1)
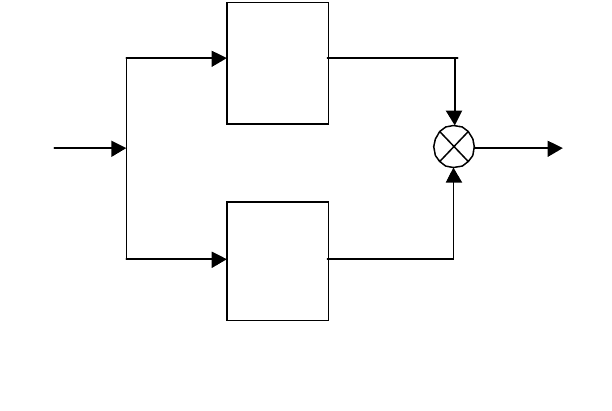
Параллельное соединение (рис. 2.25).
В случае параллельного соединения звеньев введем в рассмотре-
ние следующие очевидные равенства из блочных векторов и матриц
74
[]
⎥
⎦
⎤
⎢
⎣
⎡
⋅=⋅
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
2
1
21
2
1
2
1
2
1
2
1
;
0
0
x
x
CCyu
B
B
x
x
A
A
x
x
r
r
rr
r
r
&
r
&
r
. (2.8-2)
В соответствии с этим можно записать выражение для эквивалентной
передаточной функции соединения
Рис. 2.25. Параллельное соединение
y
r
1
y
r
2
y
r
2
u
r
1
u
r
u
r
1
I
x
r
2
I
I
x
r
BApECpW
1
Э
)()(
−
−
= , (2.8-3)
где:
[]
21
2
1
2
1
;;
0
0
CCC
B
B
B
A
A
A
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
. (2.8-4)
Учитывая, что
21
yyy
r
rr
+= ,
а
)()()();()()(
2211
pUpWpYpUpWpY
r
rrr
== ,
получаем
)()()(
21Э
pWpWpW
+
= . (2.8-5)
С другой стороны, передаточную функцию эквивалентного звена можно
расписать следующим образом:
[]
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
⎥
⎦
⎤
⎢
⎣
⎡
−=⋅−⋅=
−
−
2
1
1
2
1
21
1
0
0
)()(
B
B
A
A
pECCBApECpW
Э
[]
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
−
2
1
1
22
11
21
0
0
B
B
ApE
ApE
CC
n
n
,

75
где:
21
,nn – размерности соответствующих единичных матриц.
Продолжим преобразования:
=
⎥
⎦
⎤
⎢
⎣
⎡
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
−
−
2
1
1
22
1
11
)(0
0)(
)(
B
B
ApE
ApE
CpW
n
n
Э
[]
=
⎥
⎦
⎤
⎢
⎣
⎡
−
−
=
−
−
1
22
1
11
21
)(
)(
ApE
ApE
CC
n
n
2
1
2221
1
111
)()( BApECBApEC
nn
−−
−
+− .
Таким образом, в результате получаем:
,
)(
)(
)(
)(
)(
;)()()(
2
222
1
111
21
pQ
BpIC
pQ
BpIC
pW
pWpWpW
Э
Э
⋅
+
⋅
=
+=
(2.8-6)
где
21
,II
– соответствующие присоединенные матрицы для матриц
1
А и
2
А ;
)(,)(
21
pQpQ - характеристические полиномы первого и второго
звеньев, то есть:
)det()()(
1111
ApEppQ
nA
−
==
ϕ
)det()()(
2222
ApEppQ
nA
−
==
ϕ
Характеристический полином эквивалентной системы (матрицы
А
)
имеет вид:
)()()(
21
pQpQpQ
⋅
= . (2.8-7)
Отсюда следует, что нули характеристического полинома (полюсы) эк-
вивалентной передаточной функции соединения состоят из нулей харак-
теристических полиномов (полюсов передаточных функций) первого и
второго звеньев.
Таким образом, если каждое из параллельных звеньев устойчивы, то и
всё соединение в целом устойчиво; если в соединении присутствует
хотя бы одно неустойчивое звено, то
соединение в целом неустойчи-
во (связь между характером полюсов передаточной функции и устойчи-
востью соответствующей системы будет обсуждаться в п. 2.9).
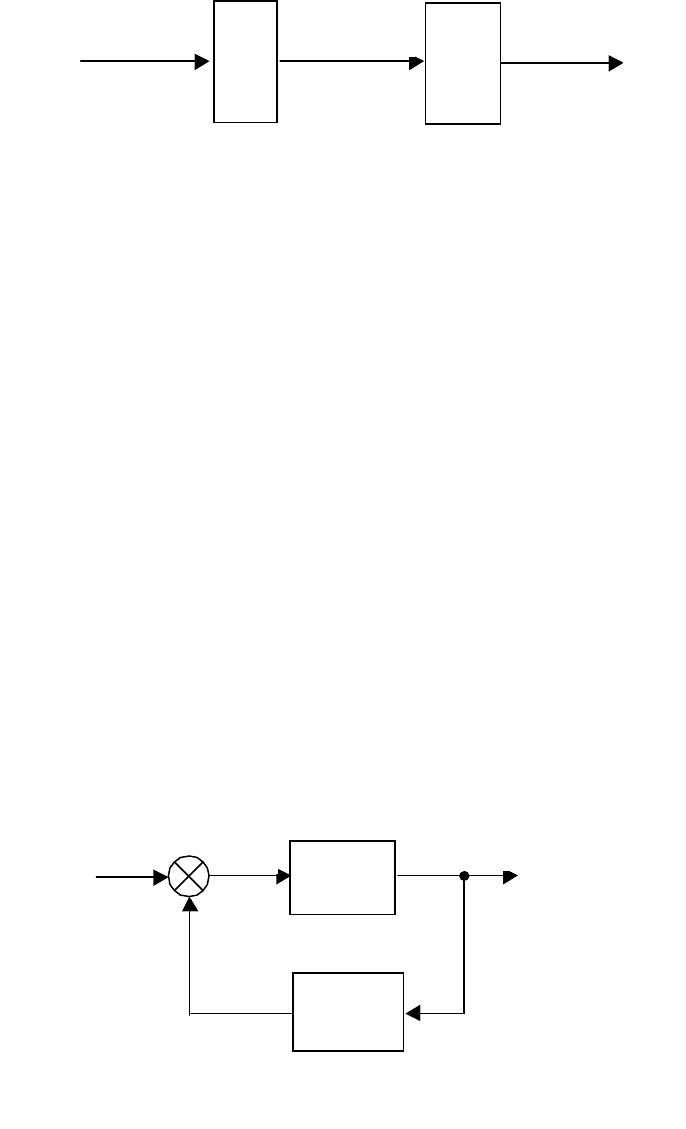
76
Последовательное соединение (рис. 2.26).
При последовательном соединении блочные уравнения имеют вид
yy
r
r
=
2
1
uu
rr
=
1
x
I
r
21
uy
r
r
=
2
II
x
r
Рис. 2.26. Последовательное соединение
[]
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
+
⎥
⎦
⎤
⎢
⎣
⎡
⋅
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
2
1
2
1
2
1
22
1
2
1
0;
0
0
x
x
Cyu
B
x
x
ACB
A
x
x
&
&
, (2.8-8)
и в выражении (2.8-3) для эквивалентной функции
[]
2
1
212
1
0;
0
;
0
CC
B
B
ACB
A
A
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
. (2.8-9)
Кроме того, нетрудно получить связь между передаточными функциями
отдельных звеньев, входящих в соединение, и эквивалентной переда-
точной функцией
)()()(
21Э
pWpWpW = . (2.8-10)
Вывод о связи между устойчивостью отдельных звеньев и устойчиво-
стью их последовательного соединения аналогичен выводу для случая
параллельного включения.
Встречно-параллельное включение звеньев рис. 2.27.
Рис. 2.27. Встречно-паралельное соединение
2
y
r
m
1
x
r
2
x
r
yy
r
r
=
1
u
r
12
yu
r
r
=
1
u
r
Для встречно-параллельного соединения, учитывая, что
21
yuu
r
m
rr
= , получаем:
[]
0;
0
;
1
1
212
211
CC
B
B
ACB
CBA
A
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
m
(2.8-11)
и
77
[]
)()()()(
1
1
21Э
pWpWpWEpW
−
±= . (2.8-12)
Поскольку полюсы передаточной функции эквивалентного соединения в
данном случае не удается выразить непосредственно через полюсы пе-
редаточных функций отдельных звеньев, то однозначного ответа об ус-
тойчивости соединения без дополнительного анализа получить не уда-
ется.
2.8.2.2. Графы динамических систем
Графом называется множество вершин и ребер, в котором каждо-
му ребру соответствует две
вершины - начало и конец ребра.
Основные характеристики графов:
1) каждой вершине на графе, изображаемой кружком или точкой, ста-
вится в соответствие величина одной из переменных (координат сис-
темы);
2) каждое ребро, изображаемое на графе линией со стрелкой, имеет
вершину –“начало” и вершину – “конец”. Стрелка обозначает направ-
ление передачи сигнала от начала
к концу, таким образом, граф про-
хождения сигналов является направленным (антисимметричным)
графом;
3) величина, соответствующая началу (вершине) ребра, называется
входной величиной ребра. Если из вершины выходит несколько ре-
бер, то входные величины этих ребер одинаковы и равны величине
соответствующей вершины;
4) ребро изображает одно из звеньев в системе и ему ставится
в соот-
ветствие передаточная функция;
5) если к вершине подходит несколько ребер, то сопоставляемая ей
величина равна сумме выходных величин ребер.
Между графом прохождения сигналов и структурной схемой имеется
взаимно - однозначное соответствие. Стрелка структурной схемы соот-
ветствует вершине графа, а прямоугольник (звено) – ребру. При необхо-
димости в граф системы могут вводиться
дополнительные единичные
ребра для выявления промежуточных координат, являющихся, в основ-
ном, выходами отдельных ребер. Для примера, приведены графические
представления некоторой системы в виде структурной схемы (рис 2.28)
и графа (рис 2.29).
Простейшие правила преобразования структурных схем и графов
линейных систем представлены в таблице 2.1.
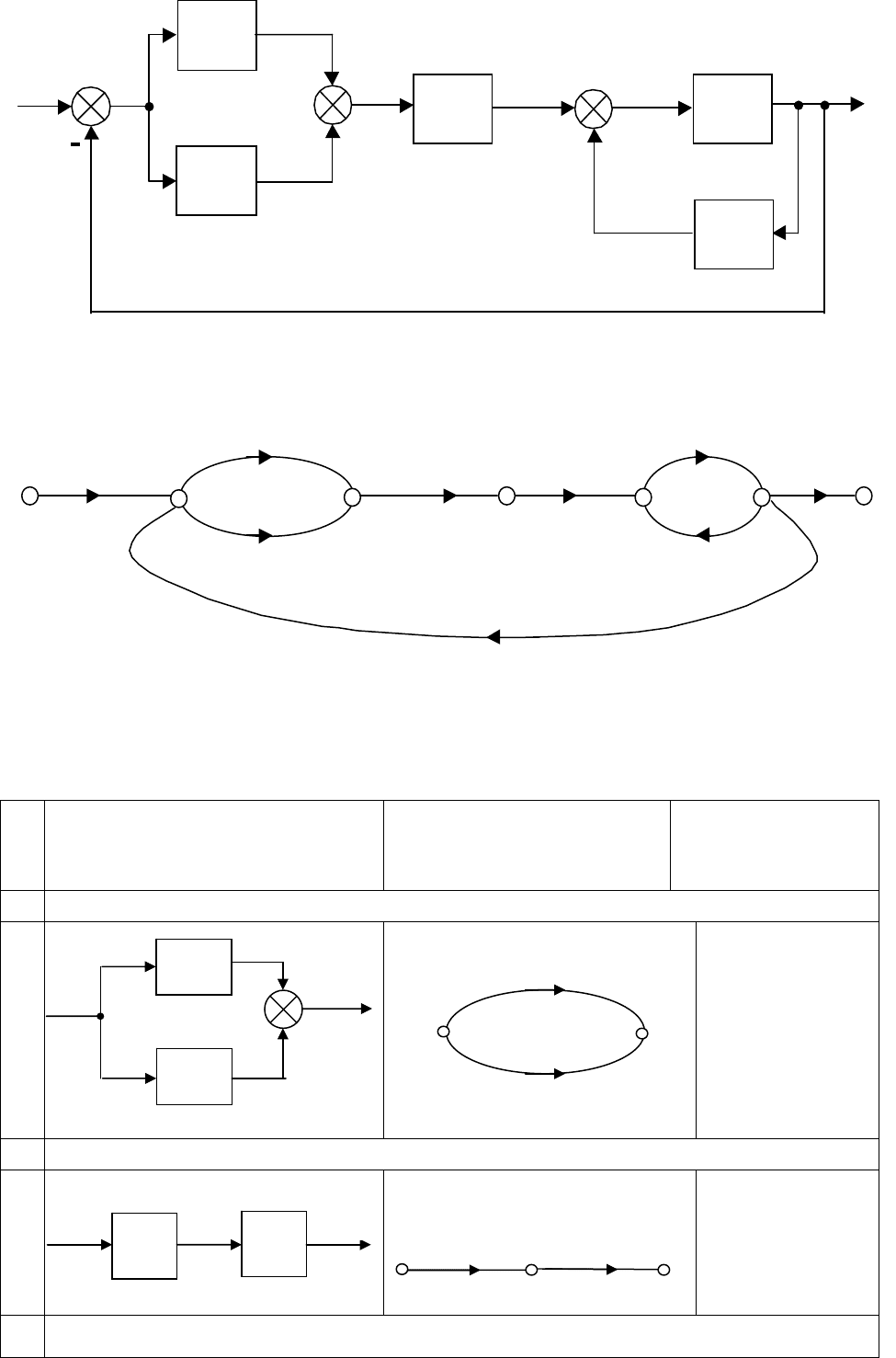
78
Рис. 2.28. Структурная схема системы
y
4
u
5
y
y
3
1
y
3
u
ε
v
2
y
W
5
W
4
W
3
W
1
W
2
Рис. 2.29. Граф системы
-1
y
v
W
5
4
u
ε
y
1
W
1
1
W
2
3
u
W
3
y
3
1
W
4
y
1
Таблица 2.1
№ Структурная схема Граф Эквивалентная
передаточная
функция
1 Параллельное соединение звеньев.
)(
)(
2
1
pW
pWW
Э
+
+
=
2 Последовательное соединение звеньев.
)(
)(
2
1
pW
pWW
Э
⋅
⋅
=
3 Встречно-параллельное соединение звеньев.
1
W
2
W
U
y
U
1
W
2
W
y
U
1
W
y
2
W
U
y
1
W
2
W
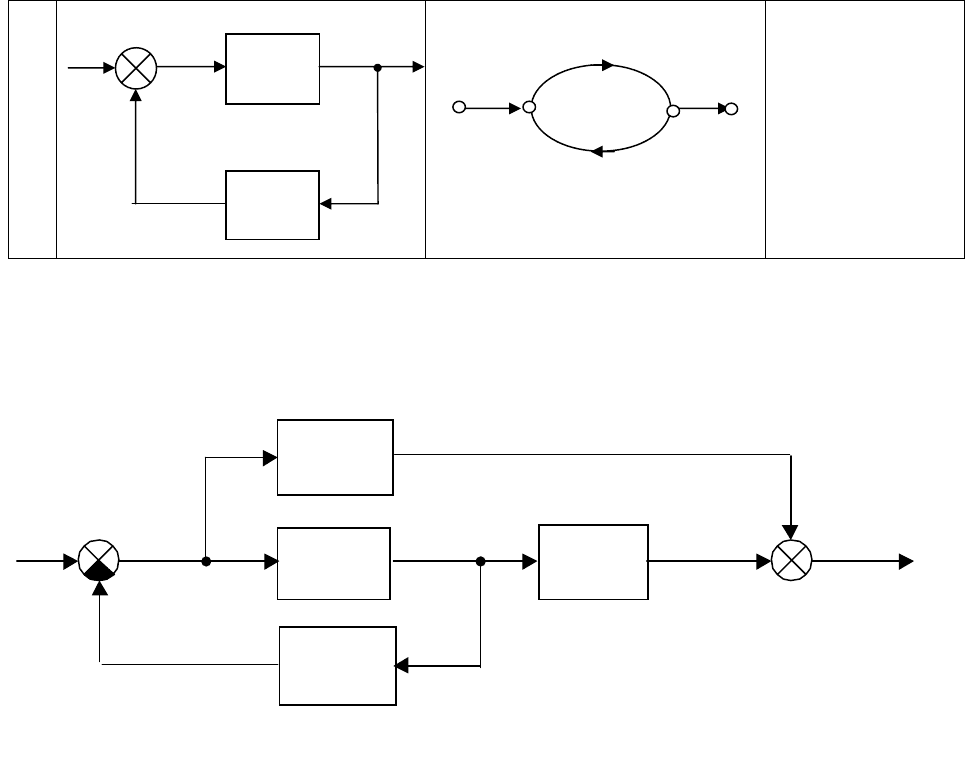
79
)()(1/
/)()(
21
1
pWpW
pWpW
э
±
=
Встречаются и более сложные случаи соединения звеньев, так,
например, соединения с перекрестными связями (рис. 2.30).
Рис. 2.30. Соединение с перекрестными связями
y
p
1
p
2
W
1
W
2
W
3
W
4
u
S
1
S
2
В этих случаях можно пользоваться правилом переноса динамического
звена через сумматор или точку разветвления.
Любое динамическое звено можно перенести через сумматор
или точку разветвления; при этом звено должно войти во все входя-
щие и ответвляющиеся ветви. В те ветви, в которые звено входит
без изменения направления распространения сигнала, звено
проходит
со своей передаточной функцией. В тех ветвях, при продвижении в
которые меняется направление распространения сигнала, переда-
точная функция звена изменяется на обратную.
Это правило иллюстрируется элементарными примерами, приве-
дёнными на рис. 2.31÷2.34.
m
U
1
W
2
W
y
1
W
U
2
W
m
1
1
80
Рис. 2.31. Перенос звена
W
через точку разветвления
p
y
y
y
y
u
p
u
W W
W
Рис. 2.32. Перенос звена
W
через сумматор
S
1
u
S
S
1
u
2
u
W W
y
y
2
u
W
p
y
2
W
3
p
W
1
W
2
u
y
1
W
2
y
1
W
1
W
3
1/
W
2
u
y
2
Рис. 2.33. Перенос звена
W
2
через точку разветвления
p
