Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

41
В вырожденном случае
0
=
n
α
. Иллюстрацией этого может служить
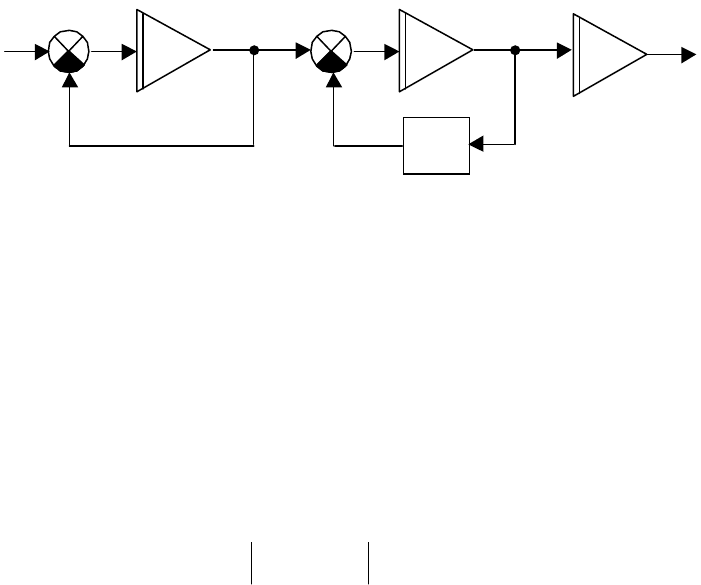
объект, структурная схема которого приведена на рис.2.9.
u x
2
x
3
x
1
2
Рис.2.9. Структурная схема. Вариант с
0
=
n
α
2.4.2. Собственные значения и собственные векторы транспониро-
ванной матрицы
Собственные значения транспонированной матрицы, это такие
λ
, для
которых система уравнений
dd
A
T
r
r
λ
= (2.4-7)
имеет нетривиальные решения, т.е. когда
0=−
T
AE
λ
. (2.4-8)
Решение этого алгебраического уравнения дает
n значений собст-
венных чисел
n
λ
λ
λ
,...,,
21
. Так как определитель квадратной матрицы
и её транспонированной матрицы равны, то собственные числа матриц
A
и
T
A
также равны.
Таким образом, собственному числу
i
λ
соответствует собственный век-
тор
i
v
r
матрицы
A
и собственный вектор
i
d
r
матрицы
T
A
.
Если транспонировать обе части уравнения (2.4-7), то получим:
TT
d
A
d
r
r
λ
= . (2.4-9)
В связи с этим вектор
d
r
называют левым собственным вектором матри-
цы
A
, в отличие от v
r
, который, в таком случае, называют правым соб-
ственным вектором. Для
i
-го собственного числа и
i
-го левого собст-
венного вектора соответственно
T
ii
T
i
dAd
r
r
λ
= .
Умножим обе части этого равенства справа на вектор
j
v
r
:
j
T
iij
T
i
vdvAd
r
r
r
r
λ
= . (2.4-10)
Учитывая свойства собственных векторов, в результате получаем урав-
нение
42
j
T
iijj
T
i
vdvd
r
r
r
r
λλ
= ,
которое преобразуется к виду
0)( =−
ijj
T
i
vd
λλ
r
r
. (2.4-11)
Полагаем, что все собственные числа матрицы
A
различны. Тогда для
j
i ≠ имеем
ji
λ
λ
≠ и из равенства (2.4-11) следует, что векторы
T
i
d
r
и
j
v
r
взаимно ортогональны:
jivd
j
T
i
≠= ,0
r
r
. (2.4-12)
Это означает то, что
i
d
r
ортогонален )1(
−
n - мерной гиперплоскости, с
базисом, образованным векторами
j
v
r
для всех i
j
≠
.
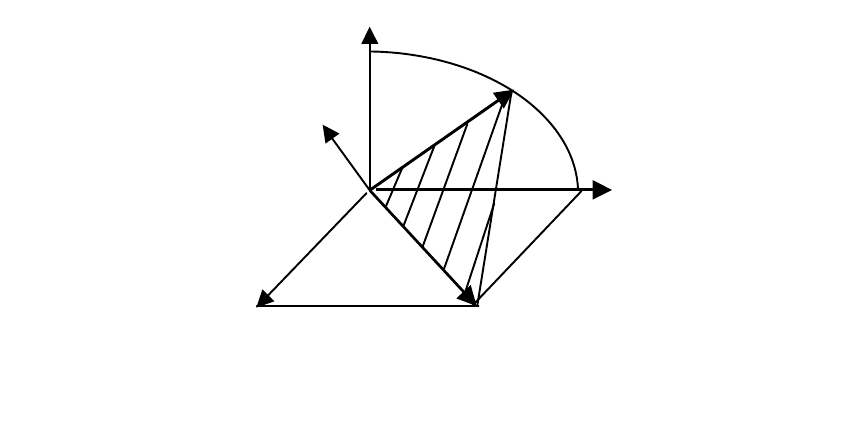
В качестве примера на рисунке 2.10
показан один из вариантов взаим-
ного расположения правых и левых собственных векторов некоторой
матрицы
A
для случая 3=n . Здесь хорошо видно, что каждый из век-
торов
i
d
r
ортогонален всем векторам
i
v
r
при i
j
≠
.
3
v
r
2
v
r
1
v
r
3
d
r
1
d
r
2
d
r
Рис. 2.10. Пример взаимного расположения правых и
левых собственных векторов
Теперь рассмотрим случай, когда
j
i
=
. При этом скалярные произведе-
ния векторов
i
d
r
и
i
v
r
не должны быть равны нулю. Если предположить,
что 0=
i
T
i
vd
r
r
, то придется утверждать, что вектор
i
d
r
ортогонален всему
n – мерному пространству с базисом
n
vvv
r
K
r
r
,,,
21
. Но этого не может
быть, так как вектор
i
d
r
сам принадлежит этому пространству. Таким об-
разом,
niдляvd
i
T
i
,...,2,10 =≠
r
r
. (2.4-13)

43
В связи с тем, что собственные векторы можно выбирать с точностью до
постоянного (в том числе комплексного) сомножителя, то наборы, иначе
говоря, базисы
{}
v
r
и
{
}
d
r
формируют так, чтобы для ni ,...,2,1= вы-
полнялось условие
niдляvd
i
T
i
,...,2,11 ==
r
r
. (2.4-14)
Отметим ещё одно важное свойство собственных векторов:
Если матрица
A
не имеет кратных собственных чисел, то все её
собственные векторы линейно независимы, то есть образуют базис
в пространстве
n
R
. Это нетрудно доказать.
Действительно, предположим сначала, что среди собственных векторов
матрицы
A
первые два являются линейно зависимыми, то есть
∑
=
=
2
1
0
i
ii
v
r
γ
, (2.4-15)
где ни один из коэффициентов
1
γ
и
2
γ
не равен нулю. Умножив это
уравнение слева на
A
, получим
0
2
1
=
∑
=i
iii
v
r
λγ
. (2.4-16)
Теперь умножим (2.4-15) на
2
λ
:
∑
=
=
2
1
2
0
i
ii
v
r
λγ
. (2.4-17)
Вычтем (2.4-17) из (2.4-16) и в результате получим
0)(
1211
=
− v
r
λ
λ
γ
.
Из того, что
21
λ
λ
≠ и 0
1
≠
γ
следует 0
1
=
v
r
, чего не может быть, следо-
вательно, первые два собственных вектора не могут быть линейно зави-
симыми.
Теперь предположим, что число линейно зависимых векторов рав-
но
2>r , то есть
riv
i
r
i
ii
,...,2,1:0,0
1
=≠=
∑
=
γγ
r
.
Умножив это уравнение слева на
A
, получим
0
1
=
∑
=
r
i
iii
v
r
λγ
. (2.4-18)
Умножим (2.4-18) на
r
λ
:
0
1
=
∑
=
r
i
iri
v
r
λγ
. (2.4-19)
44
Вычтем (2.4-19) из (2.4-18) и в результате будем иметь
∑
−
=
=−
1
1
0)(
r
i
irii
v
r
λλγ
.
Получается, что число линейно зависимых векторов
rr <− 1 . Если со-
гласиться с этим, то дойдём до
2
=
r , и круг замкнулся.
Таким образом, действительно, все собственные векторы матрицы
A
являются линейно независимыми, поэтому матрица
[
]
n
vvv
V
rrr
,...,,
21
= , построенная из векторов базиса
{
}
v
r
, т.е. из правых
собственных векторов матрицы
A
, является невырожденной. Эта мат-
рица называется модальной матрицей. Из перечисленных выше свойств
для правых и левых собственных векторов следует равенство:
E
V
D
T
=
, или
1−
=
V
D
T
. (2.4-20)
T
D - матрица, строки которой, являются транспонированными векторами
двойственного базиса
{
}
d
r
, т.е. левыми собственными векторами матри-
цы
A
:
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅⋅
=
T
n
T
T
T
d
d
d
D
r
r
r
2
1
. (2.4-21)
2.4.3. Определение функции от матрицы через её левые и правые
собственные векторы
Все n систем уравнений
nivvA
iii
,...,2,1, ==
rr
λ
могут быть записаны с использованием блочных матриц:
]...[]...[
221121 nnn
vvvvAvAvA
r
r
r
rrr
λλλ
= .
Учтем, что
AVvAvAvA
n
=]...[
21
r
rr
,
и
[]
=
nn
vvv
r
L
rr
λ
λ
λ
2211

45
,
00
00
00
2
1
21
22221
11211
Λ=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
= V
vvv
vvv
vvv
nnnnn
n
n
λ
λ
λ
L
LLLL
L
L
L
LLLL
L
L
где
Λ- диагональная матрица собственных чисел.
Таким образом, получено равенство
Λ=
V
AV
,
или
T
D
V
A
Λ= . (2.4-22)
Преобразование
1−
= TC
T
A
, где
T
- произвольная невырожденная
матрица, называется преобразованием подобия. Одно из основных
свойств этого преобразования заключается в том, что собственные чис-
ла подобных матриц (здесь -
A
и C ) совпадают. Действительно,
)()(
111
λ
ϕ
λ
λ
λ
λ
ϕ
CA
TCETTCTTTAE
=
−
=
−
=−=
−−−
.
Говорят, что матрица
A
приводится к диагональному виду преобразо-
ванием
AV
D
AV
V
T
==Λ
−1
. (2.4-23)
Более высокие степени
A
приводятся к диагональному виду таким же
способом:
V
A
V
AV
A
V
V
V
21112 −−−
=
=Λ
.....................................................
V
A
V
ll 1−
=Λ или
1−
Λ
=
V
V
A
ll
.
Таким образом, если рассмотреть матричный многочлен
,)(
1
1
1
ECACACAAN
ll
ll
+
+
++=
−
−
K
то
{
}
,)(
1
1
1
1
−
−
−
+
Λ
+
+Λ
+
Λ= VECCCVAN
ll
ll
K
или
.
1
2
1
)(00
0)(0
00)(
)(
−
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅⋅⋅
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
⋅⋅⋅
⋅
⋅
⋅
= V
N
N
N
VAN
l
λ
λ
λ
. (2.4-24)

46
Если применить этот результат к характеристическому полиному, то по-
лучим
,0)( =
A
ϕ
(2.4-25)
то есть каждая квадратная матрица удовлетворяет своему характе-
ристическому полиному. Это утверждение известно в теории матриц как
теорема Кэли-Гамильтона.
Для любой функции от матрицы
)(
A
f , которую можно представить в ви-
де конечного или бесконечного степенного полинома, справедливо ана-
логичное выражение
T
n
D
f
f
f
VAf ⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
⋅=
)(00
0)(0
00)(
)(
2
1
λ
λ
λ
K
MMM
K
K
, (2.4-26)
или эквивалентное ему
.)()(
1
∑
=
=
n
i
T
iii
dvfAf
r
r
λ
(2.4-27)
Отсюда вытекает, например, один из способов определения матричной
экспоненты или соответствующей переходной матрицы:
∑
=
==Φ
n
i
T
ii
t
i
At
dveet
1
.)(
r
r
λ
(2.4-28)
ПРИМЕР 2.4-2.
Для объекта, представленного на рис.2.8. в примере 2.4-
1, найдём левые собственные векторы. Если обозначить присоединён-
ную матрицу к матрице
A
как }{
A
I
, то очевидно равенство
}{}{ AIAI
TT
= .
Поэтому
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+++
+++
+
+
==
6531
0341
0023
}{)(
2
2
2
λλλ
λλλ
λ
λ
λ
Td
AII .
Учитывая, что
3;2;1
321
−
=
−=−=
λ
λ
λ
,
имеем:

47
;
011
011
000
)(;
221
000
000
)(
21
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
λλ
dd
II
;
001
002
002
)(
3
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
λ
d
I
Рассчитаем левые собственные векторы. Учтем при этом (2.4-14). Таким
образом, для первого собственного вектора
1
d
r
должны выполняться ус-
ловия
[]
12,100
11111
===
νν
vdd
TT
r
r
r
,
откуда
2
1
1
=
ν
и
[]
5.000
1
=
T
d
r
.
Аналогично получим
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
5.0
1
1
;
1
1
0
32
dd
rr
.
Теперь можно записать выражение для переходной матрицы. Из (2.4-28)
имеем
tttAt
eeee
32
000
000
5.011
000
110
110
100
100
5.000
−−−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
+
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
и окончательно
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+−−
=
−
−−−
−−−−−−
t
ttt
tttttt
At
e
eee
eeeeee
e
00
0
5.05.0
22
32323
.
Рассмотрим ещё несколько примеров.
Для
48
;3;2;1;
100
120
013
321
−=−=−=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
λλλ
A
имеем
.
100
2120
2
3
2
2
1
323
000
000
5.011
3
000
110
110
2
100
100
2
1
00
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
+−−
=
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
+
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
+
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
j
jjjA
Проведём проверку:
.
100
120
013
100
2120
2
3
2
2
1
323
100
2120
2
3
2
2
1
323
2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
+−−
⋅
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
+−−
j
Для той же матрицы найдём
5
A
:
243,32,1
5
3
5
2
5
1
−
=
−
=
−=
λ
λ
λ
и

49
.
100
31320
90211243
000
000
2
1
11
243
000
110
110
32
100
100
2
1
00
5
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−−
=
=
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−=A
2.5. Свойства движений линейных систем
2.5.1. Матричная весовая и переходная функции
Пусть заданы уравнения некоторого динамического объекта
)()()()( tutBxtAtx
r
r
&
r
+= ; (2.5-1)
)()()( txtCty
r
r
= . (2.5-2)
В соответствии с формулой Коши выражение для вектора выхода
ξξξξ
duBttCtxtttCty
t
t
)()(),()()(),()()(
0
0
rrr
∫
Φ+Φ= . (2.5-3)
Анализируя качество работы объекта, удобно рассматривать движение
)(ty
r
как сумму свободной составляющей, обусловленной, в основном,
свойствами самого объекта, и вынужденной составляющей, несущей от-
печаток входного сигнала - вектора управления. Строго говоря, это раз-
деление условно, но очевидно, что свободную составляющую целесо-
образно отождествить с первым слагаемым правой части равенства
(2.5-3). Отсюда следует вывод, что основные свойства объекта опреде-
ляются его
переходной матрицей
(
)
0
,tt
Φ
, в то время как степень их
проявления зависит от вектора начальных условий.
Отметим, однако, что первопричиной всякого движения объекта являет-
ся вектор управления. Это означает, что даже при анализе собственных
движений объекта следует учитывать и матрицу управления
)(tB .
Обозначим
() ()
(
)
(
)
τ
τ
τ
BttCtw
y
,, Φ= . (2.5-4)
Очевидно, что для
i -й координаты вектора выхода при нулевых началь-
ных условиях справедливо выражение
50
() ( ) ( )
∫
∑
=
=
t
t
n
j
jiji
u
dutwty
0
1
,
ξξξ
.
Если положить
)()(
τ
ξ
δ
ξ
−
=
k
u
и
0)( =
ξ
j
u при k
j
≠
, то в соответствии со свойствами
δ
-функции по-
лучим
),()(
τ
twty
iki
= .
Таким образом, элемент, стоящий в
i -ой строке и в k -м столбце
матрицы
()
τ
,tw
y
, можно интерпретировать как реакцию i -ой коорди-
наты вектора
(
)
ty
r
на дельта-функцию
(
)
τ
δ
−
t в k -ой координате
вектора управления
()
tu
r
.
Матрица
()
τ
,tw
y
называется матричной весовой или матричной им-
пульсной переходной функцией объекта по вектору выхода. Аналогич-
ным образом определяется матричная весовая функция объекта по век-
тору состояния
(
)()
(
)
τ
τ
τ
Bttw
x
,, Φ= . (2.5-5)
2
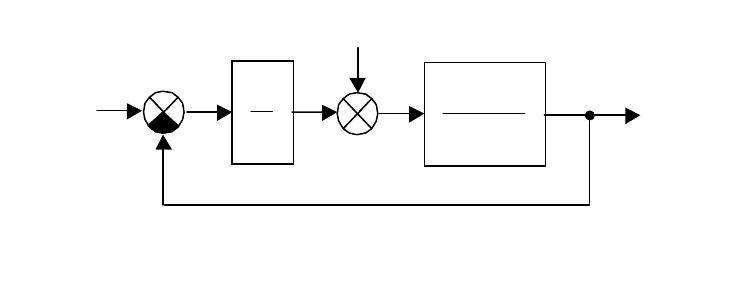
u
1
u
2
x
1
x
p
k
12
10
+p
Рис. 2.11. К примеру на определение матричной
весовой
фу
нкции
Интеграл от матричной весовой функции
() ()
ττ
dtwttH
t
t
∫
=
0
,,
0
(2.5-6)
называют матричной переходной функцией объекта. Элементы этой
матрицы могут рассматриваться как реакции координат вектора выхода
(вектора состояния) на единичные функции по соответствующим коор-
динатам вектора управления. Если на вход объекта поступает постоян-
ный во времени вектор управления
)(1
00
ttu
−
×
r
, то при нулевых на-
чальных условиях
(
)()
00
, uttHty
r
r
= . (2.5-7)
