Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.


21
Множество всех значений, которые может принять вектор
u
r
в мо-
мент времени
t , образует пространство управления. Аналогично вво-
дятся понятия пространства возмущений, пространства выходов и про-
странства состояний.
В любой момент времени
t состояние системы является функцией
начального состояния
)(
0
tx
r
и векторов
),(
0
ttu
r
и ),(
0
ttf
r
. Если известно,
как изменялись эти векторы на интервале
],[
0
tt , то однозначно может
быть определено состояние системы
)(tx
r
:
)},(),,(),({)(
000
ttfttutxFtx
r
rrr
= . (2.1-1)
Вектор выхода в момент времени
t является функцией тех же пе-
ременных:
)},(),,(),({)(
000
ttfttutxty
r
rr
Ψ= . (2.1-2)
Состояние системы отделяет будущее от прошлого, так что состо-
яние содержит всю информацию, необходимую для определения реак-
ции объекта на произвольный входной сигнал. Понятие состояния явля-
ется основным исходным понятием и, следовательно, не может быть
определено более полно, чем, например, слово "множество" в матема-
тике. Наибольшее, что можно сделать, это
сформулировать свойства,
какими должна обладать система, поведение которой отвечает понятию
состояния.
Основным свойством состояния является то, что будущие значе-
ния его не зависят от характера достижения системой её текущего со-
стояния. Состояние системы в данный момент времени, а также текущее
и будущие значения её входов единственным образом определяют на-
стоящее и
будущие значения её состояния и выходов.
Уравнение (2.1-1) называют уравнением состояния системы, а
уравнение (2.1-2) - уравнением выхода. Если объект описывается диф-
ференциальным уравнением, то уравнения (2.1-1) и (2.1-2) превращает-
ся в
}),(),(),({)( ttftutxFtx
r
rr
&
r
= ,
00
)( xtx
r
r
=
; (2.1-3)
)}(,),(),(),({)( tvttftutxty
r
r
rr
Ψ= , (2.1-4)
где дополнительно введён вектор ошибок измерений
)(tv
r
.
Как правило, выбор состояния естественным образом следует из
физического устройства системы, а уравнение (2.1-3), называемое
дифференциальным уравнением состояния, обычно следует из элемен-
тарных физических законов, которыми определяется её поведение.

22
2.2. Линеаризация исходных уравнений
Почти все реальные объекты и системы автоматического управле-
ния являются нелинейными. Однако, среди нелинейных функций
F
и
Ψ
часто встречаются такие, которые при определённых допущениях в ра-
бочей области функционирования системы могут быть заменены линей-
ными. В качестве примера такого случая представлена элементарная
функция на рис.2.2. В данном случае возможна линеаризация, так как
если точка
A
перемещается на небольшие расстояния по кривой
)(
12
VfV = , то этот участок кривой можно заменить отрезком прямой. В
то же время, нелинейная функция на рис.2.3 не допускает подобную за-
мену, если в процессе работы системы происходит изменение уровня
выходного сигнала
2
V . Системы с такого типа функциями называют су-
щественно нелинейными. Их исследованию будет посвящен специаль-
ный раздел пособия. Ниже будет рассмотрен класс систем, допускаю-
щих линеаризацию.
A
V
2
V
2
V
1
V
1
Рис. 2.2. Линеаризуемая
нелинейность
Рис. 2.3. Существенная
нелинейность
Пусть режим функционирования объекта определяется некоторой
траекторией по вектору управления
)(
0
tu
r
, а действительная реализация
)(tu
r
близка к ней:
)()()(
0
tututu
r
rr
Δ
+= . (2.2-1)
При этом решение уравнения (2.1-3) можно записать в виде
)()()(
0
txtxtx
r
rr
Δ
+= , (2.2-2)
где
)(
0
tx
r
– решение уравнения (2.1-3) при )(
0
tuu
=
r
.
Назовём функционирование объекта (системы) при
)(
0
tuu =
r
базо-
вым режимом. Переменные
)(),(),( tftutx
r
r
r
ΔΔΔ – это отклонения от со-
ответствующих переменных в базовом режиме.
Подставим теперь выражения для
)(tx
r
и
)(tu
r
в исходное диффе-
ренциальное уравнение состояний

23
}),()(),()(),()({)()(
0000
ttftftututxtxFtxtx
r
r
r
r
r
r
&
r
&
r
Δ+Δ+Δ+=Δ+
и разложим функцию
F
в ряд Тейлора:
.},,,{},,,{
},,,{},,,{)()(
000000
0000000
RftfuxJutfuxJ
xtfuxJtfuxFtxtx
fU
x
+Δ+Δ+
+Δ+=Δ+
rr
rrr
r
rr
r
r
r
r
r
rr
&
r
&
r
(2.2-3)
Здесь
R
– остаточный член, содержащий высшие степени приращений,
и им можно пренебречь,
fux
JJJ ,, – матрицы Якоби функции
F
для
x
r
,
u
r
и
f
r
.
Элемент матрицы Якоби определяется как соответствующая част-
ная производная
k
i
ikx
dx
dF
J =)(
. Например, для системы второго порядка
соответствующее слагаемое в правой части (2.2-3) имеет вид
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
Δ
∂
∂
+Δ
∂
∂
Δ
∂
∂
+Δ
∂
∂
=
⎥
⎦
⎤
⎢
⎣
⎡
Δ
Δ
⋅
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
∂
∂
∂
∂
∂
∂
∂
∂
=Δ⋅
2
2
2
1
1
2
2
2
1
1
1
1
2
1
2
2
1
2
2
1
1
1
x
x
F
x
x
F
x
x
F
x
x
F
x
x
x
F
x
F
x
F
x
F
xJ
x
r
,
Пренебрегая в (2.2-3) остаточным членом
R
и учитывая уравнение
для базового режима, получим:
ftfuxJutfuxJxtfuxJtx
fUx
rr
r
r
r
r
r
r
r
r
rr
&
r
Δ+Δ+Δ=Δ },,,{},,,{},,,{)(
000000000
. (2.2-4)
Введем обозначения:
{
}
{}
{}
.)(),(),(),()(
;),(),(),()(
;),(),(),()(
000
000
000
tfttftutxJtG
ttftutxJtB
ttftutxJtA
f
u
x
rr
rr
r
rr
r
r
r
Δ=
=
=
В результате получим:
Линейное дифференциальное векторно-матричное уравнение с пере-
менными параметрами (коэффициентами)
)()()()()()()( tftGtutBtxtAtx
r
r
r
&
r
Δ⋅+Δ⋅+Δ⋅=Δ , (2.2-5)
Аналогичным образом проведем линеаризацию уравнения выхода:
24
)()()()()()( tvtutDtxtCty
r
r
rr
Δ
+
Δ
⋅
+Δ
⋅
=Δ . (2.2-6)
Впредь, рассматривая линейные модели системы, будем опускать сим-
вол Δ при записи приращений соответствующих векторов. Таким обра-
зом, линеаризованные уравнения объекта (системы) примут вид
)()()()()()()( tftGtutBtxtAtx
r
r
r
&
r
++= ; (2.2-7)
)()()()()()( tvtutDtxtCty
r
r
rr
+
+= . (2.2-8)
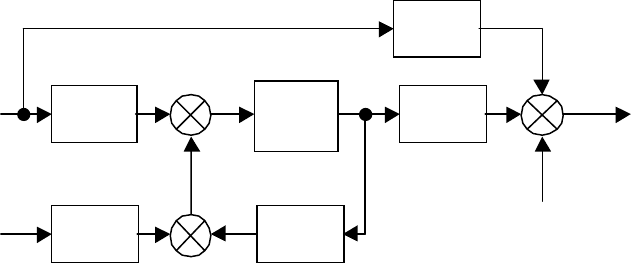
Ha рис. 2.4 приведена структурная схема, являющаяся графичес-
ким изображением уравнений (2.2-7) и (2.2-8).
Рис. 2.4. Обобщённая структурная схема объекта
управления
)(
t
B )(
t
C
)(
t
D
)(
t
G )(
t
A
)(tx
r
)(tf
r
)(tu
r
)(t
v
r
)(ty
r
∫
В качестве примера рассмотрим смесительный бак, который на-
полняется с помощью двух потоков, имеющих переменные мгновенные
расходы
)(
1
tF и )(
2
tF (рис. 2.5). Оба входных потока содержат раство-
римое вещество с неизменными концентрациями
1
C и
2
C . Выходной по-
ток имеет массовую скорость истечения (мгновенный расход)
)(t
F
.
Предполагается, что содержимое бака перемешивается так, что концен-
трация выходного потока равна концентрации
)(tC
out
в баке.
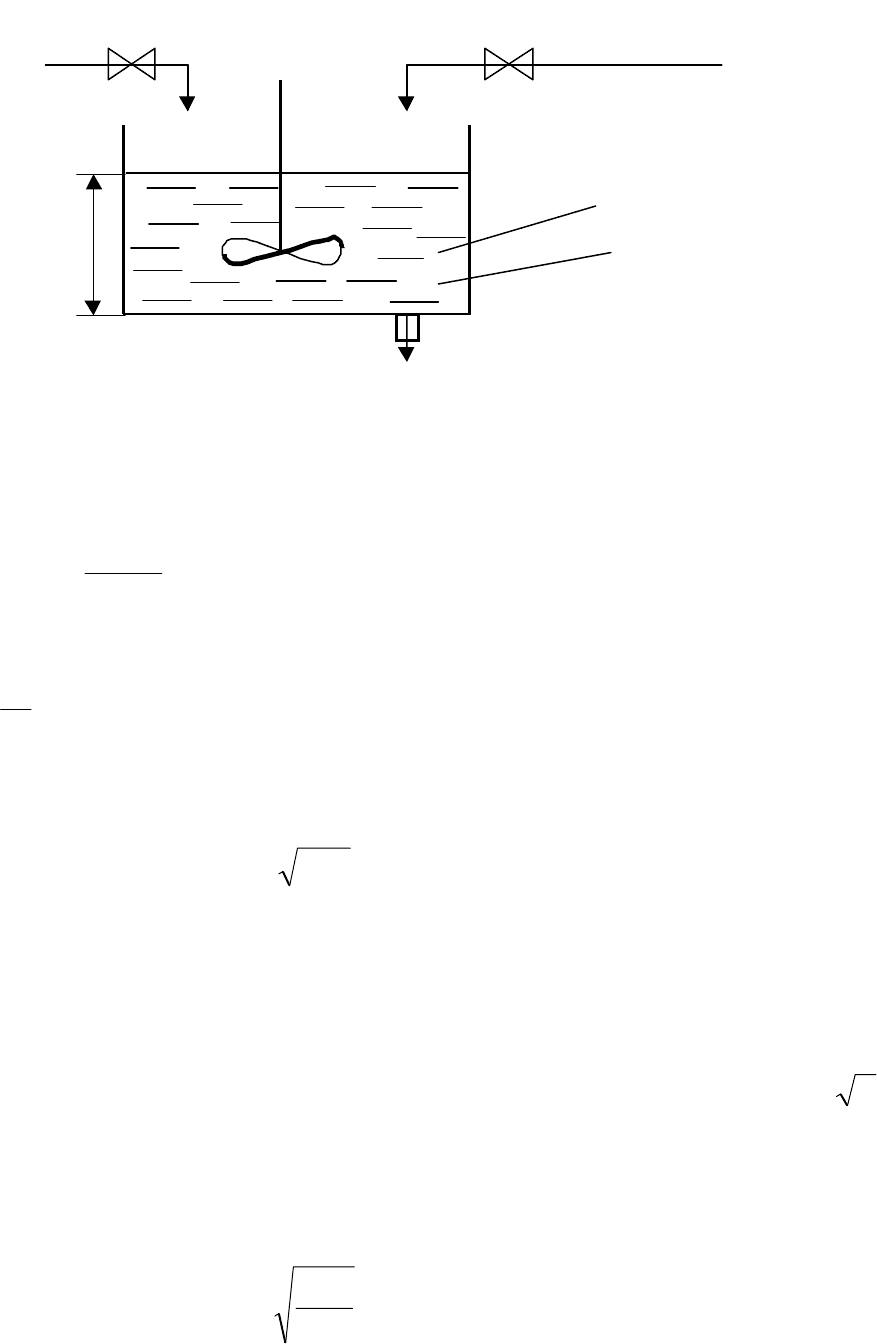
25
C
ou
t
(t)
h(t)
F(t),C
out
(t)
F
1
(t)
C
1
C
2
-
концентрация
Рис. 2.5. Смесительный бак
V(t)
– объем
F
2
(t)
-
расход
выход
Запишем уравнения баланса масс в баке.
Для полной массы:
).()()(
)(
21
tFtFtF
d
t
tdV
−+=
(2.2-9)
Для массы растворённого вещества:
).()()()()}()({
2211
tFtCtFCtFCtVtC
d
t
d
outout
−+= (2.2-10)
Мгновенный расход выходного потока при естественном истечении за-
висит от уровня жидкости в баке
)(th следующим образом:
)()( thktF = , (2.2-11)
где
k - некоторая константа. Это следует из уравнения Бернулли, кото-
рое описывает энергетический баланс жидкости перед сливным отвер-
стием и после него. Потенциальная энергия жидкости перед сливным
отверстием пропорциональна
h. При истечении из бака энергия жидко-
сти превращается в кинетическую энергию потока, пропорциональную
квадрату скорости
2
υ
. Приравнивая эти энергии, получаем hk
υ
υ
= .
Расход
F
пропорционален произведению скорости истечения на пло-
щадь сливного отверстия, откуда и следует (2.2-11).
Если бак имеет постоянную по высоте площадь поперечного сече-
ния
S , то
S
tV
ktF
)(
)(
= . (2.2-12)
Тогда из (2.2-9) и (2.2-10) получаем:
26
,
)(
)()(
)(
21
S
tV
ktFtF
dt
tdV
−+=
.
)(
)()()()}()({
2211
S
tV
ktCtFCtFCtVtC
d
t
d
out
−+=
Выберем в качестве базового режима установившееся состояние (ста-
тику), когда все величины являются постоянными -
0002010
,,,, VCFFF . При
этом из предыдущих уравнений получаем
02010
0 FFF
−
+
=
,
00202101
0 FCFCFC
−
+= .
S
V
kF
0
0
= .
При известных
10
F
и
20
F эти уравнения могут быть разрешены относи-
тельно
00
,VF и
0
C :
0
202101
0
2
2
0
020100
;;
F
FCFC
C
K
F
SVFFF
+
==+= .
Предположим теперь, что возникли отклонения от установившего-
ся состояния
)()(
1101
tFFtF Δ+= ,
)()(
2202
tFFtF
Δ
+=
и, как следствие,
.)()(
;)()(
),()(
0
0
0
tCCtC
tVVtV
tFFtF
out
Δ+=
Δ+=
Δ+=
Если эти отклонения невелики, то можно провести линеаризацию нели-
нейных дифференциальных уравнений объекта.
Сначала линеаризуем уравнение для полной массы
.
)(
)()()}()({
0
2201100
S
tVV
ktFFtFFtVtV
dt
d
Δ+
−Δ++Δ+=Δ+
Используем разложение нелинейной функции в ряд Тейлора и учтём,
что:

27
V
V
VV
dV
d
VV
Δ=Δ⋅
=
0
0
1
2
1
0
| .
Тогда
).(
2
)(
)()()(
0
0
220110
tR
V
tV
S
k
S
V
ktFFtFFtV +
Δ
⋅−−Δ++Δ+=Δ
&
Учитывая уравнение статики, и пренебрегая остаточным членом, полу-
чим:
).(
2
)()()(
0
21
tV
SV
k
tFtFtV Δ⋅−Δ+Δ=Δ
&
(2.2-13)
Введём параметр
0
0
F
V
=Θ
, называемый временем заполнения ба-
ка. Тогда, учитывая (2.2-12), получим
Θ
=
2
1
2
0
SV
k
. (2.2-14)
Кроме того, отметим, что
F
V
SV
Vk
Δ=
Θ
Δ
=
Δ
2
2
0
. (2.2-15)
Таким образом, вместо (2.2-13) запишем
).(
2
1
)()()(
21
tVtFtFtV Δ⋅
Θ
−Δ+Δ=Δ
&
(2.2-16)
Проведем аналогичные действия для уравнения баланса масс
растворённого вещества.
[][]
{}
[][][]
.
)(
)()()(
)()(
0
022021101
00
S
tVV
ktCCtFFCtFFC
tVVtCC
dt
d
Δ+
Δ+−Δ++Δ+=
=Δ+Δ+
После разложения в ряд Тейлора получим
).()(
2
)(
)()()()(
0
000
0
222021110100
tRtV
SV
kC
tC
S
V
k
S
V
kC
tFCFCtFCFCtVCtCV
−Δ−Δ−−
−Δ++Δ+=+
&
&

28
Учтём уравнения статики и отбросим остаточный член:
).(
2
)(
)()()()(
0
0
0
0
221100
tV
S
V
V
k
CtC
S
V
k
tFCtFCtVCtCV
Δ−Δ−
−Δ+Δ=+
&
&
Подставим в это уравнение
)(tV
&
из (2.2-16). Получим:
.)(
2
)()(
)(
2
)()()(
0
2010
0
022110
tV
C
tFCtFC
tV
C
tCFtFCtFCCV
Δ
Θ
−Δ−Δ−
−Δ
Θ
−Δ−Δ+Δ=Δ
&
Таким образом, в результате линеаризации мы получили систему
следующих дифференциальных уравнений, которые описывают процес-
сы в смесительном баке:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
Δ
−
+Δ
−
+Δ
Θ
−=Δ
Δ
Θ
−Δ+Δ=Δ
.)()()(
1
)(
)(
2
1
)()()(
2
0
02
1
0
01
21
tF
V
CC
tF
V
CC
tCtC
tVtFtFtV
&
&
(2.2-17)
На этом завершён для данного примера первый этап разработки -
составлено математическое описание объекта и в результате линеари-
зации получена его линейная модель. Далее это описание нужно пред-
ставить в удобной форме - в виде векторно-матричных дифференци-
альных уравнений и в виде структурной схемы.
Представим математическое описание объекта в виде
векторно-
матричных дифференциальных уравнений. Введем обозначения:
;
)(
)(
)(
⎥
⎦
⎤
⎢
⎣
⎡
Δ
Δ
=
tC
tV
tx
r
;
)(
)(
)(
2
1
⎥
⎦
⎤
⎢
⎣
⎡
Δ
Δ
=
tF
tF
tu
r
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Δ
Δ
Δ
=
V
C
F
ty )(
r
.
Теперь систему уравнений (2.2-17) можно записать в векторно-
матричном виде:
),()(
)()()(
txCty
tuBtxAtx
rr
r
r
&
r
=
+=
где:
29
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
Θ
−
Θ
−
=
1
0
0
2
1
A
;
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−−
=
0
02
0
01
11
V
CC
V
CC
B
;
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
Θ
=
01
10
0
2
1
C
.
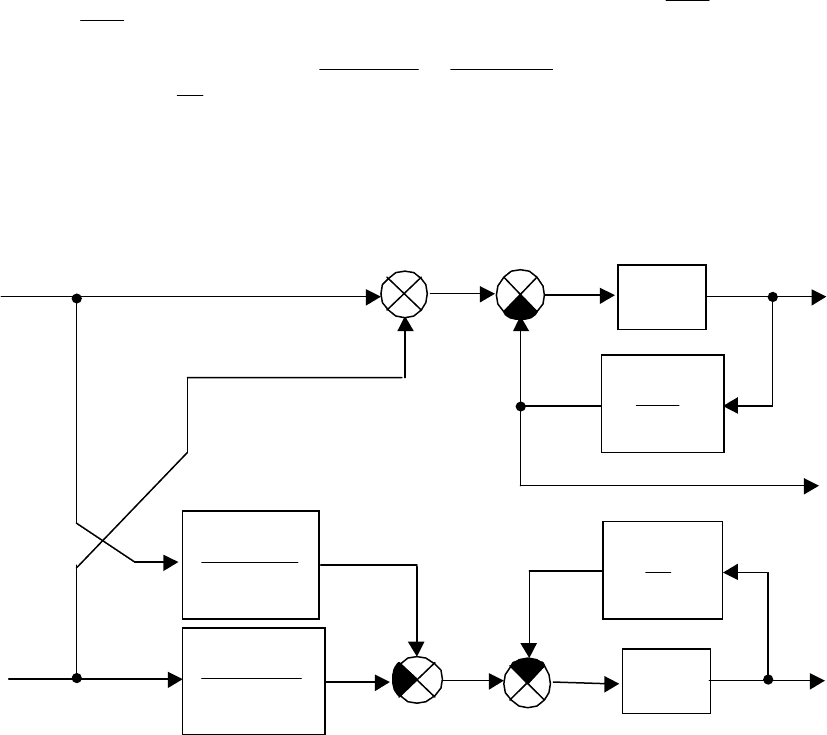
Структурная схема объекта представлена на рис.2 6
F
Δ
Рис. 2.6. Структурная схема смесительного бака как
объекта управления
VΔ
CΔ
0
01
V
CC −
0
20
V
CC −
2
FΔ
Θ
1
∫
1
FΔ
Θ2
1
∫
На основании полученных дифференциальных уравнений и струк-
турной схемы можно провести предварительный анализ свойств объекта
и сделать следующие выводы.
1. Изменение любой из входных переменных
1
F
Δ
и
2
F
Δ
приводит к од-
новременному изменению всех выходных переменных
V
Δ ,
F
Δ и C
Δ
.
Это особенно наглядно следует из наличия перекрёстных связей на
структурной схеме объекта.
2. При ступенчатом изменении любой из входных переменных каждая из
выходных переменных изменяется по экспоненциальному закону, при-
чём темп изменения концентрации
C
Δ
вдвое медленнее темпа изме-
нения объёма
V
Δ .
Предметом отдельного рассмотрения при проектировании системы
управления (СУ) должен стать анализ диапазонов изменения перемен-
ных объекта, в которых сохраняется адекватность линейной модели.
Прежде, чем закончить рассмотрение данного примера, имеет
смысл продемонстрировать некоторые последующие действия разра-
ботчика в части синтеза алгоритмов управления. Перед разработчиком

30
среди прочих встанут следующие две задачи. Одна из них - обеспечение
заданных требований по длительности и качеству процессов в системе,
то есть её динамических свойств. Рассмотрению соответствующих во-
просов посвящён третий раздел настоящего пособия.
Вторая задача - обеспечение возможности независимого управле-
ния объёмом и концентрацией. Введём понятие командных сигналов по
требуемым концентрации -
c
rΔ и объёму -
v
r
Δ
. В статике производные
всех переменных должны быть равны нулю, и как следует из структур-
ной схемы и дифференциальных уравнений объекта, должны выпол-
няться равенства:
0
2
1
21
=Δ⋅
Θ
−Δ+Δ
уст
VFF ;
0
1
2
0
20
1
0
01
=Δ
−
−Δ
−
+Δ
Θ
− F
V
CC
F
V
CC
C
уст
.
Отсюда, с учётом равенства
0
0
F
V
=Θ
, получаем
)(2
21
FFV
уст
Δ
+
ΔΘ=Δ ; (2.2-18)
2
0
20
1
0
01
F
F
CC
F
F
CC
C
уст
Δ
−
−Δ
−
=Δ . (2.2-19)
Для компенсации перекрёстных связей в объекте введём перекрё-
стные связи в регуляторе:
CCFVVF
raraF
Δ
+Δ
=
Δ
111
;
CCFVVF
raraF
Δ
+Δ
=
Δ
222
.
Подставим эти выражения в (2.2-18) и (2.2-19):
))()((2
2121 CCFCFVVFVFуст
raaraaV
Δ
+
+
Δ
+Θ=Δ ; (2.2-20)
.)(
)(
2
0
20
1
0
01
2
0
20
1
0
01
CCFCF
VVFVFуст
ra
F
CC
a
F
CC
ra
F
CC
a
F
CC
C
Δ
−
−
−
+
+
Δ
−
−
−
=Δ
(2.2-21)
Для того, чтобы установившееся значение объёма жидкости в баке
уст
VΔ определялось только командным сигналом
V
r
Δ
и не зависело от
C
rΔ , а выходная концентрация
уст
C
Δ
определялась только командным
