Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

51
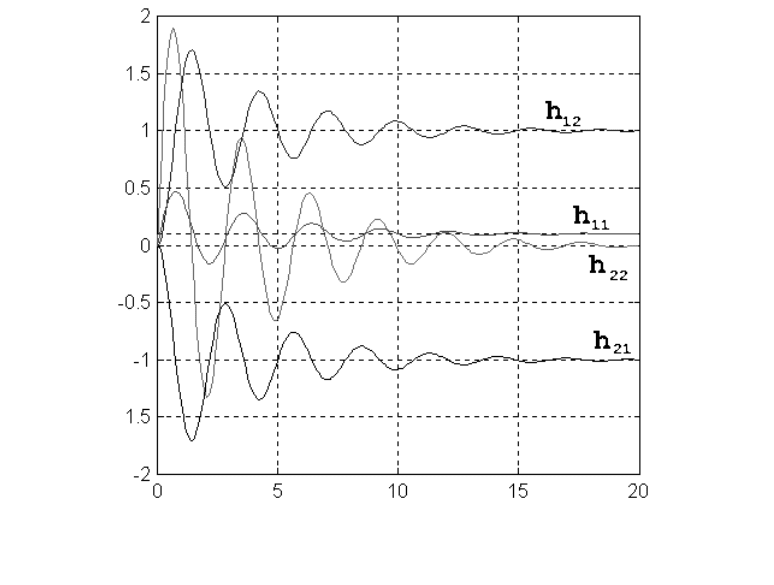
В качестве примера на рис. 2.12 изображены элементы матричной
переходной функции по вектору состояния для системы, представлен-
ной на рис. 2.11.
Рис.2.12. Элементы матричной переходной функции
д
ля системы, п
р
едставленной на
р
ис. 2.11
В стационарном случае рассмотренные матрицы являются функцией
одного аргумента:
()
(
)
(
)
(
)
BCBCewttwttw
A
yyy
τ
τ
τ
Φ
=
=
=−=
00
, (2.5-8)
и
() ( )
∫
−Φ=
t
y
BdtCtH
0
ττ
. (2.5-9)
Это выражение для переходной функции можно упростить. Производя
замену аргумента
τ
σ
−= t ,
получим
() ( )
∫
=
Φ=
0
t
y
BdCtH
σ
σσ
и окончательно
() ()
∫
Φ−=
t
y
BdCtH
0
ττ
. (2.5-10)
Используя представление переходной матрицы через матричную экспо-
ненту, можно получить
52
()
B
t
A
t
A
t
AEtCtH
y
⎭
⎬
⎫
⎩
⎨
⎧
++++=
K
!4!32
4
3
3
2
2
. (2.5-11)
Один из наиболее употребимых способов вычисления
()
tΦ и
(
)
tH со-
стоит в определении (расчете) соответствующих окаймленных матрич-
ных рядов.
ПРИМЕР 2.5-1.
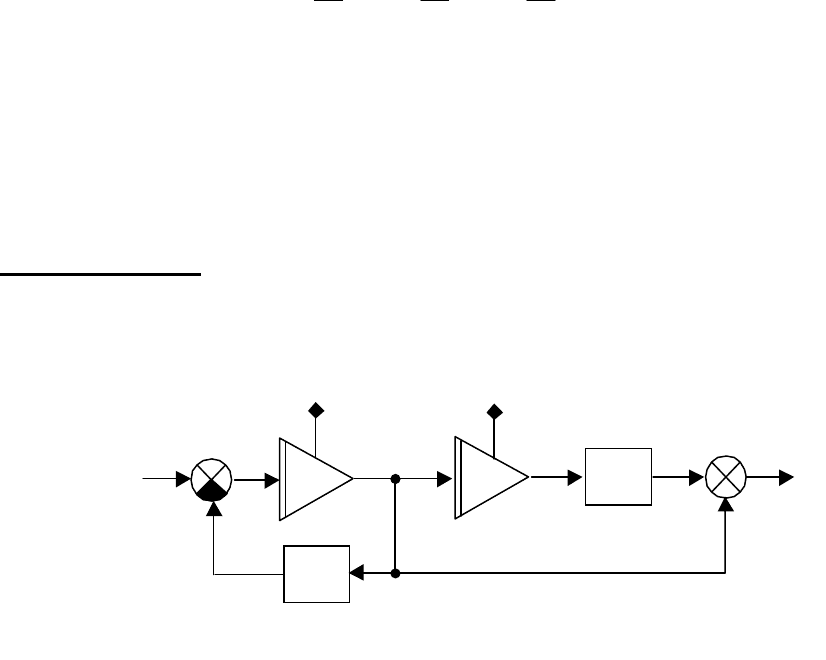
Объект управления задан системой дифференциальных
уравнений, которым соответствует схема в переменных состояния, при-
веденная на рис. 2.13.
Рис.2.13. Структурная схема к примеру 2.5-1
x
1
(0)
x
2
(0)
u
x
2
x
1
2
y
2
Этой схеме соответствуют уравнения
⎪
⎩
⎪
⎨
⎧
+=
+−=
=
.21
22
21
2
,2
,
xxy
uxx
xx
&
&
Требуется найти переходную матрицу, матричные весовую и переход-
ную функции, реакцию объекта на постоянный входной сигнал.
Прежде всего, найдем переходную матрицу. Элемент первой строки и
первого столбца этой матрицы можно определить как реакцию коорди-
наты
1
x на начальные условия
(
)
(
)
00,10
21
=
=
xx при 0=u . Решение
первого дифференциального уравнения дает
() ()
.1
111
=
= txt
ϕ
Аналогично
() ()
txt
222
=
ϕ
при
()
(
)
00,10
12
=== uxx .
Решая при этих условиях второе дифференциальное уравнение, полу-
чим
()
t
et
2
22
−
=
ϕ
.

53
Очевидно
()
0
21
=t
ϕ
, так как координата
2
x не зависит от
1
x . Для того,
чтобы определить
()
t
12
ϕ
, следует взять интеграл
()
()
t
t
edet
2
0
2
12
15.0
−−
−==
∫
τϕ
τ
.
Таким образом,
()
⎥
⎦
⎤
⎢
⎣
⎡
−
=Φ
−
−
t
t
e
e
t
2
2
0
15.01
)(
.
В соответствии с уравнениями объекта
[]
12;
1
0
;
20
10
=
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
−
= CBA
,
поэтому
()
1)(
=
Φ= BtCtw
y
и
() ( )
tBdCtH
t
y
=Φ=
∫
ττ
0
.
При нулевых начальных условиях и
constuu
=
=
0
()
tuty
⋅
=
0
.
Если начальные условия ненулевые, то
()
tuxxtuxtCty
⋅
+
+
=
+Φ=
0210
)0()0(2)(0)()(
r
.
При этом
()() ()() ()
()
()
()
()
()
()
.
1
2
1
1
4
1
2
1
0
01
2
1
0
0)(0)(
0
2
21
00
2
2
2
2
0
u
e
et
xe
xex
uBdxtutHxttx
t
t
t
t
t
x
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−+
+
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
−+
=
=⋅Φ+Φ=+Φ=
−
−
−
−
∫
ττ
rrr
Видно, что в выходной координате участвуют не все составляющие дви-
жения, присутствующие в векторе состояния. Еще более характерная
ситуация возникнет, если изменить исходные данные. Если положить

54
⎪
⎩
⎪
⎨
⎧
+−=
+=
=
21
22
21
2
2
xxy
uxx
xx
&
&
,
то поведение выходной координаты принципиально не изменится
tuxxty
⋅
+
+−=
021
)0()0(2)( ,
но процесс по координатам состояния будет неограниченно расти:
()
()
()
()
()
()
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−+
−−+−−
=
−
−
02
021
1
2
1
0
2
1
1
4
1
01
2
1
0
)(
22
22
uexe
tuexex
tx
tt
tt
r
.
Такие случаи, когда вектор выхода не отражает характерные свойства
объекта, могущие привести к катастрофическим результатам, будут
подробно обсуждаться в последующих разделах.
2.5.2. Модальная (спектральная) интерпретация решения векторно-
матричных дифференциальных линейных стационарных
уравнений
Рассмотрим сначала движение автономной системы
()
(
)
0
),( xtxtxAtx
r
r
r
&
r
== . (2.5-12)
Пусть все собственные числа матрицы
A
различны. Тогда ее собствен-
ные векторы
niv
i
,...,2,1,
=
r
образуют базис в пространстве
n
R
, то есть
являются линейно независимыми. В соответствии с (2.3-5) и (2.4-28)
решение уравнения (2.5-12) можно записать в виде
() ( )
∑
=
=
n
i
T
ii
t
xdvetx
i
1
0
r
r
r
r
λ
.
Обозначим скаляр
(
)
0xd
T
ii
r
r
=
μ
, (2.5-13)
тогда
()
.
1
∑
=
=
n
i
i
t
i
vetx
i
r
r
λ
μ
(2.5-14)
Очевидно, что свободное движение вектора состояния объекта является
комбинацией движений по собственным векторам матрицы
A
. Такие
движения называют модами системы, а матрицу собственных векторов
V - модальной матрицей. Коэффициент
i
μ
соответствует величине
возбуждения i - ой моды системы, обусловленной начальными условия-
55
ми. Иначе говоря, каждая мода возбуждается соответствующим выбо-
ром начального состояния.
Согласно (2.5-13),
[]
)0(...)0()0(
)0(
...
)0(
)0(
...
2211
2
1
21
ninii
n
iniii
xdxdxd
x
x
x
ddd +++=
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
μ
.
Если вектор начальных условий
)0(x
r
совпадает по направлению с i - м
собственным вектором, то есть
i
vx
r
r
⋅=
α
)0( ,
то, учитывая, что согласно (2.4-13) и (2.4-14),
0=
j
T
i
vd
r
r
при
j
i
≠
и
1=
i
T
i
vd
r
r
, получаем
.0)0()0( ijприxdиxd
T
jji
T
ii
≠====
r
r
r
r
μαμ
Таким образом, при указанном выборе начальных условий, возбуждает-
ся только i-ая мода, или «частота».
Рассмотрим с этих же позиций движение неавтономного объекта
).()()( tuBtxAtx
r
r
&
r
+=
Изложенный подход можно использовать и в этом случае, если вектор
)(tuB
r
разложить по собственным векторам матрицы
A
:
()
.)(
1
i
n
i
i
vttuB
r
r
×=
∑
=
β
. (2.5-15)
Для того, чтобы определить скалярные функции
)(t
i
β
, умножим обе
части этого равенства слева на
T
j
d
r
:
()
,)(
1
i
n
i
T
ji
T
j
vdttuBd
r
r
r
r
∑
=
=
β
откуда, учитывая (2.4-13) и (2.4-14), получаем
()
).(tuBdt
T
ii
r
r
=
β
(2.5-16)
Таким образом, в соответствии с формулой Коши (2.3-18) и выражением
для переходной матрицы (2.4-28) имеем

56
() ( )
()
()
()
()
()
()
()
.
0
0
1
0
0
11
0
1
∑
∫
∫
∑∑
∫
∑
=
−
==
−
=
−
⋅
⎭
⎬
⎫
⎩
⎨
⎧
+=
=+=
=⋅+=
n
j
j
T
j
t
tt
i
t
n
i
i
T
jji
n
j
t
At
t
n
i
ii
tAAt
vduBdee
dvdvexe
dvexetx
jj
j
rr
r
r
r
rr
rrr
ττμ
ττβ
ττβ
τλλ
τλ
τ
(2.5-17)
Если вынуждающая функция
)(tu
r
выбирается таким образом, чтобы
вектор
)(tuB
r
совпадал с направлением одного из собственных векторов
матрицы
A
, то она будет возбуждать только одну соответствующую мо-
ду «частоту».
2.6. Модели стационарных линейных систем в комплексной
плоскости на основе преобразования Лапласа
2.6.1. Матрица передаточных функций
Известно, что преобразование Лапласа определяется парой преобразо-
ваний
{}
()
()
{}
.)(
2
1
)(
,)()(
1
0
∫
∫
∞+
∞−
−
∞
−
⋅
==
==
jC
jC
pt
pt
dpepX
j
pXLtx
dtetxtxLpX
rr
r
rr
r
π
(2.6-1)
Первое из них называется прямым, а второе - обратным. Векторная
функция
)(tx
r
называется оригиналом, а )(pX
r
- изображением этого
оригинала по Лапласу;
p - комплексная переменная преобразования
Лапласа. Преобразование Лапласа можно осуществить, если
ω
σ
j
p += и
c
σ
σ
> , где
c
σ
- абсцисса абсолютной сходимости. Ве-
личина
C
σ
выбирается исходя из требования, чтобы функция
t
etx
σ
−
)(
r
при
C
σ
σ
> была абсолютно интегрируемой.
При вычислении обратного преобразования Лапласа интегрирование
ведется на плоскости комплексной переменной
p по прямой, парал-
лельной мнимой оси, лежащей на прямой
с, причем с выбирается так,
чтобы все полюсы
)(pX
r
оказались слева от прямой интегрирования
(рис. 2.14). На этом рисунке показано расположение полюсов некоторой
функции )(pX
r
.

57
Плоскость p
+j
c
σ
с
+
Рис.2.14. К вычислению обратного преобразования
Лапласа
Пусть, как обычно, уравнения объекта имеют вид
).()()(
);()()()()(
txtCty
tutBtxtAtx
rr
r
r
&
r
=
+=
Перейдем к изображениям по Лапласу
).()(
);()()0()(
pXCpY
pUBpXAxpXp
r
r
r
r
r
=
+=−
Перенесем
AX(p) в левую часть равенства, а )0(x
r
- в правую:
).()0()()( pUBxpXApE
r
r
r
+=−
Отсюда получаем выражение для изображения вектора состояния
)()()0()()(
11
pUBApExApEpX
r
r
r
−−
−+−= .
Сравнивая это равенство с формулой Коши
∫
⋅+⋅=
−
t
tAAt
duBexetx
0
)(
)()0()(
ττ
τ
rrr
,
отмечаем, что резольвента матрицы
A
может рассматриваться как изо-
бражение по Лапласу от переходной матрицы (матричной экспоненты):
{
}
At
eLApE =−
−1
)(
.
Справедливо равенство
,
)(
)(
)(
1
p
pI
ApE
A
ϕ
=−
−
(2.6-2)

58
где
)( p
I
- присоединенная матрица для матрицы А, и )(p
A
ϕ
- характе-
ристический полином матрицы
A
. )( p
I
и )(p
A
ϕ
могут быть определе-
ны по методу Фаддеева - Леверье.
При нулевых начальных условиях
),()()(
1
pUBApEpX
r
r
−
−= (2.6-3)
где функция
BApEpW
ux
⋅
−=
−1
)()( (2.6-4)
называется матричной передаточной функцией от вектора управления
до вектора выхода или передаточной функцией по каналу «u-x».
Аналогично, при нулевых начальных условиях
),()()(
1
pUBApECpY
r
r
−
−= (2.6-5)
где функция
BApECpW
uy
⋅
−
=
−1
)()( (2.6-6)
называется матричной передаточной функцией от вектора управления
до вектора выхода или передаточной функцией по каналу «u-y». Функ-
цию
1
)(
−
− ApE называют резольвентой матрицы
A
.
С использованием передаточной функции можно записать:
)()()(
)()()(
pUpWpY
pUpWpX
uy
ux
rr
r
r
⋅=
⋅=
. (2.6-7)
Принимая во внимание, что изображение по Лапласу
δ
- функции равно
единице, можно представить передаточную функцию как изображение
от весовой функции
{}
.)()( twLpW = (2.6-8)
Передаточная функция является функцией от матрицы
A
, поэтому в
соответствии с (2.4-27) можно записать
∑
=
−
⋅⋅
=
n
i
i
T
ii
uy
p
BdvC
pW
1
)(
)(
λ
r
r
(2.6-9)
и
∑
=
⋅
−
⋅⋅
=
n
i
i
T
ii
pU
p
BdvC
pY
1
)(
)(
)(
r
r
r
λ
. (2.6-10)
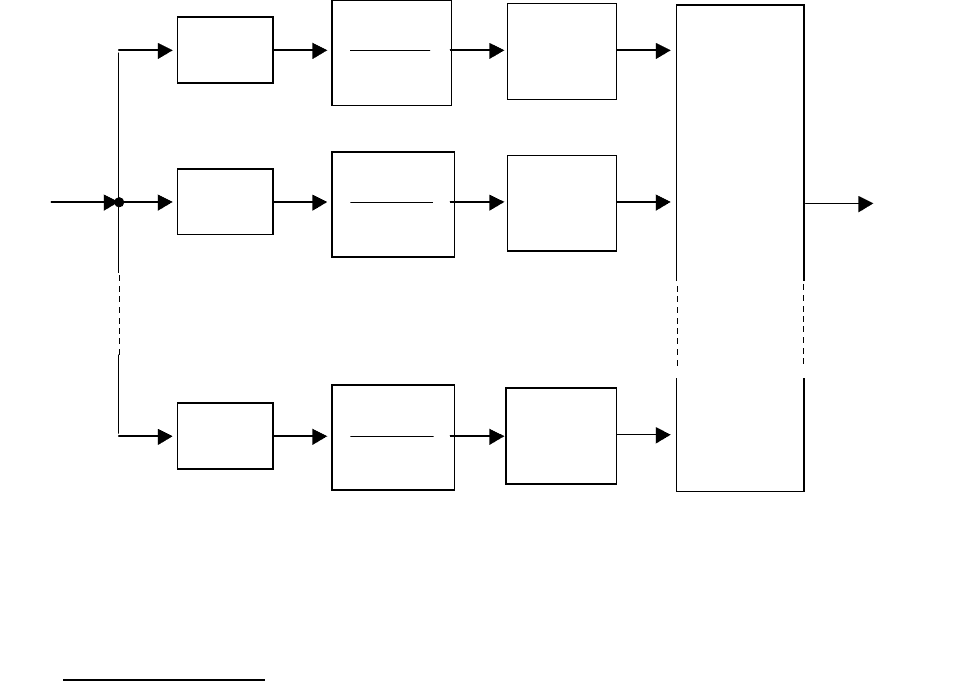
Графическое изображение последней формулы представлено в виде
структурной схемы, изображённой на рис. 2.15.
59
)(pY
r
)(pU
r
Bd
T
1
r
1
1
λ
−p
1
vC
r
Bd
T
2
r
2
1
λ
−p
2
vC
r
Bd
T
n
r
n
p
λ
−
1
n
vC
r
∑
Рис. 2.15. Структурная схема системы на базе представления
передаточной функции через собственные числа и собственные
векторы матрицы динамики
ПРИМЕР 2.6-1.
Для объекта, схема в переменных состояния кото-
рого приведена на рис.2.16, уравнения состояния имеют вид
;
;
;
223
132
121
uxx
uxx
uxx
+=
+=
−=
&
&
&
.
;
32
11
xy
xy
=
=
Им соответствует матрицы
.
100
001
;
10
01
01
;
010
100
010
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
= CBA
Характеристический полином имеет вид
λ
λ
λ
ϕ
−
=
3
)(
A
.
Собственные числа
1;1;0
321
−
=
==
λ
λ
λ
.
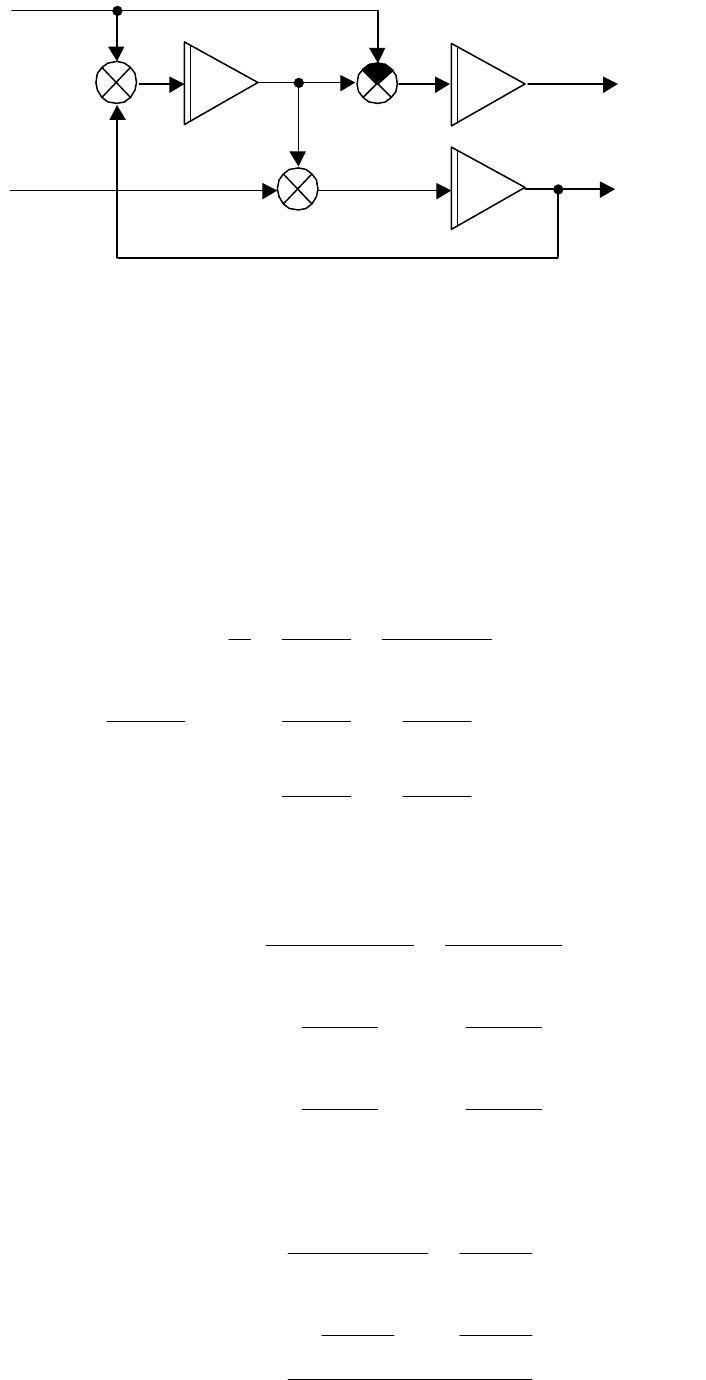
60
Рис.2.16. Структурная схема к примеру 2.6-1
y
2
y
1
u
1
u
2
x
3
x
2
x
1
Присоединенная матрица
()
.
0
0
11
2
2
2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
λλ
λλ
λλ
λ
I
Резольвента
()
()
()
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−
−−
−−
==−
−
11
1
0
1
1
1
0
)1(
1
1
11
22
22
22
1
λ
λ
λ
λλ
λ
λλλλ
λϕ
λ
λ
A
I
AE
.
В соответствии с (2.6-4) передаточная функция по вектору состояния
()
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−−
−−
−−
++−
=−=
−
11
1
1
1
1
)1(
1
)1(
1
)(
22
22
22
2
1
p
p
p
pp
p
pppp
pp
BApEpW
ux
и по вектору выхода
()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−−
−−
++−
=−=
−
11
1
1
1
)1(
1
)(
22
22
2
1
p
p
p
ppp
pp
BApECpW
uy
.
Используя присоединенную матрицу, можно найти матрицу правых соб-
ственных векторов
