Страшинин Е.Э. Основы теории автоматического управления. Часть I. Линейные непрерывные системы управления
Подождите немного. Документ загружается.

31
сигналом
C
rΔ и не зависела от,
V
r
Δ
, в равенстве (2.2-20) приравняем к
нулю коэффициент при
C
rΔ , а коэффициент при
V
r
Δ
приравняем к еди-
нице. В равенстве (2.2-21) приравняем к нулю коэффициент при
V
r
Δ
, а
коэффициент при
C
rΔ приравняем к единице. В результате решения
получившейся системы уравнений получим:
.;
;
2
1
;
2
1
21
0
2
21
0
1
21
01
2
21
20
1
CC
F
a
CC
F
a
CC
CC
a
CC
CC
a
CFCF
VFVF
−
−=
−
=
−
−
Θ
=
−
−
Θ
=
(2.2-22)
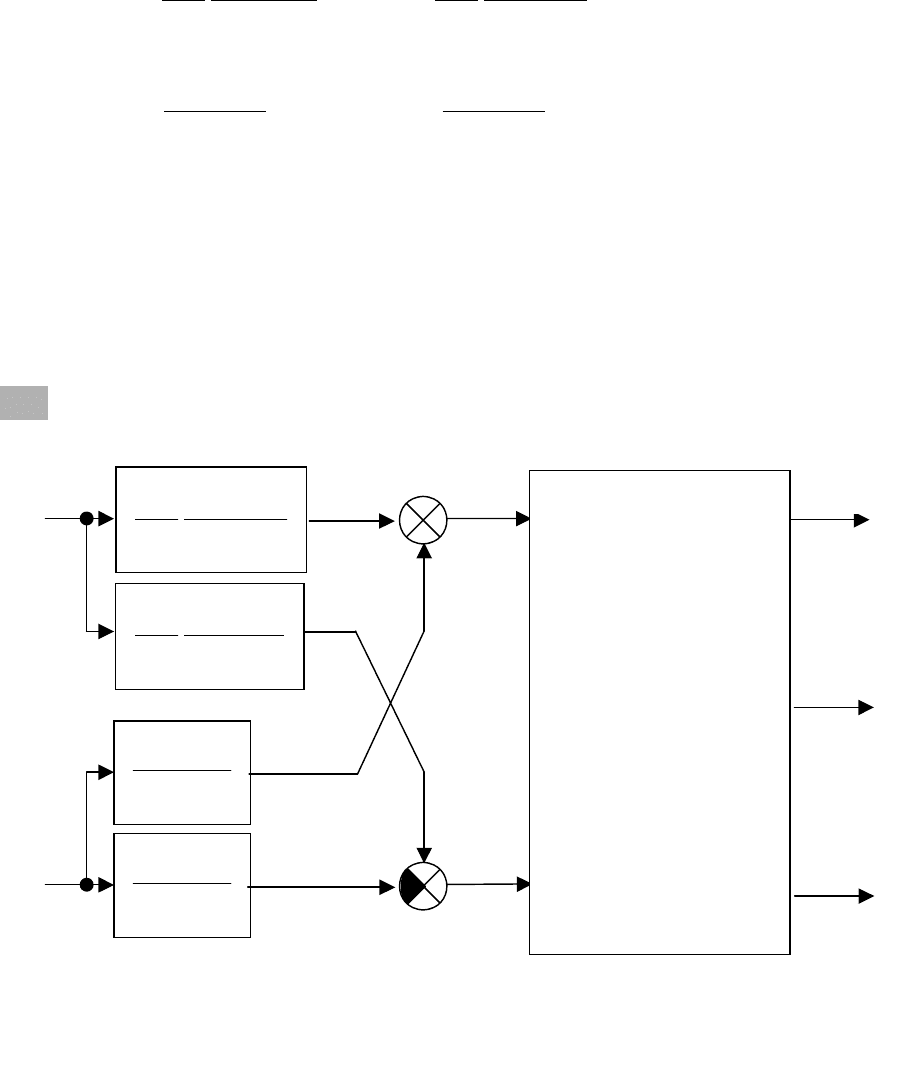
. В итоге получаем представленную на рис.2.7 структурную схему
системы управления смесительным баком, в которой обеспечена раз-
вязка каналов. Последнее означает, что командный сигнал
V
rΔ влияет
только на изменение объёма жидкости в баке, а командный сигнал
C
r
Δ
-
только на изменение концентрации. Объём жидкости в баке связан с
расходом выходного потока
F
Δ
коэффициентом пропорциональности
Θ2 , поэтому регулирование первого можно рассматривать как регули-
рование второго.
Рис. 2.7 Система управления смесительным баком
с развязанными каналами.
F
Δ
V
rΔ
21
20
2
1
CC
CC
−
−
Θ
C
rΔ
21
0
CC
F
−
21
0
CC
F
−
1
F
Δ
2
F
Δ
21
01
2
1
CC
CC
−
−
Θ
ОБЪЕКТ
VΔ
CΔ
32
2.3. Линейные системы, заданные обыкновенными диф-
ференциальными уравнениями в нормальной форме
Коши
2.3.1. Однородные дифференциальные уравнения
Рассмотрим, прежде всего, решение однородного векторно-матричного
дифференциального уравнения:
)()()( txtAtx
r
&
r
= , (2.3-1)
где каждому начальному условию
)(
0
tx
r
соответствует одно и только од-
но решение дифференциального уравнения. Будем полагать, что мат-
рица
)(t
A
непрерывна на промежутке ],0[
∞
∈
t . Множество всех реше-
ний образует n-мерное векторное пространство. Среди множества ре-
шений всегда может быть выбрано n линейно независимых.
Это может быть сделано следующим образом. Зададим начальные ус-
ловия
)(tx
i
r
, где ni ,,2,1 K= , совпадающие с базисными векторами
i
e
r
пространства
n
R
, то есть
ii
etx
r
r
=
)(
0
. Из свойства единственности
решений дифференциальных уравнений (через любую точку простран-
ства состояний проходит одна и только одна траектория) следует ли-
нейная независимость решений с указанными начальными условиями.
Матрица
[]
nn
tX
×
)( , столбцами которой являются n линейно независимых
решений системы (2.3-1), называется фундаментальной матрицей этой
системы дифференциальных уравнений.
Поскольку каждый столбец фундаментальной матрицы является реше-
нием системы (2.3-1), то фундаментальная матрица удовлетворяет
уравнению:
)()()( tXtAtX ⋅=
&
, при начальных условиях )(
00
tXX
=
. (2.3-2)
По определению в любой момент времени столбцы этой матрицы ли-
нейно независимы, значит ее определитель (определитель Вронского)
не равен нулю. на промежутке
],0[
∞
∈
t . Так как определитель матрицы
X
не равен нулю, то существует обратная матрица )(
1
tX
−
.
Матрица
)()(),(
0
1
0
tXtXtt
−
⋅
=Φ (2.3-3)
называется переходной матрицей уравнения (2.3-1) или переходной
матрицей, соответствующей матрице
)(t
A
. Переходная матрица явля-
ется определяющей при анализе и решении дифференциальных урав-
нений и собственно в теории управления. Поэтому ниже приводятся ос-

33
новные её свойства, в основном, непосредственно вытекающие из оп-
ределения этой матрицы.
1) Переходная матрица при совпадающих значениях первого и вто-
рого аргумента становится единичной матрицей:
EtXtXtttt
tt
=⋅=Φ=Φ
−
=
)()(),(),(
0
1
0000
0
.
2) При любых значениях аргументов
21
, tt переходная матрица
),(
21
ttΦ не вырождена и её определитель не равен нулю:
0),(
21
≠ttФ .
3) Обращение матрицы
),(
0
tt
Φ
эквивалентно изменению порядка
аргументов исходной матрицы:
[]
),()()()()(),(
0
1
0
1
0
1
0
1
tttXtXtXtXtt Φ=⋅=⋅=Φ
−
−
−−
.
4) Если в качестве фундаментальной матрицы начальных условий
принять единичную матрицу,
EtX
=
)(
0
то при всех прочих t пере-
ходная матрица будет совпадать с фундаментальной матрицей.
)(),(
0
tXttФ = . Но )(t
X
– это решение матричного дифференци-
ального уравнения (2.3-2). Поэтому переходная матрица может
быть определена как решение матричного дифференциального
уравнения:
),,()(),(
00
ttФtAttФ ⋅=
&
.),(
00
Ett
=
Φ
(2.3-4)
5) Переходная матрица определяет решение однородного векторно-
матричного дифференциального уравнения (2.3-1), удовлетво-
ряющее начальному условию
)()(
0
0
txtx
tt
r
r
=
=
:
)(),()(
00
txttФtx
r
r
⋅
= . (2.3-5)
Это действительно так, ибо, во-первых, при
0
tt
=
)()(),(
0000
txtxttФ
r
r
=
⋅ ,
во-вторых, с учетом свойства (4):
)()()(),()()(),()}(),({
000000
txtAtxttФtAtxttФtxttФ
dt
d
rrr
&
r
=== .
6) Из предыдущего свойства следует один из способов определения
переходной матрицы. Обозначим через
),(
0,
tt
ji
ϕ
элемент i-ой
строки и j-ого столбца переходной матрицы и запишем равенство
(2.3-5) в развернутом виде:
34
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⋅
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
)(
...
)(
...
)(
)(
),(...),(...),(),(
..................
),(...),(...),(),(
..................
),(...),(...),(
),(
),(...),(...),(),(
)(
...
)(
...
)(
)(
0
0
02
01
000201
000201
0202022021
0101012011
2
1
tx
tx
tx
tx
tttttttt
tttttttt
tttttttt
tttttttt
tx
tx
tx
tx
n
j
nnnjnn
inijii
nj
nj
n
i
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
,
откуда следует выражение для i-й координаты вектора состояния:
).(),()(),()(),()(
00,00,0101,
txtttxtttxtttx
nnijjiii
ϕ
ϕ
ϕ
+
+
+
+= KK
Если положить начальные условия по всем координатам вектора
стояния, кроме j-й, нулевыми, а по j-й - единичными, то есть
0)(
0
=tx
k
, при
j
knk
≠
= ,,2,1 K и 1
=
j
x , (2.3-6)
то элемент i-й строки и j-го столбца матрицы
),(
0
tt
Φ
можно опреде-
лить как процесс по i-й координате вектора состояния
).(),(
0,
txtt
iji
=
ϕ
(2.3-7)
7) К переходной функции применимо правило композиции:
).,(),(),(
011202
tttttt
Φ
⋅
Φ=Φ (2.3-8)
Действительно, решение уравнения (2.3-1) в момент t
1
при началь-
ных условиях
)(
0
tx
r
имеет вид:
).(),()(
0011
txttФtx
r
r
=
Если теперь этот результат принять за новые начальные условия,
то к моменту времени
2
t будем иметь:
).(),(),()(),()(
001121122
txttФttФtxttФtx
r
rr
⋅
==
8) Переходная матрица может быть вычислена с помощью ряда Пеа-
но, или матрицианта матрицы
A
:
,)))((())(()()(),(
0
K
+
⋅
⋅
+
⋅
+
+==Φ AQAQAQAQAQAQEAMtt
где
.)()(
0
ττ
dAAQ
t
t
∫
=
Для того, чтобы получить этот результат, проинтегрируем диффе-
ренциальное уравнение (2.3-1):

35
∫
+=
t
t
dxAtxtx
0
1110
)()()()(
τττ
rrr
.
Теперь повторим эту процедуру многократно, учитывая что:
.)()()()(
1
0
22201
∫
+=
τ
ττττ
t
dxAtxx
rrr
Тогда получим:
∫∫∫
∫∫∫
∫∫∫
+++=
=++
+++=
t
t
t
tt
t
t
tt
t
t
t
tt
txddAAdAE
txdddAAA
txddAAtxdAtxtx
00
1
0
2
00
1
0
00
1
0
)(...})()()({
...)()()()()()()(
)()()()()()()(
0122111
0123321
012210110
r
r
rrrr
τ
ττ
τ
ττττττ
ττττττ
ττττττ
Если объект – стационарный и матрица А состоит из постоянных и неза-
висящих от времени элементов, то матрициант матрицы А (или ряд
Пеано) превращается в выражение для матричной экспоненты:
.))(exp(
...
!3
)(
!2
)(
)(),(
)(
0
3
0
32
0
2
00
0
ttA
ettA
ttAttA
ttAEttФ
−
=−=
=+
−
+
−
+−+=
(2.3-9)
Очевидно, что в стационарном случае переходная матрица является
уже функцией только одного аргумента, равного разности начального и
текущего (конечного) времени:
.)(),(
00
tA
etttt
Δ
=
−Φ=Φ (2.3-10)
Переходная матрица для стационарного объекта обладает рядом до-
полнительных замечательных свойств, трансформирующихся из соот-
ветствующих свойств переходной матрицы для нестационарного объек-
та :
из 1) -
E
Ф =)0( ; (2.3-11)
из 3) -
tA
etФtФ
Δ⋅−−
=
Δ−=Δ )()(
1
; (2.3-12)
из 4) -
=+
−
+
−
++=
−
...
!3
)(3
!2
)(2
0
)(
2
0
3
0
2
0
ttAttA
A
dt
ttdФ
AeeAttФA
ttAttA
⋅
=
⋅
=
−⋅=
−− )()(
0
00
)( ; (2.3-13)
36
из 5) - решение однородного дифференциального уравнения имеет
вид:
)()(
0
)(
0
txetx
ttA
r
r
⋅
=
−
; (2.3-14)
из 7) -
)()( tФtkФ
k
Δ
⋅=Δ⋅ . (2.3-15)
2.3.2. Решение неоднородных векторно-матричных дифференци-
альных уравнений
Ранее были получены выражения для определения решений одно-
родного дифференциального уравнения нестационарной:
)(),()(
00
txttФtx
r
r
⋅
= (2.3-5)
и стационарной
)()(
0
)(
0
txetx
ttA
r
r
⋅
=
−
(2.3-14)
систем. Используем эти результаты для определения решения неодно-
родного линейного векторно-матричного уравнения, соответствующего
(2.2-7):
)()()()( tutBtxtAx
r
r
&
r
⋅+⋅= . (2.3-16)
Произведем замену:
)(),()(
0
tzttФtx
r
r
⋅
= (2.3-17)
и продифференцируем это выражение:
=⋅+⋅= )(),()(),()(
00
tzttФtzttФtx
&
r
r
&
&
r
)(),()(),()(
00
tzttФtzttФtA
&
r
r
⋅+⋅⋅= .
Сопоставляя это выражение с предыдущим, получим
)()()(),(
0
tutBtzttФ
r
&
r
⋅=⋅ ,
откуда
)()(),()(
0
tutBttФtz
r
&
r
⋅⋅= ,
или, интегрируя,
∫
⋅+=
t
t
duBtФtztz
0
)()(),()()(
00
ττττ
rrr
.
Из (2.3-17) видно, что
)()(
00
txtz
r
r
= .

37
В итоге получаем выражение для решения векторно-матричного линей-
ного неоднородного дифференциального уравнения, известное под на-
званием формулы Коши
∫
+⋅=
t
t
duBtФtxttФtx
0
)()(),()(),()(
00
ττττ
rrr
. (2.3-18)
2.4. Некоторые сведения из теории матриц
2.4.1. Собственные числа, характеристический полином, присоеди-
ненная матрица
Умножение квадратной матрицы
A
на некоторый вектор
x
r
дает новый
вектор
z
r
, который, в общем случае, иначе ориентирован в пространстве
и имеет другую длину по сравнению с исходным вектором. Однако, су-
ществуют и такие векторы, которые при выполнении этой операции ме-
няют только свою длину, но не меняют направления, то есть
,vvA
r
r
λ
= (2.4-1)
где
λ
- это вещественная или комплексная скалярная величина, назы-
ваемая собственным значением (характеристическим числом) матрицы
A
, а вектор v
r
называется собственным вектором этой матрицы. В раз-
вёрнутом виде уравнение (2.4-1) имеет следующий вид:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=+++
=+++
=+++
nnnnnn
nn
nn
vvavava
vvavava
vvavava
λ
λ
λ
K
KKKKKKKKKKKKK
K
K
1211
22122121
11112111
.
Очевидно, что для существования ненулевых
i
v необходимо выполне-
ние условия:
0)det(
=
−
≡− AEAE
λ
λ
. (2.4-2)
Это уравнение называют характеристическим, или вековым уравнением
матрицы
A
. Левая часть этого уравнения называется характеристичес-
ким полиномом, которая является степенным полиномом от λ, и степень
его равна размеру n матрицы
A
.
nn
nnn
A
AE
α
λ
α
λ
α
λ
α
λ
λ
λ
ϕ
+
+
+
+
+=−=
−
−−
1
1
2
2
1
1
||)( K . (2.4-3)
Таким образом, каждая квадратная матрица
A
имеет n собственных
значений
,,2,1
,
n
λ
λ
λ
K , которые могут быть определены путём решения
38
характеристического уравнения с использованием стандартного матема-
тического обеспечения на цифровых вычислительных машинах.
Алгебраическая кратность корня
λ
– это его кратность как корня харак-
теристического уравнения.
Геометрическая кратность корня
λ
– это количество линейно независи-
мых решений уравнения (2.4-2), или количество линейно независимых
векторов
v
r
, связанных с данным
λ
.
Если
λ
не является собственным значением матрицы
A
, то существует
матрица
1
)(
−
− AE
λ
. По правилу определения обратных матриц
AE
I
AE
−
=−
−
λ
λ
λ
)(
)(
1
, (2.4-4)
где )(
λ
I
называется присоединённой матрицей для матрицы
A
. Ее
элементы определяются как алгебраические дополнения элементов
матрицы
T
AE )( −
λ
. Здесь символ Т означает транспонирование. При-
соединённая матрица - это матричный полином степени n-1:
12
2
1
1
)(
−−
−−
+
+
++=
nn
nn
IIIEI
λ
λ
λ
λ
K , (2.4-5)
где
E
– единичная матрица
[
]
nn
×
.
Если все собственные числа матрицы
A
различны, то собственные век-
торы матрицы
A
могут быть выбраны пропорциональными любым не-
нулевым столбцам матрицы
niI
i
,...,2,1,)(
=
λ
.
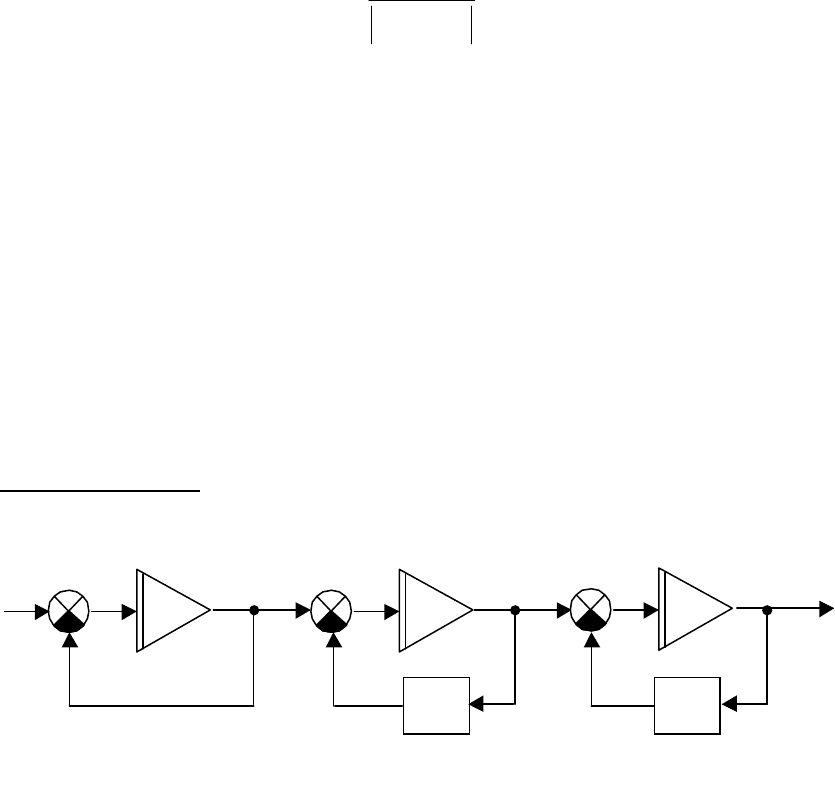
ПРИМЕР 2.4-1.
Пусть объект задан структурной схемой, приведённой на
рис.2.8.
u
x
1
x
2
x
3
32
Рис.2.8. Структурная схема к примеру 2.4-1
Ему соответствует система уравнений
211
3 xxx +−=
&
;
322
2 xxx
+
−=
&
;
uxx +−=
33
&
,
или в матричном виде

39
)()()( tButxAtx +=
r
&
r
,
где
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
100
120
013
A
;
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
1
0
0
B
.
Для этих исходных данных получаем характеристический полином
6116
100
120
013
)(
23
+++=
+
−+
−+
=
λλλ
λ
λ
λ
λ
P .
Ему соответствуют собственные числа
.3,2,1
321
−=−=−=
λλλ
Найдем присоединенную матрицу
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
++
+++
+
++
=
)2)(3(00
3)1)(3(0
11)1)(2(
)(
λλ
λλλ
λ
λ
λ
λ
I
=
.
600
330
112
500
140
013
2
3
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
+
λλ
E
Найдём собственные векторы матрицы
A
:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
000
000
122
)(;
000
110
110
)(;
200
200
100
)(
321
λλλ
III
и можно выбрать
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
0
0
1
;
0
1
1
;
2
2
1
321
vvv
rrr
.
Полученный результат нетрудно проверить прямой подстановкой в (2.4-
1).
Имеется ряд алгоритмов для определения коэффициентов характери-
стического полинома и присоединенной матрицы. Один из наиболее

40
употребимых - это алгоритм Фаддеева - Леверье. Он состоит в сле-
дующей последовательности вычислений:
A
1
=A; α
1
=−
1
SpA ; I
1
=A
1
+α
1
E;
A
2
=AI
1
;
2
1
2
−=
α
2
SpA ; I
2
=A
2
+α
2
E;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
A
n-1
=AI
n-2
;
1
1
1
−
−=
−
n
n
α
1−n
SpA ; I
n-1
=A
n-1
+α
ν−1
E;
A
n
=AI
n-1
;
n
n
1
−=
α
n
SpA ; I
n
=A
n
+
n
α
E=0;
Здесь через
SpA обозначен след матрицы
A
, то есть сумма ее диаго-
нальных элементов:
∑
=
=
n
i
ii
aSpA
1
.
Последнее равенство процедуры используется для контроля точности
вычислений.
Для объекта, приведенного в примере 2.4-1,
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
−
=
600
060
006
;
500
380
119
32
AA .
Если матрица
A
не вырожденна, то из промежуточных результатов ал-
горитма Фаддеева - Леверье, учитывая, что
,EA
nn
α
−=
получаем
1
1
1
−
−
−=
n
n
IA
α
. (2.4-6)
Для рассматриваемого примера
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
−
600
330
112
6
1
1
A .
