Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.


Глава 4
ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Оптические свойства газов определяют перенос энергии излучением, а также такие свой-
ства неравновесной среды, как коэффициент усиления лазерной активной смеси и дру-
гие фотопроцессы. Рассмотрим вначале различные элементарные процессы излучения
и поглощения света, затем уравнение переноса энергии излучением в газе.
4.1 Элементарные процессы излучения и поглощения света
Процессы излучения и поглощения света связаны с изменением энергии атомной систе-
мы, которое определяется переходами электрона в дискретном или непрерывном спек-
тре. Процессы перехода могут быть представлены на энергетической диаграмме, где
связанное состояние соответствует отрицательной, а свободное – положительной энер-
гии электрона. Переходы могут происходить в непрерывном спектре, когда электрон
является свободным и совершает переходы в поле атома или иона. Такие переходы на-
зываются свободно-свободными (free-free) переходами. Переходы могут быть связанно-
свободными (bound-free), или свободно-связанными (free-bound), когда одно из состоя-
ний принадлежит непрерывному спектру, а второе, дискретному спектру, и переходы
могут происходить в дискретном спектре (bound-bound), когда начальное и конечное
состояния принадлежат дискретному спектру.
4.1.1 Cвободно-свободные переходы
Возможны два типа переходов, связанных с излучением и поглощением света. Первый
тип – тормозное излучение. Рассмотрим процесс, в котором электрон, имеющий ско-
рость v
0
, рассеивается на частице A (атоме, ионе или молекуле) и переходит в состояние
с другой скоростью v, при этом излучается квант ¯hω:
e(v
0
) + A → e(v) + A + ¯hω. (4.1)
В соответствии с законом сохранения энергии в этом процессе
mv
0
2
2
=
mv
2
2
+ ¯hω.
81

82 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Сечение тормозного излучения определяется, как и при рассеянии частиц, отношением
вероятности процесса к потоку падающих частиц:
dσ
v
0
,v,ω
=
dW (v
0
, v, ω)
n
e
v
0
. (4.2)
Вероятность излучения dW (v
0
, v, ω) может быть вычислена по классической или по
квантовой теории. Обратный процесс является процессом тормозного поглощения.
Если электрон, пролетая в поле атома, поглощает квант света, то он приобретает энер-
гию, большую первоначальной. Соответственно сечение рассеяния определяется отно-
шением вероятности процесса к потоку падающих частиц и к потоку квантов, падаю-
щих на систему. Поток квантов вводится следующим образом. Пусть u
ω
– спектральная
плотность энергии или фотонов, так что u
ω
dω – энергия фотонов. Если эту энергию
поделить на энергию фотонов ¯hω, то получится количество фотонов в единице объема
(концентрация квантов) в интервале частот от ω и до ω + dω:
n
ω
=
u
ω
dω
¯hω
. (4.3)
Умножив эту концентрацию квантов на скорость света, получим поток квантов cu
ω
dω/¯hω.
4.1.2 Связанно-свободные переходы
К связанно-свободным переходам относятся: фоторекомбинация и фотоионизация.
При фоторекомбинации электрон, имеющий скорость v, взаимодействует с ионом A
+
,
захватывается и образует атом A в состоянии n с излучением кванта ¯hω:
e(v) + A
+
→ A
n
+ ¯hω. (4.4)
Из закона сохранения энергии следует
mv
2
2
= −E
n
+ ¯hω, (4.5)
где E
n
– отрицательная энергия связанного состояния атома. Сечение фоторекомбина-
ции определяется отношением вероятности процесса к потоку падающих электронов:
dσ
v,n,ω
=
dW (v, n, ω)
n
e
v
. (4.6)
Обратный процесс называется фотоионизацией. При падении кванта с энергией ¯hω на
атом в состоянии n выбивается электрон, который приобретает скорость v и образуется
ион:
A
n
+ ¯hω → e(v) + A
+
. (4.7)
Закон сохранения энергии для фотоионизации имеет вид
¯hω = −E
n
+
mv
2
2
. (4.8)
Сечение фотоионизации определяется отношением вероятности рассеяния к потоку па-
дающих квантов:
dσ
nω,v
=
dW (n, ω, v)
cu
ω
dω/¯hω
. (4.9)
4.2. КЛАССИЧЕСКАЯ ТЕОРИЯ ТОРМОЗНОГО ПОГЛОЩЕНИЯ 83
4.1.3 Cвязанно-связанные переходы
Следующий, третий, тип процессов – это связанно-связанные переходы. Они бывают
двух типов: переходы с излучением в линиях, при котором вначале атом находится в
верхнем состоянии n, затем переходит в низшее состояние m с излучением кванта ¯hω и
с поглощением в линиях – при обратном переходе из низшего в верхнее состояние под
действием излучения:
A
n
→ A
m
+ ¯hω, (n > m), (4.10)
A
m
+ ¯hω → A
n
, (n > m). (4.11)
Под дискретным спектром могут пониматься электронные уровни в атомах, молекулах
или колебательные, вращательные состояния молекул. В последнем случае происхо-
дят колебательно-вращательные переходы, образуя спектры поглощения и излучения
для молекул. Эти спектры являются "полосатыми" вследствие того, что колебательно-
вращательные уровни находятся близко друг к другу по сравнению с характерными
температурами в нагретом газе. Рассмотрим последовательно элементарные процессы
излучения и поглощения света.
4.2 Классическая теория тормозного поглощения
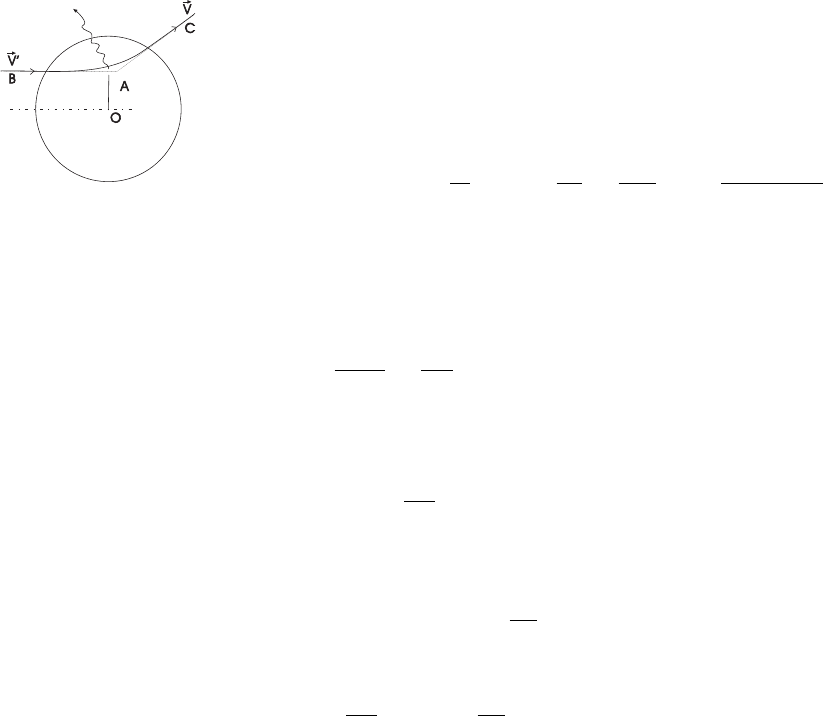
ÒðàåêòîðèÿBAC-èìïóëüñíîåïðèáëèæåíèå
Рис. 4.1: Тормозное излучение (а – область
действия потенциала)
Из классической теории поля известна форму-
ла для интенсивности излучения в дипольном
приближении. Интенсивность I, или количе-
ство энергии ∆E, излучаемой в единицу вре-
мени в процессе с изменением дипольного мо-
мента системы определяется формулой
dI =
1
c
3
|
¨
d × n|
2
do
4π
=
|
¨
d|
2
c
3
sin
2
ϑ
2π sin ϑdϑ
4π
,
где n – единичный вектор, проведенный в точ-
ку наблюдения, а d =
P
i
e
i
r
i
– дипольный мо-
мент системы. Интегрируя по телесному углу,
получаем
I =
d∆E
dt
=
2
3c
3
|
¨
d|
2
.
Интегрируя по времени, найдем полную энергию, излучаемую электроном при пролете
около рассеивающего центра:
∆E =
Z
∞
−∞
2
3c
3
|
¨
d|
2
dt.
Эта потеря энергии может быть разложена в интеграл Фурье с использованием теоремы
Парсeваля:
Z
∞
−∞
|f(t)|
2
dt = 2
Z
∞
0
|f
ω
|
2
dω
2π
, (4.12)
или для потери энергии излучением:
∆E =
4
3c
3
Z
∞
0
|
¨
d
ω
|
2
dω
2π
.

84 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Последнее выражение можно представить в виде
∆E =
Z
∞
0
∆E
ω
dω,
где спектральная плотность излучаемой энергии равна:
∆E
ω
=
2e
2
3πc
3
w
2
ω
,
где w
ω
– фуpье-компонента ускорения электрона. Для точного решения задачи необ-
ходимо найти уравнение для траектории электрона, затем ускорение электрона вдоль
траектории и вычислить спектральную плотность энергии излучения. Такая задача для
рассеяния электрона в поле иона рассматривается, например, в курсе теоретической
физики Ландау и Лифшица [14]. Однако здесь мы используем более простое, так на-
зываемое импульсное приближение, при котором гладкая траектория изменения скоро-
сти заменяется на импульсную, т.е. с мгновенным изменением скорости в одной точке
– наименьшего расстояния между налетающим электроном и рассеивающим центром.
Изменение скорости в импульсном приближении имеет вид
∆v ≈ 2v sin
ϑ
2
.
С другой стороны, оно по определению равно ∆v =
R
wdt =
R
aδ(t)dt = a, следова-
тельно, в импульсном приближении вектор ускорения имеет вид w = ∆vδ(t), а его
фурье-компонента
w
ω
=
Z
∞
−∞
w(t)e
iωt
dt =
Z
∞
−∞
∆vδ(t)e
iωt
dt = ∆v.
Соответственно спектральная плотность излучения в этом приближении равна
∆E
ω
=
2e
2
3πc
3
(∆v)
2
=
2e
2
3πc
3
(2v sin
ϑ
2
)
2
=
4e
2
v
2
3πc
3
(1 − cos ϑ).
Величина ∆E
ω
dω представляет энергию, излученную в интервале частот ω, ω + dω при
рассеянии электрона на атоме с прицельным параметром ρ. Для нахождения излучения
электронами, налетающими на различных прицельных расстояниях, необходимо умно-
жить спектральную потерю энергии на вероятность рассеяния электронов и проинте-
грировать ее по всем прицельным расстояниям. В результате получим излучательную
способность газа:
ε
ω
=
Z
n
e
v∆E
ω
dσ. (4.13)
Здесь n
e
vdσ(v, ϑ) – вероятность рассеяния электрона на угол ϑ. В теории излучения
вводится понятие дифференциального излучения q
ω
, которое представляет количество
энергии, излучаемой в интервале частот ω, ω + dω единичным потоком электронов при
рассеянии на атоме ε
ω
= n
e
vq
ω
:
q
ω
=
Z
∆E
ω
dσ. (4.14)
С учетом выражения для ∆E
ω
получаем
q
ω
dω =
4
3π
Ã
e
2
¯hc
!
µ
v
c
¶
2
σ
m
d¯hω, (4.15)
4.2. КЛАССИЧЕСКАЯ ТЕОРИЯ ТОРМОЗНОГО ПОГЛОЩЕНИЯ 85
где введено транспортное сечение рассеяния электронов на тяжелых частицах:
σ
m
=
Z
(1 − cos ϑ)dσ. (4.16)
Найдем энергию, излучаемую потоком электронов n
e
v, пролетающих на всех расстоя-
ниях:
ε
ω
=
Z
n
e
vdσ(v, ϑ)∆E
ω
= n
e
vσ
m
4e
2
v
2
3πc
3
.
Это выражение можно представить в виде
ε
ω
= n
e
vq
ω
,
где q
ω
=
R
∆E
ω
dσ – дифференциальное излучение, или энергия, излученная в процессе
при единичном потоке электронов, рассеивающихся на одной частице. Для рассеяния
электронов на ионах, когда для σ
m
можно использовать формулу Резерфорда, получа-
ется:
q
ω
=
4e
2
v
2
3πc
3
π
Ã
2Ze
2
mv
2
!
2
ln
χ
max
χ
min
,
где χ
max
и χ
min
– максимальный и минимальный углы рассеяния. Как уже упоминалось,
максимальный угол рассеяния порядка π, т.е. χ
max
∼ 1, а минимальный угол рассеяния
равен отношению амплитуды рассеяния f к прицельному расстоянию ρ
ω
, на котором
излучается квант с частотой ω ∼ v/ρ
ω
, где амплитуда кулоновского рассеяния или длина
Ландау
f =
2Ze
2
mv
2
.
Используя выражение для амплитуды рассеяния, получаем отношение максимального
и минимального углов рассеяния:
χ
max
χ
min
=
ρ
ω
f
=
mv
3
2Ze
2
ω
,
соответственно дифференциальное излучение имеет вид:
q
ω
=
16e
6
3c
3
Z
2
m
2
v
2
ln
mv
3
2Ze
2
ω
. (4.17)
Эта формула справедлива при малых значениях частот ω, много меньших, чем ω
1
=
mv
3
/2Ze
2
. При более точном решении задачи без использования импульсного прибли-
жения (см., например, [13]) оказывается, что это приближение справедливо только для
мягких квантов. Для жестких квантов ω À ω
1
решение было получено Крамерсом, оно
справедливо для параболических траекторий, в то время как предыдущее рассмотре-
ние было справедливо для гиперболических траекторий. Приближение Крамерса да-
ет результат, отличающийся численным множителем и отсутствием логарифмического
множителя:
q
ω
=
16πe
6
Z
2
3
√
3m
2
c
3
v
2
. (4.18)
Эта формула для спектрального излучения может быть представлена в следующем без-
размерном виде:
q
ω
dω =
8π
3
√
3
αZ
2
r
0
f
T
µ
v
T
v
¶
2
d¯hω, (4.19)

86 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
где α = e
2
/¯hc – постоянная тонкой структуры, r
0
= e
2
/mc
2
– классический радиус
электрона. Формулы (4.18) и (4.19) содержат две расходимости, которые называются
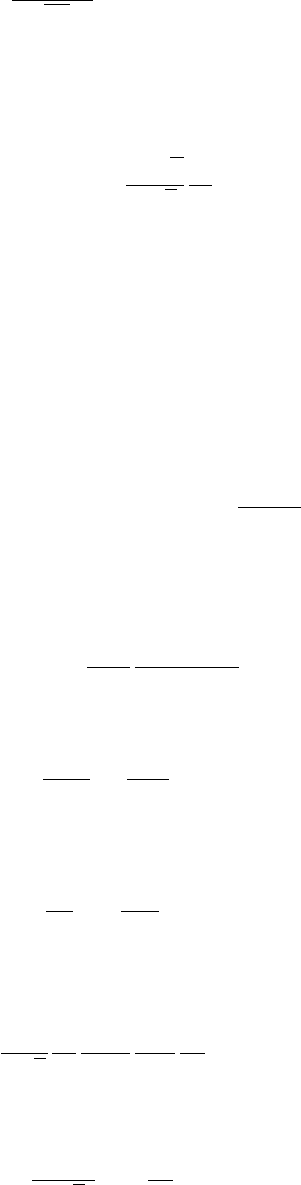
инфракрасной и ультрафиолетовой катастрофами. Зависимость q
ω
от ω приведена на
рис. 4.2.
Рис. 4.2: Зависимость дифференциального излучения от частоты для тормозного процесса
Инфракрасная катастрофа связана с расходимостью q
ω
при ω → 0. Она устраняется
тем, что мягкие кванты излучаются при больших прицельных расстояниях, которые в
плазме ограничены дебаевским радиусом соотношением ω
min
= v/r
D
.
Ультрафиолетовая катастрофа связана с тем, что интеграл по частотам, представля-
ющий полную излученную энергию, расходится, т.к. на больших частотах q
ω
= const.
Расходимость дифференциального излучения по частотам возникает вследствие класси-
ческого описания процесса. При квантовом описании следует учесть, что максимально
излучаемая энергия не может превышать начальную кинетическую энергию электрона,
т.е. возникает ограничение по частотам, ¯hω
max
= mv
2
/2. Поэтому интегрирование следу-
ет вести не до бесконечности, а до частоты ω
max
= mv
2
/2¯h. Излучательная способность
газа представляет энергию, которая излучается в единице объема газа в единицу време-
ни в единицу телесного угла. Таким образом, ε
T
ω
dω – энергия, излучаемая в интервале
частот от ω, до ω + dω в тормозных процессах. Используем приближение Крамерса, т.к.
жесткие кванты дают больший вклад в энергетический баланс излучения. Тогда усред-
нение по максвелловскому распределению электронов по скоростям дает следующий
результат для дифференциального излучения:
vq
ω
=
n
i
n
e
4πv
T
16πe
6
Z
2
3
√
3m
2
c
3
v
2
T
Z
∞
x
min
4
√
π
e
−x
2
xdx,
а для излучательной способности
ε
T
ω
dω =
1
4π
n
i
n
e
Z
∞
v
min
vq
ω
f(v)dv,
где нижний предел интегрирования по скорости v
min
=
q
2¯hω/m. Распределение Макс-
велла имеет вид
f(v)dv =
µ
m
2πkT
¶
3/2
e
−mv
2
/2kT
=
4
√
π
e
−x
2
x
2
dx,
4.2. КЛАССИЧЕСКАЯ ТЕОРИЯ ТОРМОЗНОГО ПОГЛОЩЕНИЯ 87
где x
2
= mv
2
/2kT . В результате получаем излучательную способность газа при тормоз-
ных процессах при рассеянии электронов на ионах в следующем виде:
ε
T
ω
dω =
4(Ze)
2
3
√
3π¯hc
n
i
n
e
v
T
f
T
r
0
d(¯hω)e
−¯hω/kT
, (4.20)
где f
T
= e
2
/kT – "тепловая" амплитуда рассеяния. Полная энергия, излучаемая в тор-
мозных процессах при рассеянии электронов на ионах, может быть получена интегриро-
ванием по частоте и по телесному углу. В результате получается следующее выражение:
ε
T
= 4π
Z
∞
0
ε
T
ω
dω =
16
√
π
3
√
3
e
2
¯hc
n
i
n
e
v
T
f
T
r
0
kT, (4.21)
или в практических единицах:
ε
T
= 4 .49(n
e
/10
18
)(T/10
3
)
1/2
(Вт/см
3
).
Обратный процесс тормозного поглощения найдем, используя принцип детального рав-
новесия. Для реакции
e(v‘) + A
+
→ e(v) + A
+
+ ¯hω
он имеет следующий вид:
n
i
n
e
f(v
0
)dv
0
v
0
q
ω
dω = n
i
n
e
f(v)dvv
cu
ω
dω
¯hω
σ
ωv,v
0
¯hω, (4.22)
где u
ω
– спектральная плотность энергии излучения, cu
ω
dω/¯hω – поток фотонов. Спек-
тральная плотность энергии излучения в равновесном газе имеет вид, который будет
получен ниже:
u
ω
=
¯hω
3
π
2
c
3
1
e
¯hω/kT
− 1
,
закон сохранения энергии для тормозного излучения имеет вид
mv
0
2
2
=
mv
2
2
+ ¯hω.
Подставляя эти выражения в уравнение детального баланса 4.22, находим сечение тор-
мозного поглощения
σ
ωv,v
0
=
v
0
2
v
2
π
2
c
2
q
ω
¯hω
3
³
1 − e
−¯hω/kT
´
.
С использованием формулы Крамерса для дифференциального излучения получим се-
чение этого процесса:
σ
ωv,v
0
=
16π
3
6
√
3
e
2
¯hc
2Ze
2
mv
2
Ze
2
mc
2
c
2
ω
3
³
1 − e
−¯hω/kT
´
,
или в безразмерном виде
σ
ωv,v
0
=
8Z
2
π
3
3
√
3
αr
0
f
c
2
ω
3
³
1 − e
−¯hω/kT
´
. (4.23)
88 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
Выражение в скобках представляет поправку на индуцированное излучение. Коэффи-
циент тормозного поглощения на ионах можно получить усредняя сечение по функции
распределения частиц:
κ
ω
= n
i
n
e
vσ
ωv,v
0
= n
i
n
e
Z
vσ
ωv,v
0
f(v)dv.
В общем случае коэффициент поглощения излучения также имеет вид
κ
ω
= κ
0
ω
³
1 − e
−¯hω/kT
´
,
где κ
0
ω
– "истинный" коэффициент поглощения. После интегрирования коэффициент
поглощения можно представить в виде
κ
0
ω
= n
i
n
e
Z
f(v)vdv
8π
3
3
√
3
r
0
Ã
2Ze
2
mv
2
!
αc
2
ω
3
.
Выполняя интегрирование, получаем
κ
0
(i)
ω
= 2
r
π
3
αn
i
n
e
πf
2
4
3
π
µ
v
T
ω
¶
3
. (4.24)
Эта формула также называется формулой Крамерса.
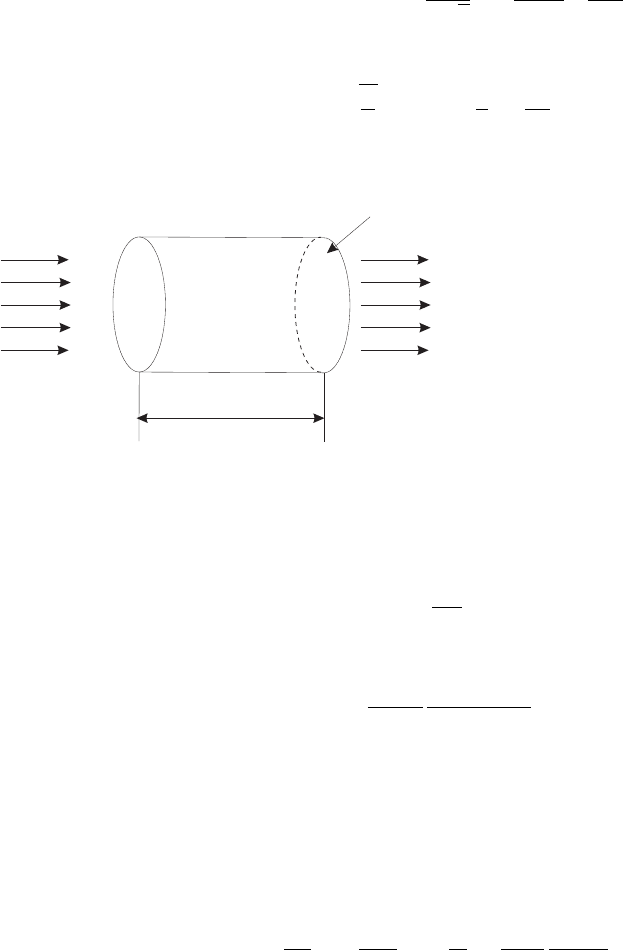
dx
I d
w
w
(I +d
w
I d
w
) w
S
Рис. 4.3: Изменение потока излучения вдоль пути
Приведем другой способ вывода
коэффициента поглощения излуче-
ния κ
ω
, также основанный на рас-
смотрении детального баланса в рав-
новесном газе. Рассмотрим в среде,
в которой распространяется излу-
чение, некоторый элементарный ци-
линдр длиной dx, сечением S на ко-
торый падает излучение B
ω
d
ω
(рис.
4.3). В состоянии равновесия
κ
0
ω
dxB
ω
dωS = ε
ω
dωSdx.
Из этого равенства получаем, что коэффициент поглощения излучения определяется
формулой Кирхгофа, т.е. равен отношению интенсивности излучения к интенсивности
излучения черного тела:
κ
0
ω
=
ε
ω
B
ω
,
где интенсивность излучения абсолютно черного тела
B
ω
=
¯hω
3
4π
3
c
2
1
e
¯hω/kT
− 1
, (4.25)
которая связана с плотностью энергии излучения соотношением B
ω
= cu
ω
/4π.
4.2.1 Тормозное поглощение при рассеянии электронов на атомах
Без учета поправки на индуцированные переходы выражение для сечения индуциро-
ванного тормозного излучения имеет вид
σ
ωv,v
0
=
v
0
2
v
2
π
2
c
2
q
ω
¯hω
3
=
Ã
v
0
v
!
2
π
2
c
2
¯hω
3
4e
2
v
0
2
3πc
3
σ
m
.

4.3. ФОТОРЕКОМБИНАЦИЯ 89
Это выражение можно представить в виде
σ
ωv,v
0
=
Ã
v
0
v
!
4
4π
3
Ã
e
2
¯hc
!
v
2
ω
3
σ
m
.
Отношение квадрата скоростей следует из закона сохранения энергии:
Ã
v
0
v
!
2
= 1 +
2¯hω
mv
2
.
Отсюда находим коэффициент поглощения излучения
κ
0
ω
= n
e
n
a
< vσ
ωv,v
0
>=
= n
e
n
a
4π
3
Ã
e
2
¯hc
!
Z
∞
0
v
Ã
1 +
2¯hω
mv
2
!
v
2
T
ω
3
σ
m
4
√
π
x
2
e
−x
2
dx,
или
κ
0
ω
= n
e
n
a
4
3
π
µ
v
T
ω
¶
3
e
2
¯hc
4
√
π
Z
∞
0
µ
1 +
u
x
2
¶
x
5
e
−x
2
σ
m
(x)dx,
где u = ¯hω/kT , или в практических единицах
κ
0
ω
= αn
e
n
a
σ
m
4
3
π
µ
v
T
ω
¶
3
F (u), (4.26)
где F (u) – интеграл с множителем 4/
√
π. Сравнивая коэффициенты излучения при
рассеянии электронов на атомах с коэффициентами излучения при рассеянии электро-
нов на ионах, находим их отношение, которое оказывается пропорциональным частотам
столкновений электронов с атомами и ионами:
κ
(a)
ω
κ
(i)
ω
=
F (u)
2
q
π/3
n
a
n
i
σ
m
πf
2
'
ν
ea
ν
ei
. (4.27)
4.3 Фоторекомбинация
Рассмотрим процесс фоторекомбинации, для которого из закона сохранения энергии
следует:
¯hω =
mv
2
2
− E
n
.
Примем квазиклассическое приближение, согласно которому фоторекомбинация на
верхние, близко расположенные уровни описывается как тормозное излучение в область
энергий с шириной ∆E, где эта величина определяется как среднее расстояние между
уровнями атома по формуле:
∆E =
dE
n
dn
.
Для атома водорода уровни энергии определяются формулой E
n
= −I/n
2
, где I – по-
тенциал ионизации атома водорода I = e
2
/2me
4
= 13.6 эВ. В этом случае ∆E = 2I/n
3
.
Дифференциальное излучение фоторекомбинации определяется формулой, аналогич-
ной тормозному излучению:
90 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ
q
n
= q
ω
∆Eδ
Ã
¯hω + E
n
−
mv
2
2
!
, (4.28)
где δ-функция выражает закон сохранения энергии, ее размерность обратно пропорци-
ональна энергии. Для q
ω
используем формулу Крамерса
q
ω
=
8π
3
√
3
Z
2
α¯hr
0
f
T
1
x
2
, (4.29)
где x
2
= mv
2
/2kT . После этого выполним следующие операции:
1. усреднение по максвелловскому распределению электронов,
2. интегрирование по частотам,
3. суммирование фоторекомбинации на различные дискретные уровни n.
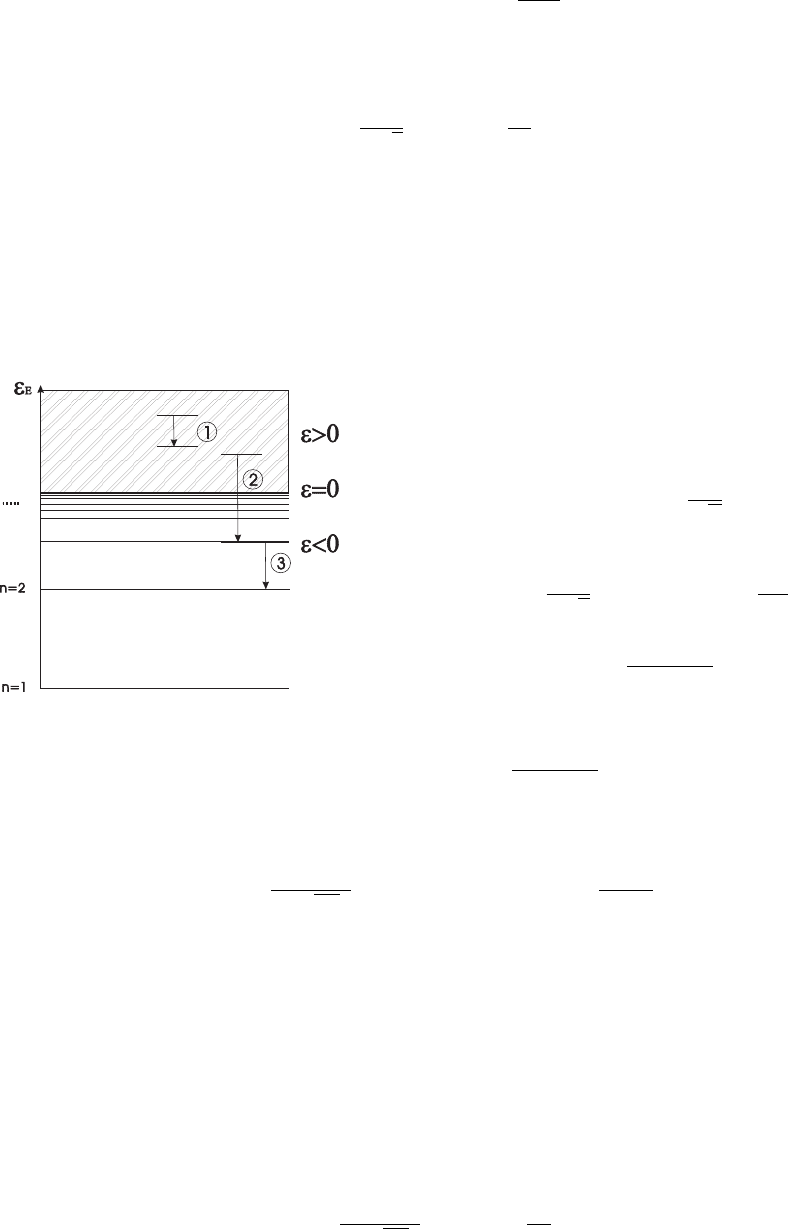
Рис. 4.4: Фоторекомбинация электрона на
дискретный уровень атома
Усреднение по максвелловскому распределению
электронов Излучательная способность газа
при фоторекомбинации на уровень n определя-
ется следующим выражением:
ε
ω,n
(T ) = n
e
n
i
Z
∞
0
vq
n
4
√
π
x
2
e
−x
2
dx,
или
ε
ω,n
(T ) =
32π
3
√
3
αZ
2
n
e
n
i
v
T
r
0
f
µ
I
kT
¶
¯h×
×
Z
∞
0
2xe
−x
2
δ
Ã
¯hω + E
n
kT
− x
2
!
dx.
Принимая во внимание, что
Z
∞
0
e
−x
2
δ
Ã
¯hω + E
n
kT
− x
2
!
dx
2
= e
−¯hω/kT −E
n
/kT
,
получаем окончательно излучательную способность газа при фоторекомбинации на уро-
вень n:
ε
ωn
(T )dω =
32παZ
2
3
√
3π
n
e
n
i
v
T
r
0
fe
−¯hω/kT −E
n
/kT
I
kT n
3
d¯hω. (4.30)
Размерность излучательной способности газа эрг/см
3
сек или Вт/м
3
.
4.3.1 Интегрирование по частотам
При интегрировании по частотам следует принять во внимание, что при рекомбинации
на уровень n излучаются частоты в интервале −E
n
< ¯hω < ∞:
ε
n
=
Z
∞
¯hω
min
=−E
n
ε
ωn
dω.
В результате интегрирования получаем
ε
n
=
32παZ
2
3
√
3π
n
e
n
i
v
T
r
0
f
I
n
3
. (4.31)
