Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.

4 ЗАДАНИЕ 3. УСТОЙЧИВОСТЬ ТЕЧЕНИЙ ГАЗА И ЖИДКОСТИ 57
и.т.д. Постоянные A
1
, A
2
, B
1
, B
2
найдем из гранич-
ных условий:
u(0) =
1
(π
2
+ κ
2
)
2
µ
A
1
+
4πd
π
2
+ κ
2
¶
= 0
Du(0) =
1
(π
2
+ κ
2
)
2
(κB
1
+ A
2
+ π) = 0
u(1) =
1
(π
2
+ κ
2
)
2
µ
A
1
cosh κ + B
1
sinh κ + A
2
cosh κ + B
2
sinh κ −
4πd
π
2
+ κ
2
¶
= 0
Du(1) =
1
(π
2
+ κ
2
)
2
"
A
1
κ sinh κ+B
1
κ cosh κ+A
2
(cosh κ+κ sinh κ)+
+B
2
(sinh κ + κ cosh κ) − (1 + d)π
#
= 0
Решая эту систему уравнений, находим коэффици-
енты: A
1
= −
4πd
π
2
+κ
2
. Обозначим ∆ = sinh
2
κ − κ
2
A
2
= −
π
∆
·
sinh κ(sinh κ − κ) − dκ sinh κ +
4dκ
π
2
+ κ
2
(1 + cosh κ)(κ + sinh κ)
¸
B
1
=
π
∆
·
κ − sinh κ − d sinh κ +
4d
π
2
+ κ
2
(κ + sinh κ)(1 + cosh κ)
¸
B
2
=
π
∆
·
(sinh κ − κ)(cosh κ + 1) − d(κ cosh κ − sinh κ) +
4dκ sinh κ
π
2
+ κ
2
(κ + sinh κ)
¸
Подставим в (7)
R
1
0
(7) sin πxdx :
−
1
T κ
2
Z
1
0
sin πx(D
2
−κ
2
) sin πxdx =
Z
1
0
˜u(x) sin πxdx
Z
1
0
sin πx(D
2
− κ
2
) sin πxdx = −
π
2
+ κ
2
2
Подставляя ˜u(x), получаем:
(π
2
+ κ
2
)
3
2κ
2
T
= J
1
A
1
+J
2
B
1
+J
3
A
2
+J
4
B
2
+J
5
+
4πd
π
2
+ κ
2
J
6
(9)
J
1
=
Z
1
0
cosh κx sin πxdx =
π(cosh κ + 1)
κ
2
+ π
2
J
2
=
Z
1
0
sinh κx sin πxdx =
π sinh κ
κ
2
+ π
2
J
3
=
Z
1
0
x cosh κx sin πxdx =
dJ
2
dκ
=
π
κ
2
+ π
2
µ
cosh κ −
2κ sinh κ
κ
2
+ π
2
¶
J
4
=
Z
1
0
x sinh κx sin πxdx =
dJ
1
dκ
=
π
κ
2
+ π
2
µ
sinh κ −
2κ(cosh κ + 1)
κ
2
+ π
2
¶
J
5
=
Z
1
0
(1+dx) sin
2
πxdx =
1
2
+
d
4
; J
6
=
Z
1
0
cos πx sin πxdx = 0.
Подставляя в (9), получаем:
(π
2
+ κ
2
)
3
2κ
2
T
=
1
2
+
d
4
+
π
2
(F
(0)
+ F
(Θ)
)
π
2
+ κ
2
F
(0)
=
1
π
(
(1+cosh κ)A
(0)
1
+sinh κB
(0)
1
+
µ
cosh κ −
2κ sinh κ
π
2
+ κ
2
¶
A
(0)
2
+
+
·
sinh κ −
2κ(1 + cosh κ)
π
2
+ κ
2
¸
B
(0)
2
)
A
(0)
1
= 0; B
(0)
1
=
1
∆
(κ−sinh κ); A
(0)
2
= −
sinh κ
∆
(sinh κ−κ)
B
(0)
2
=
1
∆
(sinh κ − κ)(cosh κ + 1)
F
(0)
=
1
∆
(
sinh κ(κ−sinh κ)−
µ
cosh κ −
2κ sinh κ
π
2
+ κ
2
¶
sinh κ(sinh κ−κ)+
·
sinh κ −
2κ(1 + cosh κ)
π
2
+ κ
2
¸
×
×(sinh κ−κ)(cosh κ+1)
)
= −
4κ(sinh κ − κ)(1 + cosh κ)
∆(π
2
+ κ
2
)
A
(d)
1
= −
4
π
2
+ κ
2
, A
(d)
2
=
1
∆
·
κ sinh κ −
4κ
π
2
+ κ
2
(1 + cosh κ)(κ + sinh κ)
¸
B
(d)
1
=
1
∆
·
4(κ + sinh κ)(1 + cosh κ)
π
2
+ κ
2
− sinh κ)
¸
; B
(d)
2
=
1
∆
·
4κ sinh κ(κ + sinh κ)
π
2
+ κ
2
+ sinh κ −κ cosh κ
¸
.
F
(0)
= −
4(1 + cosh κ)
π
2
+ κ
2
+
sinh κ
∆
·
4(κ + sinh κ)(1 + cosh κ)
π
2
+ κ
2
− sinh κ
¸
+
+
1
∆
µ
cosh κ −
2κ sinh κ
π
2
+ κ
2
¶·
κ sinh κ −
4κ
π
2
+ κ
2
(1 + cosh κ)(κ + sinh κ)
¸
+
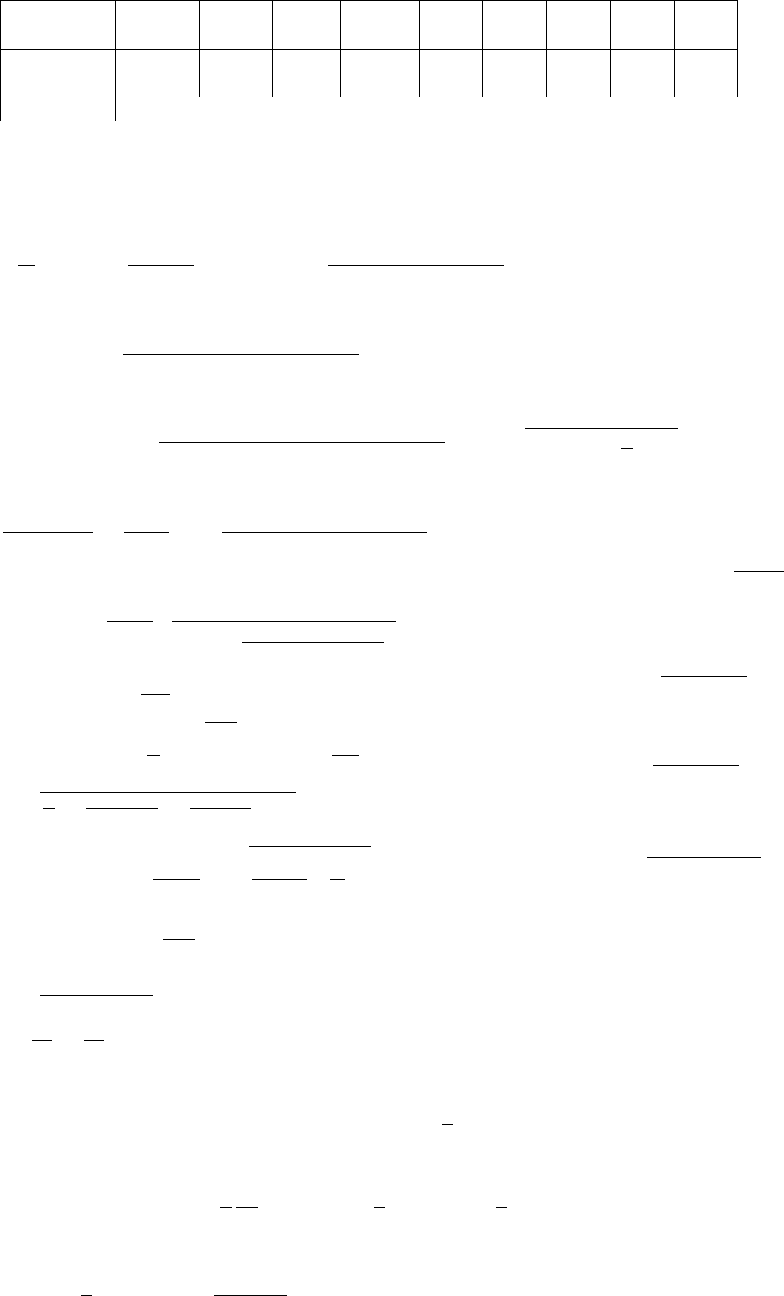
5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 58
µ −0, 99 −0, 9 −0, 5 −0, 25 0 0, 25 0, 5 0, 9 0, 99
, hline T
kp
343000 34300 6860 4573 3430 2744 2287 1805 1724
Re
1
6863 1574 792 709 686 709 792 1574 6863
, hline Re
2
-6794 -1417 -396 -177 0 177 396 1417 6794
, hline
Таблица 13:
+
1
∆
·
sinh κ −
2κ
π
2
+ κ
2
(1 + cosh κ)
¸
·
·
4κ sinh κ(κ + sinh κ)
π
2
+ κ
2
+ sinh κ −κ cosh κ
¸
=
=
2κd(cosh κ + 1)(κ − sinh κ)
∆(π
2
+ κ
2
)
F
(0)
+ F
(d)
= −
2κ(2 + d)(1 + cosh κ)(sinh κ − κ)
∆(π
2
+ κ
2
)
(π
2
+ κ
2
)
3
2κ
2
T
=
d + 2
4
·
1 −
8κπ
2
(2 + d)(1 + cosh κ)
(π
2
+ κ
2
)
2
(sinh κ + κ)
¸
; d+2 = 1+µ
T =
2
1 + µ
·
(π
2
+ κ
2
)
3
κ
2
h
1 −
16π
2
κ cosh
2
κ/2
(π
2
+κ
2
)
2
(κ+sinh κ)
i
Получаем T =
1
1+µ
f(x) Функция f (x) имеет вид:
Получаем T
kp
=
3430
1+µ
По определению числа
Тейлора T = 2
¡
d
R
¢
3
Re
2
1
(1 − µ), µ =
Re
2
Re
1
.
Эксперимент (лаб.раб. N26):
R
d
=
R
1
+R
2
2(R
2
−R
1
)
=
3+3,5
2(3,5−3)
= 6, 5 >> 1
Re
1
=
Ω
1
R
2
ν
=
s
1715
1 − µ
2
µ
R
d
¶
3
Re
2
= µRe
1
, T =
3430
1+µ
Составим таблицу значений
первого приближения:
Линии тока: Определяется по функции тока
dr
u
r
=
dz
u
z
; udz − wdx = 0; Ψ =
Z
u
r
dz − u
z
dr
u(x, z) = u(x) cos kz; w(x, z) = w(x) sin kz; w = −
1
κ
Du
Ψ =
Z
u(x) cos kzdz+
Z
1
κ
du
dx
sin kzdxd =
1
k
sin kzu(x)+
1
k
u(x) sin kz =
=
2
k
sin kzu(x) =
2Ω
1
x
2
d
2
νk
· 2˜u(x) sin kz
Рис. 15:
˜
Ψ =
Ψ(π
2
+ κ
2
)
2
4Re
1
(kd)
¡
d
R
¢
2
· d
= (π
2
+κ
2
)˜u(x) sin kz = const.
˜
˜u(x) = (π
2
+ κ
2
)˜u(x)
Ограничимся случаем d =
Ω
2
−ω
1
Ω
1
= 0 (Re
1
= Re
2
)
или µ = 1. Наиболее неустойчивые возмущения со-
ответствуют κ ' 3, 12. При этом: A
1
= 0,
A
2
= −
π sinh κ
sinh κ + κ
' −2, 46
B
1
=
−π
sinh κ + κ
' −0, 22
B
2
=
π(cosh κ + 1)
sinh κ + κ
= 2, 69
Получаем
˜
˜u = sin πx + x(2, 69 sinh 3, 12x −
2, 46 cosh 3, 12x) − 0, 22 sinh 3, 12x Получаем u
r
=
const ·
˜
˜u(x) cos kz, u
z
= −(d
˜
˜u/dx) sin kz
5 Задание 4. Турбулентное
движение высокотемпера-
турных сред)
4.1 Показать, что для однородной изотопной тур-
булентности в несжимаемой среде корреляцион-
ная функция скалярной величины и скорости рав-
на нулю < tanh eta
0
v
0
i
>= 0, а корреляционная
функция скоростей определяется только продоль-
ной корреляционной функцией.
Решение
5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 59
1. Корреляционная функция B
i
(x, r) =<
tanh eta
0
(x)v
i
(x + r) > для однородной
изотропной турбулентности имеет вид:
B
i
(r) =< tanh eta
0
(0)v
i
(r) >= r
i
f(r)
Из условия несжимаемости
∂B
i
∂r
i
= f(r) + r
i
df
dr
·
r
i
r
= f(r ) + r
df
dr
= 0
Решение этого уравнения
df
f
= −
dr
r
; lnf = ln
c
r
, f >
c
r
Из граничного условия |f (0)| < ∞ следует c =
0, т.е.
< tanh eta
0
(0)v
i
(r) >= 0
2. B
ij
(r) =< v
i
(x)v
j
(x+r) > для однородной изо-
тропной турбулентности
B
ij
(r) = C(r)
r
i
r
j
r
2
+ D(r)δ
ij
Рассмотрим систему координат с осью x
вдоль r = M
˜
M, M(x), tildeM(x + r), тогда
B
LL
(r) =< v
L
(0)v
L
(r) > - продольная корре-
ляционная функция
B
NN
(r) =< v
n
(0)v
n
(r) > - поперечная кор-
реляционная функция. Выразим C и D через
D
LL
, D
NN
.
B
LL
= C + D, D
NN
= D, .
B
ij
(r) = (B
LL
− B
NN
)
r
i
r
j
r
2
+ B
NN
δ
ij
Из уравнения непрерывности для несжимае-
мой жидкости получаем:
∂B
ij
∂r
j
=< v
i
(0)
∂v
j
(r)
∂r
j
>= 0
Дифференцируя B
ij
, получим:
B
NN
=
µ
1 +
r
2
d
dr
¶
B
LL
(r)
т.е. любая компонента B
ij
выражена через
B
LL
.
4.2. Найти асимптотическое изменение (при
t → ∞) интегрального масштаба турбулентного
движения на стадии распада турбулентности для
однородной изотропной турбулентности.
Решение
Уравнение Кармана-Ховарта имеет вид
∂B
LL
∂t
=
1
2
4
∂
∂r
r
4
µ
B
LL,L
+ 2ν
∂B
LL
∂r
¶
На стадии распада турбулентности, когда B
LL,L
=
0, находим
∂B
LL
∂t
= 2ν
1
r
4
∂
∂r
r
4
∂B
LL
∂r
это уравнение теплопроводности в 5-мерном про-
странстве, его решение
B
LL
(r, t) =
1
(8πνt)
5/2
Z Z
∞
−∞
Z Z Z
B
LL
(r
0
, 0)exp
"
−
5
X
i=1
(r
i
− r
0
i
)
2
8νt
#
dr
0
1
...dr
0
5
Интегрируя по угловым переменным (см.ниже),
получаем
B
LL
(r, t) =
1
4νtr
3/2
Z
∞
0
B
LL
(r
0
, 0)r
05/2
I
3/2
µ
rr
0
4νt
¶
exp
µ
−
r
2
+ r
02
8νt
¶
dr
0
В пределе t → ∞ заменяя модифицированную
функцию Бесселя I
3/2
(x) ее первым членом при
x → ∞, находим
B
LL
(r, t) =
Λ
48
√
2π(νt)
5/2
e
−
r
2
8νt
где Λ - инвариант Лойцянского, Λ =
R
∞
0
r
4
B
LL
(r, t)dr. Кинетическая энергия тур-
булентности убывает по закону
< u
2
>= B
LL
(0, t) =
Λ
48
√
2π(νt)
5/2
а инт. масштаб турбулентности
L(t) =
R
∞
0
B
LL
(r, t)dr
B
LL
(0, t)
=
48
√
2π(νt)
5/2
Λ
·
Λ
48
√
2π(νt)
5/2
Z
∞
0
e
−
r
2
8νt
dr =
=
Z
∞
0
e
−
r
2
8νt
dr =
1
2
p
π · 8νt =
√
2πνt,
т.е. мелкие вихри вырождаются, а крупные оста-
ются.
4.3 Найти выражение для корреляционной
функции пульсаций температуры в инерционном и
вязком интервале R
T T
=< δT
02
>, используя тео-
рию локально изотропной турбулентности Колмо-
горова.

5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 60
Решение
В турбулентном потоке при наличии пульса-
ций скорости и температуры имеются следующие
размерные величины:
ε
T
= a
¿
³
∂T
0
∂r
n
´
2
À
, [ε
T
] =
δ T
2
τ
- поток по спектру пульсационной
тепловой энергии
ε =
ν
2
¿
³
∂u
i
∂x
r
+
∂u
k
∂x
i
´
2
À
, [ε] =
l
2
τ
3
- поток кинетической
пульсационной энергии
ν, P r =
a
ν
; [ν] = [a] =
l
2
τ
3
- коэффициенты вязкости и
температуропроводности
R
T T
=< (δT
0
)
2
>=< [T
0
(r)−T
0
(0)]
2
>=< T
02
(r) > −2 < T
0
(r)T
0
(0) > + < T
02
(0) >;
R
T T
= 2[< T
02
(0) > − < T
0
(r)T
0
(0) >] (1),
т.к. турбулентность изотропна < T
02
(r) >=<
T
02
(0) >. Из теории размерностей следует
R
T T
= ε
T
³
ν
ε
´
1/2
f
µ
r
r
0
, P r
¶
, r
0
=
µ
ν
3
ε
¶
1/4
В инерционном интервале не должно быть зависи-
мости от ν, поэтому
R
T T
=< δT
02
>= const · P r
k
ε
T
ε
−1/3
r
2/3
[R
T T
] =
(δT )
2
τ
·
µ
l
2
τ
3
¶
−1/3
r
2/3
= (δT )
2
³
r
l
´
2/3
.
В инерционном интервале можно использовать
связь между R
T T
и ε
T
:
ε
T
= a
¿
∂T
0
∂r
n
∂T
0
∂r
k
À
= a
·
∂
∂r
n
¿
T
0
∂T
0
∂r
k
À
−
¿
T
0
∂
2
T
0
∂r
n
∂r
k
À¸
=
=
a
2
∂
2
∂r
2
k
< T
02
> −a
¿
T
0
∂
2
T
0
∂r
2
k
À
= −a
¿
T
0
∂
2
T
0
∂r
2
k
À
Из формулы (1) следует:
∂
2
R
T T
∂r
2
k
= −2
¿
T
0
(0)
∂
2
T
0
(r)
∂r
2
k
À
;
∂
2
R
T T
∂r
2
k
(0) = −2
¿
T
0
(0)
∂
2
T
0
∂r
2
k
¯
¯
¯
¯
0
À
=
2ε
T
a
(2)
В вязком интервале T
0
(r) = T
0
(0)+r
∂T
∂r
(0), поэтому
R
T T
=< (δT
0
)
2
>= r
2
·
∂T
∂r
(0)
¸
2
= Ar
2
Подставляя в (2), получим
2ε
T
a
= 2A
∂
∂r
k
³
r −
r
k
r
´
= 2A
∂r
k
∂
k
= 2A · 3 = 6A
A =
ε
T
3a
, R
T T
=
ε
T
3a
r
2
.
Ответ:
R
T T
=
½
constP R
k
ε
T
ε
−1/3
r
2/3
, r > r
0
ε
T
3a
r
2
, r < r
0
4.4. Используя теорию Прандтля, найти закон
сопротивления для плоского канала, считая напря-
жение трения постоянным по сечению канала.
Решение
1)Напряжение трения в пограничном слое
(1)
τ = ρν
∂u
∂y
= const (η < η
∗
- ламинарный подслой)
τ = ρl
2
³
∂u
∂y
´
2
(η > η
∗
- турб. область)
Определим динамическую скорость τ = ρu
2
∗
и без-
размерную скорость U = u/u
∗
. В канале можно
ввести две безразмерные координаты
ξ =
µ
1 −
y
α/2
¶
η =
(α/2 − y)u
∗
ν
(2)
Между которыми имеется соотношение
η
ξ
=
du
∗
ν
=
d¯u
2ν
·
u
∗
¯u
=
Re
¯
U
(3)
где ¯u =
1
bd
R
d/2
−d/2
u(y)bdy =
R
1
0
u(ξ)dξ. Или в безраз-
мерном виде
¯
U =
¯u
u
∗
=
Z
1
0
U(ξ)dξ (4)
Из (1) и формулы Прандтля l = κy; κ = 0, 4 - по-
стоянная Прандтля, следует распределение скоро-
стей:
¯
U =
½
η, при - η < η
∗
ламинарный подслой
1
κ
lnη, при η > η
∗
- турб. область
(5)
Найдем среднюю скорость по формуле (1), исполь-
зуя распределение скоростей (5). При этом ла-
минарным подслоем можно пренебречь, т.к. хотя
U → −∞ eta → 0, интеграл (5) сходится:

5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 61
¯
U =
Z
1
0
1
κ
lnydξ =
¯
U
κRe
Z
Re/
¯
U
0
ln ydy
Z
a
0
lnxdx =
Z
a
0
x
0
lnxdx = xlnx|0
a
−
Z
a
0
x·
1
x
dx = A(lnA−1)
¯
U =
¯
U
κRe
·
Re
¯
U
µ
ln
Re
¯
U
− 1
¶
=
1
κ
ln
Re
¯
U
−
1
κ
(6)
2) Коэффициент сопротивления определяется из
условия баланса сил:
τ(0) · S = ∆p · S; ∆p = λ
ρ¯u
2
2
L
d
Подставляя напряжение трения τ = τ(0) = ρu
2
∗
:
ρu
2
∗
bL = λ
ρ¯u
2
2
L
d
· bd
Отсюда получаем связь между коэффициентом со-
противления и средней скоростью:
λ = 2
³
u
∗
¯u
´
2
=
2
¯
U
2
;
¯
U =
r
2
λ
Подставим в (6):
λ
−1/2
=
1
κ
√
2
ln
Re
√
λ
√
2
−
1
κ
=
1
κ
√
2
ln(Re
√
λ)−
1
2κ
√
2
ln2−
1
κ
или
λ
−1/2
= 4, 08 lg(Re
√
λ) − 3, 11
сравни с сопротивлением для круглой трубы:
λ
−1/2
= 2, 035 lg(Re
√
λ) − 3, 11
4.5. Найти асимптотический (при t → ∞)
закон изменения кинетической энергии продоль-
ных пульсаций скорости и продольного масштаба
однородного турбулентного движения проводящей
жидкости в магнитном поле при малых значениях
магнитного числа Рейнольдса на стадии вырожде-
ния турбулентности.
Решение
Уравнение типа Кармана-Ховарта для одно-
родной МГД-турбулентности имеет вид (см. лек-
ции или учебное пособие)
∂Φ
ij
∂t
= A
ij
(
~
k) + B
ij
(
~
k) − 2νk
2
Φ
ij
− γ
r
cos
2
ϕΦ
ij
(1)
Где γ
r
= 2C
2
a
/ν
m
, ϕ =
d
k · W На стадии вырожде-
ния турбулентности (∆
ij
= B
ij
= 0) уравнение (1)
имеет решение
Φ
ij
(k, t) = Φ
(o)
ij
(k) exp[−(γ
r
cos
2
φ + 2νk
2
)t] (2)
Если в каждый момент турбулентность была изо-
тропной,
Φ
(o)
ij
(k) =
2π
2
E(k)
k
2
µ
δ
ij
−
k
i
k
j
k
2
¶
; Φ
(o)
ii
=
4π
2
E(k)
k
2
(3)
t = 0 : < v
i
v
i
>= 2π
2
R
∞
0
E(k)
k
2
· 2
4πk
2
dk
(2π )
3
=
2
R
∞
0
E(k)dk 1) Найдем закон изменения кинети-
ческой энергии продольных пульсаций:
ξ
11
=
< u
02
>
2
=
1
2
Z
Φ
11
(kt)
d
3
k
(2π)
3
=
1
2 · (2π)
3
Z
∞
0
2π
2
E(k)
k
2
2πk
2
dk·
·
Z
π
0
(1 − cos
2
ϕ)sinϕdϕ · e
−(γ
n
cos
2
ϕ)t−2ϑk
2
t
=
=
1
2
Z
∞
0
E(k)e
−2ϑk
2
t
dk
Z
1
0
(1 − µ
2
)e
−γ
n
µ
2
t
dµ
При t → ∞
R
∞
0
E(k)e
−2ϑk
2
t
=
3
2
W
2
0
(t) убывание без
учета магнитного поля
(при Re À 1, ϑk
2
t ¿ 1 W
0
сохраняется)
Z
1
0
(1 − µ
2
)e
−2ϑk
2
t
dµ =
=
1
√
γ
n
t
Z
√
γ
n
t
0
(1 −
x
2
γ
n
t
)e
−x
2
dx
−→
t → ∞
√
π
2
√
γ
n
t
W
2
11
W
2
0
=
3
2
·
√
π
2
√
γ
n
t
=
3
4
r
π
γ
n
t
2) Найдем закон изменения продольного масштаба
турбулентности
l
11
=
R
∞
−∞
< v
i
˜v >
r
2
,r
3
=0
dr
1
< v
i
˜v >
=
R
Φ
ii
(0, k
2
, k
3
)
dk
2
dk
3
(2π )
2
R
Φ
ii
(k)
d
3
k
(2π )
3
, ..
5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 62
Z
∞
−∞
< v
i
˜v >
r
2
,r
3
=0
dr
1
=
Z
∞
−∞
µ
Z
Φ
ii
(k, r)r
ik
1
r
1
d
3
k
(2π)
3
¶
dr
1
=
=
Z Z
Φ
ii
(0, k
2
, k
3
)
dk
2
dk
3
(2π)
2
.
Здесь Φ
ii
определяется из (3)
Φ
ii
(0, k
2
, k
3
) =
2π
2
E(k)
k
2
(3 − 1) =
4π
2
E(k)
k
2
ll
11
=
R
∞
0
E(k)
k
2
2πkdk
R
∞
0
4π
2
E(k)
k
2
·
4πk
2
dk
(2π)
3
= π ·
R
∞
0
E(k)
k
dk
R
∞
0
E(k)dk
В маг-
нитном поле с учетом ϕ = π/2 (только для
интеграла в числителе) получаем
l
11
(t) = π
R
∞
0
E(k)e
−2ϑk
2
t
k
dk
R
∞
0
R
1
−1
E(k)e
−2ϑk
2
t−γ
n
µ
2
t
dkdµ
При t → ∞
l
11
(t) → π
R
∞
0
k
3
e
−2νk
2
t
dk
R
∞
0
k
4
e
−2νk
2
t
dk · 2
R
1
0
e
−γ
n
µ
2
t
dµ
2
Z
1
0
e
−γ
n
µ
2
t
dµ =
2
√
γ
n
t
Z
√
γ
n
t
0
e
−x
2
dx =
2
√
γ
n
t
·
√
π
2
=
r
π
γ
n
t
т.к. при t → ∞ основной вклад в интеграл дает
область малых k, где E(k) = ck
4
.
l
11
(t) = π
√
2ϑt
I
3
I
4
,
где
I
3
=
Z
∞
0
x
3
e
−x
2
dx =
1
2
(2) =
1
2
I
4
=
Z
∞
0
x
4
e
−x
2
dx =
1
2
Γ
µ
5
2
¶
=
1
2
·
3
2
·
1
2
√
π =
3
√
π
8
¯
l
11
=
¯
l
(o)
11
¯
l
n
11
l
11
k '
4
3
√
2πϑt ;
¯
l
n
11
=
r
γ
n
t
π
;
¯
l
11
∼ t
Увеличение продольного масштаба связано с влия-
нием магнитного поля и вырождением турбулент-
ности (затуханием мелких масштабов).
4.6. Показать, что для однородной изотроп-
ной турбулентности в несжимаемой среде двух-
точечный момент скоростей третьего порядка <
v
i
(x)v
j
(x)v
l
(x+r) > определяется только продоль-
ной корреляционной функцией < v
2
L
(0)v
L
(r) >, v
L
- проекция вектора скорости на направление r, со-
единяющее рассматриваемые точки.
Решение
Двухточечный момент второго порядка
B
ij,l
(x, r) =< v
i
(x)v
j
(x)v
l
(x + r) >
для однородной изотропной турбулентности имеет
вид
B
ij,l
(0, r) =< v
i
(0)v
j
(0)v
l
(r) >== B
1
(r)
r
i
r
j
r
l
r
3
+B
2
(r)
(δ
jl
r
j
+ δ
il
r
j)
r
+B
3
(r)δ
ij
r
l
r
(1)
Выразим функции B
1
, B
2
, B
3
через три следу-
ющих момента:
B
LL,L
(r) =< v
2
L
(0)v
L
(r) >,
B
NN,L
(r) =< v
2
n
(0)v
L
(r) >,
B
LN,N
(r) =< v
L
(0)v
n
(0)v
n
(r) >
В результате получаем:
B
ij,l
(r) = (B
LL,L
−B
NN,L
−2B
LN,N
)
r
i
r
j
r
l
r
3
+B
LN,N
δ
jl
r
i
+ δ
il
r
j
r
+B
NN,L
δ
ij
r
l
r
Используем уравнение неразрывности
∂B
ij,l
∂r
l
= 0,
тогда получим
B
NN,L
= −
1
2
B
LL,L
; B
LN,N
=
1
2
µ
1 +
r
2
d
dr
¶
B
LL,L
т.е. все 27 компонент тензора B
ij,l
выражены через
B
LL,L
B
i,jl
(r) = B
il,i
(r)
При проверке задать вопросы: написать
B
12,1
..
4.7. Найти асимптотическую зависимость от
времени при t → ∞ масштаба турбулентных пуль-
саций температуры для однородной изотропной
турбулентности на стадии распада турбулентного
движения.
Решение
Уравнение для пульсаций температуры, ана-
логичное уравнению Кармана-Ховарта, имеет вид:
∂B(r, t)
∂t
=
1
r
2
∂
∂r
r
2
µ
B
LT,T
+ cosh i
∂B(r, t)
∂r
¶
,

5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 63
B =< T
0
(0)T
0
(r) >
cosh i - температуропроводность. На стадии
распада турбулентности, когда B
LT,T
=<
v
L
(0)T
0
(0)T
0
(r) >= 0 получаем уравнение:
∂B(r, t)
∂t
= cosh i
1
r
2
∂
∂r
r
2
∂B(r, t)
∂r
,
которое является решением теплопроводности в
трехмерном пространстве и имеет решение:
B(r, t) =
1
(8π cosh it)
3/2
Z
B(r
0
, 0) exp
·
−
(r − r
02
)
8 cosh it
¸
d
3
r
0
Интегрируя по угловым переменным в сфериче-
ской системе координат, получаем
B(r, t) =
1
r
√
2π cosh it
Z
B(r
0
, 0) sinh
µ
rr
0
4 cosh it
¶
exp
µ
−
r
2
− R
02
8 cosh it
¶
r
0
dr
0
В пределе при t → ∞ находим асимптотическое
выражение
B(r, t) '
k
4
√
2π(cosh it)
3/2
exp
µ
−
r
2
8 cosh it
¶
,
где K =
R
∞
0
r
2
B(r, t)dt - инвариант Корсина. Из-
менение интегрального масштаба турбулентности:
L =
1
B(0, t)
Z
∞
0
B
LL
(r, t)dr =
Z
∞
0
e
−
r
2
8 cosh it
dr =
1
2
√
8π cosh it =
√
2π cosh it
Масштаб растет вследствие вырождения мелко-
масштабного движения.
4.8. Найти выражение для двухточечного мо-
мента < T
0
(v
0
)
2
> в инерционном интервале, ис-
пользуя теорию локально-изотропной турбулент-
ности Колмогорова.
Решение
В турбулентном потоке без пульсаций темпе-
ратуры определяющими величинами являются по-
ток кинетической пульсационной энергии по спек-
тру ε = ϑ <
³
∂v
0
i
∂xk
´
2
> и вязкость ϑ, имеющих
размерности [ε] = l
2
/τ
3
, [ϑ] = l
2
/τ. В потоке с
пульсацией температуры появляются поток пуль-
сационной тепловой энергии ε
T
= a <
³
∂T
0
∂xk
´
2
> и
коэффициент температуропроводности a, размер-
ности которых
[ε
T
] =
∆T
2
τ
, [a] = [ϑ] =
l
2
τ
Итого, имеются следующие параметры:
ε, ε
T
, ϑ, P
r
=
a
ϑ
Используем теорию размер-
ностей для нахождения двухточечного момента
третьего порядка:
< ∆T
0
(∆v
02
) >= ε
1/2
T
ϑ
1/2
f
µ
r
r
0
, P r
¶
?
где r
0
=
³
ϑeta
3
ε
´
1/4
, т.к. [ε
T
ϑ]
1/2
=
³
∆T
2
τ
·
l
2
τ
´
1/2
=
∆T ·
l
τ
. В инерционном интервале не долж-
но быть зависимости от вязкости, поэтому
< ∆T
0
(∆v
02
) >= ConstP
k
r
ε
1/2
T
ε
1/6
r
2/3
- ответ. ?
< ∆T
0
(∆v
0
)
2
>= Constε
1/2
T
ε
1/2
r
4.9. Найти закон турбулентного теплообмена
St = f(P r, P e) в цилиндрической трубе исполь-
зуя теорию Прандтля и считая турбулентное число
Прандтля P r
T
= 1. (число Струхаля определяется
отношением теплового потока на стенку к средне-
му конвективному потоку
St =
q
w
ρC
p
< u∆T >
, ∆ = T − T
w
,
угловыми скобками обозначено среднее значение
по сечению трубы).
Решение
Среднее значение величины A(r) по сечению
трубы определяется по формуле
< A >=
1
πR
2
Z
R
0
A(r)2πrdr = 2
Z
a
0
A(ξ)ξdξ (1)
По определению числа Струхаля
St
−1
=
ρc
p
< u∆T >
q
w
(2)
Распределение скоростей в трубе при турбулент-
ном движении является логарифмическим: u =
u
∗
κ
ln η, где η =
(R−r)u
∗
ϑ
. Связь между координа-
тами η и ξ:
η =
Ru
∗
ϑ
³
1 −
r
R
´
=
R¯u
ϑ
·
u
∗
¯u
³
1 −
r
R
´
=
Re
¯
U
(1−ξ); ξ = 1−
¯
U
Re
η
Здесь U =
u
u
∗
;
¯
U =
¯u
u
∗
. Найдем распределение тем-
ператур в турбулентном пограничном слое. Опре-
деляется из выражения для теплового потока, ко-
торый будем считать постоянным в слое:
q
w
= −q = ρc
p
a
T
dT
dy
Примем турбулентное число Прандтля P R
T
= 1,
т.е. a
T
= ϑ
T
= lu
∗
= κy · u
∗
(κ = 0.4 - постоянная
Прандтля)
q
w
ρc
p
κu
∗
= y
dT
dy
= η
dT
dy
5 ЗАДАНИЕ 4. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД) 64
отсюда находим распределение температур в слое:
T − T
w
= ∆T (η) =
q
w
ρc
p
κu
∗
ln η
Подставляя в (2) и учитывая распределение ско-
ростей и температур, получим
St
−1
=
ρc
p
< u∆T >
q
w
=
ρc
p
q
w
·
u
∗
κ
·
q
w
ρc
p
κu
∗
< ln
2
η >=
1
κ
2
< ln
2
η >
Найдем среднее значение < ln
2
η >:
< ln
2
η >= 2
Z
1
0
ln
2
ηξdξ = 2
Z
Re
U
0
ln
2
η
µ
1 −
¯
U
Re
η
¶
¯
U
Re
dη =
=
2
A
Z
a
0
³
1 −
η
A
´
ln
2
ηdη =
2
A
J
1
−
2
A
2
J
2
,
где A =
Re
¯u
= Re
q
λ
8
. Здесь использована связь
средней скорости ¯u с коэффициентом сопротивле-
ния
¯
U
2
=
8
λ
.
J
1
=
Z
a
0
ln
2
ηdη =
Z
a
0
η
0
ln
2
ηdη = η ln
2
η
¯
¯
0
a
−
Z
a
0
η·2lnη·
1
η
dη = A ln
2
A−2A ln A+2A.
J
2
=
Z
a
0
ln
2
ηdη =
Z
a
0
µ
η
2
2
¶
0
ln
2
ηdη =
η
2
2
ln
2
η
¯
¯
¯
¯
0
a
−
Z
a
0
η
2
2
·2 ln η·
1
4
dη =
A
2
2
ln
2
A−
A
2
2
ln A+
A
2
4
< ln
2
η >=
2
A
[A ln
2
A−2A ln A+2A]−
2
A
2
·
A
2
2
ln
2
A −
A
2
2
ln A +
A
2
4
¸
= ln
2
A−3 ln A+3, 5
St
−1
=
1
κ
2
[ln
2
A − 3 ln A + 3, 5]
Или, подставляя выражение для A, получим:
St
−1
=
1
κ
2
"
ln
2
Re
√
λ
√
8
− 3 ln
Re
√
λ
√
8
+ 3, 5
#
Для построения зависимости St(Re) необходимо
использовать выражение для коэффициента со-
противления:
r
8
λ
=
1
κ
"
ln
Re
√
λ
2
√
8
+ κ −
3
2
#
Построим график этой зависимости:
4.10. Найти асимптотический (при t → ∞)
закон изменения кинетической энергии попереч-
ных пульсаций скорости и поперечного масштаба
однородного турбулентного движения проводящей
жидкости в магнитном поле при малых значениях
магнитного числа Рейнольдса на стадии вырожде-
ния турбулентности.
Решение
См.задачу 1.5.
Φ
ij
(k, t) = Φ
(o)
ij
(k) exp[−(γ
r
cos
2
ϕ + 2ϑk
2
)t]
Φ
(o)
ij
(
¯
k) =
2π
2
E(k)
k
2
µ
δ
ij
−
k
i
k
j
k
2
¶
, Φ
(o)
ii
=
4π
2
E(k)
k
2
1) Найдем закон изменения кинетической энергии
поперечных пульсаций:
w
2
⊥
=
Z
Φ
22
(k, t)
d
3
k
(2π)
3
=
Z
∞
0
2π
2
E(k)
k
2
e
−2ϑk
2
t−γ
r
cos
2
ϕt
·k
2
dk
Z
π
ϕ=0
Z
2π
ϑ=0
(1−sin
2
ϕcos
2
ϑ)·
·sinϕdϕdϑ =
1
4π
Z
∞
0
E(k)e
−2ϑk
2
t
dk
µ
2π − sin
2
ϕ
Z
2π
0
1 + cos
2
ϑ
2
dϑ
¶
·e
−γ
r
cos
2
ϕt
,
(2π − sin
2
ϕπ) = π(2 − sin
2
ϕ) = π(1 + cos
2
ϕ)
w
2
⊥
=
1
4
Z
∞
0
E(k)e
−2ϑk
2
t
dk · 2
Z
1
0
(1 + µ
2
)e
−γ
r
µ
2
t
dµ
На асимптотически больших временах
3w0
2
2
≡
Z
∞
0
E(k)e
−2ϑk
2
t
dk À
Z
∞
0
Λ
3π
k
4
e
−2ϑk
2
t
dk =
Λ
32
√
2π(ϑt)
5/2
Z
1
0
(1+µ
2
)e
−γ
r
µ
2
t
dµ =
1
√
γ
r
t
Z
√
γ
r
t
0
µ
1 +
x
2
γ
r
t
¶
e
−x
2
dx =
1
√
γ
r
t
√
π
2
w
2
⊥
w
2
0
=
3
8
·
√
π
γ
r
t
в 2 раза меньше, чем
w
2
||
w
2
0
.
2) Найдем значение изменения поперечного
масштаба турбулентности
l
⊥
=
R
∞
−∞
< v
i
˜v
i
>
r
1
,r
3
=0
dr
2
< v
i
˜v
i
>
=
R
Φ
ii
(k
1
, 0, k
2
)
dk
1
dk
2
(2π )
2
R
Φ
ii
(k)
d
3
k
(2π )
2
Φ
ii
(k
1
, 0, k
2
) =
2π
2
E(k)
k
2
(3 − 1) =
4π
2
E(k)
k
2
l
⊥
= π
R
∞
0
(E(k)/k)e
−2ϑk
2
t
dk · 2
R
1
0
e
−γ
r
µ
2
t
dµ
R
∞
0
E(k)e
−2ϑk
2
t
dk
= l
||
·
2
√
γ
r
t
√
π
2
l
⊥
=
4
3
√
2πϑt ·
r
π
γ
r
t
=
4
3
π
s
2ϑ
γ
r
= const
6 ЛИТЕРАТУРА 65
6 Литература
1. Сон Э.Е. Лекции по физической механике, 2001,
2005, 2010.
2. А.В. Леванов, Э.Е. Антипенко Определе-
ние термодинамических свойств статистическими
методами. Классический идеальный газ М., МГУ,
Химический факультет, 2006, 44с.
