Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

6.7. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ТИПЫ ТУРБУЛЕНТНОСТИ 231

Постоянные a, b, c можно определять из решения задачи при g = 0, используя опытные

данные для величин:

< (u

)

< (v

)

≈ 1, 7(погр.слой); 1.53(трубы)

< (w

)

< (v

)

≈ 1, 4(погр.слой); 1.21(трубы)

Φ =

< u

∗

≈ 6, 8(погр.слой); 7, 15(трубы)

R =

< u

< (u

)

>< (v

)

= 0 .19

В результате находим следующие значения постоянных:

a ≈ 0.14, b ≈ 0.08, c ≈ 0.03.

Дальнейшее рассмотрение можно провести аналогично (6.237) - (6.242), при этом полу-

чаются утонченные, но качественно согласующиеся результаты.

6.7.2 Турбулентное течение жидкости с полимерными добавками

В 1949 году Томсом [68] экспериментально был открыт эффект снижения сопротивле-

ния тел в турбулентном потоке жидкости при добавлении небольшого количества по-

лимерных молекул. Эффект Томса подробно исследовался экспериментально (см. обзор

Г.Ф.Кобеца в [69]), и мы будем ориентироваться на следующие характерные парамет-

ры: при добавлении в раствор (0.05-0.4)% полиметаакриловой кислоты (относительная

молекулярная масса М = 1.210

) или (0.01-0.1)% полиакриловой кислоты (M = 2.410

)

происходит снижение сопротивления на (10-50)%, причем имеется зависимость сниже-

ния сопротивления от размеров полимерных макромолекул (радиус инерции молекул

изменяется от 200 до 400 А). При повышении концентрации молекул выше 0.5% насту-

пает насыщение, сопротивление далее не уменьшается. Полимерные молекулы являют-

ся спиралевидными с характерным размером `

' 4 · 10

−6

cm и в растворе "набухают".

В литературе существует два варианта объяснения эффекта Томса, рассматривающие

влияние полимерных добавок на вязкость жидкости (см. в [69]) и их влияние на гид-

родинамическое движение полимерных молекул в среде [70], [71]. Мы рассмотрим гид-

родинамическое влияние полимерных молекул на турбулентное движение жидкости, но

отличное от описанных в литературе [70], [71]. Примем массовую концентрацию поли-

мерных молекул C

= n

/ρ = 10

−3

, откуда найдем их молярную концентрацию

ρc

1 · 10

−3

· 1.6 · 10

−24

= 6 · 10

−3

Будем считать, что при смещении среды относительно полимерной молекулы, послед-

няя "скрепляет"жидкостной наполнитель в объеме (4/3)π`

, который образует присо-

единенную массу по величине превышающую массу полимерной молекулы:

π`

≈ 160.

232 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Рассмотрим движение жидкой частицы, содержащей полимерную молекулу и испыты-

вающую вязкое трение в жидкости. Силу трения можно оценить следующим образом:

напряжение трения равно

τ = µ

∂v

∂r

µv

отн

где µ - вязкость жидкости, v

отн

- относительная скорость движения частицы и среды,

- характерный размер жидкой частицы. Сила трения приближенно равна F = τ S =

µv

отн

; если бы частица была твердым шаром радиуса `

, то C = 6π по закону со-

противления Стокса, но для жидкой несферичной частицы мы далее для оценок примем

С=10. Уравнение движения частицы имеет вид:

= −C`

µ(v

− v) (6.264)

или

= −(v

− v), (6.265)

где M = m

+ m

≈ m

, а время релаксации импульса

m + m

≈

4π`

3C`

ρν

≈ 0.4

≈ 6.4 · 10

−10

cek,

Сравним эту величину с частотой турбулентных пульсаций в пограничном слое в близи

т.н. "ламинарного подслоя", т.к. полимерные добавки оказывают наибольшее влияние

по-видимому, вблизи ламинарного подслоя, где частота турбулентных пульсаций выше.

Граница ламинарного подслоя δ

в соответствии с многочисленными экспериментальны-

ми данными определяется из следующего условия:

∗

/ν = 11.5,

где v

∗

τ/ρ. Полагая напряжение трения в области ламинарного подслоя равным τ ≈

ρνu

/δ

, u

≈ 0.4¯u (¯u - осредненная скорость течения), получим δ

≈ 325ν/¯u. Положим

масштаб турбулентных пульсаций ` = 0.4δ

= 130 ν/¯u, а характерную скорость u ≈

0.05¯u, ¯u = 10

cm/cek, тогда частота турбулентных пульсаций ω = u/` ≈ 6 · 10

cek

−1

, ` =

−3

cm. Оценим отношение времен турбулентных пульсаций и релаксации импульса

полимерной молекулы:

= ωτ

= 4 · 10

−5

¿ 1.

Малая величина параметра ωτ

указывает, что полимерная молекула увлекается жид-

кой средой и, следовательно, почти не вызывает сопротивления движению, но при пуль-

сационном турбулентном движении часть кинетической энергии жидкости затрачива-

ется на работу против сил трения, следовательно, имеется дополнительная к вязкой

диссипация кинетической энергии турбулентности. Следует ожидать, что если этот ме-

ханизм диссипации будет сравним с вязкой диссипацией, то влияние полимерных доба-

вок будет существенно для снижения сопротивления тел, движущихся в турбулентном

потоке. Найдем диссипацию, связанную с полимерными молекулами. Будем считать, что

жидкость совершает периодическое пульсационное движение v = v

sin ωt с частотой ω.

Тогда движение жидкой частицы на временах, превышающих τ

, когда частица "забы-

вает"о начальных условиях, определяется частным решением неоднородного уравнения

6.7. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ТИПЫ ТУРБУЛЕНТНОСТИ 233

( 6.264):

1 + ω

(sin ωt − ωτ

cos ωt). (6.266)

Найдем величину диссипации кинетической энергии в единице объема за период пуль-

сации T = 2π/ω:

P = − < M

v >= cn

ell

1 + ω

< (ω

sin ωt − ωτ

cos ωt)v

cos ωt >

В результате находим величину диссипации:

P =

µv

1 + ω

. (6.267)

Параметр, определяющий отношение диссипации на полимерных молекулах к вязкой

диссипации равен

µv

(1 + ω

)(µv

)

= c

1 + ω

. (6.268)

С учетом сделанных ранее оценок,

= 10 ·

6 · 10

· 4 · 10

−6

· (10

−3

)

(4 · 10

−5

)

1 + (4 · 10

−5

)

≈ 4 · 10

−5

Отсюда следует, что рассматриваемая модель приводит к малой величине эффекта. Оце-

ним теперь параметр, определяющий отношение размера жидкой частицы с полимерной

молекулой к расстоянию между ними

≈ 0.33.

Поскольку `

∼ `

/3, а полимерные молекулы имеют вид пространственных спира-

лей ("пружин"), возможно, что при тепловом движении полимерные молекулы "зацеп-

ляются", образуя комплексы. Пусть N - среднее число молекул в таких комплексах,

концентрация которых n

= n

/N, а их характерные линейные размеры `

≈ N`

. От-

носительная величина диссипации на таких полимерных комплексах будет определяться

параметром ξ

∝ N

. Для того, чтобы эффект Томса был значительным, положим

= 0 .4, тогда среднее число полимерных молекул в комплексе должно составлять

N ' (ξ

/ξ

)

1/4

' 10 ,

что вполне может быть при `

= 1 /3. Кроме того, величина N, видимо, резко возрас-

тает с ростом концентрации молекул. Отметим, что при этом линейный размер комплек-

са `

' N`

' 4 · 10

−5

cm остается гораздо меньше масштаба турбулентных пульсаций.

Для построения полуэмпирической теории турбулентности с учетом влияния полимер-

ных молекул, примем выражение для объемной силы, действующей на жидкость

= cνn

− u

), (6.269)

а для диссипации энергии выражение ( 6.267). В результате использования приближения

"локального равновесия"получим приближенно

T 0

= (1 − ξ

)

1/2

, (6.270)

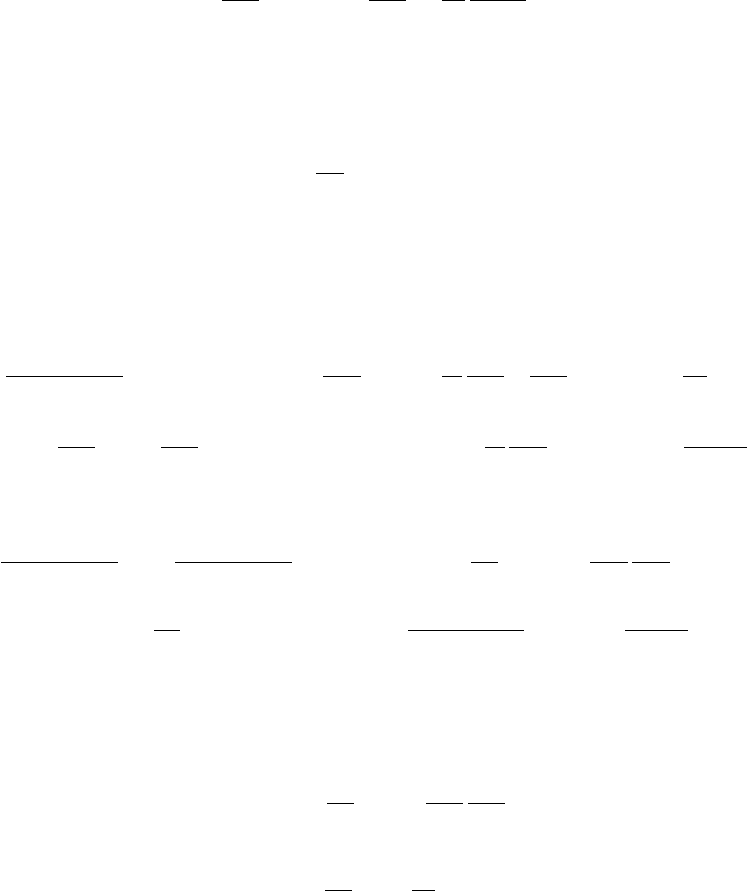
234 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

где ξ

= N

, а ξ

определяется по ( 6.268). В рассмотренной модели находят объяс-

нение как эффект снижения сопротивления полимерными добавками, так и насыще-

ние снижения сопротивления при увеличении концентрации полимерных молекул до

c ≥ 0.5%.

6.7.3 Взаимодействие турбулентного движения с тепловым излучением

В высокотемпературном газе становится существенным перенос тепла излучением, по-

этому одной из новых задач в теории турбулентности является описание взаимодействия

турбулентности с излучением. С одной стороны, излучение влияет на турбулентный пе-

ренос тепла, с другой - турбулентность влияет на перенос излучения. В разделе 6.5 рас-

сматривалось уравнение энергии в применении к турбулентному пограничному слою,

которое имеет следующий вид:

ρu

∂h

∂x

+ < ρv >

∂h

∂y

∂r

∂y

, (6.271)

где α = 0; 1 для плоского и осессиметричного течения, а поток тепла является суммой

молекулярного турбулентного и радиационного переноса тепла:

= q + uτ + q

q = −ρ

∂h

∂y

+ < v

. (6.272)

Для определения турбулентного переноса тепла (т.е. определения корреляции < v

используется уравнение вторых моментов для величины < (h

)

>, которое получает-

ся стандартным методом осреднения уравнения энергии, вычитания из неосредненного

осредненного уравнения, умножения на 2h

и последующего осреднения:

< ρv

∂ < (h

)

∂x

= −2 < (ρv

∂h

∂x

− 2

*Ã

∂h

∂x

∂h

∂x

+ 2

∂v

∂x

∂

∂x

− < (ρv

)

> +2

∂h

∂x

− 2

∂(q

)

∂x

.(6.273)

После преобразований и упрощений, характерных для пограничного слоя, получим:

ρu

∂ < (h

)

∂x

+ ρv

∂ < (h

)

∂y

= −2ρ < v

∂h

∂y

− 2ρχ

∂h

∂x

∂h

∂x

∂

∂y

−ρ < v

)

> +ρχ

∂ < (h

)

∂y

− 2

∂(q

)

∂x

. (6.274)

Последний член в (6.274) характеризует влияние излучения на турбулентный перенос

тепла. В отсутствие излучения, учитывая только члены, описывающие генерацию и

диссипацию турбулентности, получим:

− < v

∂h

∂y

≈ χ

∂h

∂x

∂h

∂x

или

∂h

∂y

≈ h

6.7. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ТИПЫ ТУРБУЛЕНТНОСТИ 235

откуда следует

= `

∂h

∂y

где `

- "длина смешения"(h

< (h

)

>) для обмена тепловой энергией. Турбулент-

ный поток тепла определяется аналогично турбулентному напряжению Рейнольдса:

= −ρ < v

>= −ρwh

= −ρχ

∂h/∂y.

Здесь χ

= w`

- турбулентный коэффициент температуропроводности. Турбулентное

число Прандтля (раздел 6.5) определяется отношением

P r

Если "длина смешения"тепла равна "длине смешения"импульса, то P r

≈ 1. Обычно,

однако, принимается значение, более согласующееся с опытными данными P r

≈ 0.9.

Качественное влияние излучения на турбулентность сводится к тому, что при высоких

температурах увеличивается охлаждение перегретых турбулентных вихрей и нагрев бо-

лее холодных, поэтому пульсации температуры сглаживаются. В низкотемпературных

областях возможно увеличение пульсаций температуры под действием потока излучения

из областей высоких температур. Для определения количественного влияния излучения

на турбулентный перенос тепла рассмотрим два предельных случая, соответствующих

оптически толстым и оптически тонким вихрям. Для оптически толстых вихрей, когда

` >> 1 (κ

- коэффициент поглощения, ` - размер крупных энергонесущих вихрей),

лучистый поток тепла по форме совпадает с молекулярным, но с коэффициентом лучи-

стой теплопроводности:

= −λ

∇T = −(λ

)∇h.

Общий поток тепла

q = ρ(χ + χ

+ χ

)

∂h

∂y

может рассматриваться как сумма молекулярного, куда входит радиационный перенос,

и турбулентного. При высоких температурах радиационный перенос тепла возрастает и

может сравниться с турбулентным. Для оптически тонких турбулентных вихрей κ

` ¿

1. Этот случай чаще встречается в практических приложениях. Из теории переноса

излучения следует, что в этом случае определяется дивергенция радиационного потока

излучения через средний планковский коэффициент поглощения κ

div~q

dν = 4πκ

B(T ).

Здесь do - элемент телесного угла, B(T ) - функция Планка для интенсивности излучения

черного тела. Преобразуем в уравнении (6.274) член, учитывающий влияние излучения

на турбулентность:

< h

∇ ·

>=< ( h

)

4π

∂(κ

∂T

т.к. коэффициент поглощения и интенсивность излучения черного тела являются функ-

циями температуры:

(κ

∂(κ

∂T

, T

236 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Рис. 6.7: Влияние излучения на турбулентный перенос тепла. P r

(

R) - турбулентное число Прандтля с

учетом излучения, P r

- без учета. Расчет выполнен для пограничного слоя толщиной δ, при темпе-

ратуре стенки T

= 1600K, температуре на внешней части пограничного слоя

T = 5500K, для смеси

+ 1.5%(N a + K) при р=50 атм.

Учитывая этот член в уравнении баланса генерации и диссипации, получим

∂h

∂y

= h

+ h

4π

∂(κ

∂T

отсюда находим

1 + f

∂h

∂y

, (6.275)

где f

- коэффициент, учитывающий влияние излучения на турбулентный перенос теп-

ла:

4π`

∂(χ

∂T

Коэффициент турбулентной температуропроводности и турбулентное число Прандтля

в данном случае равны

< v

∂h/∂y

1 + f

P r

(R)

P r

1 + f

Из расчетов следует, что излучение примерно в пять раз уменьшает турбулентное число

Прандтля. Рассмотрим обратное влияние турбулентности на перенос излучения. Уравне-

ние переноса излучения входит в систему уравнений, описывающих гидродинамическое

движение среды. Как и все остальные уравнения в турбулентном течении, оно должно

быть осреднено:

∂ < I

∂s

=< κ

> − < χ

> . (6.276)

Осреднение величин в правой части этого уравнения можно провести в двух предель-

ных случаях, соответствующих оптически тонким и оптически толстым турбулентным

6.7. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ТИПЫ ТУРБУЛЕНТНОСТИ 237

вихрям. Рассмотрим случай κ

` ¿ 1, что соответствует оптически тонким вихрям. В

этом случае

< κ

>= κ

∂

(κ

)

∂T

< (T

)

> .

Член, содержащий первую производную, сокращается при осреднении. При рассмотре-

нии задач с турбулентным переносом тепла пульсациями < (T

)

> пренебрегалось, а

при переносе излучения в турбулентной среде их нужно учитывать из-за сильной зави-

симости излучения черного тела B

от температуры. Осреднение другого члена в (6.276)

производится следующим образом:

< κ

>=< κ

>< I

> + < κ

> .

Коэффициент поглощения не так резко зависит от температуры, поэтому < κ

(T ) >≈

(< T >). Член < κ

> определяется распределением температуры на длине κ

−1

`, на которой турбулентные пульсации усредняются, поэтому < κ

>≈ 0. В результа-

те для случая оптически тонких турбулентных вихрей получаем следующее уравнение

переноса излучения:

∂I

∂s

= κ

∂

∂T

< (T

)

> −κ

. (6.277)

Здесь

=< I

>, κ

= κ

(< T >), B

=< B

> .

В другом предельном случае, когда турбулентные вихри являются оптически толстыми

(κ

` >> 1), излучение близко к черному с интенсивностью

< B

>≈ B

∂

∂T

< (T

)

а коэффициент поглощения κ

≈ κ

(< T >), поэтому уравнение переноса излучения

имеет вид:

∂I

∂s

= κ

(< B

> − < I

>) ≈ κ

∂

∂T

< (T

)

> −κ

. (6.278)

При совместном решении уравнения переноса излучения и уравнения энергии в энталь-

пийной форме < (T

)

>=< (h

)

> /c

, тогда из уравнений (6.277) и (6.278) можно

найти < I

> и < ~q

>. Обычно влияние излучения на турбулентность может изменить

турбулентное число Прандтля в несколько раз (см. рис. 6.7), а влияние турбулентности

на излучение изменяет радиационный поток тепла на 10-20%.

6.7.4 Турбулентность многокомпонентных реагирующих сред

Многокомпонентность газа приводит в первую очередь к возникновению эффектов диф-

фузии и химических реакций. При этом по сравнению с турбулентным пограничным

слоем в однокомпонентном газе изменяется уравнение баланса энергии и уравнения

диффузии. Наличие химических реакций также влияет на гидродинамику течения. При

этом возможны два предельных случая - "замороженный"и химически равновесный. В

238 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

"замороженном"случае протеканием химических реакций можно пренебречь, ограничи-

ваясь рассмотрением диффузии компонентов. В другом предельном случае "локально-

химически равновесного"течения следует перейти к "элементному"описанию, когда со-

храняется только уравнение диффузии элементов, а концентрации компонентов опре-

деляются из уравнений равновесия. В промежуточном случае, когда время протекания

реакции по порядку равно времени турбулентных пульсаций, нужно учитывать нерав-

новесность химических реакций. Запишем уравнения диффузии и энергии в многоком-

понентном турбулентном пограничном слое при наличии одной химической реакции:

∂c

∂x

+ v

∂c

∂y

∂i

∂y

ξ, (6.279)

где член

ξ описывает конечную скорость протекания химической реакции. В предельных

случаях "замороженного"и локально равновесного

ξ = 0.

∂h

∂x

+ v

∂h

∂y

∂q

∂y

(6.280)

Здесь потоки массы и тепла в стенку определяются по формулам:

i = i

мол

− ρ < v

>, i

мол

= ρD

∂c

∂y

+ κ

∂T

∂y

= q + uτ + q

, q = q

мол

− ρ < v

Молекулярный поток тепла с учетом переноса энергии при химических реакциях

мол

= −λ

∂T

∂y

Из баланса величины < (c

)

>, аналогично < (h

)

>, приравнивая генерацию и дисси-

пацию, получим

< (c

)

> = `

∂c

∂y

, < v

>= w`

∂c

∂y

Турбулентный коэффициент диффузии D

= w`

. Здесь `

- "длина смешения"для тур-

булентной диффузии. Полагая турбулентное число Шмидта

= const(≈ 1),

получим замкнутую систему уравнений турбулентного пограничного слоя. Рассмотрим

влияние эффектов неравновесности, т.е. конечной скорости протекания химических ре-

акций, колебательной и вращательной релакcаций и т.д. на турбулентное движение.

Анализ влияния основан на сопоставлении следующих характерных времен:

прол

∼ ∆x/u - время движения газа у стенки,

∼ w/` ∼ ν

- период крупномасштабных турбулентных пульсаций,

{τ

} - матрица времен релаксации реакции между i и k - компонентами,

- время тепловой релаксации,

6.7. НЕКОТОРЫЕ СПЕЦИАЛЬНЫЕ ТИПЫ ТУРБУЛЕНТНОСТИ 239

, τ

- времена колебательной и вращательной релаксации молекул.

Возможны два предельных случая, когда учет этих процессов наиболее прост. Из набо-

ра релаксационных времен выберем минимальное и максимальное времена релаксации

min

rel

и τ

max

rel

. При τ

max

rel

>> τ

состав газа может считаться замороженным при турбу-

лентных пульсациях, в частности, теплоемкость и теплопроводность газа c

= c

, λ = f

являются "замороженными". При τ

min

рел

¿ τ

состав газа является равновесным при тур-

булентных пульсациях, в этом случае c

= c

равн

, λ = λ

равн

. В промежуточных случаях

задача усложняется из-за необходимости учета соответствующих членов в гидродина-

мических уравнениях.

240 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ