Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

1.1. ТЕРМОДИНАМИЧЕСКИЕ ПОТЕНЦИАЛЫ 11

ственных переменных:

dH = T dS + V dp + µdN, dF = −SdT − pdV + µdN, dΦ = V dp − SdT + µdN.

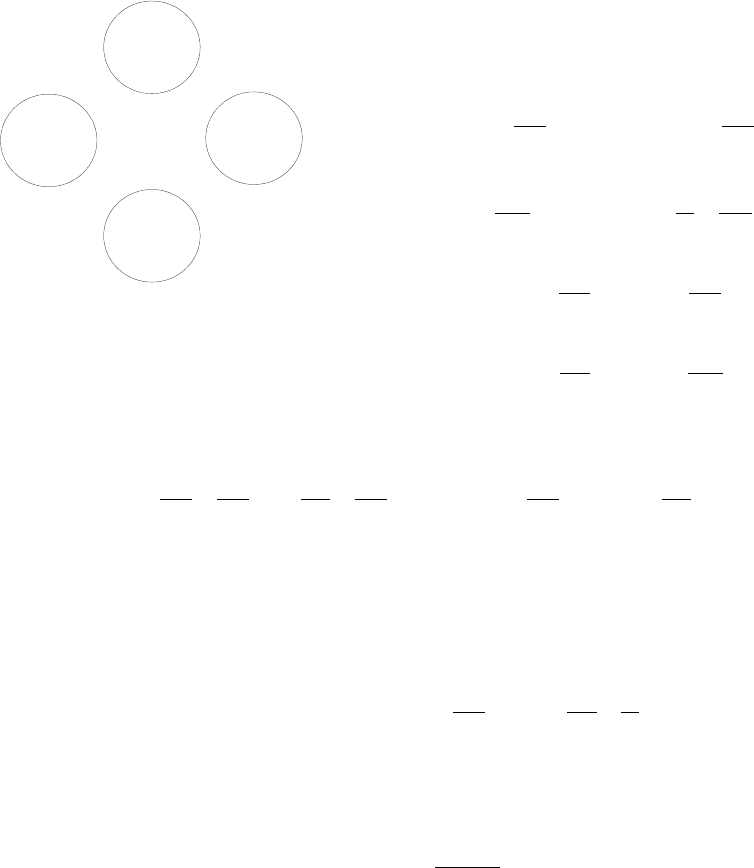
Для запоминания этих выражений можно использовать мнемоническое правило, приве-

денное на рис. 1.1.

Рис. 1.1: Термодинамические по-

тенциалы и переменные (T, p) –

интенсивные, (S, V ) – экстенсив-

ные параметры системы

Из приведенных выражений можно получить урав-

нение состояния, энтропию, химический потенциал, ко-

эффициент теплового расширения и теплоемкости си-

стемы:

p = −

∂F

∂V

T,N

, S = −

∂F

∂T

V,N

µ =

∂F

∂N

V,T

, β

∂V

∂T

T,N

= T

∂S

∂T

V,N

∂U

∂T

V,N

= T

∂S

∂T

p,N

∂H

∂T

p,N

Из выражения для дифференциала внутренней энергии можно получить соотношения

Максвелла:

∂

∂V

∂U

∂S

∂

∂S

∂U

∂V

, или

∂T

∂V

= −

∂p

∂S

Соотношение Максвелла может быть выражено через якобианы:

∂(T, S) = ∂(p, V ).

В дальнейшем нам понадобится связь между внутренней и свободной энергиями:

U = F + T S = F − T

∂F

∂T

= −T

∂

∂T

. (1.1)

В теоретической физике удобно вместо температуры использовать "обратную темпера-

туру" : β = 1/kT , где k - постоянная Больцмана. Выражение (1.1) может быть преобра-

зовано к виду

U =

∂(βF )

∂β

. (1.2)

Отметим, что, кроме термодинамических переменных S и V , термодинамические потен-

циалы также являются экстенсивными величинами.

В гидродинамике удобно использовать удельные величины, т.е. величины, приходя-

щиеся на единицу массы. В дальнейшем удельные величины будут обозначаться теми

же, но малыми буквами, что и для всей макроскопической системы. Например, u = U/M

– удельная внутренняя энергия системы, h = H/M и т.д. Иногда используются вели-

чины, приведенные на одну частицу. Например, внутренняя энергия U поделенная на

полное число частиц N, – это величина, приходящаяся на одну частицу ˜u = U/N.

12 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

1.2 Статистическая сумма

В учебном пособии некоторые формулы будут приниматься без вывода. Обычно это

формулы, которые относятся к основным теоремам, и их доказательство можно найти в

курсах теоретической физики. Так, в этом разделе в качестве основного постулата при-

нимается распределение Гиббса в каноническом ансамбле. В статистической физике его

доказательство основано на микроканоническом ансамбле (см., например, том "Ста-

тистическая физика" в курсе теоретической физики Л.Д. Ландау и Е.М. Лифшица).

Рассмотрение проведем вначале для квантовой системы, а затем перейдем к классиче-

ской системе, используя квазиклассический метод предельного перехода. Пусть система

N частиц находится в некотором квантовом состоянии n с энергией E

. Если статисти-

ческий вес этого состояния равен G

– количество состояний, имеющих одну и ту же

энергию), то в соответствии с распределением Гиббса вероятность находиться системе

в этом состоянии имеет вид

−βE

, (1.3)

где Z – нормировочная постоянная. Условие нормировки для w

следует из того, что

система находится хотя бы в одном из данных состояний, следовательно

= 1.

Cуммируя по n в формуле (1.3) и используя условие нормировки, находим выражение

для Z:

Z =

−βE

. (1.4)

Используя распределение Гиббса (1.3), найдем выражение для внутренней энергии си-

стемы. По определению внутренняя энергия системы равна сумме произведений энергий

каждого из квантовых состояний, умноженных на вероятность нахождения системы в

данном квантовом состоянии:

U =

exp(−βE

). (1.5)

Сравнивая (1.4) и (1.5), находим, что внутреннюю энергию можно выразить через про-

изводную от статистической суммы системы:

U = −

∂ ln Z

∂β

. (1.6)

Сравнивая (1.3) и (1.6), находим выражение для свободной энергии через статистиче-

скую сумму:

βF = −ln Z. (1.7)

Перейдем от квантового выражения для статистической суммы к классическому. Для

перехода используем квазиклассический предел, выражаемый правилом Бора-Зоммер-

фельда. По этому правилу сумма переходит в интеграл с интегрированием по фазовому

пространству частиц, составляющих систему, а в силу неразличимости частиц интеграл

нужно разделить на N!, где N – число частиц системы. Таким образом, квазиклассиче-

ское выражение для статистической суммы имеет следующий вид:

Z =

−βE

,...,p

,...r

)

i=1

(2π¯h)

. (1.8)

1.2. СТАТИСТИЧЕСКАЯ СУММА 13

Если энергия системы может быть представлена аддитивно, например, в виде суммы

поступательной (E

), вращательной (E

), колебательной (E

) и электронной (E

) энер-

гий

E = E

+ E

то статистическая сумма факторизуется, т.е. она может быть представлена в виде произ-

ведений статистических сумм поступательного, вращательного, колебательного и элек-

тронного движений: Z = Z

и, соответственно, свободная энергия также пред-

ставляется в сумме свободных энергий поступательного, вращательного, колебательного

и электронного движений. Если газ не имеет внутренних степеней свободы, т.е. части-

цы газа не имеют вращательных, колебательных, электронных и других внутренних

степеней свободы, то остается только поступательное движение.

1.2.1 Статистическая сумма идеального газа

По определению идеальным газом называется система частиц, не имеющая внутренних

степеней свободы. Поэтому статистическая сумма поступательного движения и, соот-

ветственно, свободная энергия поступательного движения совпадают со статистической

суммой и свободной энергией идеального газа (Z

ид

≡ Z

). Вычислим статистическую

сумму идеального газа, или, что эквивалентно, найдем импульсную часть статистиче-

ской суммы, т.е. часть, которая определяется интегралом по импульсам частиц системы.

Для идеального газа энергия системы состоит из суммы энергий поступательного дви-

жения отдельных частиц, т.е. имеет вид

i=1

Соответственно, статистическая сумма представляется следующим интегралом:

exp

−β

i=1

(2π¯h)

Интегрирование по координате дает V

, интегралы по импульсам отдельных частиц

одинаковы, каждый из них вычисляется заменами p

= p

+ p

, dp = dp

использованием интеграла Пуассона

∞

−∞

−αx

dx =

В результате получается выражение для статистической суммы идеального газа:

Z =





2π¯h

2πm

3/2





Определим тепловую длину волны де Бройля

λ = ¯h

2πβ

14 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

тогда статистическая сумма приобретает простой вид:

Статистическая сумма выражена через переменные (T, V, N), следовательно, необходи-

мо вычислить свободную энергию системы по формуле (1.7). При вычислении исполь-

зуем формулу Стирлинга ln N! ' N ln N/e при (N À 1). Тогда получим

F = NkT ln

2π¯h

mkT

3/2

. (1.9)

Отсюда следуют выражения для термодинамических функций идеального газа, урав-

нение состояния и химического потенциала:

p = −

∂F

∂V

NkT

, (1.10)

µ =

∂F

∂N

V,T

= kT ln

Nλ

= kT ln nλ

. (1.11)

1.2.2 Статистическая сумма идеального газа с внутренними степенями

свободы

Рассмотрим частицы, находящиеся в состояниях α = 1, 2, . . . , M. Пусть в состоянии

1 со статистическим весом g

и энергией ε

находится n

частиц, в состоянии 2 – с

весом g

и энергией ε

находится n

частиц и т.д. В состоянии М со статистическим

весом g

, энергией ε

находится n

частиц. Тогда статистическая сумма внутренних

степеней свободы системы определяется формулой (1.3), где G

равно числу способов,

по которым N частиц могут быть распределены по М ячейкам, и имеет вид:

! . . . n

. . . g

энергия системы равна соответственно

E = n

+ n

+ . . . + n

а статистическая сумма

int

+···+n

=N}

! ···n

···g

−β(n

+···+n

)

Используя обобщение формулы бинома Ньютона, получаем

int

−

βε

+ g

−

βε

+ . . . + g

−

βε

= g

, (1.12)

где g является статистической суммой частицы:

g =

exp(−βε

1.2. СТАТИСТИЧЕСКАЯ СУММА 15

Суммирование производится по внутренним состояниям отдельной частицы. В резуль-

тате для идеального газа с внутренними степенями свободы статистическая сумма равна

Z = Z

int

откуда следует выражение для свободной энергии системы:

F = NkT ln

egV

2π¯h

mkT

3/2

Для газа с внутренними степенями свободы выражение для давления остается прежним

вследствие того, что импульс частицы не зависит от квантового состояния частицы, а

выражение для химического потенциала частиц сорта a имеет следующий вид:

= kT ln

. (1.13)

1.2.3 Статистическая сумма молекул

Вращательные и колебательные степени свободы молекул могут быть рассмотрены на

основе формулы (1.12). Энергия вращательного состояния с вращательным квантовым

числом J равна

= B

J(J + 1),

где B

= ¯h

/2I

, I

– момент инерции молекулы, находящейся в колебательном состоянии

v. Статистический вес состояния J равен 2J + 1, следовательно, статистическая сумма,

связанная с вращением молекулы равна

(2J + 1)e

−βB

J(J+1)

При температурах выше "комнатных" параметр βB

À 1, следовательно, основной

вклад в g

дает состояние с J À 1, поэтому при вычислении суммы суммирование

можно заменить интегрированием и считать J(J + 1) ≈ J

. В результате получим

∞

2Je

−βB

dJ =

βB

Колебания молекул в общем случае представляются ангармоническим осциллятором,

энергетические уровни которого сближаются по мере увеличения колебательного кван-

тового числа. Для большинства молекул энергия первого возбужденного колебательного

уровня, выраженная в температурных единицах, составляет тысячи градусов (напри-

мер, для N

∆ε

/k ' 3000 K, поэтому для вычисления колебательных статистических

сумм ангармонизм является несущественным, и можно рассмотреть модель гармониче-

ского осциллятора. В этой модели энергетические уровни и статистические веса опре-

деляются по формуле

= ¯hω

v +

, g

= 1 .

Статистическая сумма, связанная с колебаниями, в модели гармонического осциллятора

имеет вид

∞

v=0

−β¯hω(v+

)

16 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

Используя формулу суммирования бесконечно убывающей геометрической прогрессии

со знаменателем q = exp(−β¯hω), получаем

− 1

2sh y

, y =

β¯hω

. (1.14)

Из выражений для g

и g

могут быть найдены поправки к химическому потенциа-

лу и теплоемкостям молекулярных газов, связанные с возбуждением вращательных и

колебательных состояний.

1.3 Вириальное разложение для неидеального газа

В неидеальном газе учитывается взаимодействие между частицами, поэтому для неиде-

ального газа энергия состоит из двух частей – энергии поступательного движения ча-

стиц или кинетической энергии и потенциальной энергии, связанной со взаимным рас-

положением частиц:

i=1

+ Φ

, . . . , r

) .

Соответственно этому статистическая сумма неидеального газа является произве-

дением статистических сумм поступательного движения и статистической суммы, за-

висящей от координат частиц Z = Z

. Последняя называется конфигурационным

интегралом и имеет вид

···

exp (−βΦ

, . . . , r

))

k=1

Предположим, что потенциал взаимодействия имеет бинарный характер, т.е. все ча-

стицы взаимодействуют парами друг с другом, а взаимодействие третьей частицы не

оказывает влияния на взаимодействие между двумя выбранными частицами. Тогда

, . . . , r

) =

i<j

Кроме того, предположим, что потенциал взаимодействия между частицами является

центральным, т.е. зависящим только от относительного расстояния между частицами:

= Φ(|r

− r

|).

Тогда подынтегральное выражение конфигурационного интеграла может быть преоб-

разовано следующим образом:

−βΦ

= e

−β

i<j

(

)

i<j

−βΦ

− 1 + 1) =

i<j

(1 + f

), (1.15)

где введены функции Майера

= e

−βΦ

− 1.

1.3. ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ ДЛЯ НЕИДЕАЛЬНОГО ГАЗА 17

-1

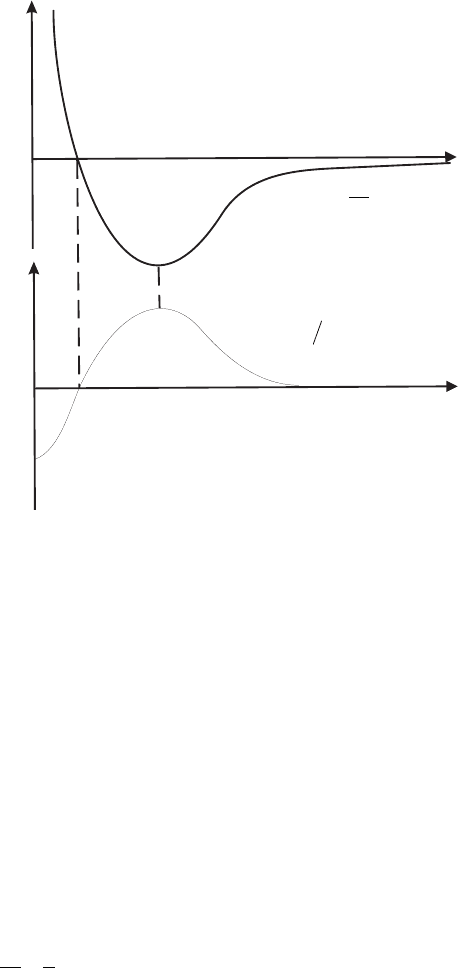
Рис. 1.2: Потенциал взаимодействия Φ(r) и функция Май-

ера f(r)

Для газа, состоящего из ней-

тральных частиц, потенциал вза-

имодействия является коротко-

действующим, т.е. на больших

расстояниях убывающим настоль-

ко быстро, что интеграл

∞

Φ(r)dr

сходится. В качестве примера от-

метим, что две заряженные части-

цы на больших расстояниях взаи-

модействуют по кулоновскому за-

кону Φ(r ) ∼ 1/r, заряд и нейтрал

на больших расстояниях притя-

гиваются вследствие взаимодей-

ствия заряда и наведенного дипо-

ля Φ(r) ∼ 1/r

, а две нейтральные

частицы на больших расстояниях

притягиваются вследствие взаи-

модействия мгновенных диполей,

Φ(r) = C/r

, где C – постоянная

Ван-дер-Ваальса. Во всех случаях

на больших расстояниях частицы

притягиваются друг к другу, т.е.

энергия взаимодействия отрицательна, а на малых расстояниях частицы отталкивают-

ся вследствие перекрытия волновых функций частиц. Качественный вид потенциала

взаимодействия частиц и соответствующая функция Майера приведены на рис. 1.2.

Отметим, что потенциал взаимодействия Φ(r) на больших расстояниях убывает сте-

пенным образом, а функция Майера экспоненциально, т.е. более быстро.

Вычисление конфигурационного интеграла возможно для так называемого случая

слабонеидеального газа. Областью действия потенциала называется расстояние порядка

a на рис. 1.2. На этом расстоянии потенциал отличен от нуля, и частицы взаимодейству-

ют друг с другом. На расстояниях r À a взаимодействие частиц отсутствует. Объем

области взаимодействия частиц 4πa

/3 можно сравнить с объемом, приходящимся на

одну частицу в газе:

πr

= 1 ,

где r

– среднее расстояние между частицами в газе. Система частиц является газом,

если r

À a или r

À a

, что эквивалентно условию na

¿ 1.

Параметр na

называется газовым параметром. При малости этого параметра ча-

стицы в основном находятся на больших по сравнению с a расстояниях, где функция

Майера близка к нулю, поэтому конфигурационный интеграл может быть найден раз-

ложением по малому параметру или по теории возмущений.

Конфигурационный интеграл может быть записан в виде произведения интегралов

по координатам всех частиц. Воспользуемся тем, что функция Майера на бесконечности

быстро убывает, поэтому область интегрирования ограничена и можно воспользоваться

разложением, предложенным Майером, т.е. представить произведение сумм в следую-

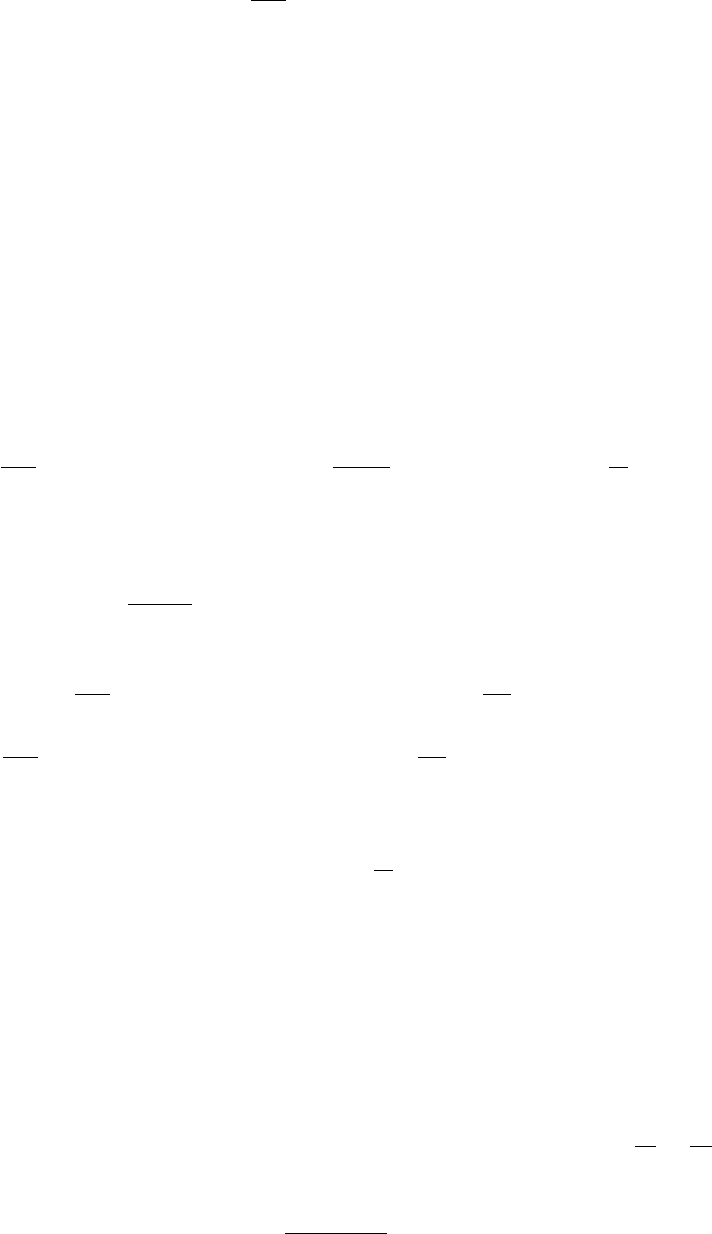
18 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

щем виде

i<j

(1 + f

)dr

···dr

i<j

(1 + f

) = (1 + f

)(1 + f

) ···(1 + f

N−1,N

) = 1 + f

+ f

+ ··· + f

N−1,N

+ f

+ ··· + f

+ f

+ ··· + f

+ ···+

+ ··· + f

···f

N−1,N

После интегрирования по координатам частиц и переобозначения переменных номера

частиц оказываются несущественными, а существенна лишь структура интеграла, за-

висящая от

1. количества функций Майера под интегралом,

2. наличия повторяющихся индексов частиц у функций Майера.

Например,

···

)dr

···dr

N−2

Z Z

)dr

f(r)dr.

Здесь вначале произведено интегрирование по всем координатам частиц кроме частиц

i, j, затем сделана замена переменных:

+ r

= R

, |r

− r

| = r, dr

= dr

dr.

Аналогично

···

)dr

· sdr

f(r)dr

···

)dr

···dr

Z Z

f(r)f

|r − r

drdr

Интегралы, содержащие функции Майера, удобно представлять в виде графов или диа-

грамм, сопоставляя

(i) ◦ − ◦ (j) ∼

(r)dr,

(i) ◦ − ◦ (j)(k) ◦ − ◦ (n) ∼ V

(r)dr

(·)dr

(i) ◦ − ◦ (j) − ◦(k) ∼

Конфигурационный интеграл может быть представлен в диаграммном виде:

= · + C

◦ − ◦ +C

◦ − ◦ − ◦ + ··· + C

◦ − ◦ −··· − ◦ = 1 + a +

+ ··· = e

где

a =

N(N − 1)

f(r)dr.

1.3. ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ ДЛЯ НЕИДЕАЛЬНОГО ГАЗА 19

При учете других типов связанных диаграмм получаем

= exp{◦ − ◦ + ◦ − ◦ − ◦···}.

Этот результат является частным случаем общей "теоремы экспонирования" в теории

графов, который выражается в том, что ряд суммы несвязных графов равен экспоненте

ряда суммы связных графов. После интегрирования по координатам и подстановки в

статистическую сумму, последний оказывается рядом по плотности. Поэтому, ограничи-

ваясь первым порядком по плотности, получим следующее разложение первых членов

статистической суммы:

Z =

N!λ

1 +

N(N − 1)

f(r)dr

Соответственно этому свободная энергия также может быть представлена в виде суммы

свободной энергии идеального газа и поправок к ней:

F = F

ид

+ ∆F, ∆F = −

kT N

где введен второй вириальный коэффициент

(T ) = −

f(r)dr.

Поправка к свободной энергии соответственно приводит к поправкам к плотности,

давлению и химическому потенциалу. Эти поправки могут быть выражены также через

второй вириальный коэффициент:

∆p = −

∂∆F

∂V

= −

T N

, или p = p

ид

(1 + nB

∆µ =

∂∆F

∂N

V,T

= −

2NkT B

= −2kT nB

Вириальный ряд был введен Камерлинг-Оннесом как ряд по плотности:

p = nkT

+ nB

+ n

+ ···

где первый вириальный коэффициент равен единице, второй вириальный коэффициент

был приведен выше, а третий вириальный коэффициент имеет более сложное выраже-

ние, связанное с произведением двух функций Майера и т.д.

Рассмотрим качественную зависимость второго вириального коэффициента от тем-

пературы:

(T ) = −

f(r)dr =

1 − e

−Φ(r)/kT

dr.

Для простого случая предположим, что потенциал имеет ступенчатый характер,

приведенный на рис. 1.3.

20 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

Рис. 1.3: Модельный потенциал взаимо-

действия частиц

Т.е. на коротких расстояниях он представля-

ет собой потенциал твердой стенки. Затем имеется

область притяжения на глубине −Φ

и на рассто-

яниях r > r

потенциал равен нулю, т.е. части-

цы на больших расстояниях не взаимодействуют.

Второй вириальный коэффициент для этого по-

тенциала имеет вид, представленный на рис. 1.3.

(T ) = −

1 − e

−βΦ

4πr

dr =

2π

−

2π

− r

´³

βΦ

− 1

при β → ∞ (T → 0) B

→ −∞ ,

при β → 0 (T → ∞) B

→

πr

При T = T

, B

= 0, что определяет температуру Бойля. При этой температуре

неидеальный газ имеет уравнение состояния, совпадающее с идеальным. Для двухпара-

метрических потенциалов типа Ленарда-Джонса второй вириальный коэффициент име-

ет аналогичный вид. При высоких температурах B

(T ) уменьшается вследствие "мяг-

кости" потенциала, т.е. уменьшения расстояния отталкивания частиц.

Ìîäåëüòâ.ñôåð

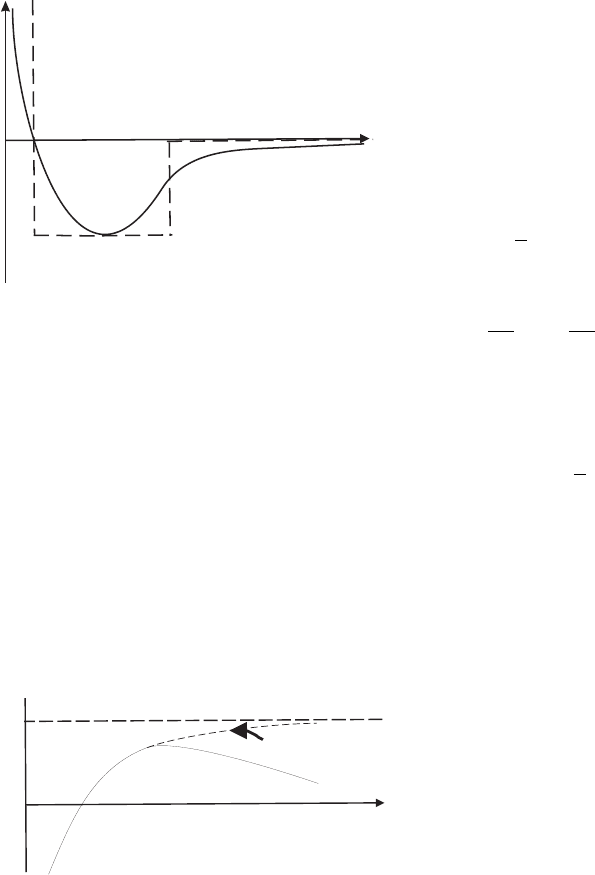
Рис. 1.4: Второй вириальный коэффициент

(T ) для реального потенциала

При низких температурах второй вири-

альный коэффициент оказывается отрица-

тельным. Это соответствует тому, что части-

цы притягиваются друг к другу и давление

снижается, т.е. давление на стенки умень-

шается из-за того, что молекулы в объеме

притягивают частицы, находящиеся в при-

поверхностном слое у стенки и давление на

стенке снижается. При повышении темпера-

туры сказывается конечность объема частиц

и, давление соответственно этому увеличи-

вается. В промежутках между двумя этими предельными случаями существует точка,

которая называется температурой Бойля. При этой температуре второй вириальный

коэффициент равен нулю, т.е. уравнение состояния совпадает с уравнением состояния

идеального газа. Это не значит, что взаимодействия нет, просто эффекты притяжения и

отталкивания компенсируют друг друга в одинаковой степени. В вириальном разложе-

нии не учитывалась возможность образования связанных состояний, т.е. если, например,

две частицы (водород и кислород) могут образовать молекулу (воды), то существование

таких молекул снижает давление идеального газа из-за того, что уменьшается количе-

ство частиц, которое оказывает давление на стенку. Кроме таких постоянных связанных

соединений могут существовать короткоживущие димеры, которые также могут сни-

жать давление идеального газа и приводить к отрицательным значениям для второго

вириального коэффициента.