Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.


3.1. УРАВНЕНИЕ БОЛЬЦМАНА 51
В состоянии термодинамического равновесия функция распределения является макс-
велловской:
f
(0)
a
(v
a
) = n
a
µ
m
a
2πkT
¶
3/2
e
−m
a
(v
a
−v
0
)
2
/2kT
. (3.11)
Соответственно концентрация и плотность компонентов смеси, среднемассовая ско-
рость и температура газа определяются выражениями:
n
a
(r, t) =
Z
f
a
(r, v
a
, t)dv
a
, n(r, t) =
X
a
n
a
(r, t), (3.12)
ρ(r, t) =
X
a
m
a
n
a
(r, t), (3.13)
v
0
(r, t) =
P
a
m
a
n
a
< v
a
>
P
b
n
b
m
b
=
1
ρ
Z
m
a
v
a
f
a
(v
a
, r, t)dv
a
, (3.14)
3
2
kT =
P
a
m
a
n
a
< (v
a
− v
0
)
2
> / 2
P
b
n
b
=
1
n
X
a
Z
m
a
(v
a
− v
0
)
2
2
f
a
(r, v
a
, t)dv
a
. (3.15)
3.1.4 Уравнения гидродинамики
Умножим уравнение Больцмана (3.10) на инвариант столкновения ψ(v
a
) и проинтегри-
руем по v
a
. Интеграл столкновений запишем в виде 4 ×(1/4)St
ab
, первый член которого
оставим без изменений, во втором произведем замену переменных (v
a
, v
b
) на (v
b
, v
a
), в
третьем – на (
˜
v
a
,
˜
v
b
), в четвертом – на (
˜
v
b
,
˜
v
a
). В результате получим
Z
St
ab
ψ(v
a
)dv
a
=
1
4
·
Z Z
ψ(v
a
)(
˜
f
a
˜
f
b
− f
a
f
b
)|v
a
− v
b
|dQ
ab
dv
b
dv
a
+
+
Z Z
ψ(v
b
)(
˜
f
b
˜
f
a
− f
b
f
a
)|v
b
− v
a
|dQ
ba
dv
a
dv
b
+
Z Z
ψ(
˜
v
a
)(f
a
f
b
−
˜
f
a
˜
f
b
)|
˜
v
a
−
˜
v
b
|d
˜
Q
ab
d
˜
v
a
d
˜
v
b
+
+
Z Z
ψ(
˜
v
b
)(f
b
f
a
−
˜
f
b
˜
f
a
)|
˜
v
b
−
˜
v
a
|d
˜
Q
ba
d
˜
v
b
d
˜
v
a
¸
=
=
1
4
Z Z
ψ(v
a
)(
˜
f
a
˜
f
b
− f
a
f
b
)|v
a
− v
b
|[ψ(v
a
) + ψ(v
b
) − ψ(
˜
v
a
) − ψ(
˜
v
b
)]dQ
ab
dv
a
dv
b
.
Для инвариантов столкновений
ψ(v
a
) + ψ(v
b
) − ψ(
˜
v
a
) − ψ(
˜
v
b
) = 0,
поэтому в результате интегрирования получим обобщенное уравнение переноса
∂ < ψ >
∂t
+ ∇ · (v
0
< ψ >) = −∇· < (v − v
0
)ψ > . (3.16)
Рассмотрим частные случаи инвариантов столкновений.
• Положим ψ(v
a
) = 1, в этом случае получаем уравнение непрерывности смеси в
целом
∂ρ
∂t
+ ∇ · ρv
0
= 0 . (3.17)
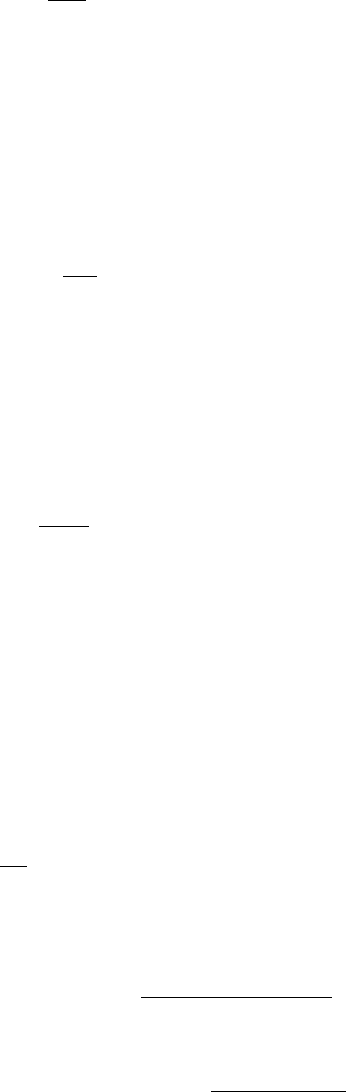
52 ГЛАВА 3. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЛАЗМЫ
• Положим ψ(v
a
) = m
a
, в этом случае получаем уравнение диффузии компонента
смеси
∂n
a
∂t
+ ∇ · n
a
v
0
= −∇ · Γ
a
, (3.18)
где диффузионный поток частиц сорта a
Γ
a
= n
a
< v
a
− v
0
> . (3.19)
Умножая уравнения диффузии на массу частицы m
a
и деля на плотность, с уче-
том уравнения неразрывности, можно получить уравнение диффузии компонент в
форме, использующейся в гидродинамике:
ρ
Ã
∂с
a
∂t
+ v
0
· ∇с
a
!
= −∇ · i
a
, (3.20)
где массовый поток частиц сорта a
i
a
= m
a
Γ
a
. (3.21)
• Положим ψ(v
a
) = m
a
v
a
– удельный импульс компонента a. В этом случае получаем
уравнение движения:
∂ρv
0
∂t
+ ∇ · ρv
0
v
0
= −∇ · P, (3.22)
где тензор напряжений
P
ik
=
X
i
m
a
n
a
< (v
ai
− v
0i
)(v
ak
− v
0k
) > (3.23)
может быть разделен на диагональную изотропную часть – давление и тензор сдви-
говых напряжений Стокса P
ik
= pδ
ik
− σ
ik
.
• Положим ψ(v
a
) = m
a
v
2
a
/2 – кинетическая энергия компонента a. В этом случае
получаем уравнение внутренней энергии:
ρ
Ã
∂u
∂t
+ v
0
· ∇u
!
= −∇ · q + ∇ · (P · v
0
), (3.24)
где внутренняя энергия единицы объема
ρu =
X
n
a
m
a
< (v
a
− v
0
)
2
>
2
, (3.25)
поток тепла
q =
X
a
n
a
*
(v
a
− v
0
)
m
a
(v
a
− v
0
)
2
2
+
. (3.26)
Таким образом, из уравнения Больцмана следуют уравнения гидродинамики, которые
являются незамкнутыми, пока не определены потоки – диффузионный поток частиц
сорта a, тензор вязких напряжений и поток тепла.

3.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ПЛАЗМЕ С НЕУПРУГИМИ ПРОЦЕССАМИ 53
3.2 Уравнения сохранения в плазме с неупругими процессами
Определения:
• m
s
- масса частиц сорта s
• n
s
- концентрация частиц сорта s
• ρ
s
= n
s
m
s
- плотность частиц сорта s
• ρ =
P
s
ρ
s
- плотность среды
• c - скорость частицы
• < ... >
s
- осреднение по функции распределения частиц сорта s
• v
s
=< c >
s
- среднечисловая (совпадает со среднемассовой) скорость компонента s
• v =
P
s
ρ
s
v
s
/ρ - среднемассовая скорость среды
• C = c − v
s
- скорость частицы сорта s в с.к. движущейся со среднемассовой скоро-
стью компонента s
• W
s
= v
s
− v - диффузионная скорость компонента s
• T
s
- температура компонента s
Для отдельных компонентов температура и давление равны
3
2
kT
s
≡
*
m
s
C
2
2
+
s
=
Z
∞
−∞
m
s
C
2
2
f
s
dC, (3.27)
p
s
= n
s
kT
s
. (3.28)
Тепловой поток компонента s
q
s
= n
s
*
C
m
s
C
2
2
+
s
. (3.29)
Тензор напряжений компонента
Π
s
= ρ
s
hCCi
s
= pI − σ
s
, (3.30)
где тензор вязких напряжений компонента
σ
s
= −(Π
s
− pI) = −ρ
s
µ
hCCi
s
−
1
3
D
C
2
E
s
I
¶
. (3.31)
Тензор вязких напряжений смеси
σ =
X
s
σ
s
= −(Π − pI). (3.32)
Уравнение Больцмана для компонента s:
∂n
s
f
s
∂t
+ c · ∇n
s
f
s
+
F
s
m
s
· n
s
∇
c
f
s
=
X
r
St
sr
. (3.33)

54 ГЛАВА 3. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЛАЗМЫ
Интеграл столкновений имеет вид
St
sr
= n
s
n
r
Z
h
f
s
(C
0
)f
r
(
˜
C
0
) − f
s
(C)f
r
(
˜
C)
i
|
˜
C − C|dQd
˜
C. (3.34)
Заменяя переменные c = C + v
s
получим уравнение Больцмана в виде
∂
∂t
(n
s
f
s
) + (v
s
+ C) ·∇(n
s
f
s
) +
Ã
F
s
m
s
−
dv
s
dt
!
n
s
·∇
C
f
s
−Cn
s
∇
C
f
s
:
dv
s
dr
=
X
r
St
sr
. (3.35)
Умножая на функцию от векторной скорости Φ(C) и интегрируя по скоростям, получим
Z
∞
−∞
Φ
"
∂
∂t
(n
s
f
s
) + (v
s
+ C) · ∇(n
s
f
s
) +
Ã
F
s
m
s
−
dv
s
dt
!
n
s
· ∇
C
f
s
− Cn
s
∇
C
f
s
:
dv
s
dr
#
dC =
=
X
r
∆
sr
[Φ] = 0 , (3.36)
где
∆
sr
[Φ] =
Z
∞
−∞
ΦdC. (3.37)
Подставляя Φ = m
s
, m
s
C и m
s
C
2
s
/2, получим уравнения сохранения для компонент:
∂ρ
s
∂t
+ ∇ · [ρ
s
(v
s
+ W
s
)] = 0 , (3.38)
d
dt
(ρ
s
W
s
) + ∇p
s
− n
s
Ã
< F
s
> −m
s
dv
s
dt
!
+ ρ
s
[W
s
(∇ · v
s
) + (W
s
· ∇)v
s
] =
=
X
r
∆
sr
[m
s
C
α
] =
X
r6=s
∆
sr
[m
s
C
α
], (3.39)
d
dt
(ρ
s
u
s
) + ∇ · q
s
− n
s
< C · F
s
>
s
+ρ
s
W
s
·
dv
s
dt
+ ρ
s
u
s
∇ · v
s
+ Π : ∇v
s
=
=
X
r
∆
sr
·
1
2
m
s
C
2
¸
=
X
r6=s
∆
sr
·
1
2
m
s
C
2
¸
, (3.40)
где внутренняя энергия газа
u
s
= u
s пост
=
1
2
< C
2
>
s
=
3
2
kT
s
m
s
.
Для газа, состоящего из частиц с внутренними степенями свободы
u
s
= u
s пост
+ u
s внутр
.
Для смеси в целом уравнения непрерывности, движения и энергии получаются сум-
мированием уравнений баланса для отдельных компонентов:
∂ρ
∂t
+ ∇ · (ρv) = 0, (3.41)
ρ
dv
dt
= −∇p + ∇ · σ +
X
s
n
s
< F
s
>, (3.42)
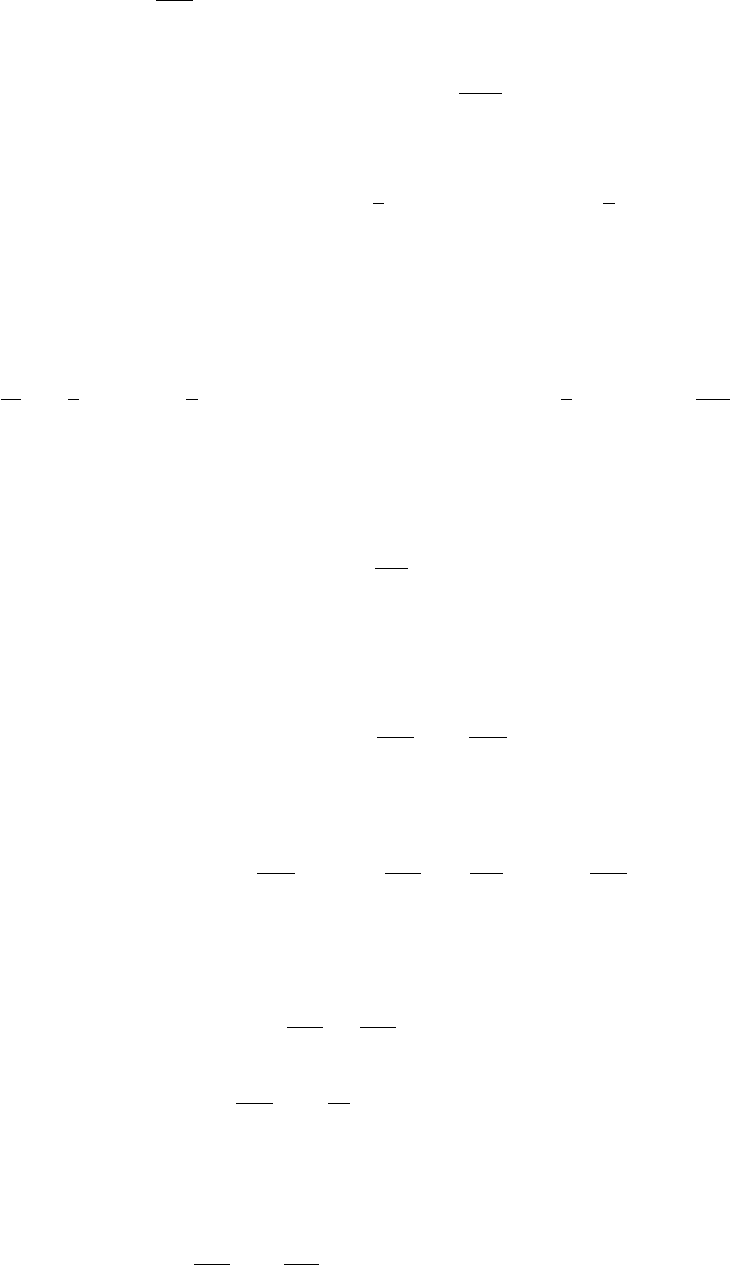
3.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ПЛАЗМЕ С НЕУПРУГИМИ ПРОЦЕССАМИ 55
dρu
dt
+ (ρu + p)∇ · v = −∇q + σ : ∇v +
X
s
n
s
< CF
s
>
s
(3.43)
где удельная внутренняя энергия газа
u =
X
s
ρ
s
u
s
ρ
.
Члены в правых частях уравнений балансов
X
s
n
s
< F
s
>=
1
c
X
s
n
s
Z
s
eW
s
× H =
1
c
j × H. (3.44)
X
s
n
s
< CF
s
>
s
= j · E
∗
. (3.45)
Применение теории [?] для электронов с учетом малости отношения масс электронов
и тяжелых частиц дает:
d
dt
µ
n
e
3
2
kT
e
¶
+ n
e
5
2
kT
e
∇ · v + ∇ · q
e
− j
e
· E
∗
= n
e
X
h
3
2
k(T
h
− T
e
)2
m
e
M
h
< ν
eh
> . (3.46)
3.2.1 Баланс энергии при учете неупругих столкновений
Неупругие столкновения существенны при
ν
ee
À
X
h
m
M
h
ν
eh
и ν
ee
À ν
eТ
.
Скорость потерь энергии электронами на единицу объема равна скорости увеличе-
ния энергии возбужденными атомами. При этом ион можно рассматривать как состоя-
ние атома с энергией возбуждения равной потенциалу ионизации
dU
e
dt
= −
dU
a
dt
.
Скорость увеличения энергии возбужденными атомами определяется скоростью обра-
зования возбужденных атомов в единице объема
dU
a
dt
=
X
k
ε
k
dn
k
dt
= I
dn
i
dt
+
0
X
k
ε
k
dn
k
dt
,
где ε
i
= I - потенциал ионизации атома.
Используя выражение для скоростей образования возбужденных атомов сорта k в
единице объема
dn
k
dt
=
∂n
s
∂t
+ ∇ · [n
s
(v + W
s
)], (3.47)
получаем
dU
e
dt
= −
∂
∂t
X
s
ε
s
n
s
− ∇ ·
X
s
ε
s
(v + W
s
). (3.48)
Для учета неупругих столкновений необходимо добавить этот член в баланс энергии
(3.46). Наибольший вклад дают ионы, т.к., аналогично обрезанию статсумм нижние
уровни атомов дают малый вклад при
ε
∗
dn
∗
dt
¿ I
dn
e
dt
, n
0
e
−I/kT
e
¿ n
e
e
−I/kT
e
¿ α ¿ 1.

56 ГЛАВА 3. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЛАЗМЫ
В результате получаем
dU
e
dt
≈ − I
∂n
i
∂t
− I∇ · [n
i
(v + W
i
)]. (3.49)
Учтем балансы числа ионов и электронов:
∂n
i
∂t
+ ∇ · [n
i
(v + W
i
)] = ˙n
i
,
∂n
e
∂t
+ ∇ · [n
e
(v + W
e
)] = ˙n
e
,
и условие электронейтральности
˙n
e
= ˙n
i
.
Из этих уравнений следует уравнение сохранения электрического заряда
∂ρ
∗
e
∂t
+ ∇ · j = 0
где объемного заряда и плотность тока равны
ρ
∗
e
= e(n
i
− n
e
), j = e(n
i
− n
e
)v + j
i
+ j
e
.
В результате получаем баланс энергии электронов с учетом неупругих столкновений
d
dt
·
n
e
µ
3
2
kT
e
+ I
¶¸
+ n
e
µ
5
2
kT
e
+ I
¶
∇ · v + ∇ ·
Ã
q
e
− I
j
e
!
− j
e
· E
∗
=
= n
e
X
h
3
2
k(T
h
− T
e
)2
m
e
M
h
< ν
eh
> . (3.50)
3.3 Метод Чепмена-Энскога
3.3.1 Коэффициенты переноса нейтральных газов
Транспортными свойствами газа, или коэффициентами переноса, называются коэффи-
циенты электропроводности, диффузии, теплопроводности и вязкости. Эти коэффици-
енты, как это следует из феноменологической теории – законов Фика, Фурье и Ньютона
и подтверждается кинетической теорией газов, являются коэффициентами пропорцио-
нальности между потоками (плотности электрического тока, массовым или числовым
потоком частиц, теплового потока и тензора вязких напряжений) и "термодинамиче-
скими силами" , к которым относятся напряженность электрического поля, градиенты
удельных или мольных концентраций, градиент температуры и тензор сдвига.
В этом параграфе рассмотрим задачи вычисления коэффициентов переноса – вяз-
кости, теплопроводности и диффузии методом Чепмена-Энскога и получим формулы,
позволяющие вычислять коэффициенты переноса нейтральных газов. Здесь будут ис-
пользоваться следующие обозначения: v – скорость молекулы, v
0
– среднемассовая ско-
рость движения среды, u = (v − v
0
)/
q
m/2kT , – безразмерная относительная скорость
молекул, u
2
= x, поэтому функция распределения Максвелла в изотропном случае мо-
жет быть записана в виде
f
(0)
(v)dv = f
(0)
(x)dx, f
(0)
(x) = n(2/
√
π)x
1/2
e
−x
. (3.51)

3.3. МЕТОД ЧЕПМЕНА-ЭНСКОГА 57
В методе Чепмена-Энскога решения уравнения Больцмана используется теория возму-
щений по числу Кнудсена, т.е. функция распределения записывается в виде
f = f
(0)
(1 + χ), (3.52)
где f
0
определяется формулой (3.11), с пространственно-временной зависимостью от
моментов n(r, t), v
0
(r, t), T (r, t). Подставляя (3.52) в уравнение Больцмана в отсутствие
внешних сил в первом порядке по числу Кнудсена, получим
∂f
(0)
∂t
+ v · ∇f
(0)
=
Z
f
(0)
(v)f
(0)
(v
1
)|v − v
1
|dQ [χ(v
0
) + χ(v
0
1
) − χ(v) − χ(v
1
)] dv
1
. (3.53)
Временные производные исключаются с помощью уравнений гидродинамики идеально-
го газа (3.17) – (3.24), где σ = 0, q = 0. В результате получается система уравнений:
f
(0)
"Ã
mv
2
2kT
−
5
2
!
v · ∇ln T +
m
kT
µ
vv −
1
3
δv
2
¶
: ∇v
0
#
=
=
Z
f
(0)
(v)f
(0)
(v
1
)|v − v
1
|dQ [χ(v
0
) + χ(v
0
1
) − χ(v) − χ(v
1
)] dv
1
. (3.54)
Вследствие условий нормировки, которым удовлетворяют функции f и f
(0)
, для функ-
ции χ должны выполняться равенства
< χ >
0
= 0 , < χv >
0
= 0 , < χ(v − v
0
)
2
>
0
= 0 . (3.55)
Обозначение <>
0
указывает, что усреднение выполняется по функции f
(0)
. Уравнение
(3.54) является неоднородным линейным уравнением. Решениями однородного уравне-
ния являются инварианты столкновений χ = 1, mv, mv
2
/2, а решение неоднородного
уравнения должно быть таким, чтобы выполнялись условия (3.55), т.е. необходимо най-
ти решения неоднородного уравнения, ортогональные к решениям однородного урав-
нения. В соответствии с методом Чепмена-Энскога решение неоднородного линейного
уравнения (3.54) ищем в виде
χ(v) = −A(u
2
)u · ∇ln T − B(u
2
)(uu −
1
3
δu
2
) : ∇v
0
.
При этом скалярные равенства (3.55) удовлетворяются тождественно, а векторное усло-
вие на функцию A(u
2
) имеет вид
Z
f
(0)
(u)u
2
A(u)
2
du =
Z
∞
0
A(x)x
3/2
e
−x
dx = 0 . (3.56)
Разложим функции A(x), B(x) в ряд по ортогональным полиномам. Возникает вопрос:
по какому набору полиномов проводить разложение? Ответ на этот вопрос заключает-
ся в следующем [15]. Набор ортогональных полиномов определяется однозначно, если
задан интервал {x}, на котором производится разложение и весовая функция на этом
интервале. В рассматриваемой задаче интервал 0 < x < ∞, а весовая функция имеет
вид (см. (3.56)) x
r
exp (−x). В этом случае полным набором ортогональных полиномов
являются полиномы Сонина-Лагерра
L
r
n
=
1
n!
e
x
x
r
d
n
dx
n
e
−x
x
−r
, L
r
n
(x) =
n
X
m=0
(−1)
m
x
m
n!Γ(n + r + 1)
m!Γ(m + r + 1)Γ(n − m + 1)
,

58 ГЛАВА 3. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЛАЗМЫ
удовлетворяющих условию нормировки
< L
r
n
|L
r
n
0
>=
Z
∞
0
e
−x
x
r
L
r
n
(x)L
r
n
0
(x)dx = δ
nn
0
n!Γ(n + r + 1). (3.57)
Напомним, что для полуцелых значений Γ
³
n +
1
2
´
= (
√
π/2
n
)(2n−1)!!. В методе Чепмена-
Энскога для коэффициентов A(x) будут использоваться полиномы с r = 3/2, а для
коэффициентов B(x) – с r = 5/2. Первые полиномы L
r
0,1
(x) имеют вид
L
3/2
0
(x) = 1, L
3/2
1
(x) =
5
2
− x, L
5/2
0
(x) = 1, L
5/2
1
(x) =
7
2
− x. (3.58)
Таким образом, ищем решение для A(x), B(x) в виде рядов
A(x) =
∞
X
n=0
A
n
L
3/2
n
(x), B(x) =
∞
X
n=0
B
n
L
5/2
n
(x). (3.59)
Найдем уравнения, определяющие A
n
. Из (3.56) с учетом (3.57) следует A
0
= 0 . Подста-
вим разложение (3.59) в (3.54):
Z
f
(0)
(u)f
(0)
(u
1
)|u − u
1
|dQ
∞
X
n=0
A
n
h
u
0
L
3/2
n
(u
02
) + u
0
1
L
3/2
n
(u
0
2
1
) − uL
3/2
n
(u
2
) − u
1
L
3/2
n
(u
2
1
)
i
×
×du
1
=
µ
u
2
−
5
2
¶
uf
(0)
(u). (3.60)
Рис. 3.1: Система координат для вычисле-
ния столкновительных интегралов
Умножая это уравнение на uL
3/2
s
(u
2
) и ин-
тегрируя по u, в правой части получим
Z
due
−u
2
u
2
µ
u
2
−
5
2
¶
L
3/2
s
(u
2
) =
=
2n
√
π
Z
∞
0
dxe
−x
x
3/2
µ
x −
5
2
¶
L
3/2
s
(x) =
= −
2n
√
π
< L
3/2
1
|L
3/2
s
>= −
2n
√
π
· 1!
µ
3
2
+ 1
¶
!δ
s1
=
= −
15
4
nδ
s1
.
Поэтому из (3.60) получаем систему уравнений,
определяющих A
r
:
∞
X
r=1
α
sr
A
r
=
15
4
nδ
s1
, (3.61)
где коэффициенты α
sr
имеют вид
α
sr
=
Z
dudu
1
f
(0)
(u)f
(0)
(u
1
)|u − u
1
|dQL
3/2
s
(u
2
)×
×
h
u · u
0
L
3/2
r
(u
0
2
) + u · u
0
1
L
3/2
r
(u
0
2
1
) − u
2
L
3/2
r
(u
2
) − u · u
1
L
3/2
r
(u
2
1
)
i
.

3.3. МЕТОД ЧЕПМЕНА-ЭНСКОГА 59
В приближении, когда учитывается один полином Сонина-Лагерра (3.59)
A
1
=
15
4
n
α
11
, (3.62)
α
11
=
n
2
π
3
Z
dudu
1
|u − u
1
|dQe
−(u
2
+u
2
1
)
u
2
h
u · u
0
u
0
2
+ u · u
0
1
u
0
2
1
− u
4
− u · u
1
u
2
1
i
.
Член, содержащий 5/2 в L
3/2
1
, сокращается. Вычисления α
11
проводятся в системе центра
масс v = v − v
1
, w = (1/2)(v + v
1
) = (1/2)(v
0
+ v
0
1
). В процессе столкновения центр
масс сохраняет свою скорость, и сохраняется модуль относительной скорости, вектор
относительной скорости поворачивается в направлении n на угол рассеяния ϑ. В этих
переменных скорости частиц до и после столкновения определяются формулами:
u = w +
1
2
v, u
0
= w +
1
2
vn, u
1
= w −
1
2
v, u
0
1
= w −
1
2
vn, dudu
1
= dvdw. (3.63)
Тогда выражение, содержащееся в α
11
, преобразуется следующим образом:
u · u
0
1
u
0
2
+ u · u
0
1
u
0
2
− u
4
− u · u
1
u
2
1
=
=
1
2
(v · n)(w · n)v
2
+ 2(w · n)
2
v
2
− 2(v · w)
2
− v
2
(v · w).
Переходя в выражении α
11
к переменным w, v , можно провести усреднение (интегри-
рование) по направлениям вектора w. В результате получается
(v · n)(w · n)v
2
+ 2(wn)
2
v
2
− 2(vw)
2
− v
2
(vw) = −
2
3
v
4
w
2
(1 − cos
2
ϑ).
Приведем пример усреднения одного из членов:
(v · w)(n · w) = v
2
w
2
cos ϑ
1
(sin ϑ
1
sin ϕ
1
sin ϑ + cos ϑ
1
cos ϑ) =
1
3
v
2
w
2
cos ϑ.
Интегрирование выполняется в системе координат, приведенной на рис. 3.1, в кото-
рой ось z направлена по вектору v, вектор n лежит в плоскости yz, ϑ - угол рассеяния,
а вектор w имеет угловые координаты ϑ
1
, ϕ. Введем обозначение сечения рассеяния
порядка l:
Q
(l)
(v) =
Z
(1 − cos
l
ϑ)dQ. (3.64)
При l = 1 это "транспортное" , или "диффузионное" сечение рассеяния, при l = 2 –
"вязкостное" , эти названия связаны с тем, что коэффициенты переноса выражаются
через соответствующие сечения. После подстановок в выражение α
11
получаем
α
11
= −
n
2
24π
3
Z
dww
2
e
−w
2
Z
dvv
5
e
−v
2
/2
Q
(2)
(v). (3.65)
Определим столкновительные интегралы
Ω
(l,s)
(T ) =
s
kT
2πµ
ab
Z
∞
0
dxe
−x
2
x
2s+3
Q
(l)
Ã
x
s
2kT
µ
ab
!
, (3.66)

60 ГЛАВА 3. КИНЕТИЧЕСКАЯ ТЕОРИЯ ГАЗОВ И ПЛАЗМЫ
где µ
ab
= m
a
m
b
/(m
a
+m
b
) – приведенная масса взаимодействующих частиц. Ω
(l,s)
имеют
размерность v
T
Q, так что nΩ
(l,s)
является эффективной частотой столкновений. Инте-
грируя (3.65) по w и используя (3.66), получаем
α
11
= −4n
2
r
m
2kT
Ω
(2.2)
(T ), A
1
= −
15
16
s
2kT
m
1
nΩ
(2.2)
(T )
.
Перейдем к вычислению B, считая в (3.54) температуру постоянной, а скорость v
0
– за-
висящей от координаты. Подставим разложение (3.60) в (3.54). Дополнительного огра-
ничения типа (3.56) для коэффициентов B
n
нет, поэтому в разложение входит член
r = 0. Умножим (3.54) на u
i
u
k
L
5/2
s
(u
2
) и проинтегрируем по u. В правой части равен-
ства получим
2
Z
duu
i
u
k
µ
u
i
u
k
−
1
3
δ
ik
u
2
¶
f
(0)
(u)L
5/2
s
(u
2
) =
8n
3
√
π
Z
∞
0
dxx
5/2
e
−x
L
5/2
s
(x).
Учитывая определение (3.58) и нормировку (3.56), находим, что это выражение равно
8n
3
√
π
< L
5/2
0
|L
5/2
s
>= 5nδ
s0
,
тогда уравнение (3.54) имеет вид
∞
X
r=0
β
rs
B
r
= 5nδ
s0
. (3.67)
Вычислим коэффициент разложения β
00
аналогично α
11
:
β
00
= −
n
2
π
3
Z
dudu
1
|u − u
1
|dQe
−(u
2
+u
2
1
)
[(u · u
0
1
)
2
+ (u · u
0
)
2
− (u · u
1
)
2
− u
4
].
После замены переменных (3.63) выражение в квадратных скобках становится равным
2
15
[(w · n)
2
v
2
+ 2(w · n)(v · n)v
2
− (w · v)
2
− 2v
2
(w · v) + (v · n)
2
v
2
− v
4
].
После усреднения по направлениям вектора w это выражение дает −(v
4
/8)(1 − cos
2
ϑ).
Учитывая определение сечений (3.64), получаем
β
00
=
n
2
64π
3
Z
dwe
−w
2
/2
Z
dv · v
5
e
−v
2
/2
Q
(2)
(v).
Интегрируя по w и выражая ответ через Ω
(l,s)
– интегралы (3.66), получаем
β
00
= 4 n
2
Ω
(2.2)
, B
0
=
5
4n
2
Ω
(2.2)
(T )
.
Решение кинетического уравнения, учитывающего первые члены полиномов разложе-
ния L
3/2
1
и L
5/2
0
с учетом A
1
, B
0
имеет вид
χ(v) =
1
nΩ
(2.2)
·
15
16
µ
mv
2kT
−
5
2
¶
v · ∇ln T −
5
8
m
kT
µ
vv −
1
3
δv
2
¶
: ∇v
0
¸
. (3.68)
