Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.

1.5. ХИМИЧЕСКОЕ РАВНОВЕСИЕ 31
ионов, т.е. выполняется условие электронейтральности n
e
= n
i
. Перейдем к переменной,
представляющей полное количество частиц, если бы все частицы были идеальными под-
системами:
n
0
=
p
id
kT
= n
e
+ n
i
+ n
a
= 2 n
e
+ n
a
.
Выразим концентрации атомов, ионов и электронов через степень ионизации и полное
число частиц n
0
:
n
a
=
1 − α
1 + α
n
0
, n
e
=
α
1 + α
n
0
.
Учитывая поправку к давлению в слабонеидеальной плазме
p = p
id
+ ∆p = p
id
(1 −
Γ
D
6
),
получаем
K
p
= K
(0)
p
(1 −
Γ
D
6
)e
Γ
D
,
можно выразить p
id
через давление и получить уравнение ионизационного равновесия
в виде
α
2
1 − α
2
=
kT
p
id
λ
3
e
g
e
g
i
g
0
a
e
−β(I−∆I)
.
Выражение для тепловой длины волны де Бройля электронов имеет в практических
единицах следующий вид:
1
λ
3
e
= 3 .0218 ∗ 10
21
T
3/2
eV
, g
e
= 2 ,
тогда уравнение Саха можно представить в следующих практически удобных единицах:
α
2
1 − α
2
= 21.1
g
i
T
5/2
3
η
Γ
D
g
0
i
p
атм
e
−I/kT
, η
Γ
D
= (1 − Γ
D
/6)e
Γ
D
.
1.5.3 Проблема ограничения статистических сумм
Рассмотрим простейший случай вычисления статистической суммы атома водорода.
Уровни энергии атома водорода определяются формулой I = Ry/m
2
, а их статисти-
ческие веса g
m
= 2m
2
. Здесь Ry = e
2
/2a
0
– постоянная Ридберга. Статистическая сумма
атома водорода равна
g
H
=
∞
X
m=1
g
m
e
−βε
m
,
или, подставляя значения уровней энергии и их статистических весов, получаем
g
H
=
∞
X
m=1
2m
2
e
−βRy/m
2
.
представляя в виде ряда:
g
H
= 2( e
−βRy
+ 4e
−βRy/4
+ 9e
−βRy/9
+ . . .).
Переходя к пределу по главному квантовому числу m → ∞, получаем lim m
2
e
−βRy/m
2
=
∞, видим, что этот ряд расходится. Расходимость ряда является асимптотической, т.е.
32 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ
такой, при которой сумма ряда зависит от числа учтенных членов. Эта расходимость из-
вестна как расходимость статистической суммы атома. Существуют различные способы
ограничения или обрезания статистических сумм. В основном здесь будут рассматри-
ваться физические методы обрезания статистических сумм.
• Э. Ферми предложил обрезать статистическую сумму на среднем расстоянии меж-
ду частицами, r
0
= n
1/3
, т.е., если атом находится в возбужденном состоянии, то
радиус его электронной орбиты увеличивается пропорционально квадрату главно-
го квантового числа. Следовательно, при больших квантовых числах радиус элек-
тронной орбиты увеличивается настолько, что квантовые орбиты двух соседних
частиц начинают пересекаться. Это означает, что электрон, который находится на
этом квантовом уровне, принадлежит одновременно обеим частицам, т.е. является
свободным. Отсюда следует следующая формула для обрезания:
e
2
r
0
=
Ry
m
2
max
.
Обрезание, или главное максимальное квантовое число, на котором обрезается ста-
тистическая сумма, определяется по формуле:
m
max
=
Ã
I
e
2
/a
0
!
1/2
Ã
3
4πna
3
0
!
1/6
.
• Ограничение по методу Инглисса-Теллера состоит в том, что вследствие эффек-
та Штарка происходит сдвиг уровня для линейного эффекта Штарка на величину
∆ε
m
=
~
d
m
·E = ea
m
E = em
2
a
0
E. Здесь d
m
= ea
m
- дипольный момент атома в m-м
состоянии. Оценим электрическое поле в плазме, связанное с наличием заряжен-
ных частиц. Электрическое поле в плазме возникает вследствие наличия других
заряженных частиц, которые перемещаются и тем самым создают флуктуирующее
электрическое поле. Это электрическое поле является статистической величиной,
среднее значение которого определяется по формуле
E ∼
e
r
0
= en
2/3
charge
,
где r
0
– среднее расстояние между заряженными частицами. Отсюда следует, что
уровень энергии атома сдвинут в среднем на величину em
2
a
0
E, но, вследствие ста-
тистичности электрического поля вместо сдвига уровня происходит его уширение.
Если это уширение уровня становится сравнимым с расстоянием между уровня-
ми, верхние уровни начинают сливаться, и, таким образом, дискретный спектр
заканчивается на уровне m
max
, который определяется равенством между ушире-
нием уровня в статистическом поле и расстоянием между уровнями. Подставляя
величину статистического электрического поля в плазме в выражение для ушире-
ния уровня вследствие эффекта Штарка и приравнивая эту величину расстоянию
между уровнями
∆ε
st
m
=
dε
m
dm
=
2Ry
m
3
,
получаем:
e
2
a
0
n
2/3
m
2
=
2Ry
m
3
=
2e
2
a
0
m
3
, m
5
max
=
2
a
2
0
n
2/3
.
1.6. СИСТЕМА ТЕРМОДИНАМИЧЕСКИХ УРАВНЕНИЙ 33
Отсюда находим уровень обрезания для метода Инглисса-Теллера:
m
max
= 2
1/5
(na
3
0
)
−2/15
I
1/5
или m
max
=
µ
2Ia
0
e
2
¶
1/5
Ã
3
4πna
3
0
!
2/15
. (1.26)
Отличия формул Ферми и Инглиса-Теллера невелики. Отметим, что оба эти обре-
зания определяются только концентрацией заряженных частиц.
• Дебаевское обрезание состоит в том, что вследствие кулоновской неидеальности
происходит снижение потенциала ионизации на величину ∆I = Γ
D
T , поэтому ка-
жется разумным m
max
определить из формулы:
Ry
m
2
max
= Γ
D
kT.
Отсюда следует уровень обрезания в данном случае:
m
max
= (
I
Γ
D
kT
)
1/2
.
• Ограничение по методу Планка-Ларкина. Более строгая теория, основанная на раз-
ложениях типа Майера для неидеальных газов дает результат, который известен
как формула Планка-Ларкина. Эта формула основана на том, что ряд для стати-
стической суммы расходится:
g =
∞
X
m=1
2m
2
e
−βI/m
2
=
∞
X
m=1
2m
2
1 −
βI
m
2
+
Ã
βI
m
2
!
2
− . . .
.
Если из этого ряда вычесть первые члены, тогда оставшаяся сумма ряда будет
сходящаяся. Поэтому формально вычитая из экспоненциального ряда два члена,
получим сходящуюся статистическую сумму. Это выражение для статистической
суммы обосновывается строго по теории возмущений, основанной на методах кван-
товой статистической физики:
g
0
a
=
∞
X
m=1
g
m
(e
−βε
m
− 1 + βε
m
).
1.6 Система термодинамических уравнений
Задача термодинамического описания газовой смеси обычно ставится следующим об-
разом: при заданных давлении, температуре и объемных или весовых соотношениях
компонентов необходимо определить концентрации частиц и термодинамические функ-
ции системы. Приведем пример. Если рассматривается смесь, в которую входят три
химических элемента – углерод, водород, азот и кислород, то эти химические элементы
при температурах в тысячи градусов и выше образуют большое количество компонен-
тов, таких как CO
2
, H
2
, O, NO, N
2
, C
+
, e и т.д. Поэтому можно использовать описание,
основанное на химических элементах, т.е. если ввести u
iα
как число атомов элемента α
в компоненте i, то можно найти число атомов элемента α в газе, которое сохраняется.
34 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ
Ядерные реакции при этом не рассматриваются, поэтому количество ядер химических
элементов и их относительные доли
β
α
=
P
i
n
i
m
α
u
iα
P
β
P
i
n
k
m
β
u
β
сохраняются постоянными. Следующее уравнение, входящее в систему термодинамиче-
ских уравнений, – это уравнение электронейтральности. Поскольку исходная смесь была
электронейтральной, то сумма количества компонентов на зарядовые числа компонен-
тов равна нулю. Это уравнение известно как уравнение электронейтральности среды в
среднем
P
i
n
i
Z
i
= 0 . При заданном давлении в газе оно определяется по сумме идеально-
го давления и поправки на неидеальность. Идеальное давление определяется по уравне-
нию Клапейрона, а поправки зависят от вида неидеальности – кулоновской, неидеаль-
ности нейтральных компонентов, или неидеальности, определяемой взаимодействием
заряженных и нейтральных частиц. Система термодинамических уравнений включает
уравнения:
• заданных пропорций химических элементов β
α
=
P
i
n
i
m
α
u
iα
/
P
γ
P
i
n
i
m
γ
u
iγ
,
• уравнение электронейтральности
P
i
n
i
Z
i
= 0 ,
• уравнение состояния p{n
i
} = p
ид
+ ∆p =
P
i
n
i
kT + ∆p{n
i
},
• для химической реакции, например, A
*
)
A + B уравнение химического равновесия
P
a
ν
a
µ
a
= 0 имеет вид
n
a
n
b
n
ab
=
g
0
a
g
0
b
g
ab
λ
3
ab
λ
3
a
λ
3
b
exp(−βI
ab
+ β∆µ
ab
− β∆µ
a
− β∆µ
b
).
В результате решения этой системы уравнений определяется равновесный состав газа,
т.е. концентрации всех компонент. По найденному составу вычисляются термодинами-
ческие функции – плотность, внутренняя энергия, энтальпия, энтропия и др.:
ρ =
X
i
n
i
m
i
,
h =
1
ρ
X
i
n
i
µ
5
2
kT + h
int
+ ∆h
¶
,
где удельная энтальпия внутренних степеней свободы равна
ρh
int
= ε
возб
i
) +
(+)
X
i
n
i
I
(1)
i
+
(++)
X
i
n
i
(I
(1)
i
+ I
(2)
i
) + . . .
+ . . . −
0
X
i
n
i
D
i
−
00
X
i
n
i
ε
i
+
000
X
i
n
i
(I
(1)
i
− D
(+)
i
,
T s = h −
X
i
N
i
µ
i
= ρ
−1
X
i
n
i
(
5
2
kT + ε
возб
i
− ln(
n
i
λ
3
i
g
0
i
− ∆µ
i
) + ∆h,
где энергия возбуждения
ε
возб
i
= T
2
d ln g
0
i
T
.
1.6. СИСТЕМА ТЕРМОДИНАМИЧЕСКИХ УРАВНЕНИЙ 35
Отметим, что полное число уравнений в термодинамической системе состоит из R +
(N − R − 2) + 1 + 1 = N уравнений, т.е. количество уравнений совпадает с количе-
ством неизвестных. Следовательно, эта система является замкнутой. Существенный во-
прос состоит в том, имеет ли эта система решение и является ли это решение един-
ственным. Приведенная система уравнений была записана через концентрации частиц
и условия химического равновесия, но выражение для давления и условие химического
равновесия являются условиями экстремума термодинамического потенциала Φ, поэто-
му та же самая система уравнений может быть сформулирована по-другому: в виде
экстремальности термодинамического потенциала по его переменным – числу частиц,
давлению, температуре. Поверхность термодинамического потенциала в соответствии с
неравенством Гиббса-Боголюбова для идеального газа является выпуклой, а уравнение
электронейтральности представляет собой уравнение нормали к данной поверхности.
Приближая плоскость с заданной нормалью к выпуклой поверхности, получаем каса-
ние в одной точке, координаты которой являются решением данной системы уравнений.
Это доказательство единственности решения термодинамической системы уравнений
для идеального газа было проведено Я.Б. Зельдовичем. Для неидеального газа, где
существуют поправки на взаимодействие, которые корректно обоснованы только при
малых параметрах взаимодействия, теорема Зельдовича о единственности решения мо-
жет нарушаться. В качестве примера можно привести пример неидеальной плазмы при
большом значении параметра неидеальности и малых степенях ионизации (Γ
D
> 1,
α ¿ 1), где термодинамический потенциал не является выпуклым, и система может
иметь три решения. Одно из этих решений соответствует состоянию неустойчивой фазы,
т.е. возможному плазменному переходу, аналогично фазовому переходу газ-жидкость
(Н.Н.Калиткин).
36 ГЛАВА 1. ТЕРМОДИНАМИКА ГАЗОВ И ПЛАЗМЫ

Глава 2
ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ В
ГАЗАХ И ПЛАЗМЕ
В настоящей главе рассматриваются элементарные процессы в газах и плазме. Под эле-
ментарными процессами понимаются упругие и неупругие столкновения атомных ча-
стиц. В курсе лекций по физической механике будут рассматриваться только упругие
столкновения частиц, поскольку они определяют процессы переноса массы, импульса и
энергии. Неупругие процессы определяют скорости химических реакций в газе и перенос
энергии, связанный с внутренними степенями свободы частиц.
2.1 Дифференциальные сечения рассеяния частиц
Рассмотрим рассеяние частиц, потенциал взаимодействия которых Φ(r) является корот-
кодействующим. Пусть на рассеивающую частицу падает поток частиц n
1
v
rel
, которые
с некоторой вероятностью рассеиваются на различные углы, соответствующую диф-
ференциальную вероятность рассеяния в единицу времени обозначим dW (v, χ). Диф-
ференциальным сечением по определению называется отношение дифференциальной
вероятности к потоку падающих частиц:
dQ(v, χ) =
dW (v, χ)
n
1
v
rel
. (2.1)
В квантовой теории дифференциальная вероятность определяется "золотым правилом
квантовой механики" :
dW =
2π
h
|Φ
12
|
2
. (2.2)
В классической теории при выполнении условия a À λ, где a – область действия по-
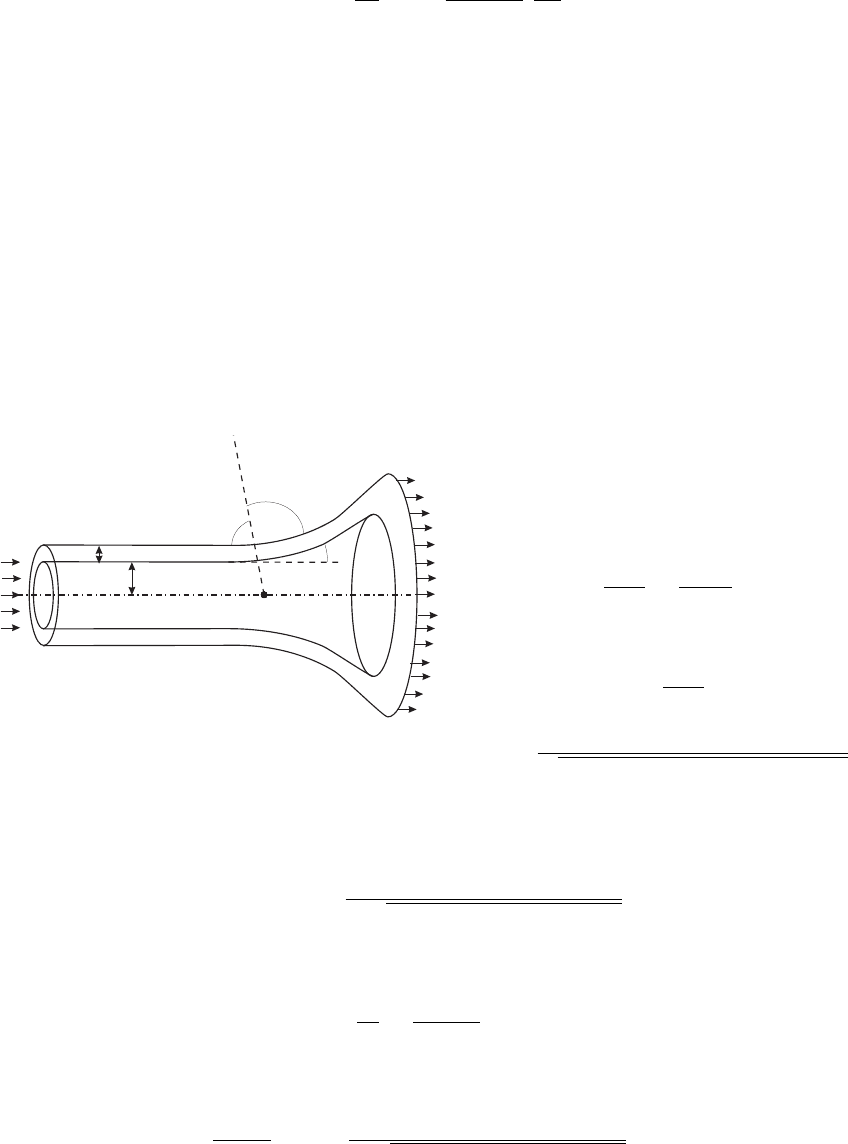
тенциала, λ – длина волны де-Бройля эта вероятность, как следует из рис. 2.1 равна
количеству частиц, попадающих в единицу времени в кольцо с радиусами
ρ
и
ρ
+
dρ
:
dW = 2πρdρv
rel
n
1
.
Подставляя это выражение в формулу (2.1), получаем
dQ = 2π ρdρ.
37
38 ГЛАВА 2. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ В ГАЗАХ И ПЛАЗМЕ
Можно перейти к зависимости от угла рассеяния:
dQ = 2πρ|
dρ
do
|do =
2πρ
2π sin χ
|
dρ
dχ
|do,
т.к. do = 2π sin χdχ. Используя дифференциальное сечение, определим сечение порядка
l:
Q
(l)
(v) =
Z
(1 − cos
l
χ)dσ.
При l = 1 это сечение называется транспортным, или диффузионным, сечением, при
l = 2 – вязкостным, поскольку соответствующие сечения определяют коэффициенты
переноса – диффузию и вязкость газа.
2.2 Классическая задача теории рассеяния
Классическая задача рассеяния частицы с массой m
1
на частице m
2
, взаимодействую-
щих с потенциалом Φ(r), сводится к задаче рассеяния частицы с приведенной массой
m = m
1
m
2
/(m
1
+ m
2
) в том же потенциале.
f
0
f
0
r
dr
n,V
îòí
c
Рис. 2.1: Классическое рассеяние частиц
В центральном поле сохраняется
кинетический момент l = mr
2
˙ϕ = const
(первый интеграл движения). Исполь-
зуя второй интеграл движения – пол-
ную энергию частиц
E =
m ˙r
2
2
+
l
2
2mr
2
+ Φ(r ),
получаем
dt =
mr
2
l
dϕ =
=
dr
q
2E/m − l
2
/m
2
r
2
− 2Φ(r)/m
.
Перейдем от переменных (E, l) к (v
∞
, ρ). Далее положим v
∞
= v, тогда E = mv
2
/2,
l = mvρ, угол рассеяния
ϕ
0
(ρ) =
Z
∞
r
0
ρdr
r
2
q
1 − ρ
2
/r
2
− 2Φ(r ) /mv
2
,
где r
0
является корнем уравнения ˙r
0
= 0 или
1 −
ρ
2
r
0
−
2Φ(
r
0
)
mv
2
= 0 .
Из рис. 2.1 следует 2ϕ
0
+ χ = π, поэтому функция ρ(χ) определяется уравнением
π − χ
2
=
Z
∞
r
0
ρdr
r
2
q
1 − ρ
2
/r
2
− 2Φ(r ) /mv
2
. (2.3)
Из этого уравнения определяется функция ρ = ρ(χ, v), по которой определяется диф-
ференциальное dQ и затем – парциальные сечения рассеяния Q
(l)
(v).
2.2. КЛАССИЧЕСКАЯ ЗАДАЧА ТЕОРИИ РАССЕЯНИЯ 39
2.2.1 Классические траектории
Зависимость потенциала взаимодействия частиц от расстояния для реальных газов по-
казана на рис. 1.2. Основываясь на этой зависимости, рассмотрим поведение угла рас-
сеяния в зависимости от прицельного параметра ρ. При малых значениях прицельного
параметра угол рассеяния равен π, поскольку при этом происходит прямое отражение
частицы. При больших значениях прицельного параметра угол рассеяния мал и отри-
цателен вследствие притяжения частиц на больших расстояниях. Между этими двумя
предельными случаями функция χ(ρ), если она является непрерывной, имеет хотя бы
одно нулевое значение.
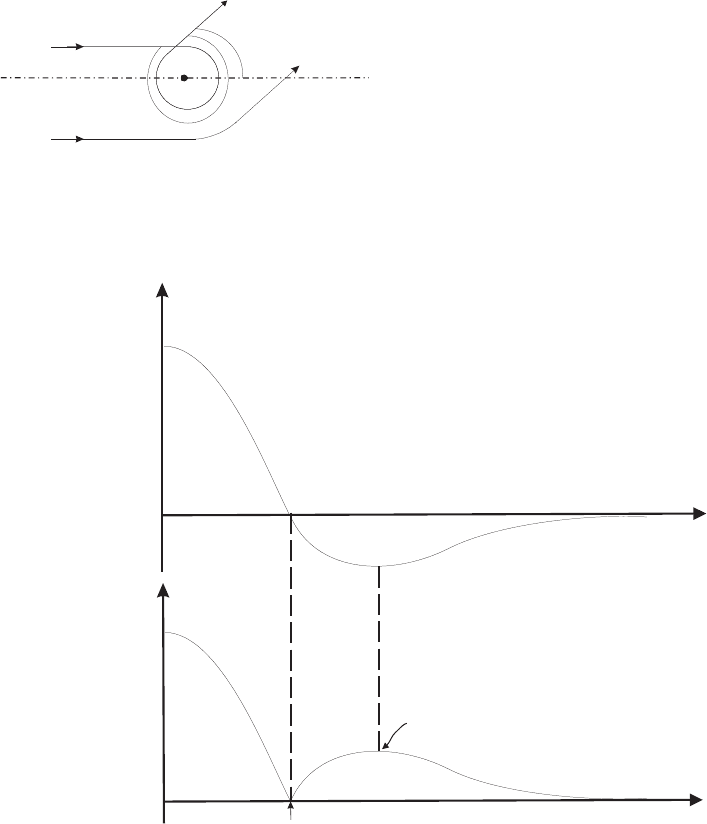
q
c
1
2
2
1
Рис. 2.2: Определение углов рассеяния частиц
В экспериментальных наблюдениях уг-
ловой зависимости рассеянных частиц ис-
пользуется прибор Рамзауера, который со-
стоит из нескольких детекторов, располо-
женных под различными углами, регистри-
рующих рассеянные частицы. Эти детек-
торы не различают частицы, испытавшие
несколько оборотов частиц (см. рис. 2.3), по-
этому удобно ввести новый угол рассеяния
ϑ(ρ), который изменяется от 0 до π.
r
p
p
q
c
glory
rainbow
0
0
Рис. 2.3: Зависимость χ( ρ)(верхняя кривая) и ϑ(ρ) (нижняя кривая) для реального потенциала
Зависимость углов рассеяния χ(ρ) и ϑ(ρ) от прицельного параметра показана на
рис. 2.3. Существуют два случая рассеяния, известные как "сияние" и "радужное" ,
представленные на рис. 2.3.
40 ГЛАВА 2. ЭЛЕМЕНТАРНЫЕ ПРОЦЕССЫ В ГАЗАХ И ПЛАЗМЕ
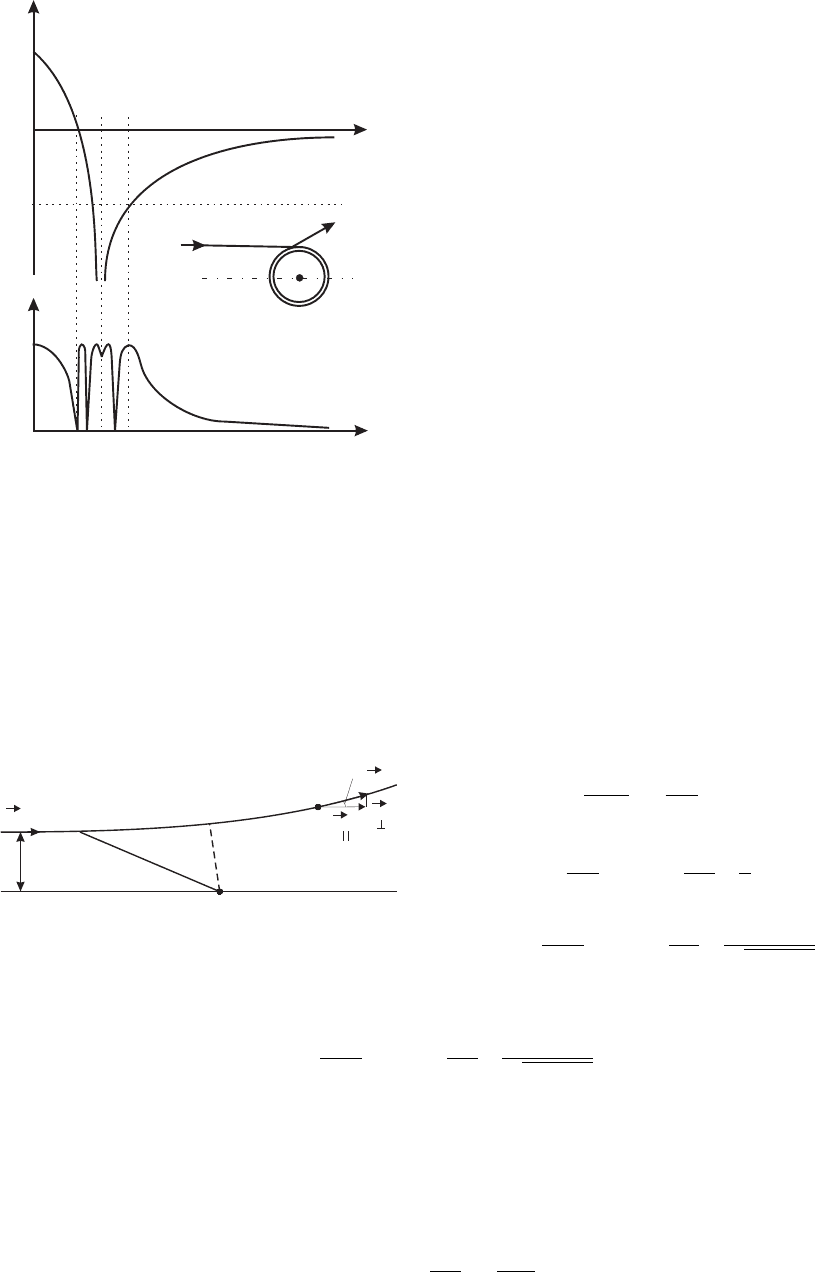
c
p
-p-p
p
u
r
r
Рис. 2.4: Траектории "орбитирования" в за-
висимости χ(ρ) и ϑ(ρ)
Для случая "сияния" частица не изменя-
ет своего направления движения, несмотря на
то, что на части траектории находится в поле
действия потенциала. В задаче о распростране-
нии света в каплях в атмосфере это приводит
к эффекту "сияния" . "Радужный" угол рассе-
яния соответствует максимуму функции ϑ(ρ),
или бифуркации, при которой происходит пере-
ход от одного к трем корням зависимости ρ(ϑ).
В оптике этот эффект приводит к возникнове-
нию радуги.
Функция χ(ρ) вообще говоря, при некото-
ром прицельном расстоянии может обращать-
ся в бесконечность, что соответствует тому, что
при некотором прицельном расстоянии притя-
жение компенсируется отталкиванием, т.е. про-
исходит "захват" частицы, или "орбитирова-
ние" , показанное на рис. 2.4.
Эти результаты демонстрируют сложность
проблемы рассеяния даже в случае классиче-
ской механики.
2.2.2 Кулоновское рассеяние. Формула Резерфорда
Рассмотрим рассеяние на малые углы в короткодействующем потенциале или для даль-
нодействующих потенциалов рассеяния, справедливое почти для всех прицельных па-
раметров. Угол рассеяния в этом случае можно определить по отношению изменения
поперечного импульса к продольному импульсу рассеивающейся частицы:
V
r
r
c
p
p
p
Рис. 2.5: Рассеяние на малые углы для дально-
действующего потенциала
χ =
∆p
⊥
p
k
=
1
mv
Z
F
⊥
dt =
=
2
mv
Z
∞
ρ
Ã
−
∂Φ
∂r
!
ρ
r
dt =
=
2ρ
mv
2
Z
∞
ρ
Ã
−
∂Φ
∂r
!
dr
√
r
2
− ρ
2
,
где r
2
= ρ
2
+ v
2
t
2
. Переходя от t к r, получим
χ =
2ρ
mv
2
Z
∞
ρ
Ã
−
∂Φ
∂r
!
dr
√
r
2
− ρ
2
. (2.4)
Эта формула может быть получена разложением решения точной задачи рассеяния (2.3)
по потенциалу взаимодействия.
Формула (2.4) наиболее подходит для определения сечения рассеяния в кулоновском
потенциале Φ = Ze
2
/r. Производная по координате от потенциала равна силе, действу-
ющей на частицу:
F (r) = −
∂Φ
∂r
=
Ze
2
r
2
.
