Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.

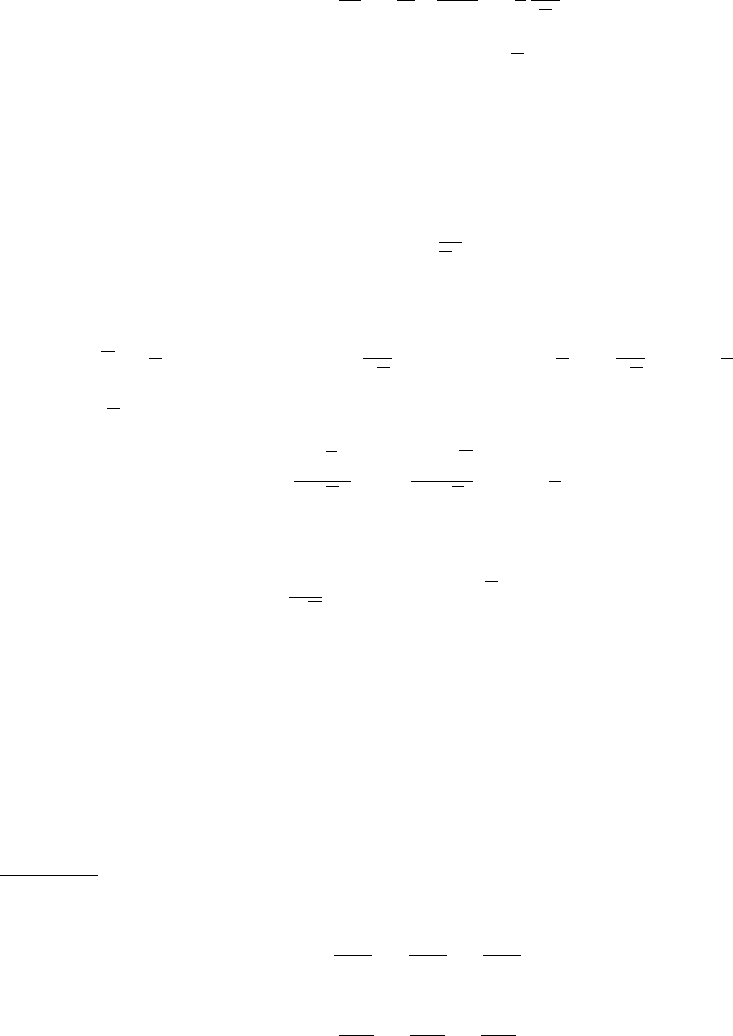
6.5. НЕОДНОРОДНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 201
Здесь ξ = y/R - безразмерная радиальная координата, которая связана с координатой
η следующим соотношением:
η =
y
y
∗
=
y
R
·
Ru
∗
ν
=
ξ
2
Re
u
. (6.129)
Здесь введено среднее число Рейнольдса Re = 2R/u/ν. При вязком течении в трубе из
баланса сил, действующих на трубу, имеем:
2πRLτ(0) = πR
2
∆p,
где τ(0) = τ = ρu
2
∗
- напряжение трения на стенке. Подставляя ∆p в (6.127), получаем
λ =
8
u
2
.
Подставляя в (6.128) логарифмический профиль скоростей (6.125), находим:
u =
2
κ
Z
1
0
µ
ln ξ + κ + ln
µ
Re
2u
¶¶
(1 − ξ)dξ =
1
κ
µ
ln
Re
2u
+ κ −
3
2
¶
.
Выражая u через коэффициент сопротивления, находим искомую зависимость λ(Re):
2
√
2κ
√
λ
= ln
Re
√
λ
4
√
2
+ κ −
3
2
,
или после подстановки численных значений:
1
√
λ
= 2.035 lg Re
√
λ − 0.91. (6.130)
Этот результат хорошо подтверждается экспериментально, переходя при R e < 10
5
в
формулу Блазиуса:
λ = 0 .3164Re
−1/4
. (6.131)
Задача 2. Найти изменение характеристик турбулентного потока (кинети-
ческой пульсационной энергии вдоль различных осей координат) при быст-
рой деформации потока за время, меньшее времени релаксации вязких сил.
(Дж.К.Бэтчелор [33]).
Решение. По определению вихревой линиии [52] до и после деформации компоненты
вектора завихренности (~ω = ∇ ×~v) удовлетворяют уравнениям:
da
1
ω
(0)
1
=
da
2
ω
(0)
2
=
da
3
ω
(0)
3
, (6.132)
dx
1
ω
1
=
dx
2
ω
2
=
dx
3
ω
3
, (6.133)
где a
i
, x
i
- координаты до и после деформации, связанные тензором деформации S
ij
=
∂x
i
/∂a
j
, который в системе координат, совпадающей с главными осями деформации име-
ет диагональный вид S
ij
= e
(i)
δ
ij
(по индексу в скобках не суммируется). Из уравнения
непрерывности следует
e
1
e
2
e
3
= ρ
0
/ρ,

202 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ
где ρ
0
и ρ - начальная и текущая плотности. Уравнение движения вихря в отсутствие
вязких сил имеет вид [52]:
d
dtb
Ã
~ω
ρ
!
=
ÃÃ
~ω
ρ
!
· ∇
!
~v.
Для элемента "жидкой линии"δ
~
` кинематическое уравнение движения :
dδ
~
`
dt
= ( δ
~
` · ∇)~v
по форме совпадает с уравнением движения вихря, поэтому для вихревой линии в про-
извольный момент времени
~ω = const · ρδ
~
`,
т.е.
ρ
0
da
p
ω
(0)
p
= ρ
dx
p
ω
p
или
ω
p
ω
(0)
p
=
Ã
ρ
0
ρ
!
e
p
≡ λ
3
e
p
. (6.134)
Здесь λ = (ρ
0
/ρ)
1/3
- коэффициент деформации потока. Для пульсационного движения
корреляционный тензор вихря Ω
ij
=< ω
i
ω
j
> можно выразить через корреляционную
функцию скоростей. В фурье - представлении
Ω
ij
= e
iαβ
e
jµν
K
α
K
µ
Φ
βν
. (6.135)
Используя выражение для
e
iαβ
e
jµν
= detkδ
r,s
k,
где (r = i, α, β; s = j, µ, ν), получаем:
Ω
ij
= −k
2
Φ
jl
+ (δ
ij
k
2
− k
i
k
j
)Φ
ll
. (6.136)
Записывая выражения (6.136) до и после деформации и учитывая, что из (6.134) следует
связь
Ω
ij
(~κ) = e
(i)
e
(j)
Ω
(0)
ij
(
~
k),
(~κ - волновой вектор пространства после деформации), можно найти изменение Ω
ij
при
деформации тензора Φ
ij
.
Будем предполагать, что в начальный момент турбулентность изотропна, так что спек-
тральный тензор имеет вид (6.49). Рассмотрим деформацию вдоль оси x
1
, так что
e
1
= c, e
2
= e
3
= λ
3/2
c
−1/2
(k
1
= cκ
1
, k
2
= λ
3/2
c
−1/2
κ
2
, k
3
= λ
3/2
c
−1/2
κ
3
).
При такой деформации
Φ
11
(κ) =
2π
2
E
0
(k)
λ
3
k
2
Ã
−c
2
k
2
− k
2
1
κ
2
+
κ
2
− κ
2
1
κ
4
"
c
3
(k
2
− k
2
1
) +
λ
3
6
(k
2
+ k
2
1
)
#!
, (6.137)
Φ
22
(κ) =
2π
2
E
0
(k)
λ
3
k
2
Ã
−
λ
3
cκ
2
(k
2
− k
2
2
) +
κ
2
− κ
2
2
κ
4
"
c
2
(k
2
− k
2
1
) +
λ
3
6
(k
2
+ k
2
1
)
#!
. (6.138)

6.5. НЕОДНОРОДНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 203
Выражение Φ
33
(χ) аналогично Φ
22
(χ). Среднее значения кинетической энергии вдоль
оси p определяется интегралом Φ
pp
(χ), а относительное изменение продольной и попе-
речной к оси деформации потока равны по определению
µ
allel
=
< (v
0
)
2
1
>
< (v
0
)
2
10
>
=
R
Φ
11
d
3
κ
R
Φ
(0)
11
d
3
κ
, (6.139)
µ
⊥
=
< (v
0
)
2
2
>
< (v
0
)
2
20
>
=
R
Φ
22
d
3
κ
R
Φ
(0)
22
d
3
κ
, (6.140)
В результате подстановки (6.137) и (6.138) получим:
µ
allel
λ
2
=
3
4c
2
"
1 + α
2
2α
3
ln
1 + α
1 − α
−
1
α
2
#
, (c > 1);
µ
⊥
λ
2
=
3c
4
+
3
4c
2
Ã
1
2α
2
−
1 − α
2
4α
3
ln
1 + α
1 − α
!
, (c > 1);
µ
allel
λ
2
=
3
4c
2
Ã
1
α
2
+
α
2
− 1
α
3
arctan α
!
, (c < 1);
µ
⊥
λ
2
=
3c
4
+
3
4c
2
Ã
1 + α
2
2α
3
arctan α −
1
2α
2
!
, (c < 1).
Здесь α = 1 − c
−3
. Эти результаты можно применить к описанию изменения характе-
ристик турбулентности в сопле. Величина деформации при этом λ
3
/c пропорциональна
площади поперечного сечения сопла, а из уравнения непрерывности ρuF = const тогда
следует c ∼ u.
Задача 3. Найти изменения продольного и поперечного масштабов турбу-
лентности при быстрой осессиметричной деформации потока.
Решение. Выберем две точки, находящиеся на расстоянии r = x
1
− ˜x
1
в потоке.
Используем определения масштабов турбулентности (6.116) и выполним преобразование
Фурье:
`
allel
=
1
< (v
0
1
)
2
>
Z
∞
−∞
< v
0
1
˜
v
0
1
> dr
1
=
1
< (v
0
1
)
2
>
Z
∞
r
1
=−∞
dr
1
Z
Φ
11
(~κ)e
iκ
1
r
1
d
3
κ, (6.141)
`
⊥
=
1
< (v
0
2
)
2
>
Z
∞
−∞
< v
0
2
˜
v
0
2
> dr
2
=
1
< (v
0
2
)
2
>
Z
∞
r
2
=−∞
dr
2
Z
Φ
22
(~κ)e
iκ
2
r
2
d
3
κ, (6.142)
Подставляя сюда решения (задача 2) для спектрального тензора при быстрой деформа-
ции, получим
`
allel
`
allel
(0)
=
1
µ
allel
c
,
`
⊥
`
⊥
(0)
=
c
1/2
µ
⊥
λ
3/2
.
,
Задача 4. Определить изменение характеристик турбулентности при про-
хождении турбулентного потока через перпендикулярно расположенную сет-
ку, считая, что изменение распределения скоростей обусловлено сопротивле-
нием (падением давления),т.е. является безвихревым. Считать заданными
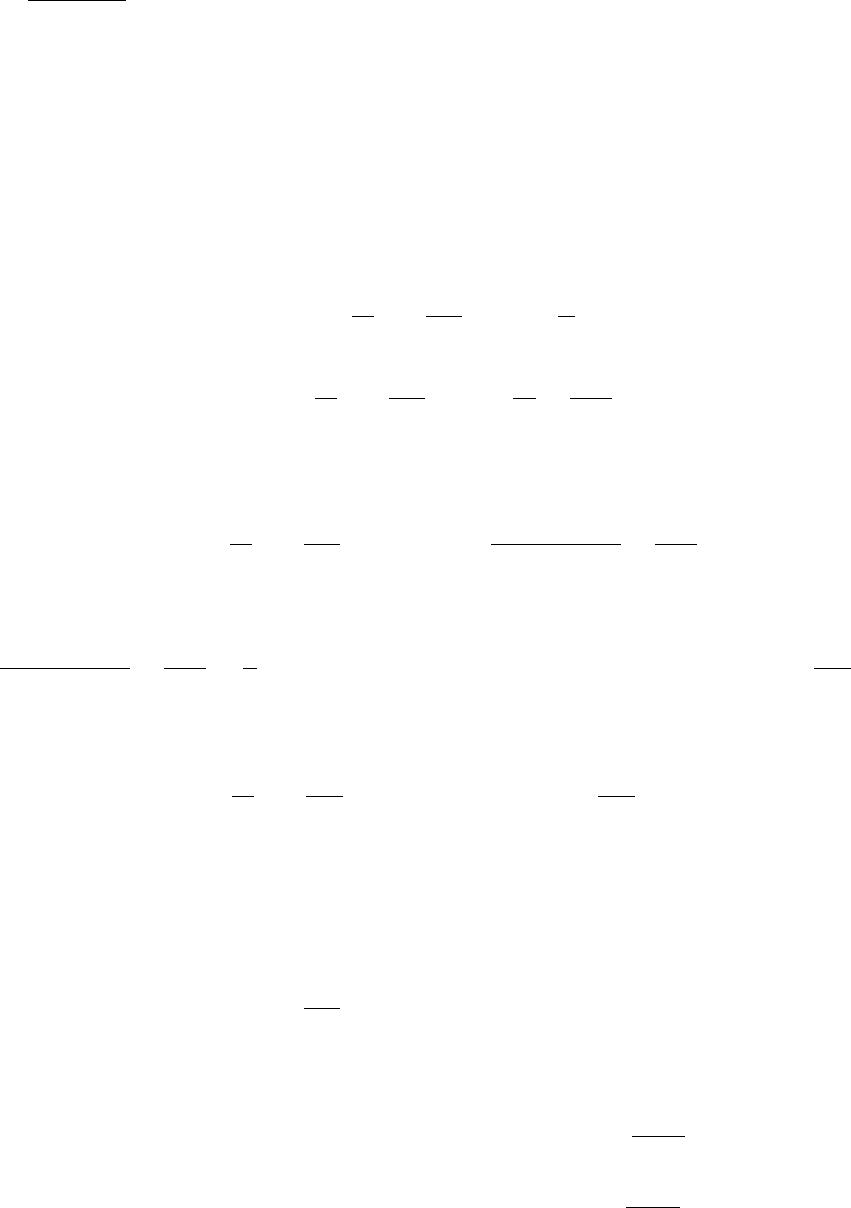
204 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ
коэффициент сопротивления сетки λ и коэффициент поворота поперечной
пульсационной скорости (Дж.К.Бэтчелор [33]).
Решение. Обозначим параметры турбулентного потока перед сеткой p
0
, v
0
i
, за сеткой
p”, v”
i
. Здесь v
0
i
, v”
i
- вихревые турбулентные поля скоростей далеко от сетки. Сетка
вносит дополнительное влияние, создавая пульсационные скорости ∇ϕ
0
, ∇ϕ” (ϕ
0
, ϕ” -
потенциалы безвихревых составляющих). Найдем связи между пульсационными скоро-
стями при переходе через сетку. Для суммарных пульсационных скоростей у сетки
v”
2
(0) = αv
0
2
(0), v”
3
(0) = αv
0
3
(0), v”
1
(0) = v
0
1
(0). (6.143)
Ось x
1
направлена вдоль потока перпендикулярно сетке, аргумент "0"в (6.143) означает
x
1
= 0. Найдем связь между безвихревыми составляющими. Уравнения движения для
потенциалов ϕ
0
и ϕ” имеют вид:
Ã
∂
∂t
+ U
∂
∂x
1
!
ϕ
0
= −
p
0
ρ
,
Ã
∂
∂t
+ U
∂
∂x
1
!
ϕ − −
p”
ρ
+
βU
2
2
.
Здесь член βρU
2
/2 описывает уменьшение давления за сеткой вследствие сопротивления
и определяет уровень давления при x
1
→ ∞. Вычитая эти уравнения, получим:
Ã
∂
∂t
+ U
∂
∂x
1
!
(ϕϕ
0
)
x
1
=0
=
p
0
(0) − p”(0)
ρ
−
βU
2
2
.
Правая часть уравнения может быть преобразована следующим образом:
p
0
(0) − p”(0)
ρ
−
βU
2
2
=
β
2
h
(U + u
1
)
2
+ u
2
2
+ u
2
3
− U
2
i
= βUu
1
(−0) = βU
Ã
u
0
1
+
∂ϕ
0
∂x
1
!
x
1
=0
.
В результате получим уравнение:
Ã
∂
∂t
+ U
∂
∂x
1
!
(ϕϕ
0
)
x
1
=0
= βU
Ã
u
0
1
+
∂ϕ
0
∂x
1
!
x
1
=0
. (6.144)
Найдем закон убывания ϕ
0
, ϕ” при удалении от стенки. Из уравнения непрерывности
следует, что потенциал является гармонической функцией (∆ ϕ = 0). Координаты x
2
, x
3
и время t является однородными координатами, поэтому по ним можно применить пре-
образование Фурье. Уравнение ∆ϕ = 0 тогда имеет вид:
Ã
∂
2
∂x
2
1
− k
2
⊥
!
˜ϕ = 0, k
2
⊥
= k
2
2
+ k
2
3
. (6.145)
Из уравнения (6.145) следует, что ϕ
0
и ϕ” экспоненциально уменьшаются при удалении
от сетки:
ϕ
0
(~x, t) =
Z
e
−ik
1
Ut+ik
2
x
2
+ik
3
x
3
+k
⊥
x
1
˜ϕ
0
(
~
k)
d
3
k
(2π)
3
, (6.146)
ϕ(~x, t) =
Z
e
−ik
1
Ut+ik
2
x
2
+ik
3
x
3
+k
⊥
x
1
˜ϕ(
~
k)
d
3
k
(2π)
3
, (6.147)

6.6. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 205
Подставляя эти уравнения в (6.144) получим:
(−ik
1
− k
⊥
) ˜ϕ(−ik
1
+ k
⊥
) ˜ϕ
0
= β(˜u
0
1
+ k
⊥
˜ϕ
0
). (6.148)
Подставляя сумму вихревых и безвихревых пульсационных скоростей в ( 6.143), полу-
чим:
˜v
p
” + ik
p
˜ϕ − α(˜u
0
p
+ ik
p
˜ϕ
0
), (p = 2, 3); (6.149)
˜v”
1
− k
⊥
˜ϕ − ˜v
0
1
+ k
⊥
˜ϕ
0
. (6.150)
Из уравнения непрерывности следует
~
k · ~v
0
=
~
k · ~v − 0. Соотношения (6.148), (6.149)
позволяют связать преобразования Фурье пульсационной скорости до и после решетки:
˜v”
i
= α˜v
0
i
(
~
k) +
k
2
δ
1i
− k
1
k
i
k
2
⊥
[J(γ) − α]˜v
0
1
(k). (6.151)
Здесь γ = k
1
/k
⊥
,
J(γ) =
(γ + i)[2αγ + i(αβ − 1 − α)]
(γ − i)[2γ + i(β + α + 1)]
, (6.152)
Из (6.151) можно получить связь между продольными и поперечными компонентами
спектрального тензора:
Φ”
allel
(k) = |J|
2
Φ
0
allel
(k),
Φ”
22
+ Φ”
33
= α
2
(Φ
0
22
+ Φ
0
11
) + γ
2
(|J|
2
− α
2
)Φ
0
11
.
Относительные уменьшения продольной и поперечной пульсационных энергий равны:
f
allel
=
< (v”)
2
1
>
< v
2
j
>
=
R
|J|
2
Φ
0
11
(k)d
3
k
R
Φ
0
11
(k)d
3
k
,
f
⊥
=
< (v”)
2
2
> + < (v”)
2
3
>
< (v
0
)
2
2
> + < (v
0
)
2
3
>
= α
2
+
R
γ
2
|J|
2
− α
2
)Φ
0
11
(k)d
3
k
R
(Φ
0
22
+ Φ
0
33
)d
3
k
.
Если турбулентность перед сеткой изотропна, то подставляя для Φ
0
ij
(k) (6.49), получим:
f
allel
=
R
∞
−∞
(1 + γ
2
)
−3/2
|J|
2
dγ
R
∞
−∞
(1 + γ
2
)
−3/2
dγ
,
f
⊥
= α
2
+
1
3
(αβ − 1 − α)
2
−
1
3
f
allel
(α + β + 1)
2
.
Параметры α и β обычно не являются независимыми, так в [33] рассматривается следую-
щая связь между ними: α ≈ 1, 1(1+β)
−1/2
. Тогда единственным параметром, характери-
зующим сетку, является коэффициент сопротивления β, с ростом которого уменьшаются
f
allel
и f
⊥
.
6.6 Взаимодействие электромагнитного поля с турбулентным дви-
жением электропроводных сред
В настоящем параграфе рассматривается турбулентное движение проводящей сплош-
ной среды в отличие от турбулентности разреженной плазмы, которая рассматривается,
206 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ
например, в [39], [40]. При этом будем ограничиваться не слишком большими значени-
ями магнитных полей, при которых коэффициенты переноса (электро-и теплопровод-
ность) являются изотропными, что соответствует малым значениям параметра Холла.
В таких условиях турбулентное движение среды имеет много общих черт с турбулент-
ным движением газа, а коллективные неустойчивости и связанные с ними механизмы
турбулентного движения разреженной плазмы не проявляются. Экспериментальных ис-
следований по турбулентности электропроводных сред в настоящее время недостаточно
даже для построения полуэмпирической теории, аналогичной рассмотренной в разде-
ле 6.6 для неэлектропроводных газов и жидкостей. Основная часть опытных данных
получена в турбулентности жидких металлов, поэтому перенос результатов на движе-
ние высокотемпературной сред вызывает затруднения и в данном разделе рассмотрение
ограничивается только таким кругом вопросов, в которых почти не проявляется каче-
ственное различие между плазмой и жидкими металлами.
Будем рассматривать движение проводящей среды в условиях, когда справедливо
магнитогидродинамическое приближение [49], при котором все действие электромагнит-
ных полей можно свести к действию дополнительной электромагнитной силы в урав-
нении движения и джоулева тепловыделения в уравнении энергии. Эти члены опреде-
ляются действием внешних и индуцированных при движении среды электромагнитных
полей, величина которых определяется из уравнения магнитной индукции. В указанном
приближении система уравнений, описывающая движение среды имеет вид [49]:
∂ρ/∂t + ∂ρv
k
/∂x
k
= 0; (6.153)
ρ
∂v
i
∂t
+ ρv
k
∂v
i
∂x
k
= −
∂ρ
∂x
i
+
∂τ
ik
∂x
k
+
H
k
4π
µ
∂H
i
∂x
k
−
∂H
k
∂x
i
¶
; (6.154)
ρ
∂h
∂t
+ ρv
k
∂h
∂x
k
=
∂ρ
∂t
+ v
k
∂ρ
∂x
k
+ τ
ik
∂v
i
∂x
k
−
∂(q + q
R
k
)
∂x
k
+
+
ν
m
8π
µ
∂H
i
∂x
k
−
∂H
k
∂x
i
¶µ
∂H
i
∂x
k
−
∂H
k
∂x
i
¶
; (6.155)
∂H
i
∂t
+ v
k
∂H
i
∂x
k
= H
k
∂v
i
∂x
k
− H
i
∂v
k
∂x
k
+ ν
m
∂
2
H
i
∂x
2
k
+
∂ν
m
∂x
k
µ
∂H
i
∂x
k
−
∂H
k
∂x
i
¶
; (6.156)
∂H
k
/∂x
k
= 0 . (6.157)
Здесь ν
m
= c
2
/4πσ - коэффициент магнитной вязкости, τ
ik
- тензор вязких напряжений.
Уравнения магнитной гидродинамики (6.153-6.157) описывают квазинейтральную плаз-
му и могут нарушаться вблизи стенок, на расстояниях порядка дебаевского радиуса, где
существует нескомпенсированный объемный заряд и значительные изменения потенци-
ала. Для того, чтобы избежать осложнений, связанных с такими слоями, в некоторых
случаях можно переформулировать граничные условия, поставив их на воображаемой
поверхности, удаленной от истинной на малое расстояние. В дальнейшем будем предпо-
лагать справедливыми уравнения магнитной гидродинамики вплоть до стенок. В маг-
нитной гидродинамике наряду с обычными безразмерными параметрами появляются
два новых, один из которых - магнитное число Рейнольдса Re
m
определяет воздействие
потока на магнитное поле, т.е. величину индуцированного магнитного поля, а второй -
действие магнитного поля на поток (число Стюарта или Гартмана). Рассмотрим вна-
чале случай Re
m
>> 1, когда среда является идеально проводящей и магнитное поле

6.6. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 207
"вморожено"в плазму, т.е. каждая силовая линия все время проходит через одни и те
же частицы среды. Для больших значений магнитного числа Рейнольдса турбулент-
ных пульсаций (Re
M
= ω`/ν
m
>> 1) представление о "вмороженном"магнитном поле
применимо при рассмотрении движения крупных турбулентных вихрей, а также при
исследовании мелкомасштабной структуры турбулентности в таком диапазоне масшта-
бов, для которого Re
m
>> 1. Это означает, что магнитные силовые линии получаются
столь же запутанными, как и линии движения жидких частиц, т.е. возникает турбулент-
ное магнитное поле. Физической причиной его возникновения и поддержания являются
турбулентные электрические токи, возникающие в среде при турбулентных пульсациях
скорости при наличии магнитного поля и пульсациях самого поля. В пульсационном
магнитном поле может содержаться значительная часть общей энергии турбулентно-
сти. Рассмотрим теперь случай Re
m
¿ 1. Из уравнения магнитной индукции (6.157)
следует, что величина индуцированного магнитного поля H
0
/H ∼ Re
m
¿ 1, поэтому
удобно представить магнитное поле в среде в виде суммы внешнего и индуцированного
H + H
0
. Считая внешнее поле Н стационарным и создающимся током, не протекающим
в области течения, так что rot
~
H = (4π/C)j
bH
= 0 , из (6.156) получим:
∂H
0
i
∂t
+ v
k
∂H
i
∂x
k
+ v
k
∂H
0
i
∂x
k
= H
k
∂v
i
∂x
k
− H
i
∂v
k
∂x
k
+ H
0
k
∂v
i
∂x
k
− H
0
i
∂v
k
∂x
k
+
+ν
m
∂
2
H
0
i
∂x
k
∂x
k
+
∂ν
m
∂x
k
µ
∂H
0
i
∂x
k
−
∂H
0
k
∂x
i
¶
. (6.158)
При исследовании турбулентного движения проводящей среды наиболее важен случай,
когда индуцированное машинное поле
~
H вызывается электрическими токами, возникаю-
щими в среде при ее движении во внешнем магнитном поле. Величина индуцированных
движением среды электрических токов и, следовательно, величина
~
H может ограни-
чиваться либо омическим, либо индуктивным сопротивлением среды. В первом случае
из (6.158) следует оценка ν
m
H
0
/L
2
∼ Hv/L, т.е. H
0
/H ∼ Re
m
¿ 1. Члены v
k
(∂H
0
i
/∂x
k
)
и H
0
k
(∂v
`
/∂x
j
) по отношению к члену ν
m
(∂
2
H
0
/∂x
2
) имеют порядок Re
m
¿ 1, т.е. ими
можно пренебречь. Оценим величину члена ∂H
0
i
/∂t ∼ H
0
/τ, который описывает "ин-
дуктивное сопротивление"плазмы. Величина времени изменения пульсационного поля
~
H определяется характерным временем изменения скорости v. Это время следует оце-
нивать из уравнения движения, приравнивая ускорение жидкой частицы v/τ и раз-
личным удельным силам, вызывающим ее движение. При действии инерционных сил
τ = τ
um
∼ L/v, при действии магнитного поля τ = τ
H
∼ 4πLρv/Hh, при существенном
действии градиента давления τ ∼ τ
ρ
. Если перепад давления определяется движением
среды со скоростью v, то ∆ρ ∼ ρv
2
и из уравнения движения следует τ
ρ1
∼ τ
uH
∼ L/v,
если ∆ρ уравновешивается электромагнитными силами, то τ
ρ2
∼ τ
H
, если ∆ρ опре-
деляется акустическими колебаниями в среде, то ∆ρ ∼ ρv
ak
α,где α - скорость звука,
v
ak
- характерная величина скорости смещения среды при акустических колебаниях. В
неподвижной среде v
ak
= v и τ
ρs
∼ L/α, в турбулентной среде v
ak
можно оценить из
уравнения неразрывности (1/ρ)(dρ/dt) = −∂v
k
/∂x
k
, откуда следует ρ
0
/ρτ ∼ v
CH
/L (τ -
характерное время изменения плотности, v
CH
- скорость смещения среды); подставляя
сюда связь ρ
0
и p
0
в акустических колебаниях ρ
0
= ρ
0
/a
2
, получаем v
CH
∼ Lp
0
/ρa
2
τ. В
турбулентном потоке p
0
, τ определяются турбулентными пульсациями p
0
∼ ρw
2
, τ ∼ `/w,
учитывая, что v
ak
< v
CH
, т.к. не все смещения среды, происходящие при пульсациях
плотности приводят к генерации звуковых волн, получим v
ak
/w < (w/a)
2
. Таким обра-

208 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ
зом, в турбулентной среде, когда изменение индуцированного магнитного поля опреде-
ляется пульсациями давления, τ
p4
∼ Lw/av
ak
∼ La/w
2
. Если магнитное поле достаточно
большое, пульсации давления вызываются электромагнитными силами и p
0
∼ HH
0
/4π,
в этом случае v
CM
∼ Lp
0
/ρa
2
τ
H
и τ
p3
∼ (L/a )(w/v
ak
), где
v
ak
w
<
LH
2
Re
m
4πρa
2
·
H
2
Re
m
4P Lρw
2
=
µ
C
A
α
¶
2
µ
C
A
L
ν
m
¶
2
,
где C
A
= H/
√
4πρ - альфвеновская скорость колебаний в среде. Подставляя τ
p1
, ..., τ
p5
в условие, определяющее малость индуцированного магнитного поля (L
2
/ν
m
τ
p
¿ 1),
получим следующие неравенства:
L
2
ν
m
τ
1
=
Lv
ν
m
= Re
m
¿ 1; (6.159)
L
2
ν
m
τ
2
=
µ
LC
A
ν
m
¶
2
¿ 1; (6.160)
L
2
ν
m
τ
3
=
αL
ν
m
= Re
m
(α) ¿ 1; (6.161)
L
2
ν
m
τ
4
=
Lw
ν
m
w
α
= Re
m
(w) ·
w
α
¿ 1; (6.162)
L
2
ν
m
τ
5
=
Lα
ν
m
µ
C
A
α
¶
2
µ
C
A
L
ν
m
¶
2
=
C
A
α
µ
C
A
L
ν
m
¶
3
¿ 1. (6.163)
Все эти условия обычно выполняются. Физический смысл неравенств заключается в сле-
дующем: при Re
m
¿ 1 справедливо приближение линейной магнитной гидродинамики,
т.е. можно учитывать влияние на поток только внешнего магнитного поля и вызывае-
мых им токов. При выполнении условия (6.160) оказывается несущественной генерация
магнитогидродинамических волн турбулентными пульсациями. При выполнении усло-
вия (6.163) динамика развития турбулентности может рассматриваться без учета гене-
рации акустических колебаний. Безиндукционное приближение (малость члена ∂H
0
/∂t)
означает, что магнитное поле
~
H в каждый момент времени определяется полями гидро-
динамических параметров в этот же момент времени, т.е. квазистационарно "следит"за
величинами этих параметров. Рассмотрим качественно воздействие магнитного поля на
турбулентное
движение проводящей среды. Если течение является плоским, а внешнее магнитное
поле постоянно и перпендикулярно плоскости течения, то его действие на поле скоро-
стей проявляется только в том случае, если div~v 6= 0, т.е. на движение несжимаемой
жидкости магнитное поле никакого влияния не оказывает. Приведем доказательство
этого утверждения: при div~v = 0 и плоском движении жидкости площадь, охватыва-
емая любой замкнутой линией, лежащей в плоскости течения и движущейся вместе с
жидкостью, не изменяется с течением времени, поэтому сохраняется магнитный поток
через этот контур и не возникает индукционных токов и электромагнитных сил. Если
div~v 6= 0, то при плоском движении среды в постоянном магнитном поле, перпенди-
кулярном плоскости течения, в среде возникают такие электрические токи, взаимодей-
ствие которых с магнитным полем приводит к появлению сил, препятствующих расши-
рению или сжатию среды (т.е. сил, действие которых направлено на уменьшение | div~v |).
Следовательно, если бы при плоском среднем движении жидкости в перпендикулярном
6.6. ВЗАИМОДЕЙСТВИЕ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 209
плоскости течения постоянным магнитном поле существовала чисто плоская турбулент-
ность, то магнитное поле не оказывало бы никакого действия на это движение. Если при
плоском среднем движении жидкости турбулентность является трехмерной, то в жид-
кости появятся такие электромагнитные силы, которые будут стремиться уменьшить
| ∂v
0
1
/∂x
1
+ ∂v
0
2
/∂x
2
|= −∂v
0
3
/∂x
3
, т.е. увеличить размер турбулентных вихрей по оси x
3
.
Эти же рассуждения применимы и к осесимметричному случаю, если среднее движение
жидкости происходит в меридиональных плоскостях, а магнитное поле создается элек-
трическим током, протекающим вдоль оси симметрии. Аналогичные особенности имеет
и турбулентность в продольном магнитном поле, т.е. когда магнитное поле направле-
но параллельно средней скорости. При этом также происходит увеличение масштаба
вихрей вдоль поля, но турбулентность не становится плоской, как в поперечном поле
[36]. Степень влияния продольного магнитного поля на турбулентность высокотемпера-
турных сред зависит от температуры, поэтому в пограничном слое на холодной стенке
может сложиться такая необычная ситуация, когда течение в верхней части погранич-
ного слоя будет ламинарным, из-за подавления турбулентности магнитным полем, а у
стенки - турбулентным.
6.6.1 Однородная магнитогидродинамическая турбулентность
Наиболее простым случаем турбулентности в несжимаемой жидкости в отсутствие элек-
тромагнитных полей является однородная изотропная турбулентность, рассмотренная
в 6.4. В магнитном поле турбулентность не может быть изотропной из-за наличия вы-
деленного направления, связанного с магнитным полем, но может быть однородной.
Такая однородная магнитогидродинамическая турбулентность имеет практическое при-
ложение для течений электропроводных сред за турбулизирующими решетками, и, без-
условно, эта задача важна для построения полуэмпирической теории турбулентности в
магнитном поле. В задачах однородной турбулентности удобно использовать спектраль-
ную форму уравнений. Вывод уравнения для спектральной функции корреляции скоро-
стей Φ
ij
(6.170) аналогичен выводу уравнения (6.50). Система уравнений, описывающая
движение несжимаемой жидкости в магнитном поле в безиндукционном приближении
имеет вид (для точек M(~x)
˜
M(
~
˜x)):
∂v
i
∂t
+
∂
∂x
`
v
i
v
`
= −
1
ρ
∂p
∂x
i
+ ν
∂
2
v
i
∂x
`
∂x
`
+
H
`
4πρ
∂H
0
i
∂x
`
, (6.164)
∂ ˜v
j
∂t
+
∂
∂x
`
˜v
i
˜v
`
= −
1
ρ
∂p
∂x
j
+ ν
∂
2
˜v
j
∂x
`
∂x
`
+
He
4πρ
∂
˜
H
0
j
∂x
`
. (6.165)
Здесь p = p
ra3
+
~
H ·
~
H
0
/4π. К уравнениям движения ( 6.164, 6.165) следует добавить
уравнения несжимаемости жидкости ∂v
i
/∂x
i
= 0 и соленоидеальности магнитного поля
∂H
0
i
/∂x
i
= 0 , а также уравнения магнитной индукции
ν
m
∂
2
H
0
i
∂x
2
`
+ He
∂v
i
∂x
`
= 0 , (6.166)
ν
m
∂
2
˜
H
0
j
∂˜x
2
`
+ He
∂˜v
j
∂x
`
= 0. (6.167)
Как и при выводе (6.50) умножим (6.164) на ˜v
j
, (6.165) на v
i
, сложим полученные урав-
нения и осредним их, затем перейдем к однородной координате r
`
= ˜x
`
−x
`
и применим

210 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ
фурье-преобразование на этой координате. Получающиеся корреляционные функции
давления и скоростей hp˜v
j
i и h˜pv
i
i исключим, как и в 6.40. Для исключения корреля-
ционных функций hH
0
i
˜v
j
i и h
˜
H
0
j
v
i
i используем уравнения (6.166) и (6.167), умножая
их на ˜v
j
и v
i
соответственно, осредняя, переходя к однородной координате и выполняя
преобразование Фурье. В результате получим уравнение
∂Φ
ij
∂t
= A
ij
(
~
k) + B
ij
(
~
k) − 2νk
2
Φ
ij
− ν
m
cos
2
ϕΦ
ij
, (6.168)
ψ
M
= 2C
2
A
/ν
m
, ϕ - угол между волновым вектором
~
k и магнитным полем
~
H. Тен-
зоры A
ij
, B
ij
определяются равенствами (6.51, 6.52) с соответствующими свойствами
(6.57, 6.59), откуда следует их физический смысл - A
ij
ответственен за перераспределе-
ние энергии от крупных вихрей к малым, а B
ij
приводит к перераспределению энергии
пульсаций по различным осям координат. Проанализируем влияние магнитного поля на
однородную турбулентность. Для этого рассмотрим частные случаи уравнения (6.168).
I.A
ij
≈ B
ij
≈ 0 . Это возможно в двух случаях. В первом - при малых числах Рейнольдса
Re = w`/ν ¿ 1, когда все тройные корреляции малы, что соответствует вырождению
турбулентности. Во втором, когда влияние магнитного поля настолько велико, что пре-
вышает действие процессов, описывающихся членами A
ij
, B
ij
, отношение этих членов
определяется параметром
ξ
M
=
`H
2
2πρν
m
w
=
2
Re
m
µ
`C
A
ν
m
¶
2
.
При ξ
M
>> 1 членами A
ij
и B
ij
можно пренебречь для всех углов ϕ не близких к π/2.
Если вначале турбулентность была изотропной, то вследствие быстрого угасания вих-
рей, имеющих ϕ ≈ π/2, турбулентность станет анизотропной и члены с A
ij
, B
ij
станут
существенными. Следовательно, решение с A
ij
= B
ij
= 0 в этом случае будет справед-
ливо только на ограниченном интервале времени. Найдем решение уравнения (6.168)
при A
ij
= B
ij
= 0:
Φ
ij
(
~
k) = Φ
(0)
ij
(
~
k)exp
·
−(ψ
H
cos
2
ϕ + 2νk
2
)t
¸
. (6.169)
Если турбулентность в начальный момент времени была изотропной, то Φ
(0)
ij
(
~
k) опре-
деляется формулой (6.49). Найдем значения продольных и поперечных пульсационных
скоростей:
w
2
11
= hv
0
2
1
i =
Z
Φ
11
(
~
k, r)
d
3
k
(2π)
3
=
Z
∞
0
E(k)e
−2νk
2
t
dk
Z
1
0
(1 − µ
2
)e
−ψ
H
µ
2
t
dµ, (6.170)
w
2
⊥
= hv
0
2
1
i =
Z
Φ
22
(
~
k, t)
d
3
k
(2π)
3
=
Z
∞
0
E(k)e
−2νk
2
t
dk
Z
1
0
1 + µ
2
2
e
−ψ
H
µ
2
t
dµ. (6.171)
Первый интеграл можно вычислить для больших чисел Re = w`/ν, когда можно считать
exp(−2νk
2
t) ≈ 1, что справедливо при 2νk
2
t ¿⊥ или t ¿ Re`
0
/2w
0
, тогда
Z
∞
0
E(k)exp(−2νk
2
t)dk ≈ 3w
2
0
/2, (6.172)
w = w
110
= w
⊥
0 - начальная пульсационная скорость.Для относительной пульсационной
энергии получим
f
11
= w
2
11
/w
2
0
≈
3
2
Z
1
0
(1 − µ
2
) exp(−ψ
H
tµ
2
)dµ,
