Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

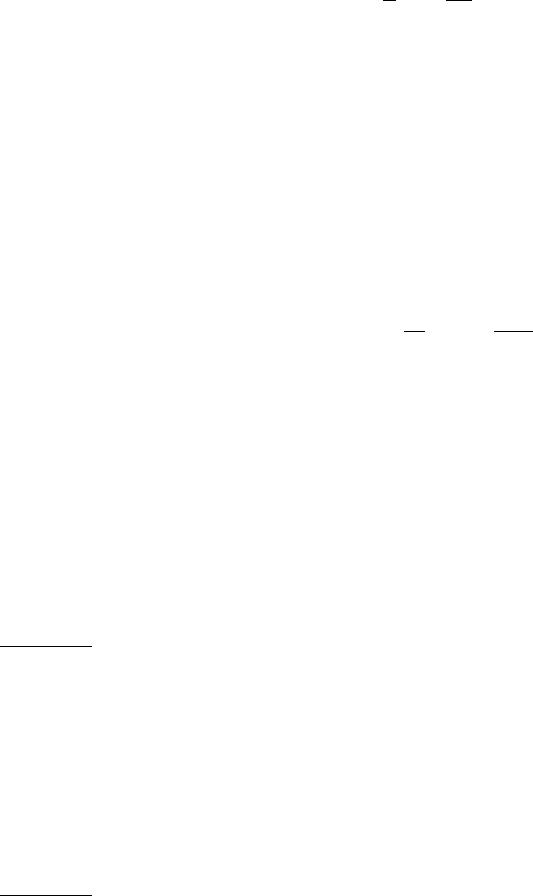
6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 181

в нем происходит вязкая диссипация вихрей, т.е. переход кинетической энергии турбу-

лентного движения в тепловую энергию, что описывается последним членом в уравне-

нии (6.50). В соответствии с представлениями о механизме каскадной передачи энергии

от крупных вихрей к мелким, член T (k) должен быть отрицательным в энергетическом

интервале и положительным в вязком, его интеграл по спектру равен нулю в соответ-

ствии с (6.60).

Из соотношения между масштабами турбулентности (6.9) следует, что при боль-

ших числах Re существует большой инерционный интервал, определяемый условиями

−1

¿ k ¿ r

−1

. Теорию локально-изотропной турбулентности А.Н.Колмогорова можно

применить и к спектральным функциям. Любой момент в спектральной форме имеет

вид

= [ M

1/3

kν

= [M

]ϕ(kr

), (6.62)

где величина (ε/k)

1/3

имеет размерность скорости, [M

] - размерность величины M

выраженная через характерные скорость v

= (εν)

1/4

и расстояние r

= ν

3/4

/ε

1/4

. В

инерционном интервале момент (6.62) не зависит от вязкости, аргументами функций

являются только v

= (ε/k)

1/3

и k. Рассмотрим, например, спектральную плотность

энергии, размерность которой устанавливается из формулы (6.48):

E(k) = v

ϕ(kr

). (6.63)

В инерционном интервале получаем

E(k) =

= A

2/3

5/3

, (6.64)

где A

≈ 0, 92. Зависимость E(k) ∼ k

−5/3

носит название "закона 5/3"Колмогорова-

Обухова. Аналогично могут быть получены спектральные зависимости и других корре-

ляционных функций в инерционном интервале.

6.4.4 Задачи

Задача 1. Показать, что для однородной изотропной турбулентности кор-

реляционная функция скоростей удовлетворяет неравенству B

(r) ≤ B

(0).

(Дж.К.Бетчелор [33])

Решение. Из формулы (6.28) следует

2 (B

(0) − B

(r)) = R

(r) =< (∆v

)

>≥ 0,

или

(r) ≤ B

(0).

Задача 2. Доказать связи (6.5) между продольными и поперечными кор-

реляционными функциями скоростей в инерционном интервале для однород-

ной изотропной турбулентности.

Решение. В этом случае продольная и поперечная корреляционные функции выра-

жаются формулами (6.2) (см. задачу 1):

≡< (∆v

)

>= A

(εr)

2/3

, R

≡< (∆v

)

>= A

(εr)

2/3

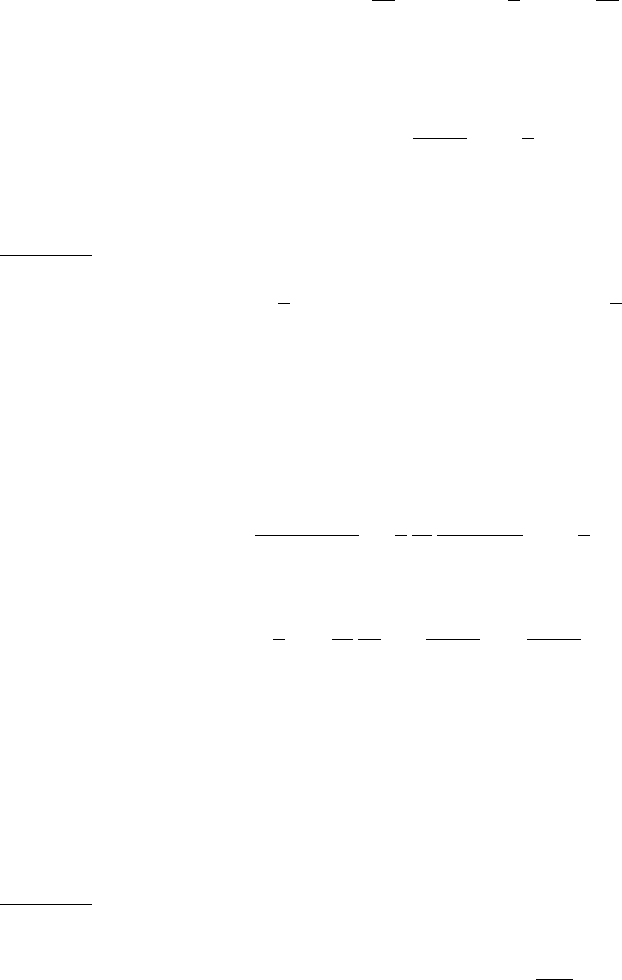
182 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Подставляя эти выражения в уравнение, аналогичное (6.25), для R

получаем A

/3. Для корреляций третьего порядка:

LLL

≡< (∆v

)

>=< (v

− ˜v

)

>= 3(< v

˜v

> − < v

˜v

>) = A

εr,

LNN

≡< ∆v

(∆v

)

>=< (v

− ˜v

)(v

˜v

)

>= A

εr.

Значения этих моментов выражаются через тройные корреляционные функции:

LLL

= 3(B

LL,L

− B

L,LL

) = 6B

LL,L

LNN

= B

L,NN

− B

NNL

+ 2(B

N,LN

− B

NL,N

) = − 2B

NN,L

− 4B

NL,L

LNN

= −B

LL,L

− r

LL,L

= −

1 + r

LLL

откуда следует A

= −A

/3.

Задача 3. Получить соотношение Колмогорова

LLL

− 6ν

= −

rε

и показать, что в инерционном интервале из него следует A

= −4/5, A

= 4/15

в формулах (6.3).

Решение. Подставим в правую часть уравнения Кармана-Ховарта (6.38) выражения

(r, t) = −

(r, t) + B

(0, t), B

LL,L

LLL

(r, t)

(см. задачи 1, 2). Рассмотрим это уравнение в области r ¿ L , где L - интегральный мас-

штаб турбулентности. В этой области турбулентность является локально изотропной,

т.е. корреляционные функции R

, R

LLL

определяются только значениями вязкости и

диссипации (ν и ε) и не зависят явно от времени. Уравнение Кармана-Ховарта при этом

зависит только от координат, т.к. скорость убыли кинетической энергии определяется

диссипацией:

∂B

(0, t)

∂t

< v

= −

ε.

Подставляя в уравнение Кармана-Ховарта:

−

ε =

LLL

− ν

умножая на r

и интегрируя от нуля до r , получаем искомое соотношение Колмогорова.

В инерционном интервале в этом соотношении можно пренебречь членом с вязкостью,

тогда получим R

LLL

= −(4/5)rε , следовательно, A

= −4/5 , а из связи A

и A

находим

= −A

/3 = 4/15 .

Задача 4. Показать, что корреляционные функции скоростей однородной

изотропной турбулентности в несжимаемой среде в вязком интервале имеют

вид R

= εr

/15ν, R

= 2 εr

/15ν (А.Н.Колмогоров [45]).

Решение. В вязком интервале изменения скорости малы из-за действия сил вязкости,

поэтому их можно разложить в ряды Тейлора:

∆v

= v

(r) − v

(0) = r

∂v

∂r

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 183

∆v

= v

(r) − v

(0) = r

∂v

∂r

Продольная и поперечная корреляционные функции равны:

=< (∆v

)

>= r

*Ã

∂v

∂r

= Ar

=< (∆v

)

>= r

*Ã

∂v

∂r

= A

Используя связь между продольной и поперечной корреляционными функциями (6.25),

(6.29), получаем A

= 2A. В вязком интервале константу A можно выразить через вяз-

кость и диссипацию энергии:

ε =

*Ã

∂v

∂x

∂v

∂x

!Ã

∂v

∂x

∂v

∂x

. (6.65)

Для этого выразим (6.65) через R

. В (6.65) содержатся члены двух типов:

∂v

∂x

∂v

∂x

∂

∂x

∂v

∂x

−

∂

∂x

∂

∂x

(x)v

(x)i = 0 .

Здесь использовано уравнение неразрывности и условие однородности турбулент-

ности

< v

(x)v

(x) >= h v

(0)v

(0)i = const.

∂v

∂x

∂v

∂x

∂

∂x

∂v

∂x

−

∂

∂x

∂

∂x

< v

(x) > −

∂

∂x

= −

∂

∂x

Используя эти преобразования в (6.65), получаем

= −

∂

∂x

Сравнивая с определением (6.23), находим:

= −

∂

r=0

∂

∂r

. (6.66)

Учитывая, что R

= R

+ 2R

= 5 Ar

, получаем A = ε/15ν.

Задача 5. Найти асимптотическое поведение корреляционной функции

скоростей и кинетической энергии турбулентности на стадии распада, ко-

гда можно пренебречь тройными корреляциями скоростей. (А.С.Монин,

А.М.Яглом [32]).

184 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Решение. Переходя к сферическим переменным в 5-мерном пространстве и интегри-

руя по угловым переменным в (6.40), получаем:

(r, t) =

4νtr

3/2

∞

, 0)(r

)

5/2

3/2

4νt

exp

−

+ (r

)

8νt

В пределе t → ∞, заменяя модифицированную функцию Бесселя I

3/2

(x) ее первым

членом при x → 0, находим

(r, t) ≈

√

2π(νt)

5/2

exp

−

8νt

. (6.67)

Здесь Λ - инвариант Лойцянского. Кинетическая энергия турбулентности убывает по

закону

< u

>= R

(0, t) =

√

2π(νt)

5/2

. (6.68)

Задача 6. Показать, что в однородной изотропной турбулентности разло-

жения спектральных величин в ряд Тейлора имеют вид ([33]):

(

k) = C

ij`m

+ 0(k

E(k) = Ck

+ 0(k

)

Решение. В окрестности точки k = 0 в общем случае имеем:

(

k) = C

+ C

ij`

+ C

ij`m

+ 0(k

). (6.69)

Вследствие уравнения неразрывности (6.46) получаем:

+ C

ij`

+ C

ij`m

+ 0(k

) = 0 ,

что возможно при всех значениях

k → 0 лишь при C

= 0. Тензор Φ

обладает следу-

ющими свойствами:

(

k) = Φ

(−

k) = Φ

∗

(

k),

т.е. является эрмитовским, а форма Φ = x

∗

(

k) ≥ 0 является эрмитовой. При доста-

точно малых k, подставляя сюда ( 6.69), получим выражение Φ = x

∗

ij`

, меняющее

знак при изменении направления

k, поэтому C

= 0. Разложение E(k) следует из ( 6.49)

и четности функции E(k).

Задача 7. Найти связь между константами в "законе 5/3 "и "законе 2/3 "

Колмогорова-Обухова. (Дж.К.Бетчелор ([33]), T.D.Dickly, G.L.Mellor [46]).

Решение. Рассмотрим корреляционную функцию:

R =< (∆~v)

>= R

+ 2R

= (7A

/3)(εr)

2/3

. (6.70)

Здесь учтено соотношение ( 6.5). Из (6.29), (6.44) и (6.49) следует:

R(r) = 4

∞

E(k)

1 −

sin kr

dk. (6.71)

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 185

Для вычисления разобьем (6.71) на три интеграла, соответствующие энергетическому

k < k

, инерционному k

< k < k

и вязкому k > k

интервалам. В первом интеграле

подинтегральное выражение содержит малый множитель 1 − sin kr/kr ' k

, так как

k ∼ `

−1

, r ∼ r

, поэтому k

∼ Re

−3/2

. Третий интеграл дает вклад, не зависящий от

r, т.к. sin kr/kr → 0, а функция E(k) в вязком интервале резко убывает. Распространяя

пределы интегрирования во втором интеграле k

→ ∞, k

→ 0, получим:

(εr)

2/3

≈ 4

∞

2/3

5/3

1 −

sin kr

dk =

(εr)

2/3

Отсюда находим

≈ 2, 068A

Из экспериментальных данных следует (6.6) A

= 1 , 9, тогда A

= 0.92.

Задача 8. Получить в координатной и спектральной формах уравнение

Корсина, описывающее корреляционную функцию температуры B

T T

(r) =<

> для однородной изотропной турбулентности:

∂B

T T

(r, t)

∂t

= 2

∂

∂r

LT,T

(r, t) + a

∂B

T T

(r, t)

∂r

∂Φ

T T

(

k, t)

∂t

= A

(

k) − 2ak

T T

(

k),

где

LT,T

=< v

(k) = ik

LT,T

− B

T,LT

T T

- фурье-образ функции B

T T

. (S.Corrsin [16]).

Решение. Исходим из уравнения теплопроводности в форме:

∂T

+ v

∂T

∂x

= a

∂

∂x

, (6.72)

где положим T =< T > +T

. Вследствие однородности < T >= const среду будем

считать неподвижной в среднем < v >= 0, так что ~v ≡

пульсационные скорости.

Записывая уравнение (6.72) в точках M и

M аналогично (6.34), (6.35), умножая пер-

вое уравнение на

, второе на T

, складывая их, осредняя и переходя к однородной

координате ~r =

˜x −~x, получим уравнение:

∂ < T

∂t

∂

∂r

< v

> − < T

˜v

+ 2a

∂

< T

∂r

. (6.73)

Для изотропной турбулентности

< v

>= B

LT,T

/r.

Подставляя в (6.73), получим искомое уравнение. Выполняя преобразование Фурье урав-

нения (6.73), найдем спектральную форму этого уравнения. Функция A

(k) обладает

свойством, аналогичным (6.59):

(

k)d

k = 0.

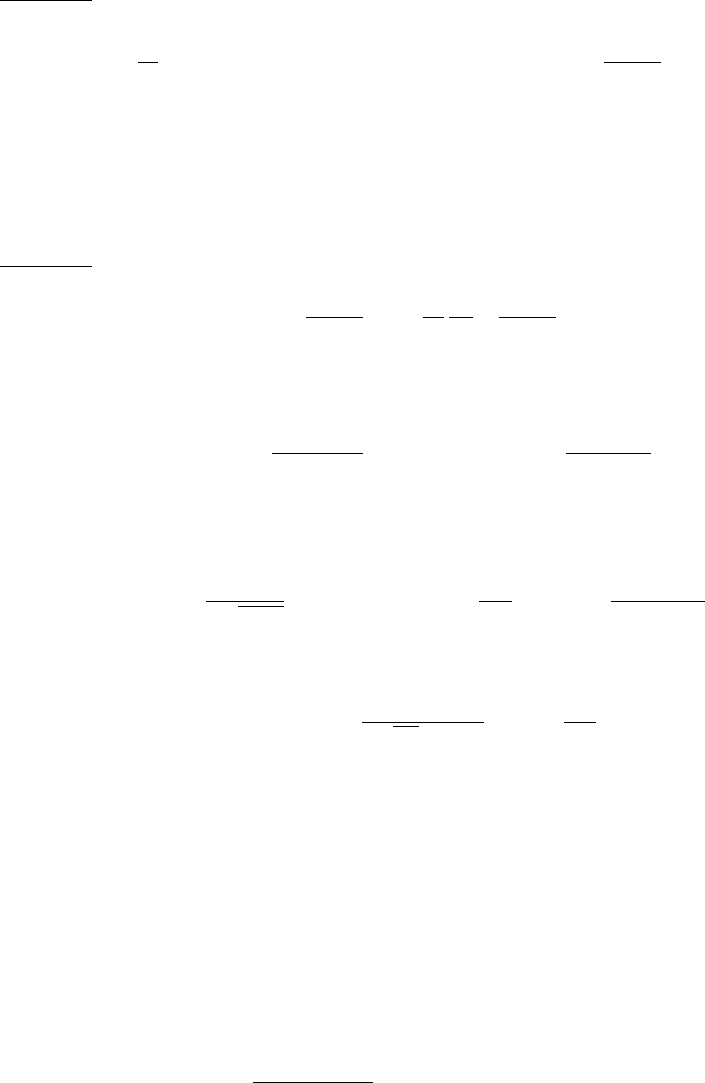
186 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Задача 9. Показать, что если B

T T

(r) стремится к нулю при r → ∞ быст-

рее, чем r

−2

, а B

LT,T

- быстрее r

−1

, то в однородной изотропной турбулентно-

сти несжимаемой жидкости сохраняется величина, называемая инвариантом

Корсина (S.Corrsin [47]):

K =

∞

T T

(r)dr.

Решение. Умножая уравнение Корсина для B

T T

(r) (см.задачу 8) на r

и интегрируя,

получаем:

max

T T

(r)dr = 2r

max

LT,T

+ 2ar

max

∂B

T T

∂r

max

Отсюда с учетом принятых допущений в пределе r

max

→ ∞ получаем искомый резуль-

тат.

Задача 10. Найти асимптотическое поведение корреляционной функции

пульсаций температуры B

T T

(r, t) и среднеквадратичной пульсации темпера-

туры < T

> на стадии вырождения турбулентности (S.Corrsin [47]).

Решение. При B

LT,T

= 0 из уравнения Корсина (см.задачу 8), получаем:

∂B

T T

∂t

= 2 a

∂

∂r

∂B

T T

∂r

(6.74)

уравнение аналогичное уравнению теплопроводности в трехмерном пространстве, кото-

рое имеет решение:

T T

(r, t) =

(8πat)

3/2

T T

, 0)exp

−

(~r −

)

8at

. (6.75)

После интегрирования по условным переменным в сферической системе координат по-

лучаем:

T T

(r, t) =

√

2πat

∞

T T

, 0)sh

4at

exp

−

− (r

)

8at

. (6.76)

В пределе при t → ∞ находим асимптотическое выражение:

T T

(r, t) ≈

√

2π(at)

3/2

exp

−

8at

, (6.77)

где K - инвариант Корсина (см.задачу 9).

Определим спектральную плотность пульсаций температуры:

< (T

)

∞

(k)dk. (6.78)

Из определения B

T T

(r) и Φ

T T

(r) следует

(k) = Φ

T T

(k)k

/2π

Интегрируя уравнение Корсина в спектральной форме (задача 8) и используя свойство

(k), получаем:

∂ < (T

)

∂t

= −2a

∞

(k)dk. (6.79)

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 187

Из (6.77) получим закон вырождения турбулентных пульсаций температуры:

< (T

)

>= B

T T

(0, t) ≈

√

2π(at)

3/2

. (6.80)

Задача 11. Найти корреляционную функцию и спектральную плотность

пульсаций температуры для локально-изотропной турбулентности в инер-

ционном и вязком интервалах при больших числах Рейнольдса и Пекле

(Re = `v/ν, P e = `

v/a)(А.Н.Обухов [48], S.Corrsin [47]).

Решение. При развитой турбулентности происходит дробление вихрей, имеющих

температурную неоднородность < (T

)

>. Этот процесс приводит к тому, что неод-

нородности температуры сосредоточиваются в мелких вихрях, а затем эти неоднород-

ности сглаживаются вследствие молекулярной теплопроводности. Следовательно, как

и в теории Колмогорова, где существует поток кинетической энергии пульсационного

движения вверх по спектру, здесь существует поток энергии пульсаций температуры

вверх по спектру. Найдем соответствующую величину диссипации энергии. Умножая

уравнение теплопроводности

∂T

∂t

+ v

∂T

∂x

= a

∂

∂x

(6.81)

на T

, осредняя и интегрируя по достаточно большому объему, на границах которого

< v

>= 0, получим

< (T

)

> d

r = −

*Ã

∂T

∂x

!Ã

∂T

∂x

r. (6.82)

Отсюда следует, что величиной потока тепловой энергии по спектру является ε

= a <

(∂T

/∂x

)

>. Эта же величина отбирается от крупных вихрей размером ` с неодно-

родностью температуры ∆T и скорости ∆v: ε

= ∆v(∆T)

/`. Если число Прандтля

P r = ν/a ∼ 1, как это обычно бывает в газах, размеры вихрей, в которых происходит

вязкая диссипация кинетической энергии и вихрей, в которых происходит диссипация

тепловой энергии, оказываются одного порядка r

∼ `Re

−3/4

Используем теорию размерностей. В общем случае имеются следующие размерные ве-

личины:

] =

(∆T )

, [E] =

, [a] = [ν] =

Поэтому в общем случае корреляционные функции пульсационной температуры в локально-

изотропной турбулентности имеют вид:

< (∆T

)

>= ε

, P r), (6.83)

(k) = ε

5/4

3/4

ϕ(kr

, P r). (6.84)

В инерционном интервале не должно быть зависимости от a и ν, поэтому единственными

параметрами являются ε

, ε, r.

Из размерности получаем:

< (∆T

)

>= C

−1/3

2/3

, (6.85)

188 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

(k) = C

1/3

5/3

. (6.86)

Постоянные C

и C

связаны соотношением C

= 10C

/9Γ(1/3) (аналогично задаче 7). В

вязком интервале (r < r

) неоднородности температуры малы вследствие молекулярной

вязкости и теплопроводности, поэтому:

∆T

= T

(~x + ~r) − T

(~x) = ~r · ∇T.

Подставляя в выражение для ε

, получим:

< (∆T

)

. (6.87)

6.5 Неоднородное турбулентное движение среды

Турбулентное движение среды в практически интересных случаях, к которым отно-

сятся движение газа с большими скоростями у поверхностей тел, течения в трубах и

каналах и т.д., обычно является неоднородным. Неоднородности вызываются наличием

поверхностей раздела или пространственной зависимостью параметров среды (скоро-

сти, плотности, температуры, давления и т.п.). Для решения таких задач необходимо

иметь уравнения, описывающие турбулентное движение неоднородных сред. Как обсуж-

далось в разделе 6.2.3, мгновенные распределения скоростей удовлетворяют уравнени-

ям Навье-Стокса, а уравнения для средних значений гидродинамических параметров

можно получить, используя процедуру осреднения, описанную в разделе 6.2.3, поэтому

основным способом получения уравнений движения неоднородной турбулентной среды

будет осреднение соответствующих уравнений для мгновенных распределений парамет-

ров. Рассмотрим вначале несжимаемую, а затем перейдем к сжимаемой среде.

6.5.1 Уравнения Рейнольдса

Уравнения движения неоднородной несжимаемой жидкости имеют вид:

∂v

/∂x

= 0 . (6.88)

∂v

∂t

∂v

∂x

= −

∂ρ

∂x

+ ν

∂

∂x

, (6.89)

В турбулентном потоке скорость и давление можно представить в виде суммы средних и

пульсационных величин v

=< v

> +v

, ρ = hρi+ρ

. По определению средних величин <

>= 0, < p

>= 0. Для сокращения записи далее знаки осреднения у средних значений

параметров будут опускаться в тех случаях, когда это не вызывает недоразумений, так,

например, далее hρi ≡ ρ, hv

i ≡ v

. После подстановки разложений величин на средние

и пульсационные значения в уравнения (6.89) и (6.90) и осреднения получим:

∂v

/∂x

= 0 . (6.90)

∂v

∂t

+ v

∂v

∂x

= −

∂ρ

∂x

+ ν

∂

∂x

−

∂

∂x

i, (6.91)

6.5. НЕОДНОРОДНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 189

Уравнения (6.91), (6.90) отличаются от уравнений ламинарного движения только по-

следним членом в (6.91). Объединяя его с членом, учитывающим вязкое трение, запи-

шем их в дивергентном виде:

∂v

∂t

+ v

∂v

∂x

= −

∂ρ

∂x

∂τ

∂x

, τ

= ρν

∂v

∂x

− ρhv

i. (6.92)

Здесь τ

- тензор напряжений, состоящий из тензора вязких и турбулентных напряже-

ний. Последние называются напряжениями Рейнольдса, а уравнения (6.91) - уравнени-

ями Рейнольдса. Применим уравнения Рейнольдса к описанию практически важного

случая стационарного пограничного слоя в предположениях, обычных для теории по-

граничного слоя, а именно, полагая, что:

1. поперечный размер вдоль оси Y мал по сравнению с продольным размером вдоль

координаты X, т.к. ∂/∂x ∼ Re

−1/2

∂/∂y.

2. давление считается постоянным поперек пограничного слоя,

3. между скоростями по осям X и Y выполняется соотношение

u ∼ Re

1/2

v >> v.

В результате получим:

ρu

∂u

∂x

+ ρv

∂u

∂y

= −

∂ρ

∂x

∂(r

τ)

∂y

, (6.93)

∂u

∂x

∂v

∂y

= 0 . (6.94)

Здесь α = 0; 1 соответственно в плоском и осесимметричном случаях, r - текущий ради-

ус, отсчитываемый от оси симметрии обтекаемого тела или канала. Общее напряжение

трения равно:

τ = ρν∂u/∂y − ρ < u

> . (6.95)

Перейдем к рассмотрению сжимаемого газа с переменными коэффициентами переноса.

Этот случай уже реально описывает движение высокотемпературных сред, например,

в пограничном слое при входе космических аппаратов в атмосферу, где вследствие вы-

соких скоростей на внешней части

пограничного слоя движение является сверхзвуковым, т.е. необходимо учитывать

сжимаемость газа; температура поперек пограничного слоя изменяется на тысячи гра-

дусов, поэтому вязкость и теплопроводность газа также изменяются существенно. Ос-

новная идея, которую мы будем здесь проводить, заключается в сведении уравнений

сжимаемого газа с переменными коэффициентами переноса к уравнениям, по форме

совпадающим с уравнениями движения несжимаемой среды. Исходная система уравне-

ний движения высокотемпературных сред в отсутствие электромагнитных полей имеет

вид [49]:

∂ρ/∂t + ∂ρv

/∂x

= 0 , (6.96)

∂v

∂t

+ ρv

∂v

∂x

= −

∂ρ

∂x

∂τ

∂x

, ρ

∂h

∂t

+ ρv

∂h

∂x

∂ρ

∂t

∂

∂x

) −

∂

∂x

+ q

). (6.97)

190 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Здесь h

= h + v

/2, h - удельная энтальпия газа, выражение для потока тепла примем

в простейшей форме q

= −λ∂T/∂x

, ~q

радиационный поток энергии. Тензор вязких

напряжений:

= η

∂v

∂x

∂v

∂x

−

∂v

∂x

+ ξδ

∂v

∂x

. (6.98)

Коэффициент теплопроводности λ, сдвиговая вязкость η и объемная вязкость ξ, удель-

ная энтальпия являются функциями температуры и давления. Подставим в уравне-

ния (6.96-6.98) вместо всех величин сумму из средних и пульсационных значений и

осредним уравнения, считая течение стационарным. В пограничном слое ρ ≈ const, по-

этому в выражении для теплового потока можно считать αT = α h/c

. Вследствие боль-

шого конвективного переноса вдоль продольной координаты hρui = hρihui + hρ

i ≈

hρihui = ρu, в то время как для поперечной координаты hρvi = ρv + hρ

i. В результате

осреднения уравнения непрерывности получим:

∂ρu

∂x

∂hρvi

∂y

= 0 . (6.99)

Осредним уравнение движения. Его левая часть в проекции на ось Х преобразуется

следующим образом:

ρv

∂u

∂x

∂

∂x

hρv

ui =

∂

∂x

(hρuihui + h(ρu)

i) +

∂

∂y

(hρvihui + h(ρv)

i) = ρu

∂u

∂x

+ hρvi

∂u

∂y

∂

∂y

h(ρv)

Здесь использовано уравнение непрерывности (6.99). При преобразовании членов, содер-

жащих коэффициенты переноса, учтем, что их пульсации обычно малы по сравнению

со средними значениями (см.ниже), поэтому соответствующие члены также малы. В

результате получаем уравнение:

∂u

∂x

+ hρvi

∂u

∂y

= −

∂ρ

∂x

∂r

∂y

. (6.100)

Напряжение трения по форме совпадает с (6.95). При осреднении уравнения энергии

учтем, что пульсационные скорости обычно меньше скорости звука, поэтому

i = hhi + hv

i/2 + hv

i/2 ≈ h + u

/2. (6.101)

После аналогичных преобразований получаем:

ρu

∂h

∂x

+ hρvi

∂h

∂y

∂(r

)

∂y

. (6.102)

Здесь тепловой поток по оси Y равен:

= q + uτ + q

, q = ρa∂h/∂y − ρ < u

> . (6.103)

a = hλ/C

i/ρ - коэффициент температуропроводности. От уравнений турбулентного

движения несжимаемой среды уравнения (6.99), (6.100) отличаются пульсационным

членом h ρ

i, но, т.к. в эти уравнения не входят отдельно величины hρi, hvi, значе-

ние корреляции hρ

i не требуется. Осредним выражения для коэффициентов переноса