Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

5.7. МНОГОЖИДКОСТНАЯ ГИДРОДИНАМИКА 151

– длина свободного пробега электронов, L – характерный макроскопический масштаб

неоднородности распределения электронов. С учетом этого получаем закон Ома в виде

j + j × β = σ(E

∗

∇p

´j

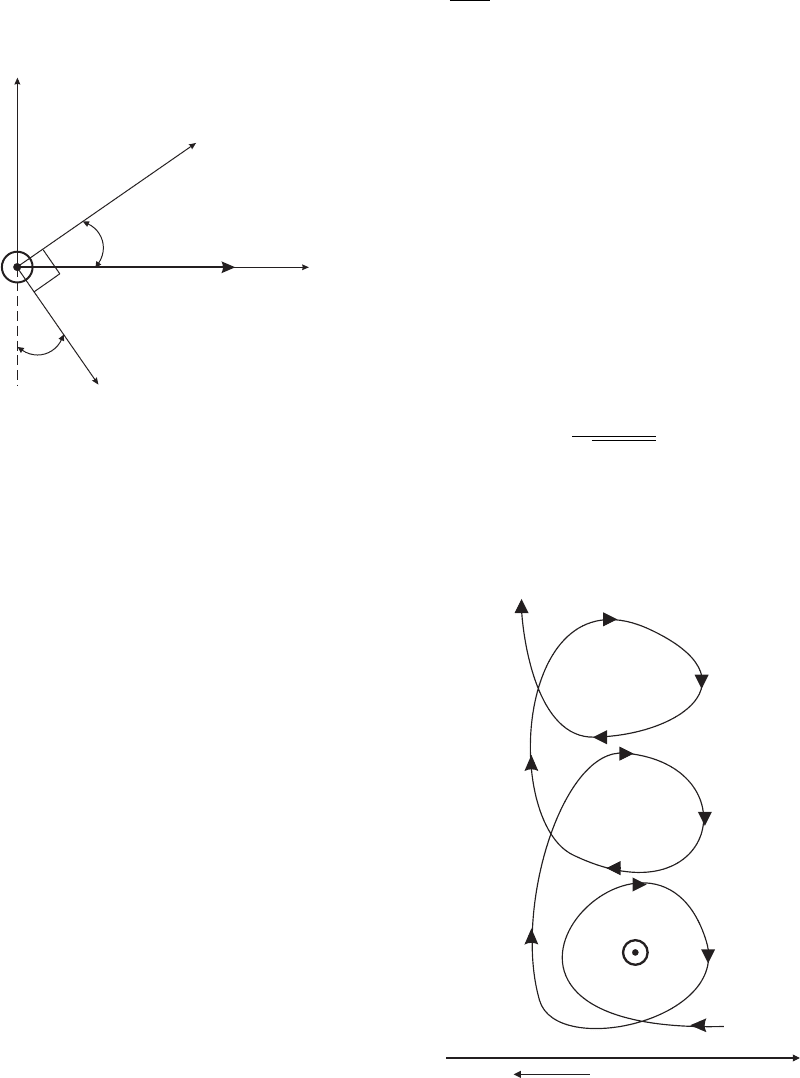
Рис. 5.13: Эффект Холла

Член с ∇p

также часто мал, если k∆T

eEL. Рассмотрим случай, когда магнитное поле

перпендикулярно плоскости тока и электриче-

ского поля j, E ⊥ H (рис.5.13. Проекции закона

Ома в данной системе координат имеют вид

j cos φ + jβ sin φ = σE

∗

j sin φ − jβ cos φ = 0.

Решение системы уравнений определяет угол

между током и электрическим полем φ =

arctan β, и плотность электрического тока

j =

σE

∗

√

1 + β

. (5.96)

Т.е. в замагниченной плазме с немалым пара-

метром Холла кроме составляющей тока вдоль электрического поля возникает и ток,

направленный перпендикулярно H и E

∗

0>DV

0<DV

Рис. 5.14: Дрейфовое движение электронов

при эффекте Холла

Качественное объяснение эффекта Холла

представлено на рис. 5.14 и определяется дрей-

фовым движением электронов в магнитном

поле. Пусть магнитное поле направлено пер-

пендикулярно плоскости листа, а электриче-

ское поле – по горизонтальной оси. Электроны

движутся в магнитном поле по ларморовским

окружностям с изменением скорости в электри-

ческом поле, а значит и с изменением радиу-

са окружности R = mvc/eH, поэтому, прохо-

дя участок АВ электроны разгоняются, а на

участке СD тормозятся, при этом радиус из-

меняется так, что возникает смещение центра

ларморовского кружка, т.е. дрейф электронов

в направлении, перпендикулярном H, E

∗

, что

приводит к току Холла. Выражение для тока

Холла, полученное таким образом, предполага-

ет, что вначале можно провести усреднение по

столкновениям, т.е. ввести эффективную силу

трения, а затем магнитное поле уже действу-

ет на усредненное движение, т.е. сила Лорен-

ца определяется дрейфовой скоростью, следо-

вательно, должно выполняться неравенство ω

τ ¿ 1. В другом предельном случае

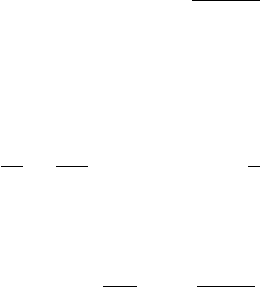
152 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

τ ¿ 1 между столкновениями в скрещенных и магнитных полях электрон совершает

дрейф со скоростью

др

= c

E × H

Интерпретацию тока Холла количественно можно получить из уравнения движения

электронов в стационарном случае, разлагая движение на составляющие по нормали и

касательной магнитных силовых линий:

−n

≈ − e

E +

× H

− mν

Подставляя выражение для скорости электронов через дрейфовую скорость, получим

mν

∗

mcν

× H.

Отсюда и следует вышеприведенная интерпретация эффекта Холла.

5.8 Граничные и внешние условия в гидродинамике

В гидродинамике могут существовать поверхности, на которых физические величины

могут терпеть разрывы. Разрыв называется сильным, если сама величина не является

непрерывной при пересечении поверхности {a} 6= 0, где фигурными скобками обозначе-

на разность величины по обе стороны поверхности {a} = a

(1)

−a

(2)

. Разрыв называется

слабым, если сама величина непрерывна, а разрыв претерпевает ее первая производная.

5.8.1 Общее граничное условие

Получим общее граничное условие для произвольной величины. При выводе интеграль-

ного уравнения переноса (5.2) рассматривался неподвижный объем V , ограниченный

поверхностью S. В случае движущегося объема в этом уравнении в правой части нуж-

но заменить скорость протекания через поверхность v на скорость движения жидкости

относительно движущейся поверхности v −v

. Кроме этого, для движущейся поверхно-

сти необходимо учесть изменение величины поверхности.

Пусть α

- поверхностная плотность величины ξ (заряда, энергии). Полная поверх-

ностная величина равна

dS. Изменение за время dt равно

S(t)

αdS =

S(t+dt)

α(t + dt)dS −

S(t)

α(t)dS =

S(t)

[α(t + dt) − α(t + dt)]dS+

S(t+dt)

α(t)dS −

S(t)

αdS.

За время dt элемент поверхности dS смещается на v

dt. Разложим вектор скорости

поверхности на нормальную и тангенциальную к поверхности скорости V

= v

+ v

sτ

компоненты. Выберем на поверхности систему координат, с осью z перпендикулярно к

поверхности, а оси x и y – совпадающими с направлениями главных кривизн (см. рис.

5.15).

5.8. ГРАНИЧНЫЕ И ВНЕШНИЕ УСЛОВИЯ В ГИДРОДИНАМИКЕ 153

dx’

dy’

v dtsn

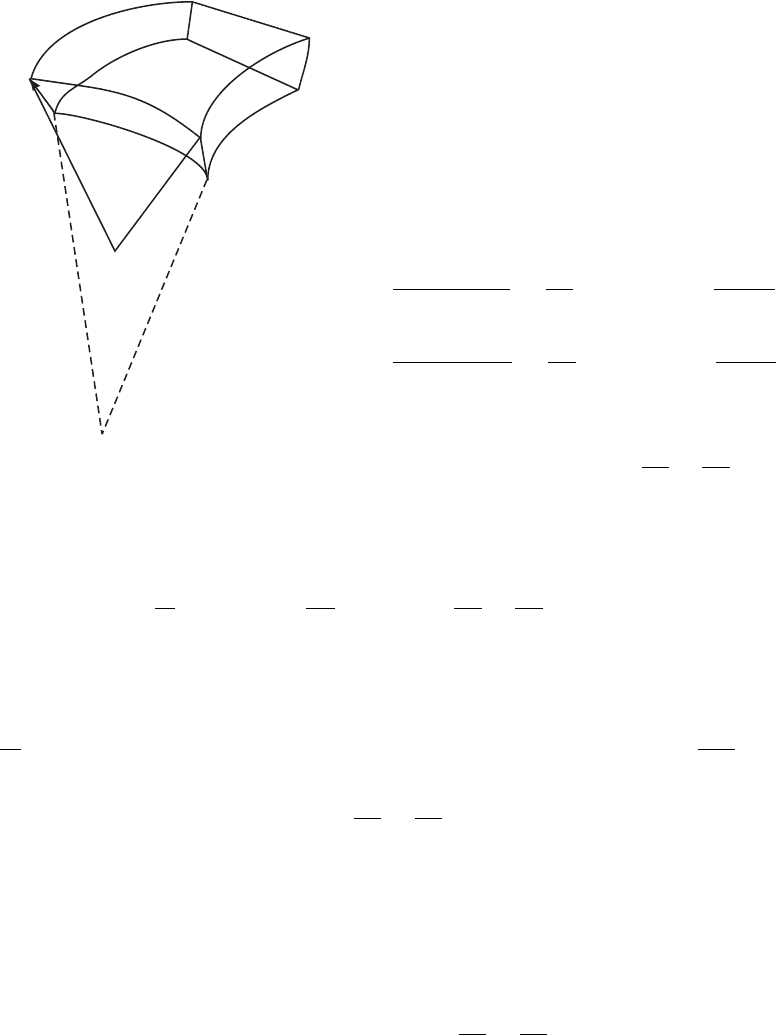
Рис. 5.15: Смещение элементарной площад-

ки поверхности

При тангенциальном смещении элемента

дуги изменения площади не происходит в от-

личие от нормального смещения, при котором

происходит изменение площади поверхности.

Найдем изменение элементарной площадки за

время ∆t. В момент t элемент площади равен

dS = dxdy, в момент t + ∆t элемент площади

равен dS

= dx

. Из подобия треугольников

следует:

+ V

∆t

, dx

1 +

∆t

dx;

= V

∆t

, dy

1 +

∆t

dy.

Изменение площади равно

∆dS = dx

− dxdy =

∆tdS.

Найдем производную от поверхностной величи-

ны для движущейся поверхности:

αdS =

∂α

∂t

dS +

dS.

В результате получаем общее уравнение переноса в интегральной форме для произволь-

ной величины ξ:

ρξdV +

= −

[ρξ(v − v

) + j

] · dA +

dV +

∂α

∂t

dS+

dS. (5.97)

Для получения общего граничного условия выберем элементарный объем, содер-

жащий элементарную площадку dS и высоту ², так что dV = ²dS, причем ²/2 часть

находится по одну сторону поверхности, а вторая ²/2 часть – по другую сторону по-

верхности разрыва. В пределе ² → 0 члены, содержащие объемные величины стремятся

к нулю, а поверхностные члены дают общее граничное условие:

{ρξ(v

− D) + j

ξn

} = α

D. (5.98)

Здесь, в соответствии с традиционными обозначениями нормальная скорость поверхно-

сти V

= D, где D – скорость движения поверхности разрыва (фронта).

Применим это уравнение для различных частных случаев.

Граничные условия для плотности

Полагая ξ = 1, j

= 0 , α

= 0 , получаем граничное условие для плотности

{ρ(v

− D)} = 0, (5.99)

154 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

или

(1)

− D ) = ρ

(2)

− D ). (5.100)

Далее, для потока массы через поверхность разрыва принимается обозначение

j = ρ(v

− D ) = const .

Граничные условия для компонент

Полагая ξ = c

, j

= i

, α

= 0, получаем граничное условие для концентрации компо-

нент сорта m:

{ρc

(m)

− D ) + i

(m)

} = 0 . (5.101)

Динамические граничные условия

ãàç

æèäêîñòü

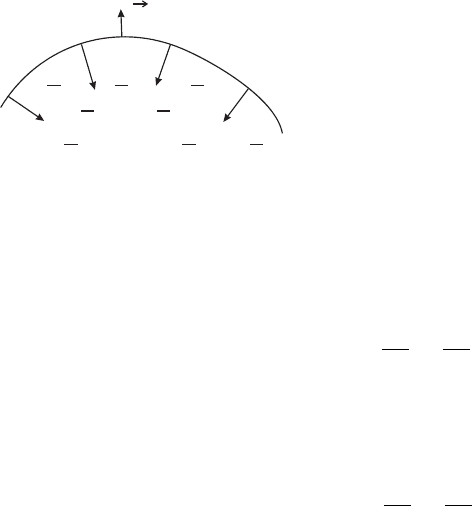
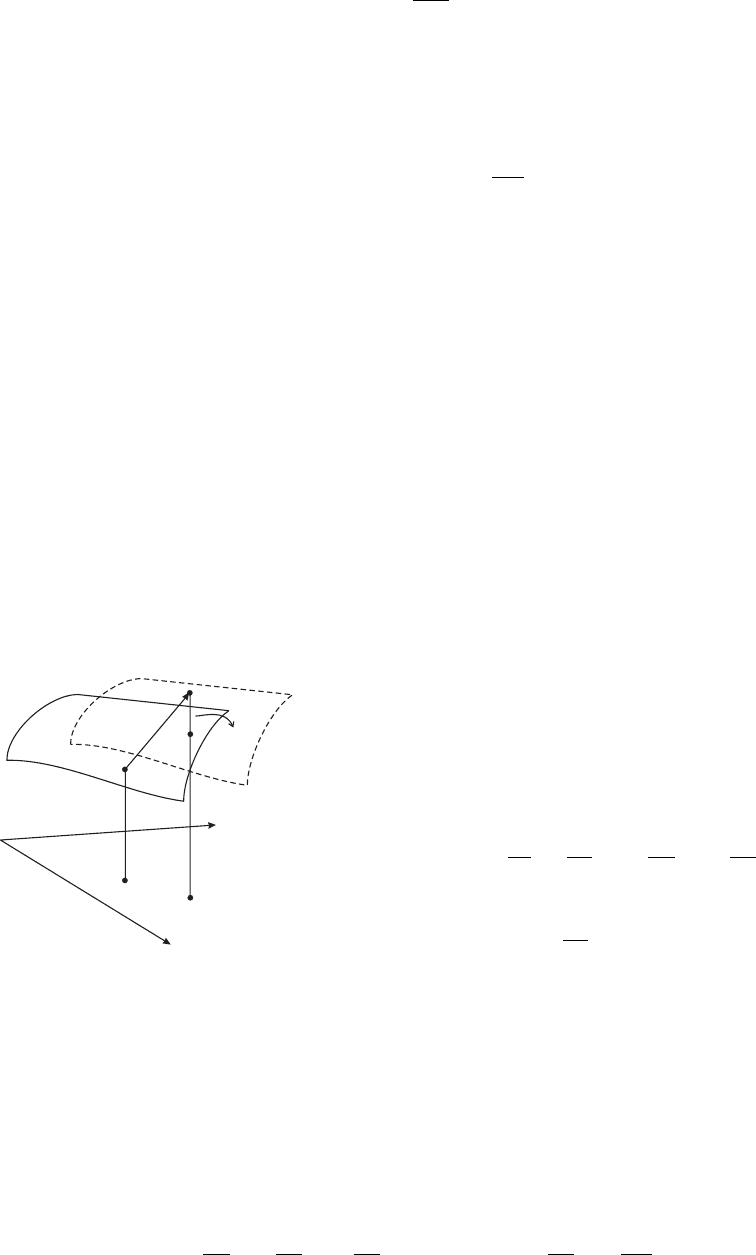
Рис. 5.16: Лапласовское давление на грани-

це двух фаз

При получении граничных условий для нор-

мальных компонент скорости положим ξ = v

= −Π

−T

, α

= 0 . Поверхностного импуль-

са нет, поэтому α

= 0, но в давление необходи-

мо включить лапласовское давление, связанное

с поверхностным натяжением. Из выражения

для свободной энергии

dF = −pdV − S

(э)

dT + αdS,

где S

(э)

– энтропия, dS – элемент поверхно-

сти, следует при dF = 0, T = const, получаем

−p

dV + αdS = 0. Из рис. 5.15, где V

dt = dz,

получаем p

dxdydz = α(1/R

+ 1/R

)dxdydz, откуда

= α

. (5.102)

Это лапласовское давление направлено внутрь жидкой поверхности, так что сила F =

−p

n, где n – единичный вектор нормали к поверхности раздела. Этот член может быть

включен в тензор напряжений, т.е. добавлен к газовому давлению на границе

Π = −

p − α

¶¶

δ + σ.

В результате применения общего граничного условия получаем граничное условие

для нормальной компоненты скорости:

{ρv

− D ) − Π

− T

} = 0 . (5.103)

При получении граничных условий для тангенциальных компонент скорости положим

ξ = v

, j

= −Π

nτ

− T

nτ

, α

= 0 . Граничное условие имеет вид

{ρv

− D ) − Π

nτ

− T

nτ

} = 0 . (5.104)

Вследствие наличия вязкости и при наличии хотя бы с одной стороны диссипативной

среды тензоры вязких и максвелловских напряжений на границе раздела непрерывны,

поэтому с учетом сохранения массы на разрыве, из последнего граничного условия сле-

дует {v

} = 0 .

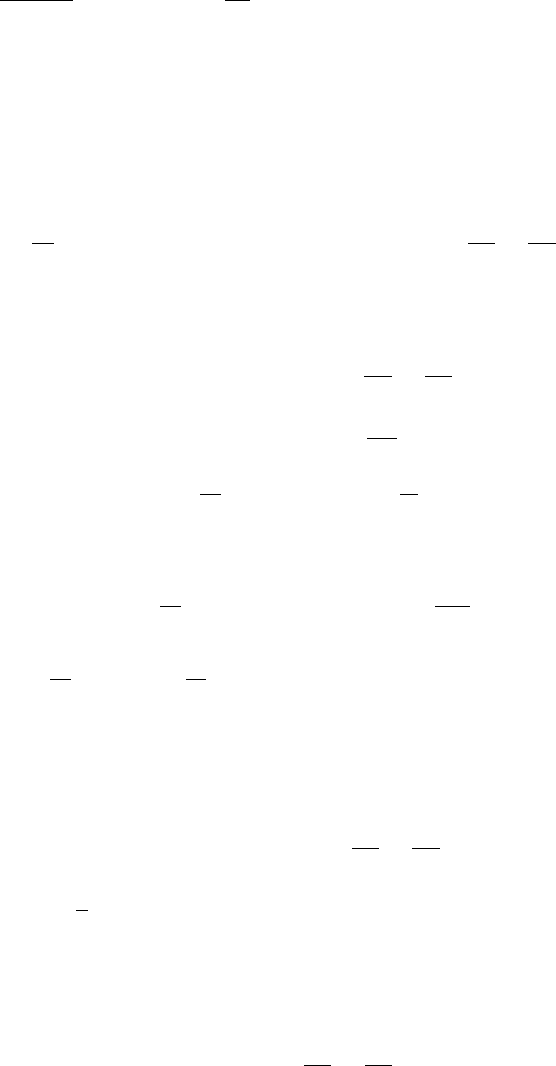
5.8. ГРАНИЧНЫЕ И ВНЕШНИЕ УСЛОВИЯ В ГИДРОДИНАМИКЕ 155

Граничные условия для энергии

Для получения граничных условий необходимо использовать в качестве величины ξ та-

кую величину, которая удовлетворяет общему уравнению переноса. По этой причине

можно в качестве величины ξ выбрать полную энергию или величину, которая имеет

уравнение переноса аналогичное (5.2). Такому уравнению удовлетворяет "полная эн-

тальпия" h

= h + v

/2:

∂rhoh

∂t

+ ∇ · ρvh

∂p

∂t

+ ∇(σ · v − q − q

) + j

· E.

Поверхность фазового раздела газ – жидкость обладает поверхностной энергией

αdS,

(α – коэффициент поверхностного натяжения), которая изменяется при растяжении или

сжатии поверхности. В общем уравнении переноса примем ξ = u

= u + v

/2, α

= α:

j = ρh

v − σ · v + q + q

Подставляя в общее граничное условие, получаем:

{ρ(u +

)(v

− D ) + ρh

− Π : vn + q

} = α

D. (5.105)

Разность энтальпий газовой и жидкой фаз есть теплота испарения, поэтому эти гранич-

ные условия можно преобразовать к следующему виду ({A}

= A

− A

{ρu

− D) − ¦ : vn} = α

D, (5.106)

{jv + pn − σ · n} =

αn

u +

+ pv

+ q

Преобразуем второе уравнение, умножая первое уравнение на nD и складывая со вто-

рым, получим

jh + j

+ pD − σ : nv + q

αD

или

− v · D +

− σ : n(v − D) + q

= −j{h},

т.к. {jD

} = 0. Разность {h} = h

− h

= r

исп

– удельная теплота фазового перехода. В

результате получаем следующие граничные условия:

{j} = 0, (5.107)

{jv + pn − σn}

= αn

, (5.108)

(v − D)

− σ : n(v − D) + q

= jr

исп

. (5.109)

Итак, из интегральных законов сохранения массы, импульса и энергии следует, что

на поверхности разрыва могут существовать скачки нормальной компоненты скорости,

давления и энтальпии ({v

} 6 = 0, { p} 6= 0, { h} 6= 0). Спроектируем (5.108) на n и τ :

{jv

+ p} = α

156 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

(

− µ

∂v

∂y

)

= 0 .

Кроме того, q

= −λ∂T /∂y. Величины, значения которых содержат производные второ-

го порядка (уравнения движения вязкой жидкости можно преобразовать к виду урав-

нения диффузии завихренности Ω = ∇ × v, уравнение энергии можно преобразовать к

уравнению теплопроводности), поэтому эти величины должны быть непрерывными на

границах. Любой скачок величины, испытывающий слабый разрыв диффундирует от

поверхности разрыва за время τ на величину l

∼

√

Dτ. На границах газов и жидкостей с

поверхностями жидких тел могут существовать скачки таких параметров, вызываемые

тем, что существуют области, которые требуют не гидродинамического, а кинетического

описания (т.н. кнудсеновские слои), что приводит к возникновению скачков тангенци-

альной скорости (проскальзывание), температуры, концентрации. Если же используется

более простая модель (например, идеальной вместо вязкой жидкости) и порядок урав-

нения понижается, на границе возникают скачки. Так, для идеальной жидкости {j} = 0,

{jv

} = 0 , { jv

+ p} = α /R.

При этом возможны два случая:

1. ударная волна: j 6= 0, {j} = 0, тогда {v

} = 0 , { jv

+ p} = α /R,

2. тангенциальный разрыв: j = 0, {j} = 0, {v

} 6 = 0, { p} = α/R.

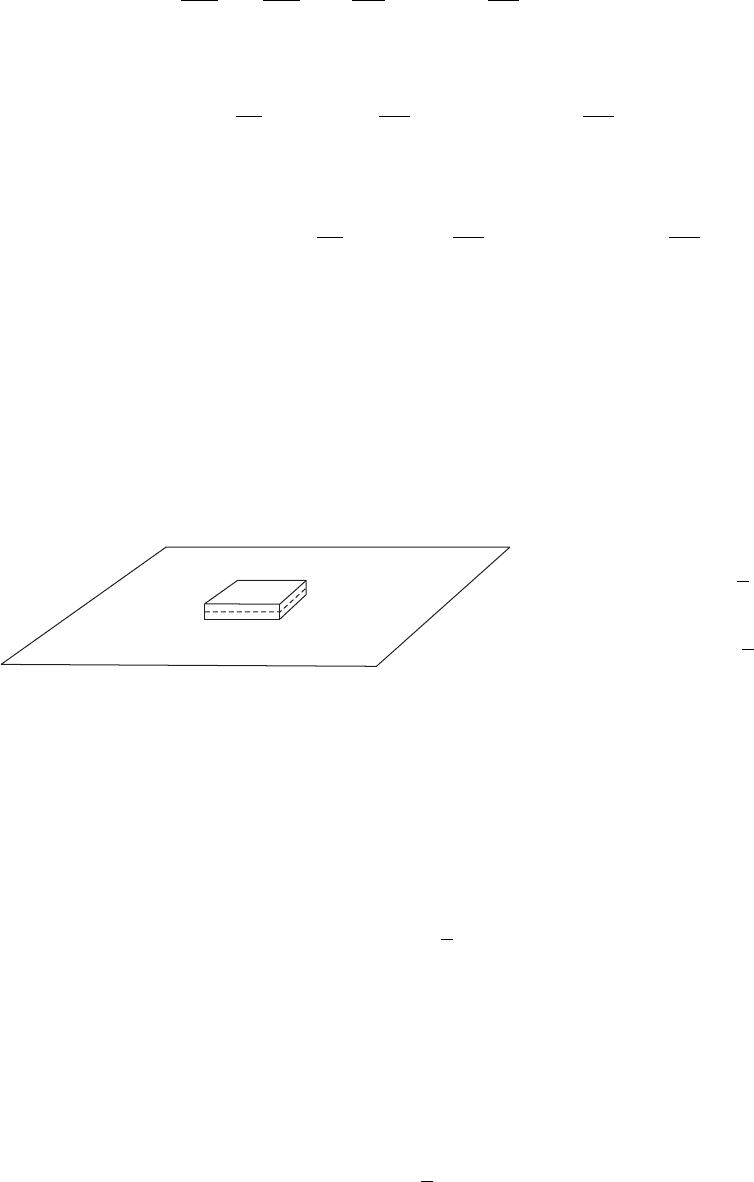
5.8.2 Кинематические граничные условия

Пусть Z = ξ(x, y, t) – уравнение поверхности раздела, которая меняется со временем.

Точка M(x, y, t), лежащая на поверхности, через время dt перейдет в т. M

(x + dx, y +

dy, t + dt), также лежащую на поверхности. Вертикальное смещение поверхности равно

M’

(x,y)

(dx,y+dy)

(x,y,t)x

Рис. 5.17: Смещение поверхности

dξ = ξ(x + dx, y + dy, t + dt) − ξ(x, y, t).

Прибавим и вычтем величину ξ(x + dx, y + dy, t),

тогда, с учетом того, что точки M и M

находятся

на движущейся поверхности, MM = vdt, поэтому

dξ

∂ξ

∂t

+ v

∂ξ

∂x

+ v

∂ξ

∂y

или

∂ξ

∂t

+ v

· ∇

ξ.

Т.к. Z = ξ(x, y, t) – уравнение поверхности, одинако-

вое для верхней и нижней сторон, величина ξ явля-

ется непрерывной {ξ} = 0. Это граничное условие называется кинематическим.

Граничные условия при наличии вдува или отсоса газа

Получим граничные условия при наличии вдува или отсоса газа, использующиеся в

задачах пограничного слоя. В многокомпонентном газе уравнения пограничного слоя

имеют следующий вид:

∂c

∂x

+ v

∂c

∂y

∂i

∂y

ξ, i = ρD

∂c

∂y

+ κ

∂T

∂y

5.8. ГРАНИЧНЫЕ И ВНЕШНИЕ УСЛОВИЯ В ГИДРОДИНАМИКЕ 157

∂h

∂x

+ v

∂h

∂y

∂q

∂y

, q

= λ

∂T

∂y

+ uτ + q

В отсутствие вдува и отсоса i|

= 0, т.е.

∂c

∂y

= −κ

∂T

∂y

, q

= λ

∂T

∂y

При наличии вдува или отсоса газа

вд

= ρ

− ρ

"Ã

∂c

∂y

+ κ

∂T

∂y

, q

= λ

∂T

∂y

(w)

5.8.3 Граничные условия для электромагнитных величин

Как и в предыдущих разделах будем рассматривать среду, для которой µ = 1, ε = 1. Об-

щий метод получения граничных условий состоит в следующем: вначале из уравнений

Максвелла интегрированием по контурам, охватывающим поверхность раздела, полу-

чаются граничные условия для электрического E и магнитного H полей в неподвижной

системе, а затем, в системе, связанной с поверхностью, движущейся со скоростью v

можно перейти к полям E

∗

, H

∗

по формулам преобразования Лоренца, справедливым

с точностью v/c:

+e/2

-e/2

Рис. 5.18: Граничные условия для нормальных компонент

полей

∗

= E +

v × H,

∗

= H −

v × E,

где v = V

– скорость движения

границы разрыва.

Уравнения Максвелла в инте-

гральной форме для ²-объема, содержащего поверхность, имеют вид

H · dA = (H

− H

)S = 0, или{H

} = 0 .

Для движущейся границы получаем, заменяя H на H

∗

} = {H

} −

× E} = 0,

т.к. v

k H

, H

∗

. Аналогично, для электрического поля уравнение Пуассона в инте-

гральной форме имеет вид

E · dA = 4π

σdS, или{E

} = 4 πσ.

После преобразований Лоренца получаем

∗

} = {E

} +

× H} = 4πσ

∗

т.к. v

k E

, E

∗

, где σ

∗

– поверхностная плотность заряда в сопутствующей системе

координат.

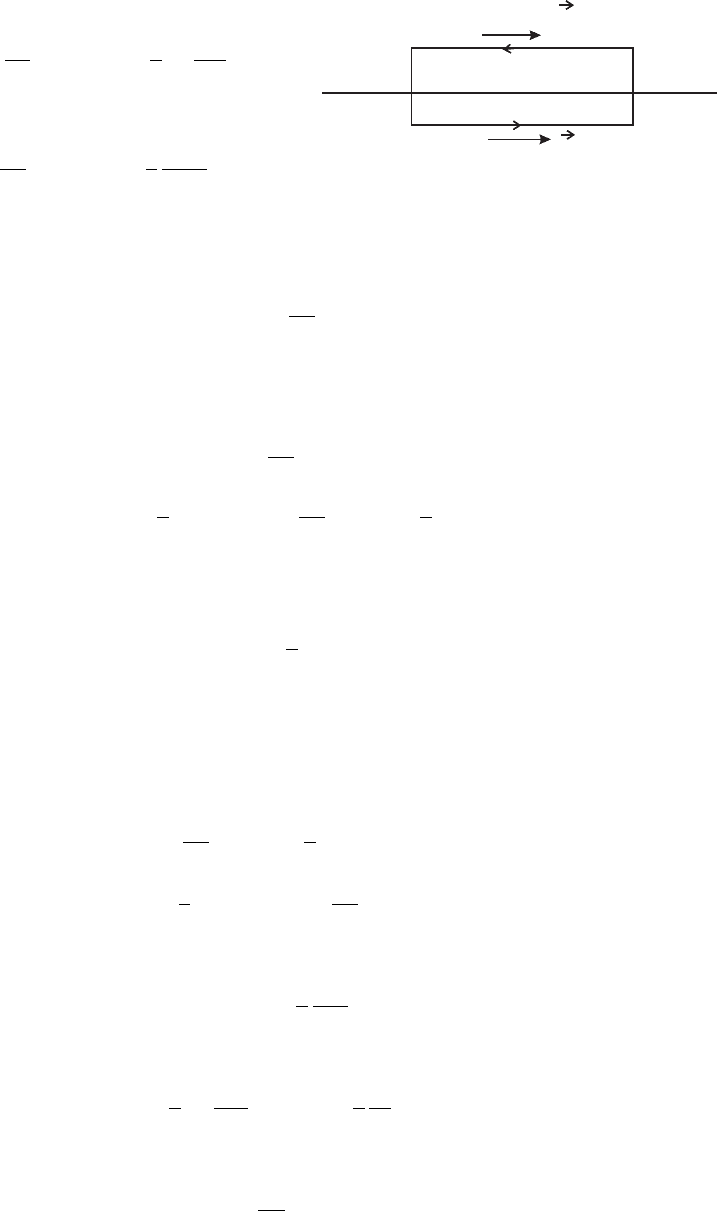
158 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

x+dx

t 1

t 2

Рис. 5.19: Граничные условия для танген-

циальных компонент полей

(∇ × H) · dA =

4π

j · dA +

∂E

∂t

· dA,

или, используя формулу Грина:

H · dr =

4π

j · dA +

∂Φ

∂t

где Φ

E ·dA – поток электрического поля.

После интегрирования по ² контуру, охватыва-

ющему поверхность получаем:

l{H

} =

4π

il ,

где i = I/l – поверхностная плотность тока, т.к. Φ

→ 0 при S → 0.

Вводя единичные векторы направлений по касательной и нормали, получим гранич-

ные условия в виде

} =

4π

i × n,

∗

} = {H

} −

× E} =

4π

∗

× n −

× E

где E

– компонента E k n × τ, i

∗

– поверхностная плотность тока в сопутствующей

системе координат. Аналогично {E

} = 0 ,

∗

} = {E} +

× H}.

В результате получаем следующие граничные условия:

∗

} = 0 ,

∗

} = 4 πσ

∗

} =

4π

∗

× n −

× E

}

∗

} =

× H}

∂

∂τ

Для электрического поля E

граничное условие получается из

∇ × E = −

∂H

∂t

или, интегрируя по контуру уравнение

E · dr = −

∂H

∂t

· dA = −

∂

∂t

H · dA,

получаем соотношение, определяющее контактное сопротивление

} =

∂

∂x

При E = −∇ϕ и {ϕ} = −R

, что приводит к скачку потенциала и образованию

двойного слоя на поверхности.

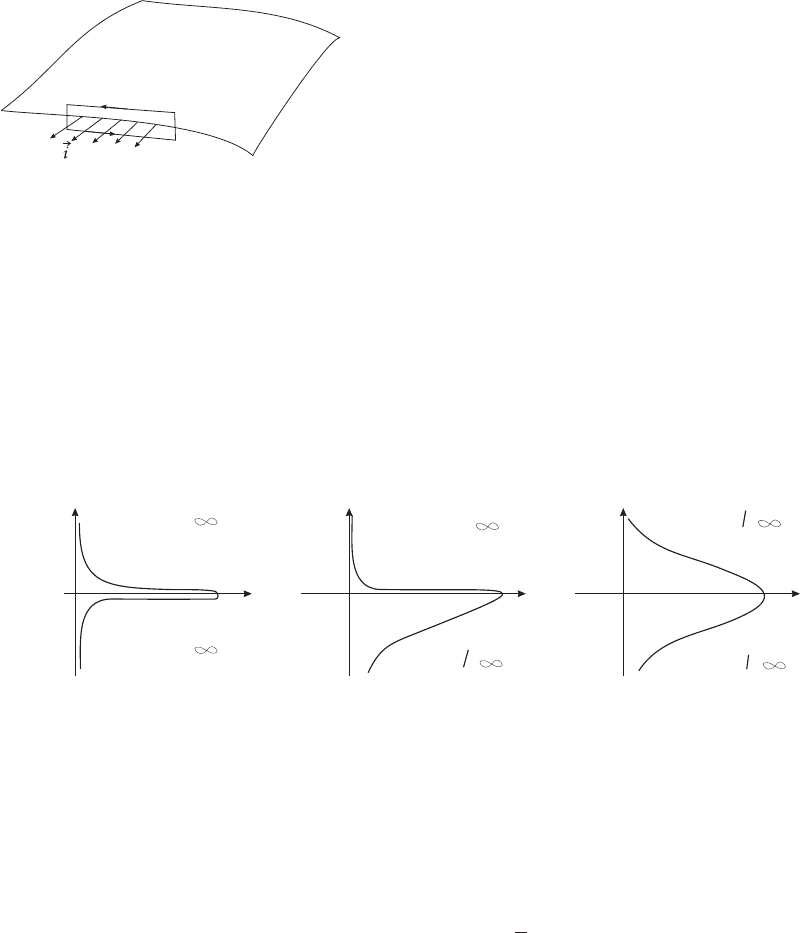
5.9. МНОГОФАЗНЫЕ СРЕДЫ 159

5.8.4 Граничные токовые слои

Граничные токовые слои возникают только в случае сверхпроводящих жидкостей или

твердых тел:

Рис. 5.20: Возникновение граничных токо-

вых слоев

Если рассматривать системы, для которых

полный ток по оси y ограничен:

dZ = I

то при повышении проводимостей с обеих сто-

рон ток выталкивается к поверхности раздела

и i

→ I

σ(Z), i

→ ∞, при Z → 0 возника-

ет поверхностный ток. Если же жидкость толь-

ко с одной стороны является сверхпроводящей,

ток выталкивается с одной стороны и возника-

ет скачок плотности тока, при этом весь ток

протекает по среде с конечной проводимостью

I =

−∞

i(Z)dZ. Скачок тока при этом может также существовать, например,

i(Z) = c

(z) + c

−z/e

, lim

ε→0

i(z)dz = c

∞

i(z)dz = c

+ c

, {H

} = c

но из-за того, что любой скачок {H

} мгновенно (за время τ ∼ e

) диффундирует

на глубину l, поверхностная плотность тока при этом ограничена и {H

} = 0. Отсюда

следует вывод, что если хотя бы с одной стороны среда не является сверхпроводящей,

то тангенциальная компонента магнитного поля непрерывна {H

} = 0 .

s =1

s =2

s =1

s =2

y y

Рис. 5.21: Диффузия магнитного поля в проводящую среду

Граничные условия для тока ∇·j = 0 следуют из условия сохранения электрического

заряда. Это условие выполняется автоматически, т.к. j = (c/4π)∇ × H. Однако иногда

при Re

¿ 1 это уравнение можно не учитывать, т.к. индуцированное магнитное поле

мало|H

инд.

| ¿ |H|, следовательно, ∇ · j = 0 сохраняется, т.е. {j

} = 0. Это условие

можно использовать в виде

{(∇ × H)

} = 0 , или {σ(E +

v × H)

} = 0 .

5.9 Многофазные среды

Многофазная среда отличается от многокомпонентной тем, что каждая фаза занимает

свой объем, например, в сосуде имеется вода и воздух, если их взболтать, то объемы

воды и воздуха (различных фаз) сохранятся (растворимостью воздуха в воде при этом

пренебрегается). Рассмотрим многофазную среду, состоящую из жидкости, газа и твер-

дой фазы. Пусть их суммарные объемы равны соответственно, V

, а полный объем,

160 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

занимаемый средой равен V . Объемная доля фазы

Каждая фаза имеет массу M

= ρ

. Массовая доля фазы

= 1

где полная масса системы

M =

= V

Суммируя по i, получим

. (5.110)

Плотность смеси

ρ =

(5.111)

Для случая двух фаз ϕ

= 1 − ϕ

, X

= 1 − X

ρ = ρ

+ ρ

(1 − ϕ

)

1 − X

откуда, исключая плотность, находим связь между объемной и массовой долями фаз

+ ρ

(1 − ϕ

)

Термодинамические характеристики смеси аддитивны по фазам, а именно, удельные

энтальпия и энтропия равны

h =

(5.112)

s =

(5.113)

Скорость звука в многофазной среде

mix

= ρ

. (5.114)

5.9.1 Задачи по динамике многофазных сред

1. Используя наблюдения за открыванием бутылки шампанского оценить скорость звука

в многофазной (пузырьковой) среде

2. Найти (и построить графически) зависимость скорости звука в многофазной среде

(Drew, Passman p.278)