Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 141

т.е. H/ρ удовлетворяет уравнению Гельмгольца (5.88), следовательно, H/ρ ∼ δl. Отсюда

следует, что магнитное поле "приклеено"к жидким частицам.

Рассмотрим частные случаи применения приближения вмороженного поля.

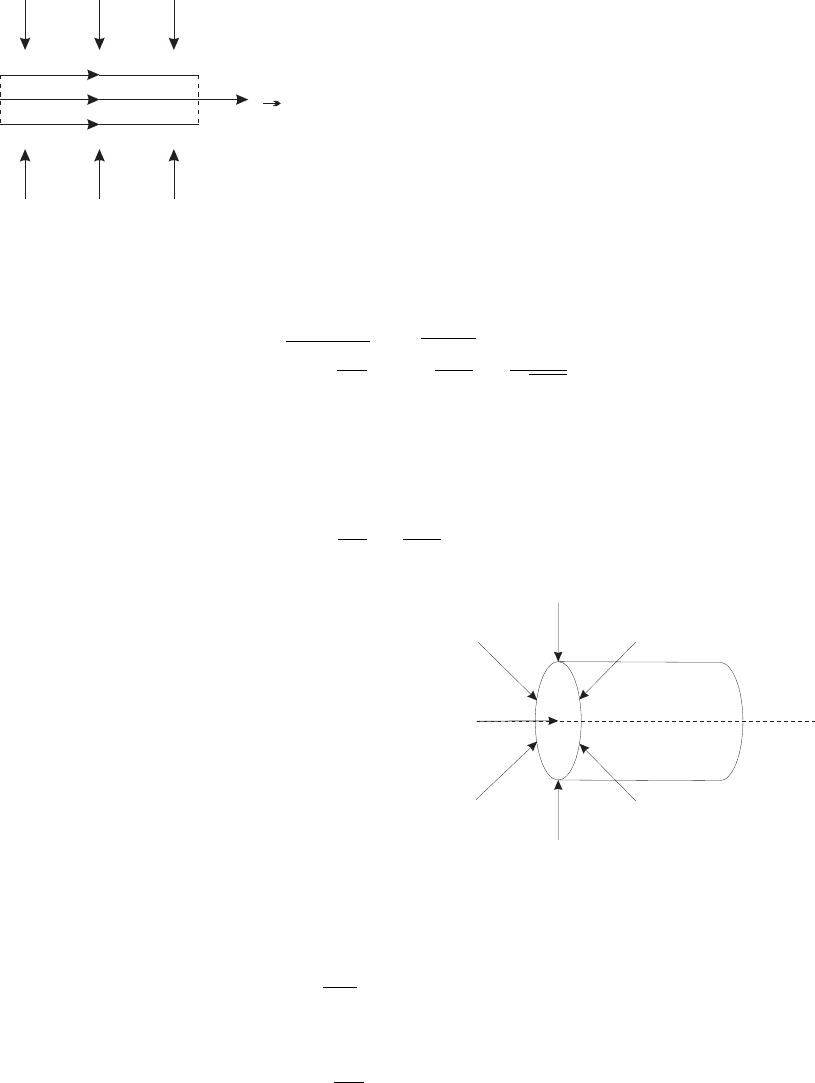
Сжатие вдоль и поперек магнитного поля

ñæàòèå

Рис. 5.5: Сжатие проводящего газа перпен-

дикулярно магнитному полю

Жидкие линии δl следует выбирать вдоль H).

При сжатии вдоль магнитного поля магнит-

ное поле пропорционально линейной массе H ∼

ρδl = const, следовательно, магнитное давле-

ние p

= H

/8π = const т.е. магнитное поле не

изменяется.

При сжатии поперек магнитного поля δl =

const, поэтому магнитное поле пропорциональ-

но плотности H ∼ ρ. Магнитное поле p

/8π ∼ ρ

, что соответствует показателю

"адиабатического"сжатия γ

= ∂ ln p/∂ ln ρ =

2. Поэтому в идеальном проводящем газе рас-

пространяются волны с фазовой скоростью

Альфвена (Alven):

8πρ

√

4πρ

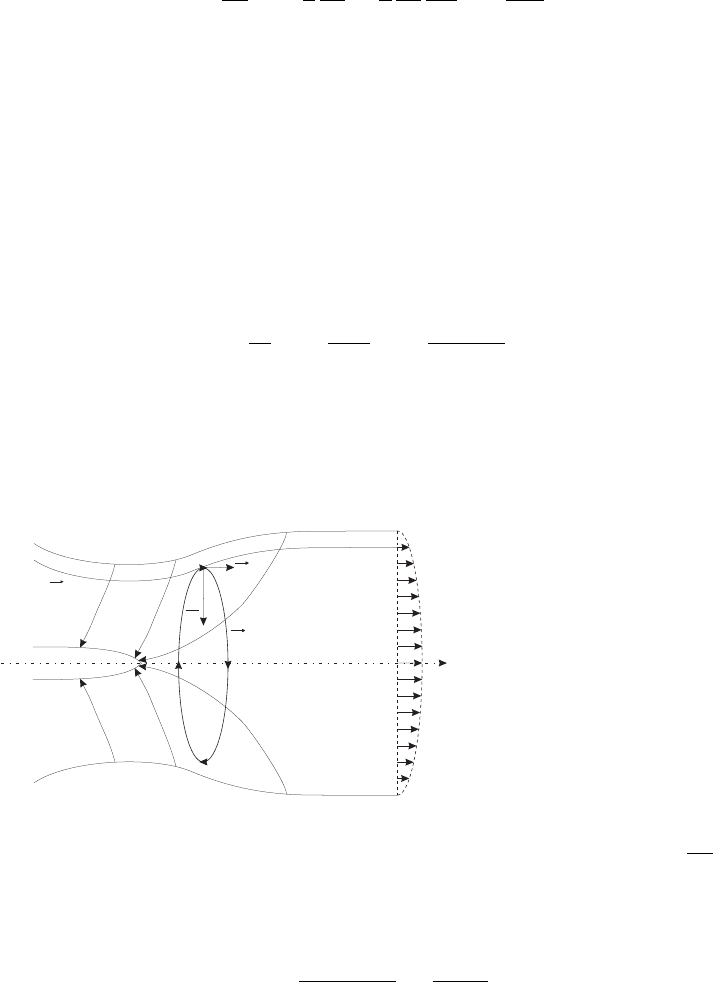
Цилиндрическое и сферическое сжатия

При цилиндрическом или сферическом сжатиях для двух положений имеем

öèëèíäðè÷åñêîå

ñæàòèå

Рис. 5.6: Цилиндрическое сжатие газа в

магнитном поле

откуда следует для

• цилиндрического сжатия ρl

= const, l ∝

−1/2

, H ∼ ρl ∼ ρ

1/2

, магнитное давление

∼ ρ.

• сферического сжатия ρl

= const, l ∝

−1/3

, H ∼ ρl ∼ ρ

2/3

, магнитное давление

∼ ρ

4/3

Движение проводящего газа при Re

¿ 1

При малых магнитных числах Рейнольдса в

уравнении магнитной индукции существенным

является член с магнитной вязкостью. При этом уравнение магнитной индукции

∂H

∂t

= ν

∆H, (5.89)

становится аналогичным уравнению теплопроводности:

∂T

∂t

= χ∆T.

142 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

Если в материале температура на границе T

, а на бесконечности T

∞

, то размер δ, на

который прогреется материал за время t равен δ =

√

χt.

Рассмотрим задачу, в которой на границе со средой с конечной проводимостью при-

ложено переменное магнитное поле H

⊥

= const. Вследствие непрерывности нормальной

составляющей магнитного поля H

⊥

(x) = H

⊥

(0), что следует из ∇ · H = ∂H

⊥

/∂x = 0.

Найдем решение для H

. Пусть H

(x = 0) = H

−iωt

. Тогда из уравнения (5.82)

следует уравнение

∂H

∂t

= ν

∂

∂x

имеющее решение

(x, t) = H

(x) sin ωt,

в стационарной задаче −iωH

= ν

/dx

, откуда H

(x) = H

(0)e

−x/δ

, где глубина

проникновения магнитного поля в среду называется скин-слоем и равна

δ =

4πσω

Силы в магнитной гидродинамике

Магнитная сила может быть выражена через тензор маквелловских напряжений

= −∇

8π

4π

(H · ∇)H = ∇ · T ,

где T – максвелловский тензор напряжений

T =

4π

HH −

В системе координат с осью x k H максвелловский тензор имеет вид

T =







/8π 0 0

0 −H

/8π 0

0 0 −H

/8π







(H, )H

Рис. 5.7: Разложение магнитной силы

т.е. T состоит из всесторон-

него сжатия −H

/8π и растяже-

ния по x с силой H

/8π, приводя-

щей к возможности распростране-

ния магнитных волн.

Иногда удобно разложить маг-

нитную силу на составляющие

вдоль касательной и по нормали

к магнитной силовой линии:

(H · ∇)H = (H · ∇H)τ −

(5.90)

5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 143

5.6.4 Интеграл Бернулли в магнитной гидродинамике

В магнитной гидродинамике интеграл Бернулли применяется, например, при расчете

плазменных двигателей. Из стационарного уравнения движения получаем

∂v

∂s

= −

∂p

∂s

−

∂

∂s

8π

4πρ

· ∇

где s – координата вдоль линии тока. Для интегрирования этого уравнения необходимо

выполнение следующих условий:

• ρ = ρ(p) – баротропность среды,

• ρ = ρ(H) – вмороженность поля (Re

À 1), либо ρ = const,

• Обращение в нуль проекции силы (H · ∇)H на направление линии тока.

Если эти условия выполнены, то (H · ∇)H|

= 0 и имеет место интеграл Бернулли:

ρ(p)

HdH

4πρ(H)

= const .

Приведем примеры, когда (H · ∇H) обращается в нуль или является малым.

Осесимметричное течение в ускорителе

Ëèíèÿ

òîêà

Àíîä

Êàòîä

Рис. 5.8: Осесимметричное течение в ускорителе

Осесимметричное течение в ускори-

теле приведено на рис. (5.8). Прово-

димость среды считается большой,

поэтому примем, что магнитное чис-

ло Рейнольдса велико (Re

À 1),

и справедливо приближение вморо-

женного поля. Задача является осе-

симметричной, поэтому H∂H/∂s =

0, т.е. магнитное поле вдоль силовой

линии постоянно, его величина опре-

деляется из теоремы Ампера:

2πRH =

4π

j · dA,

где j – ток, пронизывающий контур. Магнитная сила имеет составляющую, направлен-

ную только по радиусу:

(H · ∇)H

4πρ

4πρR

sin ϕ.

Если на большом удалении поле скоростей параллельно оси x, то ϕ = 0 и (H ·∇)H = 0,

и для расчета разгона газа может применяться интеграл Бернулли.

Плоское течение в ускорителе

144 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

êàòîä

Рис. 5.9: Плоский электромагнитный ускоритель

Для плоского ускорителя, приведенного

на рис. 5.9 H∂H/∂s = 0 и H

/R = 0, т.к.

R = ∞, поэтому интеграл Бернулли так-

же имеет место.

Высокочастотные силы Миллера

Если на электроны действует осцилли-

рующее с высокой частотой электриче-

ское поле E = E

−iωt

, то в результа-

те осреднения возникает высокочастотная

сила Миллера [4]:

F = −

2mω

∇ < E

> . (5.91)

С помощью этой силы, например, объясняется эффект самофокусировки при распро-

странении пучков заряженных частиц в плазме и газах.

5.7 Многожидкостная гидродинамика

Часто в газе реализуется ситуация, когда можно выделить две или несколько подсистем,

внутри которых равновесие устанавливается быстро, а обмен между подсистемами про-

исходит медленно. Для описания таких систем используется система уравнений баланса

для каждой из подсистем с учетом обмена между подсистемами. Рассмотрим примеры

неравновесных систем.

5.7.1 Релаксационные явления

Релаксационными явлениями называются процессы установления равновесия. Рассмот-

рим среду, находящуюся в состоянии равновесия. Для замкнутых систем это может быть

состояние термодинамического равновесия, а для открытых систем – стационарное со-

стояние, при котором подвод сбалансирован отводом (массы, импульса, энергии и т.п.).

Если система получила малое возмущение, при котором она вышла из состояния тер-

модинамического равновесия или стационарного состояния, то, в отсутствие поддержки

возмущения, система через некоторое время, называемое временем релаксации, снова

вернется в то же состояние равновесия. При слабом отклонении от состояния равно-

весия параметр, описывающий состояние равновесия (рассмотрим пример, когда этим

параметром является энергия системы), удовлетворяет следующему уравнению:

= f(E),

где правая часть может быть представлена в виде разложения вблизи положения рав-

новесия:

f(E) = f(E

) +

∂f

∂E

(E − E

) +

∂

∂E

(E − E

)

+ . . .

5.7. МНОГОЖИДКОСТНАЯ ГИДРОДИНАМИКА 145

При слабом отклонении от равновесия уравнение, описывающее переход в состояние

равновесия, имеет вид, называемый релаксационным уравнением:

= −

E − E

где время релаксации

−1

∂f

∂E

Приведем примеры релаксации в газе.

Поступательная релаксация

При упругом столкновении двух частиц происходит передача энергии от одной стал-

кивающейся частицы к другой ∆² = (2m

)², где m

, m

– массы сталкивающих-

ся частиц. После Z столкновений частица теряет энергию Z∆², поэтому если после Z

столкновений частица потеряет энергию, сравнимую с первоначальной энергий, т.е. при

Z∆² ∼ ² число столкновений, необходимых для установления равновесия, равно

Z =

∆²

Если m

∼ m

, то Z ∼ 1, т.е достаточно нескольких столкновений, чтобы произошло

установление поступательного равновесия.

Рассмотрим более общий случай, относящийся к вращательному, колебательному

и электронному возбуждению молекул. При каждом столкновении частиц существует

вероятность возбуждения внутренних степеней свободы молекул (вращательных, ко-

лебательных и электронных). Пусть при одном столкновении частица теряет энергию

∆ε = δ · ε. Величина δ называется долей "неупругости" процесса. После Z

столкнове-

ний частица теряет энергию, сравнимую с начальной энергией Z

∆ε = ε (грубо можно

считать, что первые Z

− 1 столкновений происходят без изменения энергии, а в каж-

дом Z

-ом столкновении энергия изменяется сразу на величину ∼ ²). Число "активных"

столкновений в единицу времени ν/Z = δν. Время между столкновениями τ = 1/ν, а

время между "активными" столкновениями τ

= 1 /δν = τ/δ. Это время и принимается

за время релаксации для i-процессов. Если ввести вероятность для i процесса в одном

столкновении p

, тогда средняя частота "активных"столкновений ν

= νp

. Вероятность

вычисляется усреднением по максвелловскому распределению частиц.

Вращательная релаксация

Рис. 5.10: Поступательно-

вращательная релаксация

Для упругих столкновений частиц δ

упp

= 2m

. Для вра-

щательных столкновений частиц можно рассмотреть зада-

чу, в которой частица сорта A сталкивается с "гантелью" ,

состоящей из двух масс m

(см. рис.5.10). Доля энергии,

передаваемой из поступательных во вращательные степени

свободы, равна

∆² =

9(2m

+ m

)

²,

следовательно, ²/∆² ∼ 10 , т.е. поступательные и вращатель-

ные степени свободы молекул быстро (после десятка столкновений) приходят в равно-

весие.

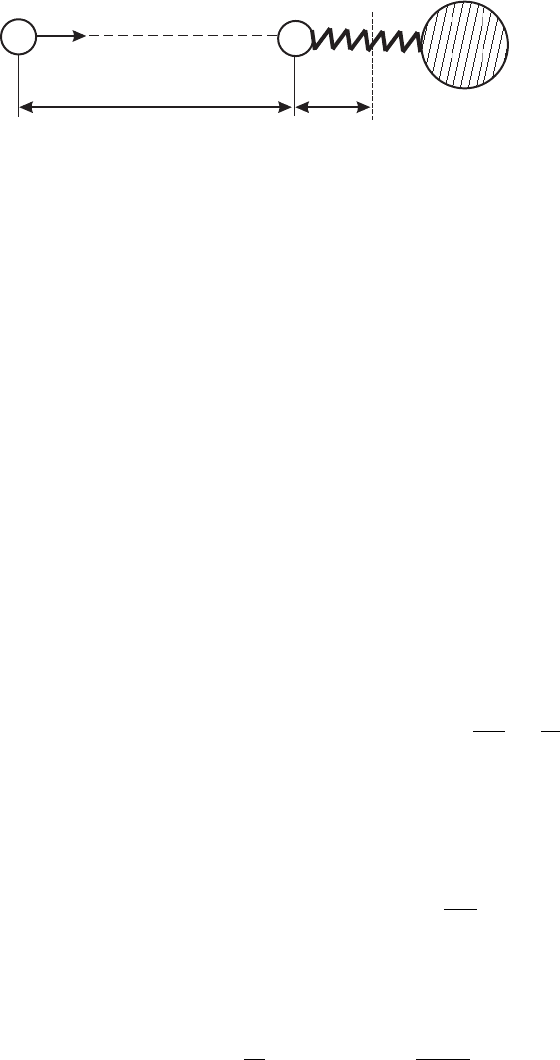
146 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

Колебательно-поступательная релаксация

y=0

Рис. 5.11: Соударение частиц с колебательным возбужде-

нием

Одним из примеров неравновес-

ной среды является молекуляр-

ный газ, в котором возбуждаются

колебательные степени свободы

молекул. Рассмотрим возбужде-

ние колебаний двухатомных моле-

кул. Двухатомные молекулы типа

имеют квант колебательного

возбуждения ¯hω ∼ 0.3 эВ, что со-

ответствует температуре 3480 K.

В нагретом газе могут возбуждаться колебательные степени свободы молекул и в первую

очередь происходит переход v = 0 → 1. Этот переход происходит при столкновениях

молекул, имеющих относительные энергии, превышающие энергетический барьер реак-

ции 0.3 eV . В целях модельного расчета рассмотрим столкновение атома с молекулой,

приведенное на рис. 5.11.

Пусть а – область действия потенциала сталкивающихся частиц. В данной задаче

имеется два характерных времени – время пролета налетающей частицы τ

прол

' a/v и

время колебаний молекулы τ

кол

∼ 1/ω. Если τ

прол

À τ

кол

, налетающая частица будет

медленно сжимать "пружину"при сближении и растягивать при удалении частиц, т.е.

взаимодействие будет адиабатическим с малой вероятностью возбуждения колебаний.

Покажем, что в этом случае вероятность возбуждения колебаний

∼ e

−τ

прол

/τ

кол

∼ e

−aω/v

Рассмотрим наиболее простой случай m

À m

= m, а потенциал взаимодействия

примем в виде U = U

−x/a

, где положим U

= µv

∞

/2.

Уравнение движения атома m в осцилляторе имеет вид (рис. 5.11):

m( ˙y + ω

y) = −

∂U

∂y

Умножим это уравнение на e

iωt

и проинтегрируем по t от −∞ до t с начальными

условиями, соответствующими адиабатическому включению взаимодействия ˙y(−∞) =

y(−∞) = 0. В результате получим уравнение

( ˙y − iωy)e

iωt

= −

−∞

iωt

dt.

Вычисляя квадрат модуля этого выражения и умножая на m/2, получим уравнение,

определяющее изменение энергии осциллятора, вызываемое возмущением

( ˙y

+ ω

) =

2ma

−∞

iωt

Это выражение легко преобразуется в квантовый случай, когда фурье-компонента воз-

мущения на собственной частоте осциллятора может быть заменена в соответствии с

правилами Бора-Зоммерфельда на матричный элемент возмущения между начальным

и конечным состояниями.

5.7. МНОГОЖИДКОСТНАЯ ГИДРОДИНАМИКА 147

Энергия, которую приобретает осциллятор при t → ∞, равна

²(∞) =

2ma

∞

−∞

iωt

= ¯hωp

где вероятность перехода 0 → 1 или в классическом случае возбуждения колебаний

2ma

¯hω

Найдем фурье-компоненту потенциала взаимодействия. Движение налетающей частицы

и частицы осциллятора m в поле U = U

−x/a

= βµv

∞

/2e

−x/a

, где β = U

/(µv

∞

/2))

– параметр, описывающий отношение параметра потенциала и кинетической энергии

налетающей частицы на бесконечности. Интеграл энергии имеет вид

µ ˙x

+ β

µv

∞

−x/a

µv

∞

откуда находим

˙x = v

∞

1 − βe

−x/a

Введем безразмерные переменные ξ = x/a, τ = v

∞

t/a, тогда получим уравнение

dξ

dτ

1 − βe

−ξ

Интеграл этого уравнения

τ =

dξ

1 − βe

−ξ

Полагая 1 − βe

−ξ

= u

, получим уравнение, определяющее движение частицы (зависи-

мость координаты частицы от времени)

τ =

2udu

u(1 − u

)

1 − u

−

1 + u

du = ln

1 + u

1 − u

Отсюда находим

u =

− 1

+ 1

Подставляя зависимость x(t) в выражение для потенциала, получаем

= e

−ξ

1 − u

= 1 − (

− 1

+ 1

)

β ch

(τ/2)

Вычислим фурье-компоненту потенциала

∞

−∞

iωt

(τ/2)

dt =

βv

∞

где интеграл

I =

∞

−∞

iητ

(τ/2)

dτ,

(η = aω/v

∞

) имеет полюс второго порядка в точке τ = iπ, (см. 5.12), т.к. ch τ/2 =

ch iπ/2 = cos π/2 = 0.

148 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

Im t

Re t

2ip

Рис. 5.12: Плоскость интегрирования

Интеграл по верхней части равен

∞

−∞

iη(τ+2πi)

((τ + 2πi)/2)

dτ = e

−2πη

Вычет в точке τ = iπ равен

(1 − e

−2πη

)I = 2πi resf(iπ) =

= 2 πi lim

τ→iπ

−ηπ

(τ − iπ)

ch(iπ/2) +

(τ−iπ)

sh(iπ/2)

= 4πie

−πη

В результате получаем значение интеграла

I = 4πi

−ηπ

1 − e

−2πη

2πi

sh πη

≈ 2πie

−πη

В результате находим фурье-компоненту потенциала

βv

∞

|I|

= 4 π

µv

∞

2βv

∞

−2πη

Соответственно, вероятность перехода равна

∞

2ma

¯hωβ

−2πη

Если учесть, что λ = ¯h/p = ¯h/µv

∞

¿ a, где µv

∞

/2 = µω

, получаем окончательно

(v) = π

µv

2¯hω

−2πaω/v

. (5.92)

Усредним эту вероятность по максвелловскому распределению частиц:

< p

= 4π

∞

−∞

2¯hω

−2πaω/v

√

−mv

/2kT

Подынтегральное выражение содержит функцию e

−φ(v)

, где

φ(v) =

2πaω

Интеграл от этой функции вычисляется методом перевала:

∞

−∞

−α(x−x

)

g(x)dx ≈ g(x

)

π/α.

Экстремум функции находится в точке v

= (πaωv

)

1/3

, значение в этой точке φ(v

) =

3(πaω/v

)

2/3

Усредненная по максвелловскому распределению вероятность перехода

< p

>= 8

√

2π

µv

2¯hω

−3(πaω/v

)

2/3

В результате получаем формулу Ландау-Теллера

(T ) = A(T )e

−BT

−1/3

. (5.93)

5.7. МНОГОЖИДКОСТНАЯ ГИДРОДИНАМИКА 149

Баланс энергии в колебательно-неравновесной системе

Вероятность перехода p

¿ 1, т.е. требуется большое (∼ 10

) число столкновений для

установления равновесия между поступательно-вращательными и колебательными сте-

пенями свободы. В таких условиях баланс энергии разделяется на баланс поступательно-

вращательной (T R с энергией E

T R

) и колебательной (V с энергией E

на единицу объ-

ема) подсистем.

Применяя общее уравнение баланса к подсистемам, получаем уравнения переноса:

∂E

∂t

+ ∇ · (vE

) = −∇ · q

+ Q

−

− E

(T )

V T

∂E

T R

∂t

+ ∇ · (vE

T R

) = −∇ · q

T R

+ P : ∇v +

− E

(T )

V T

Потоки в простейшем случае выражаются через градиенты соответствующих темпера-

тур:

= −λ

V T

∇T − λ

V V

∇T

T R

= −λ

T T

∇T − λ

T V

∇T

Внутренняя энергия колебаний может быть выражена через соответствующую теплоем-

кость dE

= C

. Неравновесная колебательная релаксация используется в технике

в газодинамических и электроразрядных лазерах.

5.7.2 Слабоионизованная плазма в электрическом поле

Другим примером неpавновесной системы является слабоионизованная плазма, поме-

щенная в электрическое и магнитное поля. Рассмотрим сначала случай только элек-

трического поля, встречающийся в электрических разрядах. При достаточно сильных

электрических полях нарушается условие малости нагрева электронов полем по срав-

нению с их кинетической энергией (eEl

/kT ¿ 1) и, соответственно, закон Ома. Это

нарушение возникает вследствие того, что электрическое поле сообщает энергию лег-

ким подвижным электронам, которые в столкновениях отдают ее тяжелым частицам и,

если частота передачи энергии мала по сравнению с частотой установления равновесия

в электронной и ионной подсистемах, то возникает различие (отрыв) в температурах

легких и тяжелых частиц Т

> Т

. В этом случае необходимо использовать отдельно

уравнения баланса энергии для электронов и тяжелых частиц.

Баланс энергии электронов имеет вид

+ n

= j · E − n

− T ) − ∇ · q

. (5.94)

Баланс энергии для тяжелых частиц (газа):

nkT

= n

− T ) − ∇ · q, (5.95)

где векторы потоков энергии для газа в целом и для электронов имеют вид

q = −λ∇T, q

= −λ

∇T

150 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД

При слабой ионизации можно пренебречь теплопроводностью электронов из-за их малой

концентрации. Из (5.94) можно получить оценку отрыва электронной температуры:

mν

= n

− T ),

откуда следует относительная величина отрыва температур

− T

3δ

mν

9δ

eEl

5.7.3 Слабоионизованная плазма в магнитном поле

В магнитном поле может нарушаться условие β = ωτ ¿ 1, что приводит к анизотропии

коэффициентов переноса. Т.к. ω = eH /mc , то вначале это условие нарушается для

электронов. Рассмотрим уравнения движения электронов и тяжелых частиц.

= −∇p

+ ∇ · P

− en

(E +

× H) + R

= −∇p

+ ∇ · P

− Z

E +

× H

− R

Сила трения R

= −mn

− v

) = −mn

, где u

= v

− v

– дрейфовая

(относительная) скорость движения электронов.

Вместо ((v

, v

) введем переменные ((u

, v)), где определены среднемассовая ско-

рость движения среды и дрейфовая скорость электронов

v =

+ m

+ n

≈ v

Складывая уравнения движения атомов и электронов, получим уравнения движения

смеси в целом

= −∇p + ∇ · P +

j × H,

а из уравнения движения электронов, умножив его на e/mν

, найдем ток (закон Ома):

j =

mν

∗

∇p

) +

× H +

T е

3ν

∆j.

Здесь для вязкости электронов использовано выражение

= m

T е

3nQ

T e

T е

3ν

Общая форма закона Ома в двухжидкостной модели имеет вид

j + j × β = σ

∗

∇p

−

− λ

∆j.

Член с инерцией электронов не важен, т.к ν

τ À 1, где ν

– транспортная частота

столкновений электронов, τ – характерное время изменения гидродинамических пара-

метров (этот член пропорционален электронному числу Кнудсена). Член с вязким за-

туханием импульса электронов также мал, т.к он пропорционален (l

/L)

¿ 1, где l