Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

6.3. ЛОКАЛЬНАЯ СТРУКТУРА ТУРБУЛЕНТНОСТИ 171

6.3.4 Особенности двумерной турбулентности

Приведенные выше в настоящем параграфе результаты относятся к обычно реализую-

щемуся в турбулентных потоках случаю трехмерной турбулентности. Однако, если на

поток действуют силы, подавляющие пульсации в каком-либо одном направлении, то мо-

жет возникнуть двумерная (в частности, плоская) турбулентность. Теоретическое зна-

чение и некоторые практические приложения могут иметь также задачи об одномерной

турбулентности. Двумерный или близкий к двумерному характер крупномасштабного

турбулентного движения устанавливается во многих практически важных случаях. В

частности, если в поле силы тяжести имеется распределение плотности жидкости или

газа, соответствующее устойчивой стратификации, то архимедовы силы препятствуют

развитию вертикальных (вдоль силы тяжести) турбулентных пульсаций. Это приводит к

близкому к плоскому характеру крупномасштабной турбулентности в устойчиво страти-

фицированной атмосфере, к возникновению "плоских"следов за телами, движущимися

под водой в океане (с вертикальным размером следа много меньшим его ширины в го-

ризонтальном направлении). Близкую к плоскости форму имеют турбулентные вихри

в непосредственной близости от стенки.

В турбулентных потоках электропроводных сред в магнитном поле существуют си-

лы, способствующие возникновению двумерной структуры пульсаций (в плоскости, пер-

пендикулярной направлению силовых линий магнитного поля). Однако при больших

числах Re мелкомасштабные пульсации обычно остаются трехмерными, хотя при очень

большой интенсивности подавлении пульсации вдоль одной из осей можно добиться дву-

мерной структуры и мелких вихрей (при умеренных числах Re это экспериментально

достигнуто в указанном выше случае воздействия магнитного поля). Мы ограничим-

ся ниже рассмотрением только некоторых особенностей двумерной турбулентности. В

случае движения жидкости в плоскости x

− x

вихрь скорости имеет единственную

отличную от нуля составляющую ω = (rot ~v)

3, направленную вдоль оси x

, т.е. перпен-

дикулярно к плоскости движения. Уравнение для ω имеет следующий вид:

∂ω

∂t

+ v

∂ω

∂x

+ v

∂ω

∂x

= ν

∂

∂x

∂

∂x

. (6.14)

Из (6.14) видно, что изменение ω для каждой "жидкой частицы"

определяется только

стоящим в правой части (6.14) членом с вязкостью ν, описывающим перераспределе-

ние (выравнивание) ω в рассматриваемой области течения. Следовательно, абсолютные

величины |ω| везде в рассматриваемой области течения ограничены либо начальными

значениями |ω|

max

, либо максимальными значениями |ω| на границах. Какого-либо меха-

низма увеличения |ω|

max

под влиянием самого движения жидкости, как видно из (6.14),

не существует. Это является особенностью именно плоского движения; в пространствен-

ном случае вихрь скорости может возрастать под влиянием растяжения вихревых нитей

вдоль их оси (что описывается соответствующими нелинейными членами уравнениях).

Указанная особенность плоского движения позволяет сразу же предположить, что при

плоской турбулентности не будет действовать нелинейный механизм передачи энергии

от крупных вихрей к более мелким, так как такая передача энергии (если бы она су-

ществовала) должна была бы приводить к увеличению производных от скорости по

координатам, т.е. к увеличению ω. Для более подробного выяснения этого вопроса рас-

смотрим в качестве примера изменение во времени энергии турбулентности и величины

Левая часть (6.14) - это производная ω по времени в системе координат, движущейся с "жидкой частицей".

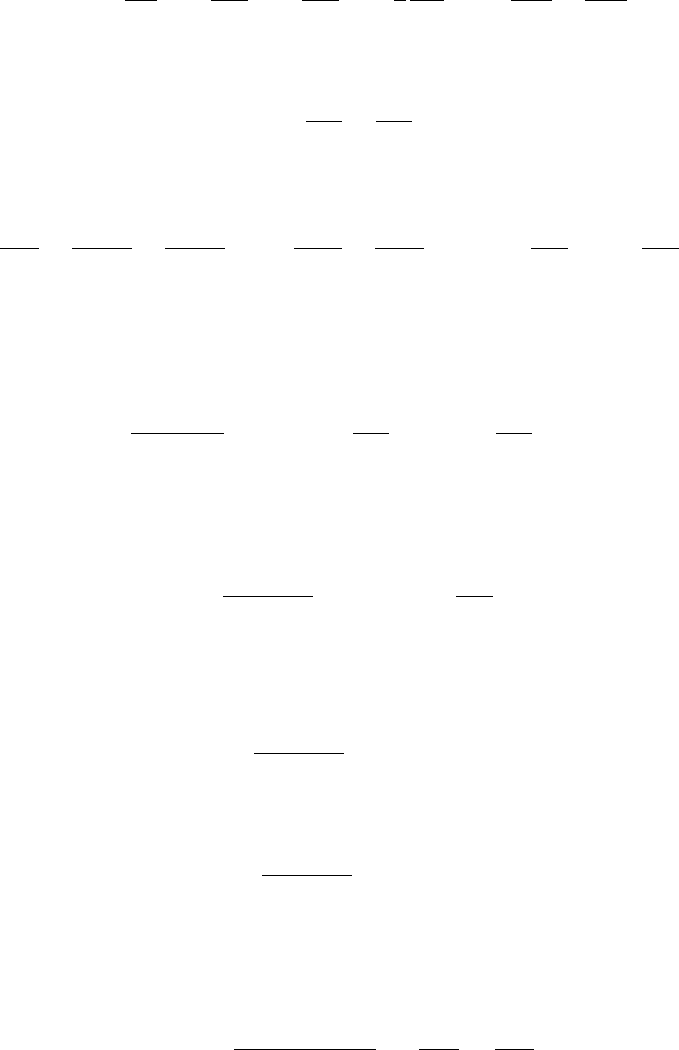
172 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

< ω

> в случае однородной и изотропной (в плоскости) двумерной турбулентности

в несжимаемой жидкости при нулевой скорости определенного течения. Кроме (6.14)

используем уравнение движения:

∂v

∂t

+ v

∂v

∂x

+ v

∂v

∂x

= −

∂p

∂x

+ ν

∂

∂x

∂

∂x

(6.15)

(i = 1, 2) и уравнение неразрывности:

∂v

∂x

∂v

∂x

= 0 . (6.16)

Умножая (6.14) на 2ω и проводя простые преобразования с учетом (6.16), получим:

∂ω

∂t

∂v

∂x

∂v

∂x

= ν

∂

∂x

∂

∂x

− 2ν





∂ω

∂x

∂ω

∂x





. (6.17)

Осредним это уравнение. Вследствие однородности турбулентности производные по ко-

ординатам от всех осредненных величин равны нулю. С учетом этого из (6.17) получа-

ется:

d < ω

= −2ν





*Ã

∂ω

∂x

*Ã

∂ω

∂x





. (6.18)

Из (6.15) после умножения на 2v

, суммирования полученных уравнений для i = 1, 2,

преобразований с учетом (6.16) и осреднения получается:

d < v

= 2 ν

i,k=1

*Ã

∂v

∂x

, (6.19)

где v

= v

+ v

. В случае изотропной турбулентности правая часть (6.19) равна 4ν <

>, так что справедливо уравнение

d < v

= −4ν < ω

> . (6.20)

Как видно из (6.18), величина < ω

> убывает со временем. Отсюда и из (6.20) следует,

что

d < v

≤ 4ν < ω

, (6.21)

где < ω

- начальное значение < ω

> (t). Если, в частности, в начальный момент

создать только крупные вихри с характерным размером `

и с характерной скоростью v

то порядок величины правой части в (6.21) будет νv

. При этом из (6.21) получается:

d(< v

> /v

)

d(tv

)

≤

. (6.22)

Если число Рейнольдса Re

достаточно велико, то, как видно из (6.22), турбулентность

получается почти не угасающей: за время одной пульсации `

относительная вели-

чина изменения < v

> / < v

> не превышает Re

−1

, т.е. является чрезвычайно малой.

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 173

Для сравнения напомним, что в случае трехмерной турбулентности диссипация энергии

оценивается формулой (6.8), в соответствии с которой промежуток времени τ , в тече-

ние которого угасание энергии турбулентности совпадает по порядку величины с самой

этой энергией, равен продолжительности одной крупномасштабной пульсации, так как

согласно (6.8)

ετ = ε`/v ≈ v

Проведенные оценки подтверждают для рассмотренного примера ранее сделанный вы-

вод об отсутствии для плоской турбулентности каскадного механизма переноса энергии

от крупных вихрей к мелким. Однако, отсюда, конечно, не следует, что в этом слу-

чае нелинейный механизм взаимодействия вихрей вообще не действует. В заключение

настоящего параграфа отметим еще раз, что в реальных турбулентных потоках круп-

ные вихри иногда могут быть близкими к "плоским", а мелкие вихри - трехмерными.

Особенности переноса энергии при такой турбулентности изучены еще очень мало.

6.4 Однородное изотропное турбулентное движение среды

Изучение турбулентности в однородном (т.е. имеющей одинаковые характеристики в

любой точке пространства) и изотропном (независимость турбулентных характеристик

от пространственной ориентации для любой группы точек) случае представляет инте-

рес по нескольким причинам. Во-первых, как указывалось в разделе 6.3, даже неодно-

родное в крупномасштабном движении турбулентное движение приближенно является

однородным и изотропным в мелкомасштабном. Во-вторых, вследствие существенного

упрощения применяемого математического аппарата, в теории однородной изотропной

турбулентности удается продвинуться существенно дальше, чем в других случаях. И, в-

третьих, наконец, теория однородной изотропной турбулентности часто является исход-

ной при построении приближенных методов расчета неоднородных или неизотропных

турбулентных потоков.

6.4.1 Корреляционные функции в однородной изотропной турбулентности

Рассмотрим вначале наиболее простой случай однородной изотропной турбулентности

в несжимаемой жидкости. Основными объектами исследования здесь будут корреляци-

онные функции различных величин. Определим корреляционную функцию скоростей,

являющуюся двухточечным моментом скоростей второго порядка:

(~x, ~r) =< v

(~x)v

(~x + ~r) > . (6.23)

В однородном случае в каждый фиксированный момент времени B

зависит только от

вектора ~r, определяющего относительное положение двух рассматриваемых точек M(~x)

M(~x + ~r). В однородной изотропной турбулентности B

(~x, ~r) = B

(r), т.е. зависит

только от расстояния между этими точками. Изотропность турбулентности означает,

что корреляционная функция скоростей B

не изменяется при поворотах и зеркальных

отображениях системы координат. Изотропный тензор B

(r) может быть представлен

в следующем общем виде:

(r) = C(r)

+ D (r)δ

. Здесь r

- проекция радиуса-вектора ~r на координатные оси, δ

- символ Кронеке-

ра. Это разложение следует из того, что существует только два изотропных тензора

174 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

второго ранга, которые можно составить из компонентов радиуса-вектора ~r - это r

и δ

. Из разложения B

следует, что 9 компонентов тензора B

определяются лишь

двумя функциями C(r) и D(r), вместо которых далее введем продольную и поперечную

корреляционные функции:

(r) =< v

(0)v

(~r) >,

(r) =< v

(0)v

(~r) >

рис.3.1

Индексы L и N указывают продольные и поперечные направления. Выразим функ-

ции C(r) и D(r) через продольную и поперечную корреляционные функции. Поскольку

турбулентность является изотропной, можно выбрать систему координат с осью x

, сов-

падающей с вектором

, тогда радиус-вектор будет иметь координаты ~r(r, 0, 0). Для

C(r) и D(r) получим соотношения

= C(r) + D(r), B

= D(r),

из которых следует разложение корреляционной функции

(r) = (B

− B

)

+ B

. (6.24)

Для несжимаемой жидкости функции B

и B

связаны еще одним соотношением,

которое получается из уравнения неразрывности:

∂B

∂r

=< v

(0)

∂v

(r)

∂r

>= 0.

Подставляя в это уравнение (6.24) и выполняя дифференцирование, получим

(r) =

1 +

(r). (6.25)

С помощью корреляционных функций можно определить масштабы турбулентности.

Интегральный масштаб турбулентности, примерно соответствующий размерам крупных

вихрей, определяется интегралом

L =

(0)

∞

(r)dr. (6.26)

Микромасштаб турбулентности, соответствующий мелким вихрям, определяется кри-

визной корреляционной функции

−

(0)

B”

(0)

1/2

. (6.27)

Можно ввести также другие корреляционные функции, примеры которых рассматри-

вались в разделе 6.3:

(~r) =< ∆v

∆v

>, ∆v

= v

(~r) − v

(0). (6.28)

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 175

Для однородной изотропной турбулентности эти функции связаны с B

соотношени-

ем, которое получается из сравнения определений B

, R

и условий однородности и

изотропности:

(r) = 2[B

(0) − B

(r)] (6.29)

и для них справедливы соотношения, аналогичные (6.24), (6.25). Рассмотрим теперь

некоторые свойства двухточечного момента третьего порядка

ij,l

(~x, ~r) =< v

(~x)v

(~x + ~r) > . (6.30)

В однородном изотропном случае этот тензор выражается через симметричные по i, j

тензоры третьего ранга r

, r

+ r

, r

и скалярные функции расстояния между

точками:

ij,l

(r) = B

(r)

+ B

(r)

+ δ

+ B

(r)

Выразим функции B

, B

через три следующих момента:

LL,L

(r) =< v

(0)v

(r) >,

NN,L

(r) =< v

(0)v

(r) >,

LN,N

(r) =< v

(0)v

(r).

Аналогично (6.25) получим:

ij,l

(r) = (B

LL,L

−B

NN,L

−2B

NN,L

−2B

LN,N

)

LN,N

+ δ

NN,L

. (6.31)

Используя следствие уравнения неразрывности ∂B

ij,l

/∂r

= 0, можно все компонен-

ты тензора B

ij,l

выразить через единственный двухточечный момент третьего порядка

LL,L

NN,L

= −(1/2)B

LL,L

, ; (6.32)

LN,N

= (1/ 2)[1 + (r/2)d/dr]B

LL,L

. (6.33)

Рассмотрим теперь корреляционную функцию скалярного и векторного полей в одно-

родной изотропной турбулентности несжимаемой жидкости:

(r) =< p(0)v

(r) >,

где p(r) - произвольное скалярное поле (давление, температура, концентрация пассивной

примеси). Единственный вектор, который можно образовать из компонентов радиуса-

вектора ~r, это сам вектор ~r, поэтому

(r) = B(r)r

/r.

Из уравнения неразрывности ∂B

/dr = 0 следует, что функция B(r) удовлетворяет

уравнению

R = 0,

которое с учетом ограниченности при r → 0 имеет нулевое решение. Отсюда следует, что

скалярное и векторное поля в однородной изотропной турбулентности не коррелируют

(r) ≡ 0).

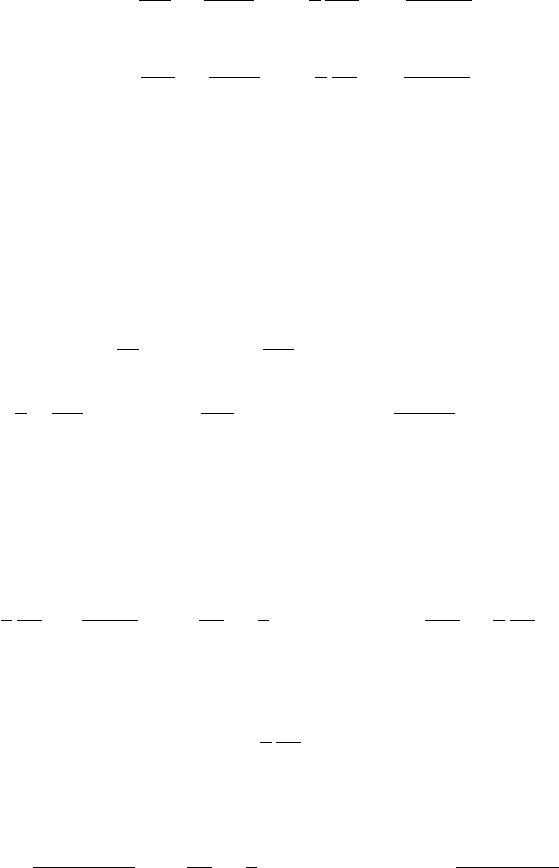
176 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

6.4.2 Уравнение Кармана-Ховарта

Таким образом, единственной независимой корреляционной функцией второго поряд-

ка является B

(r). Получим уравнение, которому она удовлетворяет. Очевидно, что

в однородном случае, не теряя общности, можно считать, что жидкость как целое не

движется, так как < v

>= 0, поэтому далее величинами v

, p будем обозначать пуль-

сации скорости и давления. Выберем две точки в жидкости M и

M, все параметры в

этих точках будем обозначать соответственно (x

, v

, p

) и (˜x

, ˜v

, ˜p

). Запишем уравнения

движения несжимаемой среды в этих точках, считая вязкость ν постоянной:

∂v

∂t

∂v

∂x

= −

∂p

∂x

+ ν

∂

∂x

, (6.34)

∂ ˜v

∂t

∂ ˜v

˜v

∂ ˜x

= −

∂ ˜p

˜x

+ ν

∂

˜v

∂ ˜x

. (6.35)

Умножим (6.34) на ˜v

, (6.35) на v

, осредним и перейдем к относительной координате

= ˜x

− x

. При этом преобразовании

∂/∂ ˜x

= ∂/∂r

∂/∂x

= −∂/∂r

В результате получим:

∂

∂t

< v

˜v

∂

∂r

(< v

˜v

> − < v

˜v

) + (6.36)

∂

∂r

< p ˜v

> −

∂

∂r

< v

˜p >

+ 2ν

∂

∂r

< v

˜v

> .

Подставляя для < v

˜v

> выражение (6.25) с учетом (6.28), для < v

> ˜v

> - ( 6.30) с

учетом (6.31), равенства B

i,jl

(r) = B

jl,i

(−r) и учитывая, что для изотропной турбулент-

ности < p ˜v

>=< v

˜p >= 0, получим следующее уравнение для продольной корреляци-

онной функции:

1 +

∂

∂r

!Ã

∂B

∂t

−

"Ã

∂

∂r

LL,L

+ 2ν

∂

∂r

∂

∂r

= 0 .

Единственным решением уравнения

1 +

∂

∂r

f(r) = 0,

не имеющим особенности при r = 0, является функция f(r) ≡ 0, поэтому получаем

∂B

(r, t)

∂t

∂

∂r

!Ã

LL,L

(r, t) + 2 ν

∂B

(r, t)

∂r

. (6.37)

Это уравнение носит наименование уравнения Кармана-Ховарта [44]. Уравнение (6.37)

связывает две неизвестные функции - второй и третий моменты скоростей, что является

проявлением обсуждавшейся в разделах 6.2, 6.3 незамкнутости уравнений для пульса-

ционных моментов. По этой причине решение уравнения Кармана-Ховарта может быть

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 177

получено лишь при некоторых гипотезах относительно B

LL,L

или на стадии вырождения

турбулентности, когда прекращается перераспределение энергии по спектру и турбу-

лентность затухает. Перераспределение энергии пульсационного движения происходит

вследствие нелинейного взаимодействия волн, которое описывается в уравнении (6.37)

членом B

LL,L

, поэтому на стадии распада турбулентности можно принять B

LL,L

= 0. В

этом случае уравнение Кармана-Ховарта становится замкнутым и его решение может

быть найдено в общем виде. Уравнение (6.37) можно переписать в следующем виде:

∂B

∂t

∂

∂r

LL,L

+ 2ν

∂B

∂r

. (6.38)

При B

LL,L

= 0 дифференциальный оператор в правой части совпадает с радиальной

частью оператора Лапласа в 5-мерном пространстве (для оператора Лапласа в п-мерном

пространстве радиальная часть

(∆

)

n−1

∂

∂r

!Ã

n−1

∂

∂r

Следовательно, уравнение (6.38) имеет вид уравнения теплопроводности в 5-мерном

пространстве, для которого функция Грина равна

(r, t) =

(8πνt)

5/2

exp

−

i=1

8νt

, (6.39)

где r

. Общее решение уравнения (6.38) имеет вид:

(r, t) =

(8πνt)

5/2

∞

−∞

...

∞

−∞

, 0) exp

−

i=1

− r

)

8νt

...dr

. (6.40)

На больших временах, когда t >> r

/ν , подинтегральное выражение в (6.40) не зависит

от времени, поэтому из (6.40) следует асимптотическое поведение продольной корреля-

ционной функции при t → ∞

(r, t) →

const

(8πνt)

5/2

. (6.41)

Из уравнения Кармана-Ховарта можно получить еще одно полезное соотношение. Умно-

жим (6.38) на r

и проинтегрируем по r :

max

(r)dr = r

max

LL,L

max

) + 2νr

max

∂B

∂r

max

Если B

(r) на больших расстояниях стремится к нулю быстрее r

−3

, а B

LL,L

быстрее

−4

, то интеграл в левой части сходится, и правая часть обращается в нуль, следова-

тельно, интеграл

Λ =

∞

(r, t)dr (6.42)

не зависит от времени. Интеграл (6.42) носит наименование инварианта Лойцянско-

го [43].

178 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

6.4.3 Спектральная форма корреляционных функций и уравнений

В однородной (но не обязательно изотропной) турбулентности часто используется спек-

тральное разложение корреляционных функций. Спектральное преобразование являет-

ся математической операцией, которое в некоторых случаях упрощает решение и про-

ясняет физический смысл результатов. Более подробное обсуждение смысла спектраль-

ного разложения моментов пульсирующих величин см., например, в [45]. Определим

преобразование Фурье для корреляционной функции в однородной турбулентности

(

k) =

−i

k·~r

(~r)d

r, (6.43)

(~r) =

−i

k·~r

(

(2π)

. (6.44)

Для изотропной турбулентности какое-либо выделенное направление отсутствует как в

координатном (~r) пространстве, так и в пространстве волновых чисел (

k), поэтому Φ

(

является изотропным тензором. Из компонентов вектора

k можно образовать только два

тензора второго ранга - k

и δ

, поэтому справедливо следующее разложение:

(

k) = C(k)

+ D (k)δ

. (6.45)

Спектральная форма неразрывности имеет вид

(~r)e

k·~r

= 0 ,

или

= 0 . (6.46)

Подставляя (6.45) в (6.46), находим связь между функциями C и D:

C(k) + D(k) = 0.

Определим спектральную плотность энергии турбулентности. Из (6.23) и (6.44) для

однородной турбулентности следует

< v

(0)v

(0) >=

2π)

(

k)d

k. (6.47)

Левая часть этого выражения равна кинетической энергии пульсационного движения,

поэтому (6.47) можно записать в виде

< v

∞

E(k)dk, (6.48)

где функция E(k) представляет кинетическую энергию, приходящуюся на интервал dk

волновых чисел и называется спектральной плотностью кинетической энергии турбу-

лентности. Подставляя разложение (6.45) в (6.47) с учетом связи функции C(k) и D(k) и

Здесь преобразование Фурье используется в форме, которая была принята в других разделах курса. Эта форма

отличается от используемой, например, в [32] наличием множителя (2π)

−3

в (6.43) и его отсутствием в (6.44).

6.4. ОДНОРОДНОЕ ИЗОТРОПНОЕ ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ СРЕДЫ 179

сравнивая с (6.48), получаем следующее выражение для Фурье-образа корреляционной

функции скоростей в однородной изотропной турбулентности:

(

k) =

2π

E(k)

−

. (6.49)

Следовательно, корреляционная функция Φ

(k) или B

(~r) в этом случае полностью

определяется спектральной плотностью энергии E(k) . Получим уравнение, которому

удовлетворяет корреляционная функция Φ

(

k). Имея в виду в дальнейшем более об-

щий случай, получим вначале уравнение для Φ

(

k) для однородной, но не обязательно

изотропной функции, а затем в частном случае расширим упрощения, возникающие

для изотропной турбулентности. Применим преобразование Фурье к уравнению (6.37),

при выводе которого использовалось лишь предположение об однородной турбулент-

ности, но изотропии не предполагалось. В результате преобразования Фурье, которое

формально получается заменами ∂/∂r

→ ik

и моментов их фурье-образами, получим

∂Φ

∂t

= A

(

k) + B

(

k) − 2νk

. (6.50)

Здесь введены следующие обозначения:

(

k) = ik

(< v

(0)v

(~r) >< v

(0)v

(~r)v

(~r) > e

−i

k·~r

r, (6.51)

(

k) =

< p (0)v

(~r) > k

< v

(0)p(~r) >)e

−i

k~r

r. (6.52)

Физический смысл уравнения (6.50) можно получить, взяв свертку этого уравнения

и умножив на k

/4π

, тогда с учетом ( 6.49), получим уравнение для спектральной

плотности энергии:

∂E(k)

∂t

= T (k) − 2νk

E(k), (6.53)

где

T (k) =

4π

(k) + B

(k)] . (6.54)

Уравнение (6.53) описывает изменение спектральной плотности энергии E(k) вследствие

воздействия различных факторов - диссипации под действием вязких сил и перераспре-

деление энергии по спектру вследствие тройных корреляций скорости (A

) и корреля-

ции давления и скорости (B

). Для того, чтобы показать, что A

и B

действительно

ответственны за перераспределение энергии пульсационного движения, исследуем их

свойства. Преобразуем выражение для B

, для этого возьмем дивергенцию уравне-

ния (6.34), умножим результат на ˜v

, осредним, перейдем к относительной координате

и применим преобразование Фурье. В результате получим:

< p ˜v

> e

−i

k·~r

r = −

< v

(0)v

(~r) e

−i

k·~r

r. (6.55)

Аналогично выражается корреляция < ˜pv

> через тройные корреляции скоростей. Под-

ставляя в (6.52), получим следующее выражение для B

(k) = i

< v

˜v

> −k

< v

˜v

>)e

−i

k·~r

r. (6.56)

180 ГЛАВА 6. ТУРБУЛЕНТНОЕ ДВИЖЕНИЕ ГАЗОВ, ЖИДКОСТЕЙ И ПЛАЗМЫ

Вследствие уравнения неразрывности (6.46) свертка B

равна нулю:

= 0 (6.57)

Этот результат подтверждает, что член B

описывает обмен энергией пульсационного

движения по различным осям вследствие корреляции скорости и давления. Исследу-

ем свойства тензора A

(

k). Из определения (6.51) и обратного преобразования Фурье

следует

(

k)d

r = lim

r→0

(

k)e

k·~r

r = lim

r→0

(~r). (6.58)

Вычислим предел, содержащийся в (6.58), используя (6.51:

(0) = lim

r→0

(~r) = lim

r→0

∂

∂r

< v

˜v

− ˜v

) >,

или, вычисляя далее, получим:

(0) = lim

r→0

< v

˜v

∂

∂r

− ˜v

) > + lim

r→0

< (v

− ˜v

)

∂

∂r

˜v

) >= 0.

Здесь использовано уравнение неразрывности в виде

∂v

∂r

∂ ˜v

∂r

= 0

и ограниченность величины ∂v

(~r)/∂r

. В результате получаем, что интеграл по спектру

тензора A

равен нулю:

(

k)d

k = 0, (6.59)

т.е. член A

в уравнении (6.50) ответствен за перераспределение энергии турбулентности

по спектру. Следствием уравнения (6.59) является равенство

∞

T (k)dk = 0, (6.60)

потому аналогичный смысл имеет и член T(k) в уравнении (6.53). Уравнение (6.50)

или (6.53) является спектральной формой уравнения Кармана-Ховарта, оно также яв-

ляется незамкнутым, так как содержит неизвестные третьи моменты A

, B

или T (k).

Для этого уравнения также существует проблема замыкания, поэтому решения это-

го уравнения могут быть получены только на стадии распада турбулентности, когда

= B

= 0, или при некоторых предложениях об этих членах, основанных на фи-

зических гипотезах о перераспределении энергии по координатным осям и по спектру.

Решение уравнения (6.53) на стадии вырождения турбулентности при T (k) = 0 имеет

вид

E(k) = E

(k)e

−2νk

, (6.61)

откуда следует, что в первую очередь происходит угасание мелких вихрей, соответству-

ющих большим значениям k. Спектральная плотность энергии E(k) имеет максимум

в области k ∼ `

−1

, т.е. основная доля кинетической энергии пульсационного движения

сосредоточена в крупных вихрях, эта область масштабов вихрей называется энергети-

ческим интервалом. Область волновых чисел k > r

−1

называется вязким интервалом,