Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.


5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 131
учета термодиффузии и электрического тока в тепловой поток получаем
q = −λ∇T +
X
α
h
α
i
α
. (5.68)
Это приближение называется приближением локального химического равновесия (ЛХР)
[7].
Частные случаи выражений для потоков
Однокомпонентный частично-ионизованный газ В этом случае газ состоит из атомов,
ионов и электронов (A, A
+
, e). Потоки тепла и плотность электрического тока имеют
вид
q = −λ∇T −
5
2
kT
e
j − β
µ
E
∗
+
∇
T
µ
e
e
¶
,
j = σ
"
µ
E
∗
+
∇
T
µ
e
e
¶
+ α
∇kT
e
#
.
Последнее выражение представляет закон Ома, из которого можно найти электрическое
поле:
E = −
1
c
v × H +
j
σ
−
1
e
∇
T
µ
e
− α∇T.
Проинтегрируем это соотношение вдоль некоторой линии, соединяющей произвольные
точки 1, 2 в потоке:
Z
2
1
E · dl = −
Z
2
1
1
c
(v × H) · dl +
Z
2
1
j
σ
· dl −
δ
T
µ
e
e
− αδT.
Химический потенциал электронов имеет вид
µ
e
= kT ln n
e
λ
3
e
,
δ
T
µ
e
e
=
kT
e
e
δn
e
n
e
.
Величина αδT = α(e/k)δkT
e
/e, где α(e/k) = α
0
' 1, поэтому это соотношение можно
записать в виде
δϕ
12
= E
инд
+ δϕ
омич
12
−
kT
e
e
δn
e
n
e
− α
0
δ
kT
e
e
.
При δn
e
∼ n
e
, обычно kT
e
/e ≤ δϕ
12
, поэтому последние члены несущественны и закон
Ома можно использовать в виде
j = σ
µ
E +
1
c
v × H
¶
. (5.69)
По этой же причине q ≈ −λ∇T , однако выполнение этих условий в конкретных задачах
необходимо проверять.
Двухкомпонентный частично-диссоциированный газ Газ состоит из молекул и атомов
(A
2
, A). Для упрощения предположим, что и ∇p = 0. Обозначим концентрацию атомов
c
A
≡ c , тогда концентрация молекул c
A
2
= 1−c. Двухкомпонентный газ характеризуется
одним коэффициентом диффузии, т.к. i
A
+ i
A
2
= 0. Обозначим i
A
≡ i, тогда i
A
2
= −i.
Диффузионный поток атомов в простейшем виде можно принять в виде
i = − ρD∇c.

132 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД
Преобразуем тепловой поток:
q = −λ∇T + i
1
h
1
+ i
2
h
2
= −λ∇T + i(h
1
− h
2
).
Дифференциал энтальпии равен:
dh = c
1
dh
1
+ c
2
dh
2
+ h
1
dc
1
+ h
2
dc
2
,
его градиент
∇h = c
pf
∇T + (h
1
− h
2
)∇c,
где "замороженная" теплопроводность c
pf
= c
1
c
p1
+ c
2
c
p2
. Переходя от градиента тем-
пературы к градиенту энтальпии, тепловой поток можно представить в виде
q = −
λ
c
pf
[∇h + (h
1
− h
2
)(L
e
− 1)∇c] ,
где Le = ρDc
pf
/λ
f
– число Льюиса. Таким образом, массовый поток и поток тепла
выражаются через градиенты энтальпии и концентрации атомов.
Неионизованная среда с двумя химическими элементами Рассмотрим пример водород-
кислородной смеси, состоящей из атомов и молекул, содержащих водород и кислород
(H
2
O, H
2
, O
2
, H, O) в модели ЛХР. Определим эффективную концентрацию химического
элемента – кислорода с
∗
≡ с
∗
O
в соответствии с (5.64):
с
∗
≡ с
∗
O
=
16
18
c
H
2
O
+ c
O
2
+ c
O
.
Выражая градиенты удельных химических потенциалов через градиенты давления и
концентрации:
∇
T
˜µ =
∂ ˜µ
∂p
∇p +
∂ ˜µ
∂c
∇c,
можно найти выражения для потока тепла и массового потока одного из химических
элементов:
q = −λ
эфф
∇T + λ
эфф
p
∇p + λ
эфф
c
∇c,
i = −ρD
эфф
(∇c + k
эфф
T
∇T + k
эфф
p
∇p),
где λ
эфф
, λ
эфф
p
, λ
эфф
c
, D
эфф
, k
эфф
T
, k
эфф
p
– эффективные коэффициенты теплопроводности,
диффузии, термо- и бародиффузии. Детальные выражения для них предлагается найти
самостоятельно.
Аналогично можно получить выражения для потоков тепла и массы в других слу-
чаях, например, для частично-ионизованной и частично-диссоциированной среды и т.д.
5.6.2 Магнитогидродинамическое приближение
Рассмотрим проводящую среду. Существенное отличие описания проводящей от непро-
водящей среды имеется в уравнении движения, где добавляется электромагнитная сила,
в балансе энергии добавляется джоулево выделение тепла j · E
∗
, в систему уравнений
необходимо включить систему уравнений Максвелла и замыкающие выражения для по-
токов (в случае проводящей среды это закон Ома и другие потоки).

5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 133
Уравнение движения имеет вид (5.37):
ρ
"
∂v
∂t
+ (v · ∇)v
#
= −∇p + ∇ · σ + ρ
∗
e
E
∗
+
1
c
j × H. (5.70)
Уравнения Максвелла были приведены ранее (5.13), (5.14), (5.15), (5.16). Предполагает-
ся, что кроме электромагнитных, объемных сил нет. Повторяя рассуждения по упроще-
нию закона Ома, полученном ранее (5.69), при условиях δn
e
∼ n
e
и δkT
e
/e ¿ δφ
12
можно
закон Ома использовать в виде (5.69), который справедлив при следующих условиях:
1. Электропроводность σ не зависит от магнитного поля. Движение заряженных ча-
стиц происходит по спирали с ларморовским радиусом. Если ларморовский радиус
много больше длины свободного пробега, т.е. r
L
À l, то, учитывая, что средний
ларморовский радиус равен r
L
∼ v
T
/ω (ω = eH/mc – циклотронная частота элек-
тронов, v
T
– тепловая скорость), средняя длина свободного пробега l ∼ v
T
/ν, при-
веденное неравенство сводится к малости параметра Холла: l
e
/r
L
∼ ( v
T
/ν)(ω/v
T
) ∼
(ω/ν) = ωτ ¿ 1.
2. Характерное время изменения параметров должно превышать время восстанов-
ления электронейтральности τ À τ
p
. Рассмотрим задачу o колебаниях зарядов в
объеме, ограниченном мысленно выделенными стенками. При смещении зарядов на
границах возникает положительный и отрицательный поверхностный заряды, что
приводит к возникновению электрического поля E = 4πσ, где σ = en
e
xS/S = en
e
x –
поверхностная плотность заряда. С учетом этого, получаем E = 4πen
e
x. Уравнение
движения зарядов имеет вид
m¨x = −4πe
2
n
e
x, или ¨x + ω
2
p
x = 0,
где
ω
p
=
q
4πn
e
e
2
/m − плазменная частота. (5.71)
Строгий вывод основан на решении системы уравнений непрерывности заряда, определения плотности
электрического тока, дрейфового движения электронов и уравнения Пуассона:
∂ρ
∗
e
∂t
= −∇ · j, j = −n
e
ev, m
∂v
∂t
= eE − ν
m
v, ∇ · E = 4πρ
∗
e
.
Для плотности объемного заряда получается волновое уравнение с частотой распространения колебаний
ω
p
:
∂
2
ρ
∗
e
∂
2
t
+ ω
2
ρ
∆ρ
∗
e
= 0.
Чем выше n
e
, тем больше ω
p
, поэтому условие τ À τ
p
необходимо в первую очередь
проверить для малых n
e
. В практических единицах
ω
p
=
s
4πn
e
e
2
m
= 56 .42 · 10
3
√
n
e
(Гц),
где n
e
в см
−3
. При n
e
= 10
10
см
−3
, ω
p
= 5.6 · 10
9
c
−1
, т.е. вышеприведенное условие
является необременительным.
3. v
др
¿ v
T
. При каждом столкновении электрон теряет энергию
∆ε =
m(v + v
T
)
2
2
−
(mv
T
)
2
2
= mv
др
v
T
= 2
v
др
v
T
ε.
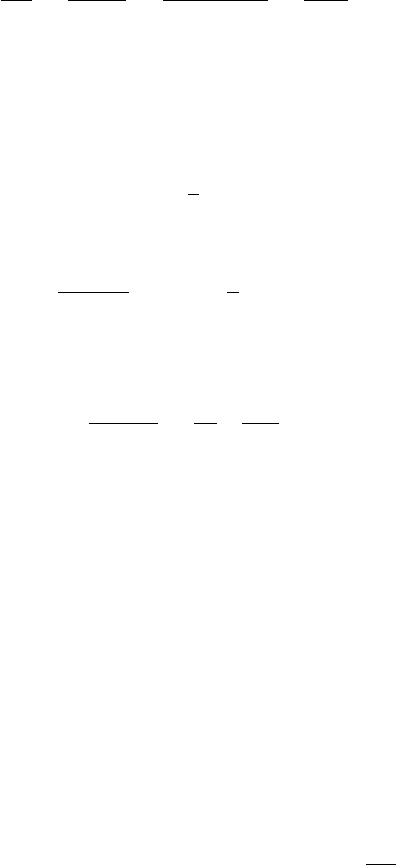
134 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД
Если v
др
∼ v
T
, то ∆ε ∼ ε. Сечение рассеяния Q
lε
∼ 1/v
n
∼ 1/ε
n/2
, поэтому вероят-
ность столкновений с ростом энергии уменьшается. Возникает убегание электронов,
не испытавших столкновений, что приводит к изменению закона Ома и возникно-
вению пробоя. Отношение дрейфовой к тепловой скорости электронов может быть
выражено через известные параметры:
v
др
v
T
'
eE
mνv
T
=
eE
mNv
T
σv
T
'
eEλ
T
¿ 1, (5.72)
где eEλ/kT ∼ E/p ∼ E/N, – параметр, используемый в физике газового разряда.
Оценим величину возможного отрыва электронной и газовой температур. В отсут-
ствие отрыва параметр (T
e
−T )/T ¿ 1. Баланс энергии электронов в электрическом
поле имеет вид
σE
2
− n
e
ν
m
δ
3
2
k(T
e
− T ) = 0,
откуда находим
n
e
e
2
E
2
mν
m
= n
e
ν
m
δ
3
2
k(T
e
− T ).
Из этого выражения следует величина отрыва температур:
T
e
− T
T
e
=
2
9δ
Ã
eEl
kT
e
!
2
, (5.73)
где l = 1/NQ
m
– длина свободного пробега электронов. Отрыв температур мал,
если энергия, набираемая электроном в электрическом поле на длине свободного
пробега мала по сравнению с их средней кинетической энергией.
4. Параметры, определяемые проводимостью среды. Размерность проводимо-
сти следует из формулы σ = n
e
e
2
/(mν
m
), откуда 4πσ = ω
2
p
/ν
m
. Предположим, что
проводимость достаточно велика, так что
4πστ À 1, (5.74)
где τ – характерное гидродинамическое время. Это соотношение можно предста-
вить в виде условия на характерное гидродинамическое время τ À ν
m
/ω
2
p
. Это
условие является условием на концентрацию электронов и гидродинамическое вре-
мя:
n
e
τ À 56.5(N/N
0
)(Q
m
/10
−18
см
2
)
q
T
эв
,
где N
0
= 3 · 10
19
см
−3
. Характерные значения τ ∼ L/v ∼ 10
−4
, т.е. n
e
À 10
6
см
−3
.
Таким образом, (5.74) обычно выполняется с запасом. При меньших концентраци-
ях электронов мала проводимость среды, следовательно, мала и электромагнитная
сила c
−1
j × H и мал джоулев нагрев σE
2
. Условие (5.74) нарушается в быстропе-
ременных полях, например, возникающих в плазме при распространении электро-
магнитных волн в ионосфере. При выполнении приведенного условия возникают
упрощения, приведенные ниже.

5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 135
Упрощения в магнитной гидродинамике
1. Оценим вклад тока смещения по отношению к току проводимости:
j
см
4πj
∼
∂E/∂t
4πσE
∼
1
4πστ
¿ 1.
2. Оценим вклад конвективного тока ρ
∗
e
v по отношению к току проводимости, где
объемный заряд оценим из уравнения Пуассона ∇ · E = 4πρ
∗
e
, откуда следует ρ
∗
e
∼
E/(4πL). В результате получаем
j
конв
j
∼
ρ
∗
e
v
σE
∼
E
4πL
v
σE
∼
1
4πστ
¿ 1.
3. Оценим вклад силы, связанной с объемным зарядом:
ρ
∗
e
E
jH/c
∼
E
4πL
cE
σEH
=
cE
4πσLH
∼
1
4πστ
¿ 1.
Характерные электрические поля при заданных магнитных определяются по вели-
чине ЭДС, возникающей при запирании тока E
max
∼ vH/c:
j = σ(E +
1
c
v × H) = 0.
Следовательно, при выполнении условия (5.74) можно не учитывать тока смещения
и конвективного тока, а также силы, связанной с объемным зарядом.
Уравнения МГД приближения
Электромагнитная сила может быть преобразована следующим образом:
F
M
=
1
с
j × H =
1
4π
(∇ × H) × H = −∇
H
2
8π
+
1
4π
(H · ∇)H.
Подставляя в уравнение движения, получим
ρ
"
∂v
∂t
+ (v · ∇)v
#
= −∇
Ã
p +
H
2
8π
!
+ ∇ · σ +
1
4π
(H · ∇)H. (5.75)
В уравнение движения входит магнитное поле, поэтому для него нужно получить за-
мкнутое уравнение. Для упрощения будем считать проводимость среды постоянной
(σ = const). Уравнения Максвелла при выполнении условия (5.74) имеют вид:
∇ × H =
4π
c
j, ∇ · H = 0,
∇ × E = −
1
c
∂H
∂t
, j = σ(E +
1
c
v × H).
Из уравнения электромагнитной индукции Фарадея следует:
∂H
∂t
= −c∇ × E = −c∇ × (
j
σ
−
1
c
v × H) = ∇ × v × H −
c
2
4πσ
∇ × ∇ × H.
136 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД
Двойное векторное произведение преобразуется следующим образом:
∇ × v × H = ∇
v
× v × H + ∇
H
× v × H = (H · ∇)v − H(∇ · v) + v(∇· H) − (v · ∇)H.
∇ × ∇ × H = ∇(∇ · H) − (∇ · ∇)H = −∆H.
В результате получаем
∂H
∂t
= ν
m
H + ∇ × v × H,
или
∂H
∂t
+ (v · ∇)H = ν
m
∆H + (H · ∇) v − H(∇ · v).
Джоулев нагрев
j · E
∗
=
j
2
σ
=
c
2
16π
2
σ
(∇ × H)
2
=
ν
m
4π
(∇ × H)
2
.
Система уравнений в МГД-приближении имеет вид
∂ρ
∂t
+ ∇ · ρv = 0, (5.76)
ρ
"
∂v
∂t
+ (v · ∇) v
#
= −∇
Ã
p +
H
2
8π
!
+ ∇ · σ +
Ã
H
4π
· ∇
!
H, (5.77)
ρT (
∂s
∂t
+ v · ∇s) = σ : ∇v − ∇ · q +
ν
m
4π
(∇ × H)
2
, (5.78)
∂H
∂t
+ (v · ∇)H = ν
m
∆H + (H · ∇)v − H(∇ · v), (5.79)
p = ρRT. (5.80)
5.6.3 Критерии подобия в магнитной гидродинамике
При больших магнитных числах Рейнольдса Re
m
À 1 проводимость бесконечна, по-
этому появляется только один параметр, связанный с магнитным полем, в качестве
которого можно выбрать число Альфвена, равное отношению скорости альфвеновских
и звуковых волн A = c
A
/a = (H
2
/4πρa) или параметр равный отношению газового и
магнитного давлений β = 8πp/H
2
.
При малых магнитных числах Рейнольдса Re
m
< 1, размерных параметров два –
электропроводность σ и магнитное поле, поэтому возникают динамические критерии:
Число Стюарта, равное отношению магнитных к инерционным силам
St =
|j × H|l
cρv
2
=
σH
2
l
c
2
ρv
,
Квадрат числа Гартмана равен отношению магнитных сил к вязким
Ha
2
=
1
c
|j × H|
∇σ
=
σH
2
c
2
ρv
.
Отметим связь между параметрами: St/Ha
2
= Re. Кроме этого вводятся параметры
Pr
m
= ν/ν
m
– магнитное число Прандтля, Lu = aL/ν
m
– число Лундквиста, где a –
скорость звука в газе.

5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 137
Принцип Фейнмана: одинаковые уравнения – одинаковое движение
Магнитогидродинамическое приближение имеет два аспекта.
• Магнитное поле оказывает силовое воздействие на проводящую среду.
• При движении проводящей среды возникают токи, которые создают индуцирован-
ное магнитное поле.
Задачи МГД являются линейными в двух случаях – либо когда внешнее магнитное по-
ле существенно превышает индуцированное, либо в том случае, когда индуцированное
поле имеет такое направление, при котором это поле не влияет на движение жидко-
сти. В этом случае надобность в уравнении магнитной индукции отпадает. Величина
индукционного магнитного поля определяется соотношением источников в уравнении
магнитной индукции.
|∇ × v × H |
|ν
m
δH|
∼
vL
ν
m
=
4πσvL
c
2
=
ω
2
p
ν
vL
c
2
=
ω
p
ν
v
c
ω
p
L
c
.
Re
m
= vL/ν
m
= 4 πσvL/c
2
– магнитное число Рейнольдса, оно характеризует отношение
индуцированного магнитного поля h к внешнему магнитному полю H
0
(H = H
0
+ h).
Уравнение магнитной индукции в несжимаемой среде имеет вид
dh
dt
= ν
m
∆h + (H
0
· ∇)v.
В стационарном состоянии h/H
0
∼ vL/ν
m
∼ Re
m
. При Re
m
¿ 1 индуцированное маг-
нитное поле много меньше внешнего h ¿ H
0
.
В этом разделе мы продемонстрируем принцип Фейнмана [22], заключающийся в
подобии движений, описываемых одинаковыми уравнениями. В МГД – приближении
магнитное поле удовлетворяет системе уравнений соленоидальности магнитного поля и
уравнению магнитной индукции:
∇ · H = 0, (5.81)
∂H
∂t
= ν
m
∆H + ∇ × v × H, (5.82)
или в другой форме
∂H
∂t
+ (v · ∇)H = ν
m
∆H + (H · ∇)v − H(∇ · v). (5.83)
Проведем аналогию с движением жидкости. Уравнение движения жидкости (Навье-
Стокса) имеет вид
∂v
∂t
+ (v · ∇)v = −
1
ρ
∇p + ν∆v. (5.84)
Пусть движение баротропно, т.е. ρ = f(p), тогда ∇p/ρ = ∇π. Применим к уравнению
(5.84) операцию ротора:
∂
∂t
(∇ × v) = ν∆(∇ × v) − ∇ × (v · ∇)v.

138 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД
Определим завихренность Ω = ∇ × v и преобразуем двойное векторное произведение
∇ × v × Ω = ∇ × (v × ∇ × v) = ∇ ×
Ã
∇
v
2
2
− (v · ∇)v
!
= −∇ × (v · ∇) v.
Следовательно, для завихренности получаем уравнение
∂Ω
∂t
= ν∆Ω + ∇ × v × Ω. (5.85)
Дивергенция завихренности
∇ · Ω = ∇ · (∇ × v) = 0. (5.86)
Сравним уравнения (5.82) и (5.85), а также (5.15) и (5.86). Из одинаковости уравне-
ний следуют одинаковые свойства, поэтому для изучения свойств уравнения магнитной
индукции можно использовать свойства уравнения для завихренности. В обоих случа-
ях движение среды различно для двух случаев – больших и малых магнитных чисел
Рейнольдса и, соответственно, больших и малых чисел Рейнольдса для жидкости.
Первый случай соответствует идеальной жидкости, поэтому напомним основные
уравнения и теоремы кинематики и динамики идеальной жидкости.
Кинематика идеальной жидкости
Введем понятие о трубке тока. Проведем в жидкости замкнутый контур и через каждую
точку проведем линию тока. Совокупность линий тока является поверхностью трубки,
а жидкость внутри – трубкой тока. Рассмотрим две точки, находящиеся на расстоянии
δr. Разность скоростей в точках равна δv = (δr · ∇)v. Перепишем это соотношение в
виде
(δr · ∇)v = δv = (∇v)
A
· δr + (∇v)
S
· δr,
получаем, что (∇v)
A
· δr = Ω × δr, где (∇v)
S
· δr – тензор деформаций.
ω =
1
2
∇ × v · δv = (δr · ∇)v = S · δr −
1
2
Ω × δr.
Отсюда следует первая теорема Гельмгольца: движение элементарного объема среды
разлагается на поступательное, вращательное и деформационное.
Введем понятие о вихревой трубке. Проведем в жидкости некоторый контур и через
его точки проведем вихревые линии, часть жидкости внутри этой поверхности обра-
зует вихревую трубку. Сформулируем вторую теорема Гельмгольца. Вычислим поток
завихренности через замкнутый контур
W
W’
Vdt
M
M
1
M’
M ’
1
e W
Рис. 5.2: Смещение вектора завихренности
в потоке
I
Ω · dA =
Z
∇ · ΩdV =
Z
∇ · (∇ × v)dV = 0,
следовательно, сохраняется поток завихренно-
сти через замкнутый контур
Z
Ω · dA = const.
Поток завихренности через поверхность может
быть выражен через циркуляцию скорости:
Z
Ω · dA =
Z
(∇ × v) · dA =
I
v · dr.
5.6. ГИДРОДИНАМИЧЕСКИЕ МОДЕЛИ 139
Ускорение жидкой частицы можно представить в виде
dv
dt
=
∂v
∂t
+ (v · ∇)v,
где первый член в правой части выражает нестационарность, а второй – неоднородность,
определяющую движение жидкой частицы.
Покажем, что имеет место теорема Кельвина:
d
dt
I
v · δr =
I
˙
v · δr.
Доказательство состоит в вычислении изменения по времени циркуляции вдоль линии
жидкой частицы:
d
dt
Z
B
A
v · δr =
Z
B
A
˙
v · δr +
Z
B
A
v · δv =
Z
B
A
˙
v · δr +
1
2
(v
2
B
− v
2
A
).
При совпадении точек А и В получаем теорему Кельвина.
Динамика идеальной жидкости
Выше было доказано, что Ω ×v = ( v ·∇)v −∇(v
2
/2), поэтому уравнение движения для
баротропной среды можно записать в форме Громека-Лэмба:
∂v
∂t
+ Ω × v = −∇
Ã
v
2
2
+ π
!
или в форме (5.85):
∂Ω
∂t
= ν∆Ω + ∇ × v × Ω.
Преобразуя двойное векторное произведение
∇ × v × Ω = (∇ · Ω)v + (Ω · ∇)v − (v · ∇)Ω − Ω(∇ · v),
для завихренности получаем уравнение, совпадающее со второй формой уравнения маг-
нитной индукции:
dΩ
dt
=
∂Ω
∂t
+ (v · ∇)Ω = (Ω · ∇)v − Ω(∇ · v). (5.87)
Первые члены в правой части уравнений для завихренности и магнитного поля
(Ω · ∇)v = Ω · (∇v) = Ω · S − Ω · Ω/2 = Ω · S
выражают эффекты деформации вектора Ω(H) скоростным полем, а член Ω(∇ · v)
определяет влияние сжимаемости среды.
Идеальная несжимаемая жидкость
В динамике идеальной несжимаемой жидкости имеет место уравнение Гельмгольца:
dΩ
dt
= ( Ω · ∇)v,
140 ГЛАВА 5. ГИДРОДИНАМИКА ВЫСОКОТЕМПЕРАТУРНЫХ СРЕД
имеющее результатом сохранение вихревых линий. В динамике сжимаемой жидкости
это уравнение имеет вид, который следует из уравнения (5.85) и уравнения непрерыв-
ности:
d
dt
Ω
ρ
=
Ã
Ω
ρ
· ∇
!
v.
dl
v
v+ d v
Рис. 5.3: Смещение элемента длины в
потоке
Получим уравнение для элемента длины жидкой
линии
δv = (δl · ∇)v,
но по определению
dδl
dt
= δv, (5.88)
поэтому δl удовлетворяет уравнению Гельмгольца
даже в сжимаемой жидкости. В несжимаемой жидкости δl = const, следовательно, и
Ω/ρ ∼ δl.
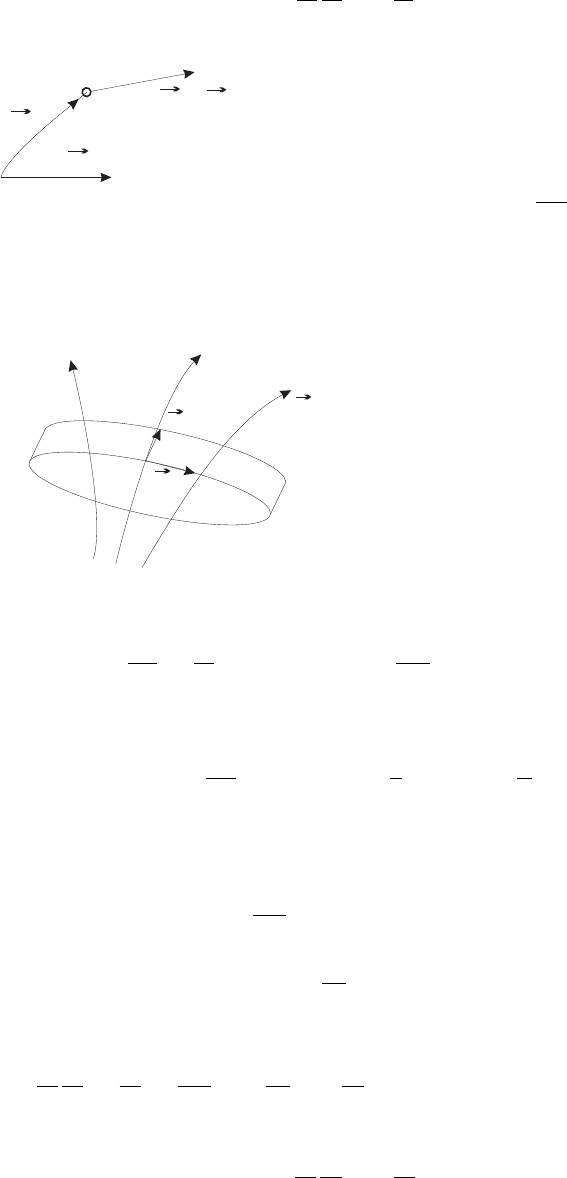
dr
vdt
H
Рис. 5.4: Сохранение потока магнитного поля
Рассмотрим движение проводящей
жидкости при Re
m
À 1. Докажем теоре-
му, аналогичную теореме Гельмгольца о
сохранении потока.
Z
H · dA = const,
Выделим жидкий контур и рассмот-
рим его положения в момент t и t + dt
Поток магнитного поля пересекает осно-
вания и боковую поверхность:
dΦ
dt
=
d
dt
Z
S(t)
H · dA =
Z
∂H
∂t
· dA +
I
H · (v × dl ).
Заменяя ∂H/∂t = −с∇ × E, получим
dΦ
dt
= −с
I
µ
E +
1
c
v × H
¶
=
j
σ
= 0.
Рассмотрим приближение вмороженного поля. Уравнения магнитной индукции и
непрерывности сжимаемого газа имеют вид
dH
dt
= (H · ∇)v − H (∇ · v),
dρ
dt
= −ρ∇ · v.
Найдем производную отношения
d
dt
H
ρ
=
1
ρ
2
Ã
ρ
dH
dt
− H
dρ
dt
!
=
1
ρ
2
[ρ(H · ∇)v − ρH(∇ · v) + ρH(∇ · v)],
или
d
dt
H
ρ
=
Ã
H
ρ
· ∇
!
v,
