Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

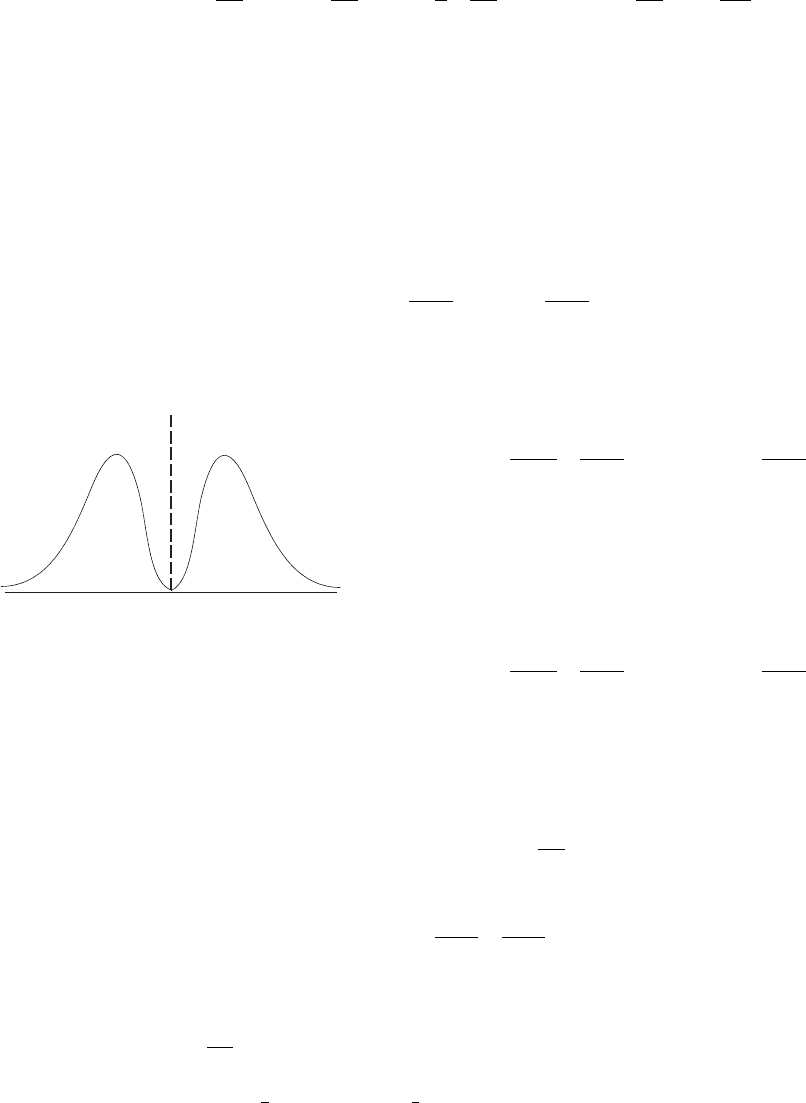
4.4. ИЗЛУЧЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ В ПЛАЗМЕ 101

Это уравнение определяет распределение ионов по радиусу r от излучающего атома.

Каждому данному значению r соответствует электрическое поле E, равное E = Ze/r

Поэтому, полагая в этом распределении r = (Ze/E)

1/2

, получаем функцию распределе-

ния микрополей в плазме:

dP (E) = exp

−

3/2

5/2

exp

−

3/2

, (4.45)

где E

= Ze/r

. Знак функции плотности вероятностей учитывает правильную норми-

ровку по E, а не по E

/E:

∞

E=0

dP (E) = 1.

В случае линейного эффекта Штарка ∆ω = s

E (это соответствует уширению уровня

¯h∆ω = αE, где α = s

¯h – поляризуемость состояния). Полагая ∆ ω

= s

, получим

функцию распределения по частотам:

dP (∆ω) = exp

−

∆ω

3/2

∆ω

3/2

. (4.46)

Основное предположение статистической теории состоит в том, что dP (∆ω) = a(∆ω)d∆ω.

Поэтому функция распределения линии имеет вид

Рис. 4.11: Форма спектральной линии для

штарковского уширения

a(∆ω) =

2∆ω

∆ω

3/2

exp

−

∆ω

3/2

Эта функция является двугорбой, она пред-

ставлена на рис. 4.11.

Для квадратичного эффекта Штарка ∆ω =

получаем

a(∆ω) =

4∆ω

∆ω

3/4

exp

−

∆ω

3/4

Электрическое поле E определяется векторной суммой электрических полей, создавае-

мых различными ионами E = |

|, поэтому рассмотрение, аналогичное предыдуще-

му, должно быть проведено в 3N-мерном пространстве. Это приводит к результату:

dP (E) = W (β)dβ, β =

соответственно

a(∆ω) = W

∆ω

где функция

W (β) =

3π

1 − 0.463β

+ 0.1227β

− ···

, при β ¿ 1 (4.47)

W (β) = 1.496β

−

1 + 5.107β

−

+ 14.93β

−3

+ ···

при β À 1. (4.48)

102 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

0.1

0.2

0.3

0.4

0.5

Рис. 4.12: Функция Хольцмарка

Функция Хольцмарка W (β) приведе-

на на рис. 4.12. Предельное поведение

формул (4.47) и (4.48) почти одинаковы.

Отличия состоят в определении электри-

ческого поля E

= Ze

πn

2/3

= 2.60eZn

2/3

и E

= 2.61eZn

2/3

. Если учесть эффекты

экранирования (на расстояниях выше де-

баевских ионы не создают электрических

полей), т.е. E = Ze

/r при r < D и E = 0 при r ≥ D, то форма линии начинает за-

висеть от N

= (4 /3)πD

n – числа ионов в дебаевской сфере. При D → ∞ получается

результат Хольцмарка. В плазме существует еще один эффект из-за взаимодействия

частиц – исчезновение спектральных линий для переходов между верхними энергетиче-

скими состояниями вследствие эффекта Инглиса-Теллера (см. раздел по ограничению

статистических сумм атомов).

4.4.7 Коэффициенты поглощения и испускания в спектральных линиях

При излучательном переходе из состояния 1 в состояние 2 в единицу телесного угла из

единицы объема в единицу времени излучается энергия:

¯hω

4π

Из соотношений Кирхгофа коэффициент поглощения определяется выражением: κ

. Для нахождения коэффициента поглощения составим уравнение для интенсив-

ности излучения

SdI

= −SI

(σ

− σ

)dx + ε

Sdx,

или

= −κ

+ ε

где

= N

− N

= N

1 − e

−¯hω/kT

где κ = κ

(1 − exp(−¯hω/kT )) – коэффициент поглощения, а "истинный" коэффициент

поглощения определяется формулой

= n

Коэффициент усиления лазера определяется аналогично коэффициенту поглоще-

ния:

α = N

−

4.5. УРАВНЕНИЕ ПЕРЕНОСА ИЗЛУЧЕНИЯ 103

4.5 Уравнение переноса излучения

Получим уравнение переноса излучения, используя кинетическое уравнение для фото-

нов, т.е. уравнение для числа фотонов f

в фазовом пространстве (r, p

), где p

= n¯hω/c

– импульс фотона, n – единичный вектор в направлении распространения фотона с им-

пульсом p. Концентрация фотонов в координатном пространстве определяется выраже-

нием

= 2 f

(2π¯h)

4π

dω

do. (4.49)

Множитель "2" учитывает два направления поляризации фотона. Кинетическое урав-

нение для фотонов имеет вид, аналогичный кинетическому уравнению для частиц, за

исключением силы, действующей на фотоны:

∂f

∂t

+ cn · ∇f

= St[f

]. (4.50)

Правая часть уравнения описывает изменение числа фотонов, которое обусловлено по-

глощением и испусканием фотонов. Так, для состояний a и b, принадлежащих дискрет-

ному или непрерывному спектрам, этот член имеет следующий вид:

St[f

] = c

a,b

[−N

+ N

(1 + f

)] − cN

+ (4.51)

K(nn

, ω, ω

dω

Последние два члена учитывают эффекты рассеяния и в дальнейшем учитываться не

будут. σ

– сечение томсоновского рассеяния, имеющее порядок πr

, где r

– классиче-

ский радиус электрона. Предполагая распределение частиц больцмановским и принимая

во внимание принцип детального баланса, получим

St[f

] = c

1 − e

−¯hω/kT

(0)

− f

где

(0)

¯hω/kT

− 1

– функция Планка распределения фотонов по частотам в состоянии термодинамическо-

го равновесия. В отсутствии рассеяния фотонов уравнение для функции распределения

фотонов или кинетическое уравнение для фотонов получаем в следующем виде:

∂f

∂t

+ n · ∇f

= κ

(0)

− f

). (4.52)

Первый член в левой части мал по порядку отношений скорости тепловой частиц к

скорости света v

/c ¿ 1 , поэтому уравнение для f

приобретает вид:

n · ∇f

= κ

(0)

− f

). (4.53)

Интенсивность излучения связана с функцией распределения фотонов соотношением,

которое следует из определения интенсивности как потока энергии фотонов в направ-

лении их распространения:

dωdo = c¯hωdn

= f

¯hω

4π

dωdo,

104 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

откуда следует

¯hω

4π

Умножая уравнение (4.53) на ¯hω

/4π

, получаем уравнение переноса излучения:

n · ∇I

= κ

− I

), (4.54)

где интенсивность излучения черного тела:

¯hω

4π

(0)

¯hω

4π

¯hω/kT

− 1

. (4.55)

Это выражение можно получить и феноменологически, рассматривая как и ранее, ослаб-

ление интенсивности на длине dx:

SdI

= −κ

dxI

S + ε

Sdx.

C учетом закона Кирхгофа получаем уравнение переноса излучения (4.54). Недостаток

феноменологического вывода в том, что в нем не определяются коэффициент поглоще-

ния κ

и выражение для интенсивности излучения черного тела B

4.5.1 Решение уравнения переноса излучения

Рассмотрим задачу, в которой имеется полупространство, заполненное средой. Пусть

слева на границу полупространства падает излучение интенсивности I

. Требуется опре-

делить интенсивность излучения в точке с координатой s. Эта задача может быть реше-

на чисто математически, но представляет интерес получить физический вывод решения

этого уравнения. Решение поставленной задачи сразу может быть записано в виде, ко-

торый следует из рис. 4.13:

)0(

s’’

s’

Рис. 4.13: Распространение излучения в среде

(s) = I

(0)

exp

−

)ds

) exp

−

)ds

. (4.56)

Здесь первый член представляет часть падающего излучения, которое дошло до точки s,

его ослабление определяется экспонентой exp (−

)ds

). Второй член определяется

излучением, которое возникло в точке s

с учетом закона Кирхгофа и которое затем

частично поглощено на длине s − s

4.5.2 Излучение плоского слоя

Решим задачу об излучении плоского слоя с постоянной температурой. Рассмотрим слу-

чай, когда имеется плоский слой, имеющий постоянную температуру. Требуется найти

угловое распределение интенсивности на частоте ω (рис. 4.14).

4.5. УРАВНЕНИЕ ПЕРЕНОСА ИЗЛУЧЕНИЯ 105

)(J

Рис. 4.14: Излучение плоского слоя

Это распределение интенсивности опреде-

ляется вторым членом общего решения. По-

сле замены переменных s = x/ cos ϑ и ds =

dx/ cos ϑ, решение имеет вид

(ϑ) =

x=0

exp

−

l/ cos ϑ

x/ cos ϑ

(s)ds

cos ϑ

Интегрирование приводит к результату:

(ϑ) = B

1 − e

−κ

l/ cos ϑ

В предельном случае при ϑ → 0 получаем

(0) = B

а при ϑ → π/2, I

→ B

, т.е. под малыми углами ϑ слой излучает как тонкое тело, а

под большими – как черное. Интенсивность излучения I

(ϑ) необходима для учета излу-

чения в уравнении энергии в гидродинамике, куда входит дивергенция радиационного

потока ∇ · q

. Радиационный поток q

определяется по формуле:

∞

dω,

где q

– спектральная плотность радиационного потока, определяющаяся интенсивно-

стью излучения:

do,

где n – единичный вектор, направленный по лучу, вдоль которого интенсивность излу-

чения равна I

(ϑ, φ).

÷åðíîå

òåëî

Рис. 4.15: Радиационный поток излучения

от черного тела в полупространство

В качестве примера найдем радиационный

поток излучения от черного тела в полупро-

странство:

do.

В направлении оси x излучается радиационный

поток

π/2

ϑ=0

cos ϑB

2π sin ϑdϑ = πB

Найдем интегральный поток по частотам:

dω = π

∞

dω.

Получаем

¯hω

4π

∞

¯hω/kT

− 1

dω,

или в безразмерном виде:

4π

¯h

∞

− 1

106 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

Интеграл вычисляется разложением в ряд экспоненты:

I =

∞

− 1

∞

−x

(1 + e

−x

+ e

−2x

+ . . .)dx.

Вычисляя члены суммы, получим

I =

∞

n=1

∞

−nx

dx =

∞

n=1

∞

−u

du = 3!

∞

n=1

= 3!

В результате получаем закон Стефана-Больцмана:

= σT

= π

∞

dω, (4.57)

где постоянная Стефана-Больцмана определяется выражением

σ =

60c

¯h

Ее численное значение равно σ = 5.67 ∗ 10

−8

Вт/м

или в практических единицах

q = 5.67(T [K]/100)

Вт/м

. Найдем выражение для радиационного потока в общем слу-

чае. Из уравнения переноса излучения (4.54) интегрированием по угловым переменным

получаем выражение для дивергенции радиационного потока:

∇ · q

∞

dωκ

− I

)do.

Сюда входит интенсивность излучения I

, которую нужно найти из решения уравнения

переноса излучения для всех частот, температур и в зависимости от остальных пара-

метров. Выражение для радиационного потока или дивергенции радиационного потока

можно найти достаточно просто в двух предельных случаях: оптически тонкого κ

l ¿ 1

и оптически толстого κ

l À 1 газов.

4.5.3 Оптически тонкий газ (κ

¿ 1)

В этом случае, если на объем газа не падает внешнее излучение, охлаждение тела из-

лучением возникает из-за того, что каждый элементарный объем излучает энергию

= κ

, и это излучение практически беспрепятственно выходит из объема. В этом

случае дивергенция радиационного потока равна

∇ · q

∞

dωκ

do.

Умножая и деля правую часть на функцию распределения черного тела

∇ · q

= 4 π

∞

dω

∞

dω

∞

dω,

получаем формулу Планка:

∇ · q

= 4 κ

σT

, (4.58)

где введен средний коэффициент поглощения Планка:

∞

dω

∞

dω

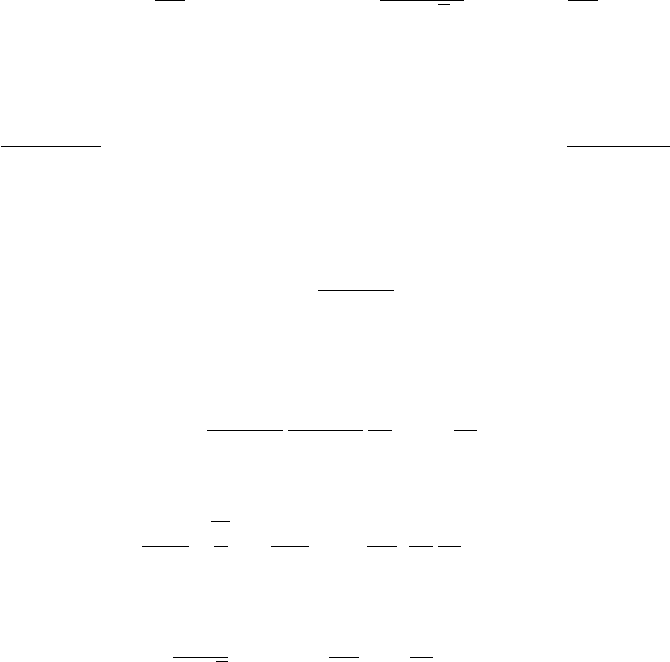
4.5. УРАВНЕНИЕ ПЕРЕНОСА ИЗЛУЧЕНИЯ 107

Это приближение описывает потери на излучение оптически тонкого нагретого тела,

поэтому оно называется также эмиссионным приближением. Коэффициент поглощения

Планка может быть вычислен в частных случаях. Для тормозного излучения на ионах

∞

min

−¯hω/kT

dω =

¯h

−¯hω

min

/kT

, κ

40 ∗ 2

7/2

√

αn

7/2

Рассчитаем коэффициент поглощения для фотоионизации, суммируя по всем уровням

ω,n

dω

(u)du, гдеu = ¯hω/kT, φ

(u) =

15u

− 1)

Формула для фотоионизации с уровня n с учетом индуцированного излучения имеет

следующую зависимость от частоты для идеальной плазмы:

ω,n

= C

1 − e

−u

Для неидеальной плазмы возникает сдвиг порога фотоионизации ¯hω = E

− E

+ ΓkT .

Интегрирование по частотам приводит к результату:

ω,n

= C

∞

1 − e

−u

− 1

du =

−u

Планковский коэффициент поглощения с уровня n имеет вид

32π

αf

¯hv

/kT

а суммарный планковский коэффициент поглощения

160

√

αn

max

n=1

/kT

где E

< 0. Отметим, что коэффициент поглощения Планка определяется областями

наибольшей непрозрачности внутри отличной от нуля области весовой функции Планка.

4.5.4 Оптически толстый газ (κ

l À 1)

В этом случае, если на некоторый объем газа падает излучение, оно поглощается и

становится изотропным, близким к излучению черного тела, поэтому внешнее излуче-

ние для оптически толстого тела несущественно. Отличие от излучения черного тела

определяется только неоднородностью распределения температуры. В этом случае ре-

шение уравнения переноса излучения можно найти, используя угловые моменты функ-

ции распределения фотонов, аналогичных решению задачи об электропроводности газа.

Определим моменты функции распределения:

fdo, (µ = cos ϑ, do = sin ϑdϑdφ).

Так

= 2 π

−1

fdµ

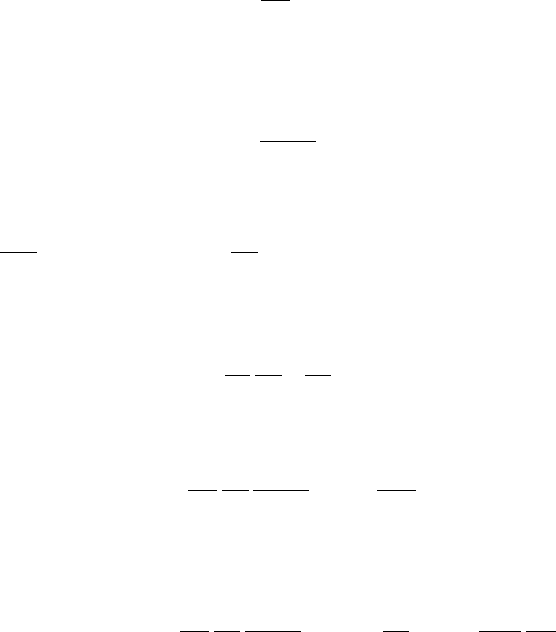
108 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

– величина, пропорциональная концентрации фотонов,

= 2 π

−1

fµdµ

– потоку фотонов, поскольку он определяется выражением

= j

(o)

vµfdo = vf

Рассмотрим поток импульса в направлении х:

fdo = pvf

следовательно, f

представляет поток импульса в направлении x, т.е. давление, произво-

димое диффундирующими частицами на поверхность, перпендикулярную x с точностью

до множителя pv. Для излучения pv = E. Высшие моменты функции распределения

определяют анизотропию светового давления. Решаем уравнение переноса излучения

(4.54) методом моментов. Умножим это уравнение на вектор n и проинтегрируем по

телесному углу, тогда получим

nn · ∇I

= −

do = −κ

Учитывая, что < nn >=

↔

/3, где

↔

– единичный тензор, получаем

= −

∇u

Здесь l

= 1/κ

– длина пробега фотонов с частотой ω. Используем связь спектральной

плотности энергии излучения с потоком излучения черного тела:

4πB

. (4.59)

Поясним выкладки, проведя их в координатной форме:

∂I

∂x

= κ

− I

∂

∂x

−1

do = −κ

µdo.

В левой части заменим I

на B

, что соответствует диффузионному приближению.

Тогда

(x)

= −

∂

∂x

4π

т.к.

−1

do =

−1

2πdµ = 4π /3 .

(x)

= −

∂

∂x

4πB

≡ D

∂u

∂x

где D

= l

c/3 – коэффициент диффузии фотонов. Радиационный поток вдоль направ-

ления x получаем, интегрируя по частотам:

∞

dω = −

∞

∂

∂x

4πB

dω = −

4π

∞

∂T

∂x

dω.

4.5. УРАВНЕНИЕ ПЕРЕНОСА ИЗЛУЧЕНИЯ 109

Отсюда следует, что радиационный поток тепла может быть представлен в виде закона

Фурье:

= −λ

∇T,

где λ

называется лучистой теплопроводностью:

4π

∞

dω =

4π

σT

Лучистая теплопроводность имеет вид

σT

. (4.60)

Деля и умножая на производную от функции распределения черного тела, получаем

∞

(dB

/dT )dω

∞

(dB

/dT )dω

Полученная средняя длина пробега излучения l

называется росселандовым средним

пробегом и определяется по формуле

∞

g(x)dx,

где весовая функция росселандова среднего

g(x) =

4π

−x

(1 − e

−x

)

, x = ¯hω/kT.

Средний росселандов пробег определяется областями малых значений коэффициентов

поглощения или больших пробегов фотона в области, где функция Планка отлична от

нуля.

4.5.5 Росселандов пробег для тормозных процессов

Росселандово среднее для тормозных процессов при рассеянии электронов на ионах

равно

αn

9/2

√

3π

8π

4π

∞

−x

(1 − e

−x

)

dx.

Интеграл вычисляется следующим образом:

∞

−x

(1 − e

−x

)

dx ≈

∞

−x

dx = 7! .

В результате получаем формулу для росселандова пробега:

10.89

. (4.61)

В общем случае росселандов пробег l

определяется областями малых значений коэффи-

циентов поглощения (больших пробегов) фотонов в области отличной от нуля функции

g(¯hω/kT )).

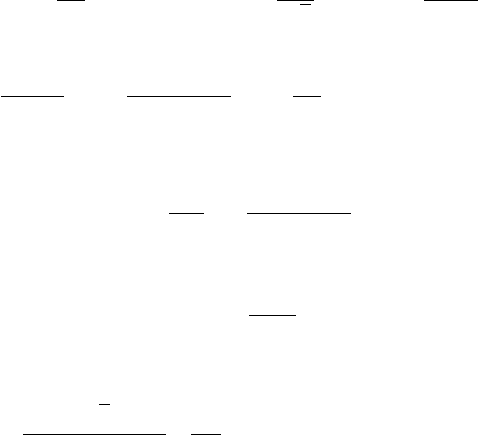
110 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

4.5.6 Росселандов пробег для фотоионизации

Вклад отдельного n-го пика фотоионизации является существенным в области ω

n+1

ω < ω

, где ¯hω

= −E

− ∆I, где ∆I = ΓkT – сдвиг порога фотоионизации

вследствие неидеальности, поэтому принимая частотную зависимость Крамерса для ко-

эффициента поглощения

ω,n

(1 − e

−u

), C

32π

√

αn

kT n

получаем

4π

n+1

exp −u

(1 − e

−u

)

du =

[F (u

) − F (u

n−1

)] ,

где u

= ¯hω

/kT , u

= ∞,

F (x) =

4π

−u

(1 − e

−u

)

du.

При x ¿ 1 функция

F (x) =

20π

В результате получаем, что роcселандово среднее для фотоионизации определяется по

формуле

√

32παn

max

n=0

[F (u

) − F (u

n−1

)]. (4.62)