Сон Э.Е. Лекции по физической механике

Подождите немного. Документ загружается.

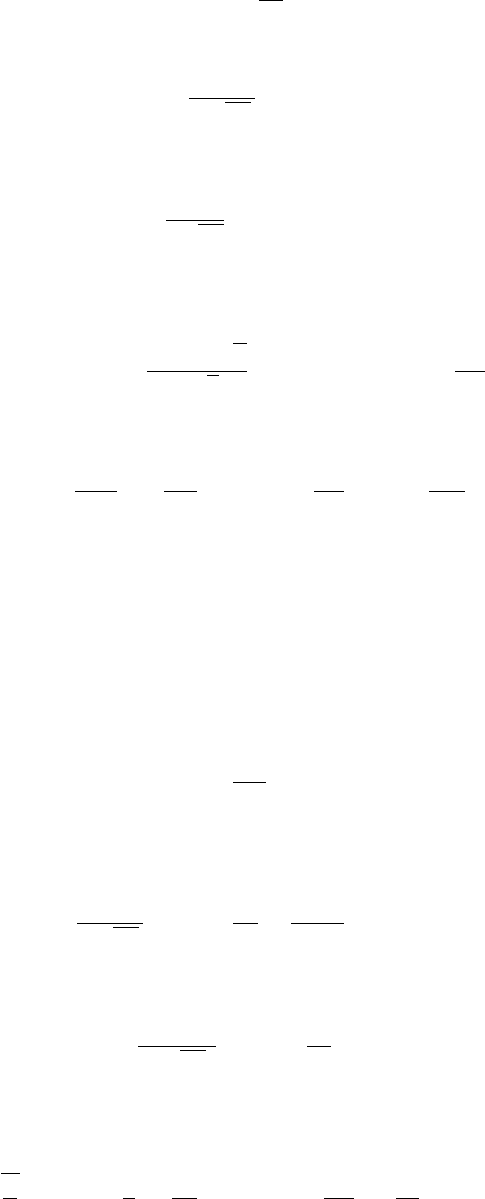
4.3. ФОТОРЕКОМБИНАЦИЯ 91

Суммирование по уровням Для суммирования по уровням воспользуемся формулой

для ζ-функции:

ζ(k) =

∞

n=1

с учетом которой

(rec)

∞

n=1

32αZ

√

3π

fIζ(3), (4.32)

где ζ(3) ≈ 1.2. Сравнивая с тормозным излучением:

(bs)

4αz

√

3π

приходим к объединению двух формул, учитывающее тормозные и фоторекомбинаци-

онные процессы:

4πε = 4π(ε

(bs)

+ ε

(rec)

) =

16αZ

√

fkT

1 + 2

ζ(3)

, (4.33)

или в практических единицах

4πε = 4.49

1/2

1 + 2

ζ(3)

Вт

см

Два члена в скобках определяют отношение вероятности фоторекомбинации к тормоз-

ному излучению. Вследствие большого отношения потенциала ионизации к температуре

вторая часть существенно больше, чем первая, следовательно при фоторекомбинации

энергии излучается больше, чем при тормозных процессах. Найдем коэффициент по-

глощения при фотоионизации. Для обратного процесса коэффициент поглощения для

фотоионизации с уровня n определяется формулой Крамерса. Используя связь меж-

ду прямым и обратным процессом, находим следующее выражение для коэффициента

поглощения:

ωn

Подставляя выражения для излучательной способности газа и спектральной плотности

излучения черного тела, получаем

ωn

32αZ

√

3π

kT n

−E

/kT

Коэффициент поглощения при тормозных процессах может быть записан в виде

8αZ

√

3π

Коэффициенты поглощения при тормозном поглощении излучения и поглощении при

фотоионизации с уровня n могут быть объединены в одну формулу:

= 2

αZ

πf

1 + 2

∞

−E

/kT

, (4.34)

92 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

где выражение в скобках также выражает соотношение между поглощением при тор-

мозном поглощении и при фотоионизации. Приближенное вычисление функции φ(I/kT )

(верхние уровни дают больший вклад) имеет следующий вид:

φ(I/kT ) = 2

∞

I/kT n

' 2

∞

I/kT n

dn,

полагая x = I/kT n

, x

= I/kT n

= ¯hω/kT , получаем

φ(I/kT ) =

dx = e

¯hω/kT

− 1.

Для тормозных и фотопроцессов

(bs,rec)

16π

αf

¯hω/kT

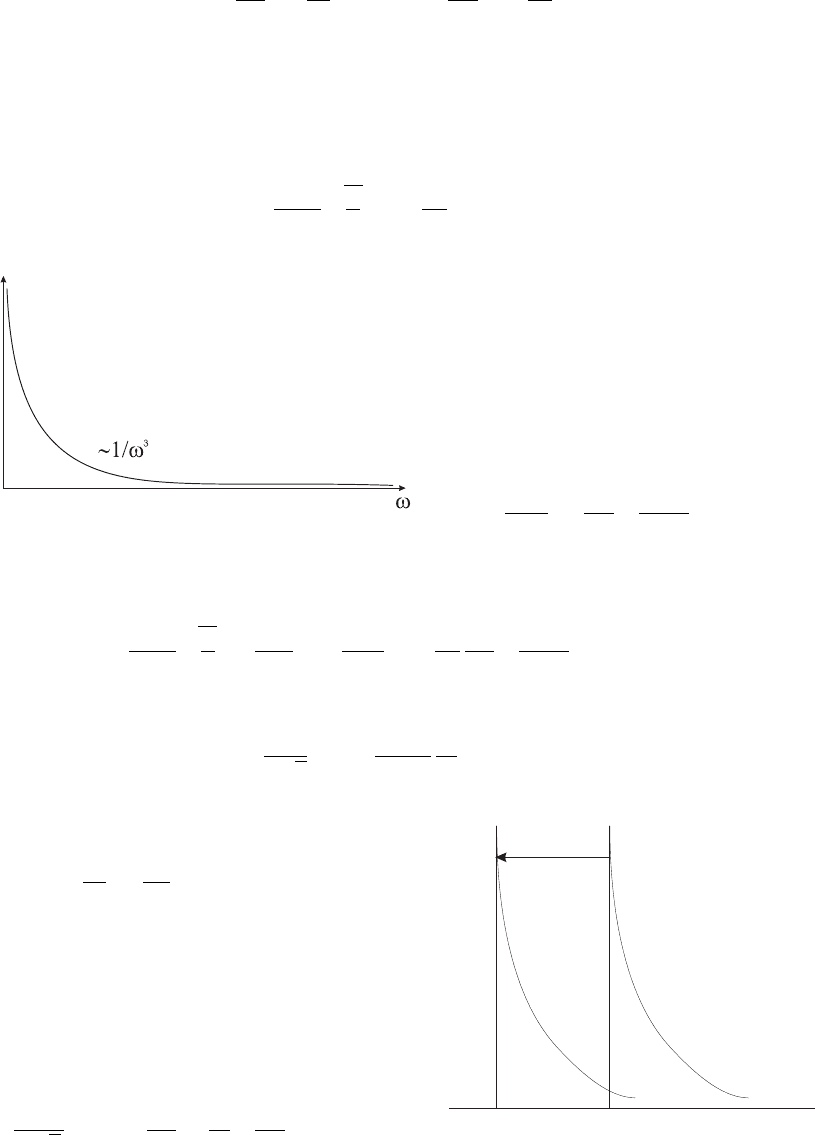
Рис. 4.5: Зависимость коэффициента поглощения от ча-

стоты для тормозных процессов

Отношение вклада фотопроцес-

сов и тормозных процессов равно

(exp ¯hω/kT − 1) : 1). Это соотноше-

ние много больше единицы для об-

ласти максимума функции Планка.

Коэффициент поглощения при фо-

тоионизации может быть преобразо-

ван с помощью формулы Саха:

mkT

2π¯h

3/2

−I/kT

Тогда получаем следующее соотно-

шение:

(bs,rec)

16π

2kT

3/2

mkT

2π¯h

3/2

−(I−¯hω)/kT

или после преобразований получаем

(bs,rec)

32π

√

αZ

(¯hω)

−(I−¯hω)/kT

Рис. 4.6: Сдвиг порога фотоионизации

Распределение атомов по уровням опреде-

ляется распределением Больцмана

= g

−(E

−E

)/kT

где E

= −I. Для атома водорода Z

4Ry

= 4(Ze

)

= 4I

, с учетом этих

формул суммируя выражения для тормозных

и фотоионизационных процессов, получаем ко-

эффициент поглощения окончательно в следу-

ющем виде:

(bs,rec)

128α

√

πa

¯hω

−(I−¯hω)/kT

(4.35)

4.4. ИЗЛУЧЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ В ПЛАЗМЕ 93

-1

-2

-3

-( - )w w

-3

hn = -e

2 2

hn = -e

1 1

Рис. 4.7: Коэффициент поглощения для фотоионизации с различных атомных уровней

Зависимость коэффициента поглощения от частоты приведена на рис. 4.7.

В плазме, вследствие взаимодействия или неидеальности, происходит сдвиг порога

фотоионизации в красную сторону, что показано на рис.4.6. Сдвиг порога фотоиони-

зации может быть оценен по разным формулам, соответствующим разным формулам

снижения потенциала ионизации. В частности, для дебаевского снижения потенциала

ионизации он имеет вид ¯hδω = ΓkT , где Γ – параметр неидеальности плазмы.

4.4 Излучение спектральных линий в плазме

Рассмотрим два атомных состояния 1 и 2, которые имеют энергии E

и E

и, соот-

ветственно, статистические веса g

и g

. Пусть заселенность первого уровня составляет

= n

V , а второго уровня – N

= n

V (см. рис. 4.8).

E ,g

2 2 2

,n

E ,g

1 1

,n

Рис. 4.8: Излучение спектральной линии

Разность энергий между этими

уровнями равняется кванту излуче-

ния E

− E

= ¯hω. Между этими

состояниями происходят спонтанные

переходы с вероятностью A

из 2 в 1

и индуцированные переходы с веро-

ятностями B

из 1 в 2 и B

из 2 в 1.

Для нахождения вероятностей пере-

ходов используем принцип соответ-

ствия Бора-Зоммерфельда, в кото-

ром фурье-компоненты |a

долж-

ны быть заменены в квантовом слу-

чае на матричные элементы перехо-

да из начального в конечное состояние | < m|a|n > |

. Интенсивность излучения в

классической теории поля определяется формулой

4ω

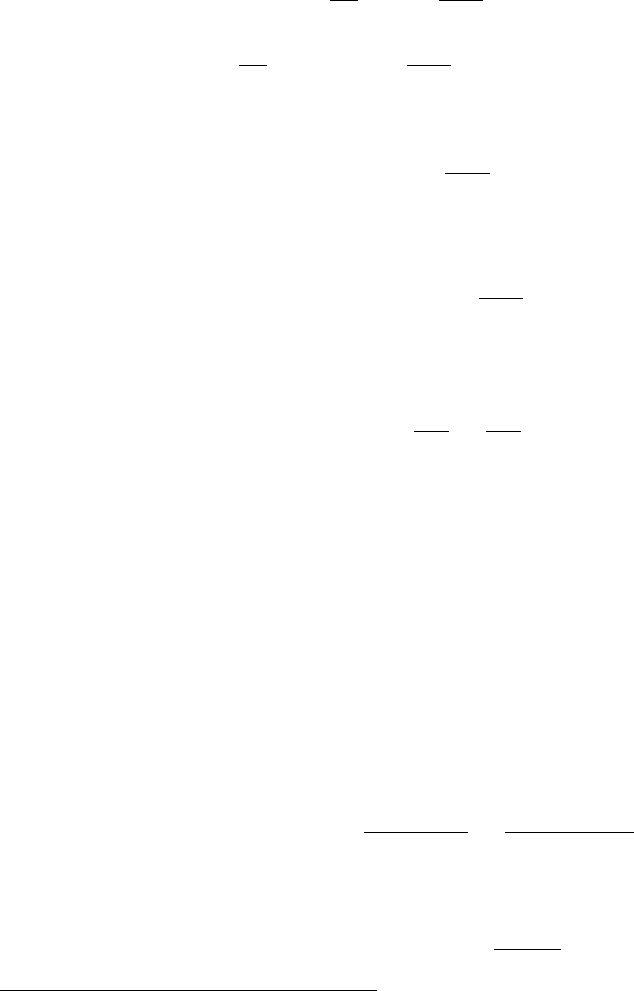
94 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

а полная излученная энергия

∆E =

∞

dω.

В квантовой электродинамике необходимо заменить |d

на | < 1|d|2 > |

= |d

, т.е.

фурье-компоненту дипольного момента на матричный элемент перехода для дипольного

момента. Затем необходимо просуммировать по конечным состояниям и для переходов,

происходящих под действием излучения и умножить на число фотонов в единице фа-

зового пространства. Тогда получаем вероятности переходов между состояниями 1 и

¯hω

4ω

3¯hc

≡ B

¯hω

(1 + f

4ω

3¯hc

(1 + f

≡ B

+ A

Этими соотношениями определяются коэффициенты Эйнштейна:

4ω

3¯hc

– вероятность индуцированного возбуждения равная числу переходов в единицу време-

ни,

= B

4ω

3¯hc

– вероятность спонтанного и индуцированного излучений. Отсюда следует соотношение

между вероятностями прямых и обратных индуцированных переходов:

. (4.36)

4.4.1 Сечения излучения и поглощения света в дискретном спектре

Введем плотность вероятности a

того, что атомная система может излучить квант в

интервале от ω до ω + dω. Эта вероятность имеет нормировку на 1, т.е. интеграл

∞

−∞

dω = 1.

Следовательно, a

представляет распределение фотонов по частотам, a

dω – вероят-

ность того, что атомная система может излучить частоту от ω до ω + dω. Сечение про-

цесса определяется как отношение вероятности перехода к потоку фотонов.

Сечение

перехода σ

определяется отношением вероятности процесса к потоку фотонов:

dω)

dω

dω)B

dω

где число фотонов в единице объема в интервале частот ω, ω + dω равно

dω = 2f

(2π¯h)

Выражение для A

отличается от принятых в другой литературе на множитель u

, где u

и f

– спектральная

плотность и функция распределения фотонов.

4.4. ИЗЛУЧЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ В ПЛАЗМЕ 95

где p

= ¯hω/c – импульс фотона с энергией ¯hω,

dω = 2f

4π¯h

dω

8π

¯h

dω

Подставляя это выражение в сечение перехода, получим связь сечения с коэффициен-

тами Эйнштейна:

dωB

dω

или σ

, (4.37)

где λ = 2πс/ω – длина волны излучения. Аналогично

. (4.38)

Подставляя выражения для коэффициентов Эйнштейна, получим сечения излучения и

поглощения света в дискретном спектре, которые выражаются через матричные эле-

менты дипольного момента начального и конечного состояний

4π

3¯hc

, σ

4π

3¯hc

. (4.39)

Найдем функцию распределения фотонов по частотам f

. В состоянии термодинамиче-

ского равновесия количество переходов из состояния 1 в 2 равно количеству переходов

из состояния 2 в 1:

= N

, или N

= N

(1 + f

откуда может быть найдена функция распределения фотонов по частотам f

. Отметим,

что мы здесь воспользовались принципом детального равновесия при известных вероят-

ностях прямых и обратных переходов для нахождения функции распределения фотонов

по частотам.

Коэффициенты Эйнштейна не зависят от состояния среды, поэтому рассмотрим слу-

чай термодинамически равновесной среды, когда концентраций состояний во 2 и в 1

состоянии определяются распределением Больцмана:

−¯hω/kT

Используя связь между вероятностями переходов прямого и обратного процессов, по-

лучаем выражение для функции распределения фотонов:

¯hω/kT

− 1

. (4.40)

Отметим, что сечение можно выразить через силу осциллятора, которая определяется

соотношением

2mω

¯he

так что

2π

3mc

Подставляя выражение для f

в интенсивность излучения черного тела, получаем фор-

мулу Планка.

96 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

4.4.2 Формы спектральных линий

Форма спектральной линии представляется функцией a

. Для атома в вакууме переход

происходит только в случае, когда разность энергий в точности равна разности энергий,

т.е.

= δ(¯hω − (E

− E

)).

На самом деле вследствие различных процессов δ-функция переходит в функцию конеч-

ной ширины, т.е. линии уширяются. Рассмотрим различные механизмы уширения спек-

тральных линий. Если возможны два механизма уширений, которые сравнимы между

собой, то результирующее уширение является сверткой

= a

(1)

∗ a

(2)

или

a(ω) =

(ω

− ω)dω

Так, например, возможны лоренцевский или гауссовский контуры (см. ниже). Свертка

этих контуров называется фойгтовской формой линии. Рассмотрим форму спектраль-

ной линии, определяемую различными механизмами.

4.4.3 Естественная ширина линии

С классической точки зрения атом, имеющий энергию E

, характеризуется гармони-

ческим осциллятором с частотой ω

и энергией E

= mω

/2. При излучении атом

теряет энергию, определяемую интенсивностью излучения. В дипольном приближении

уменьшение энергии осциллятора определяется по формуле

= −

Определим постоянную затухания отношением потери энергии в единицу времени к

энергии:

γ = −

3mc

Отношение постоянной затухания к частоте колебаний

2ω

пропорционально α

∝ 10

−7

, где α - постоянная тонкой структуры. Это означает, что

затухание является малым по сравнению с излучаемой частотой. В квантовой механике

возбужденное состояние является неустойчивым и переходит в основное состояние с

излучением кванта с вероятностью A

, т.е. возникает уширение спектральной линии

∆E ∝ ¯h∆ω ∝ ¯h/τ ∝ A

, откуда следует, что ∆ω ' A

. C учетом выражения для

коэффициента Эйнштейна получаем

∆ω

∝

¯hc

∝

∝ 10

−7

По этой причине естественная ширина линии крайне мала. Оценку ширины линии проще

всего произвести в атомной системе единиц (e = m = ¯h = 1). При этом единицей

4.4. ИЗЛУЧЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ В ПЛАЗМЕ 97

длины является первый боровский радиус, единицей скорости – скорость электрона на

первой боровской орбите, а единицей энергии – удвоенный потенциал ионизации атома

водорода. Из выражения для постоянной тонкой структуры α = e

/¯hc = 1/137 следует,

что в атомной системе единиц с = 137, т.е. скорость электрона на первой боровской

орбите в 137 раз меньше скорости света. Отношение полуширины линии к длине волны

составляет величину порядка 1/c

в атомных единицах, что соответствует значению

3 ∗ 10

−7

4.4.4 Доплеровская ширина линии

Источник, движущийся вдоль оси x и излучающий собственную частоту ω для сторонне-

го наблюдателя, находящегося в лабораторной системе координат, вследствие эффекта

Доплера кажется излучающим частоту, сдвинутую на ∆ω = ω

/c, где v

– продоль-

ная скорость, c – скорость света. Вследствие малой естественной ширины линии, можно

считать, что неподвижный атом излучает бесконечно узкую спектральную линию, для

которой функция распределения

= δ(ω − ω

)

удовлетворяет условию нормировки

∞

−∞

dω = 1. Интенсивность излучения характе-

ризуется усредненной по максвелловскому распределению формой линии:

< a

∞

−∞

δ(ω − ω

− ∆ω)

2πkT

3/2

−M(v

)/2kT

2πkT

1/2

∞

−∞

(ω − ω

1 +

¶¸

−Mv

/2kT

2πkT

1/2

−Mc

/2kT

− 1

Здесь использованы свойства δ-функции:

∞

−∞

δ(k(x − x

))f(x)dx = f(x

)/k.

Учитывая нормировку формы линии и вводя переменную ∆ω = ω − ω

вместо ω, нахо-

дим, что форма линии определяется функцией

a(∆ω)d∆ω =

d∆ω

2πkT

1/2

exp

"Ã

−

2kT

∆ω

Эта форма линии является гауссовской с полушириной, определяемой из равенства

exp





−Mc

2kT

!Ã

∆ω

1/2





откуда следует

∆ω

1/2

= ω

2kT

ln 2, или

∆ω

1/2

√

ln 2.

4.4.5 Штарковское уширение спектральных линий

98 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

)(

¥E

)(

¥E

1’

2’

Рис. 4.9: Излучение спектральной линии при движении

излучающего атома в электрическом поле заряженных

частиц

Спектральная линия возникает в

результате перехода между двумя

энергетическими уровнями с энерги-

ями E

и E

и с частотами ω

, ω

Величины E

и E

зависят от воз-

мущений, вызываемых присутству-

ющими атомами и молекулами, по-

этому E

= E

(r) и E

(r) (см.

рис. 4.9) являются функциями ко-

ординат, где r – расстояние меж-

ду излучающим атомом и частицей,

вызывающей возмущение. При хао-

тическом возмущении это приводит

к уширению линии. Возможны два

предельных случая для соотношения между ∆ω – сдвигом частоты возмущенного зна-

чения и v/ρ, где v – скорость, ρ – прицельный параметр. Отношение ρ/v ≈ τ – время

движения частицы в поле потенциала взаимодействия излучающего атома и воздей-

ствующей частицы. Возможны два предельных случая: при ωτ ¿ 1 фаза колебаний

меняется незначительно. Этот предельный случай описывается статистической теори-

ей. Другой предельный случай ωτ À 1 описывается ударной теорией. В этом случае за

малое изменение времени происходит быстрое изменение фазы. Эти два случая явля-

ются предельными по отношению к общему случаю с изменением фазы на величину,

определяемую формулой:

∆ϕ =

∆ωdt =

¯h

(r) − E

(r)] dt, гдеr = r(t).

4.4.6 Ударная теория

Естественная ширина линии возникает вследствие конечного времени жизни атома в

верхнем состоянии. Если удар возмущающей частицы происходит за время, меньшее

времени жизни, то происходит увеличение ширины, излучаемой линией. Предположим,

что атом излучает частоту ω в момент времени t от 0 до T , тогда фурье-амплитуда

электрического поля излучения определяется выражением

(T ) ∼

i(ω

−ω)t

dt =

i(ω

−ω)T

− 1

i(ω

− ω)

При единичном акте излучения распределение интенсивности по частотам определяется

квадратом поля, поэтому I∼ |E(ω, T )|

. Наблюдаемая линия, однако, является результа-

том излучения от многих атомов, излучающих в разные моменты времени, но в среднем

оно происходит в момент времени τ ∼ ν

−1

, где ν = nσ

v – частота столкновений. Веро-

ятность того, что данный атом излучает в течение времени T , равна τ

−1

−T/τ

, поэтому

функция ширины определяется выражением

=< |E

(T )|

или с учетом усреднения по столкновениям

= τ

−1

∞

(T )|

−T/τ

dT =

(ω

− ω)

+ ν

4.4. ИЗЛУЧЕНИЕ СПЕКТРАЛЬНЫХ ЛИНИЙ В ПЛАЗМЕ 99

Постоянную C найдем из условия нормировки

∞

−∞

dω = 1,

откуда следует C = ν

/π. В результате получаем, что для механизма ударного ушире-

ния контур линии является лоренцевским:

π[(ω − ω

)

+ ν

]

(4.41)

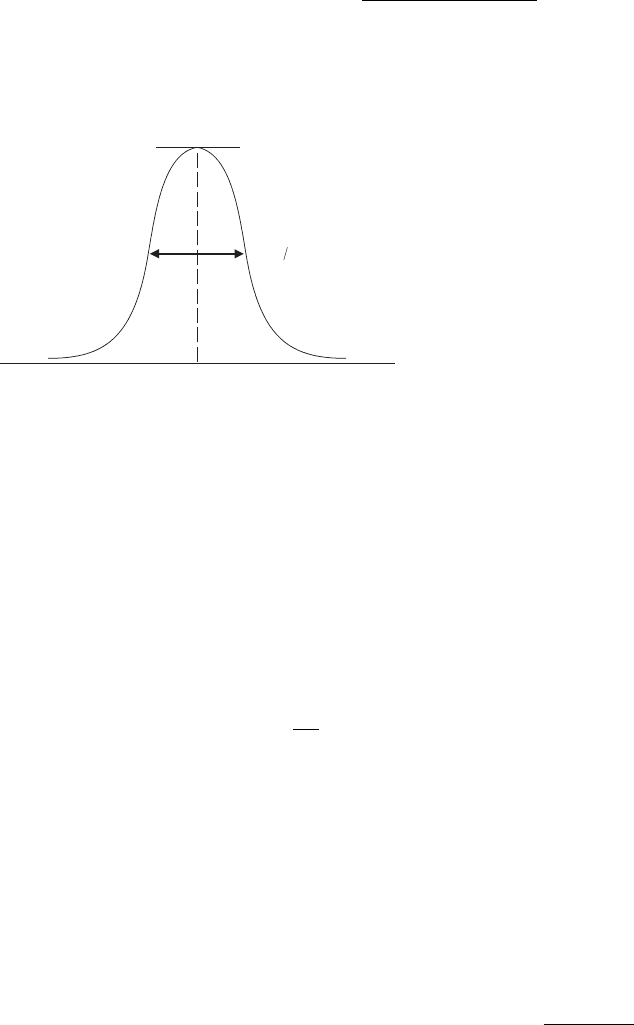
он представлен на рис. 4.10. Полуширина распределения определяется из условия a

(∆

) =

1/2, откуда следует ∆ω

1/2

= ν

1/2

Рис. 4.10: Полуширина спектральной линии

Скорость электронов много больше

скорости тяжелых частиц, поэтому удар-

ное уширение наиболее эффективно для

столкновений излучающих атомов с элек-

тронами. Здесь изложен простейший ва-

риант ударной теории. В действительно-

сти следует учитывать, что столкновения

вызывают эффекты двух типов:

• при столкновении может происхо-

дить тушение верхнего уровня, т.е.

имеет место кинетический процесс,

связанный с населенностью верхнего

уровня;

• сбой фазы излучающего состояния мо-

жет делить волновой пакет на две неко-

герентные части.

Статистическая теория При ωτ ¿ 1 при сближении частиц происходит малое измене-

ние частоты излучения, которое является функцией взаимного расположения частиц.

Поэтому

dω =

4π

. . .

. . . r

. . . dr

В этом уравнении область интегрирования ограничена той частью конфигурационного

пространства, где частота равна ω:

ω − dω ≤ ω(r

, . . . , r

) ≤ ω + dω.

В статистической теории обычно предполагается, что ω(r

, . . . , r

) =

ω(r

), что спра-

ведливо для больших значений r и несправедливо для малых, где вклады расположе-

ния отдельных частиц неаддитивны. Для описания воздействия возмущающих частиц

можно применять классическую или квантовую механику. Рассмотрим условия приме-

нения классической механики для описания траекторий частиц, в которой расстояние

между частицами определяется по формуле: r(t) =

√

+ v

. В квантовой механике

квантуется величина углового момента mvr ≈ l¯h. С учетом принципа неопределенности

m∆r∆v = ¯h получаем: (∆r/r)(∆v/v) = 1/l ¿ 1. При больших орбитальных моментах l,

100 ГЛАВА 4. ОПТИЧЕСКИЕ СВОЙСТВА ГАЗОВ

например, при l = 100, ∆r/r ≈ ∆v/v ∼ 0.1, т.е. столкновения с большими значениями

угловых моментов могут описываться классически. Теория Хольцмарка учитывает вли-

яние электрических микрополей на интенсивность излучения линии. Особенно хорошо

эта теория описывает крылья линий. В теории Хольцмарка учитываются только близ-

кие столкновения между излучающим атомом и ионом, вызывающим эффект Штарка.

Статистическое описание определяется большим числом столкновений ионов с атомом,

поэтому центр линии описывается хуже, чем крылья. Среднее электрическое поле в

плазме можно оценить с помощью среднего расстояния между частицами 4/3πr

n = 1,

= Ze

. Расположим излучающий атом в начале координат и опишем сферу ради-

усом r вокруг него. Обозначим P (r) – вероятность того, что по крайней мере один ион

находится внутри этой сферы. Для нахождения этой вероятности вычислим вначале

−

(r) = 1 − P (r), где P

−

(r) – вероятность того, что внутри сферы радиусом r нет ни

одного иона. По формуле умножения вероятностей можно записать:

−

(r + dr) = P

−

(r)p

−

где p

−

– вероятность того, что между r и r +dr нет ни одного иона. Эта величина может

быть вычислена разложением в ряд:

−

= 1 − 4πnr

dr − (4πnr

dr)

− . . . ,

где соответствующее величины выражают вероятность нахождения одной, двух и трех

частиц в элементе 4πr

dr. Ограничиваясь первым членом разложения и подставляя в

уравнение, получим

−

(r) + P

−

(r)dr = P

−

(r)(1 − 4πnr

dr).

Интегрируя это уравнение, получаем

−

(r) = Ce

−4πnr

По определению P

−

(0) = 1, поэтому C = 1 и окончательно находим вероятность нахож-

дения частиц внутри сферы радиусом r от излучающего атома:

P (r) = 1 − e

−4πnr

. (4.42)

Вероятность того, что элементарный шаровой слой содержит хотя бы один ион, опреде-

ляется дифференциалом этого уравнения:

dP (r) = 4πnr

−4πnr

dr. (4.43)

Это распределение называется "распределением ближайшего соседа" , т.к. фактор 4πnr

выражает вероятность нахождения иона между r и r + dr, а экспонента определяет

условие того, что внутри сферы радиусом r нет ни одного иона. Условие нормировки

распределения вычисляется как предел при r = R → ∞:

dP (r) = 1 − e

−N

→ 1, N =

πnR

Определив среднее расстояние между частицами (4/3)πn = r

−3

, получим окончательное

"распределение ближайшего соседа" в дифференциальной форме:

dP (r) = e

−(r/r

)

. (4.44)