Сон Э.Е. Лекции по физической механике
Подождите немного. Документ загружается.


1 СПРАВОЧНЫЕ ФОРМУЛЫ 7
Диссоциация идеального газа Для химиче-
ской реакции диссоциации, т.е. молекула A
2
распа-
дается на атомы A: A
2
*
)
2A. Условие химического
равновесия имеет вид µ
A
2
= 2µ
A
1
или подставляя
сюда выражение для химических потенциалов мо-
лекул и атомов получаем
n
2
A
n
A
2
= e
−βε
D
g
0
A
2
λ
3
A
2
g
A
2
λ
6
A
.
Принимая за общий уровень отсчета энергии ε =
0 энергию атома, получаем статистическую сумму
атома:
g
0
A
≡ g
A
= g
A
0
+ g
A
1
e
−βε
1
+ . . . ≈ g
A
0
,
где приближенно можно ограничиться основным
состоянием атома, т.к. диссоциация обычно проис-
ходит при температурах много меньших, чем энер-
гия первого возбужденного уровня состояния ато-
ма, т.е. βε
1
À 1. Отношение де-бройлевских длин
волн атомов и молекул равно
λ
A
λ
A
2
=
r
m
A
2
m
A
=
√
2.
Статистическая сумма молекулы
g
A
2
= e
−βε
0
g
0
A
2
,
где основное состояние молекулы имеет отрица-
тельную энергию, равную энергии диссоциации
ε
0
= −ε
D
, поэтому
g
A
2
= e
βε
D
g
0
A
2
.
Подставляя эти данные в выражение для химиче-
ского равновесия, получаем уравнение равновесия
химической реакции
n
2
A
n
A
2
= 2
3/2
g
2
A
λ
3
A
g
A
2
e
−βε
D
= K
p
. (21)
Правая часть этого уравнения называется кон-
стантой равновесия реакции диссоциации. При
расчете статистической суммы молекулы следу-
ет учесть, что возбуждение электронных уровней
несущественно. Энергия молекулы для основного
электронного состояния рассчитывается по фор-
муле, учитывающей колебательные и вращатель-
ные уровни.
ε
v,J
= ¯hω(v +
1
2
)[1 − x(v +
1
2
)] + B
v
J(J + 1),
здесь ¯hω – колебательный квант, а x – постоянная
ангармонизма. В результате получаем следующее
выражение для статистической суммы молекулы:
g
0
A
2
=
X
v ,J
(2J + 1)e
−βε
v,J
≈
≈
1
σ
g
J
g
v
≈
1
σ
(
k
B
T
B
e
)
e
y
e
2y
− 1
,
где σ – число, которое характеризует симметрию
молекулы. Статистические веса состояний для ато-
мов и молекул рассчитываются по параметрам, ко-
торые можно найти в справочнике или рассчитать
по следующим формулам: для атомов, для неболь-
ших зарядовых чисел Z, примерно до урана, дей-
ствует правило сильной связи, т.е. полный орби-
тальный момент равен сумме орбитального и спи-
нового моментов, соответственно статистический
вес состояния равен 2J+1. Для молекул в основном
состоянии спектроскопическое обозначение имеет
вид: X
3
P
−
g
, где индекс "3" есть 2S + 1, статисти-
ческий вес состояния равен 2S + 1 для
P
- состо-
яний, т.е. для нулевой проекции на оси, соединяю-
щие атомы в молекуле и 2(2S + 1) для всех осталь-
ных состояний. Например, для иона кислорода O
2
состояние D
2
P
4
имеет статистический вес 4, а спи-
ны ядер при этом можно не учитывать. Если рас-
стояние между вращательными уровнями мало по
сравнению с температурой, что почти всегда спра-
ведливо для вращательных подуровней, статисти-
ческую сумму можно рассчитать по формуле
g
J
= kT/B.
Расчет степени диссоциации молекул Опре-
делим степень диссоциации молекул α как отноше-
ние количества распавшихся молекул к первона-
чальному количеству молекул, т.е. числу молекул
до распада, часть из которых распалась при хими-
ческой реакции. При диссоциации одна молекула
распадается на два атома, поэтому степень диссо-
циации рассчитывается по формуле:
α =
n
A
/2
n
A
/2 + n
A
2
=
n
A
n
A
+ 2n
A
2
.
Введем вместо концентрации молекул n
A
полную
концентрацию молекул n
0
, используя полное число
частиц
n
0
=
p
k
B
T
= n
A
+ n
A
2
,
и выразим концентрации n
A
и n
A
2
через степень
диссоциации α и n
0
:
n
A
2
=
1 − α
1 + α
n
0
, n
A
=
2α
1 + α
n
0
.
Подставляя эти выражения в уравнение диссоциа-
ции, получаем
α
2
1 − α
2
=
K
p
kT
4p
.
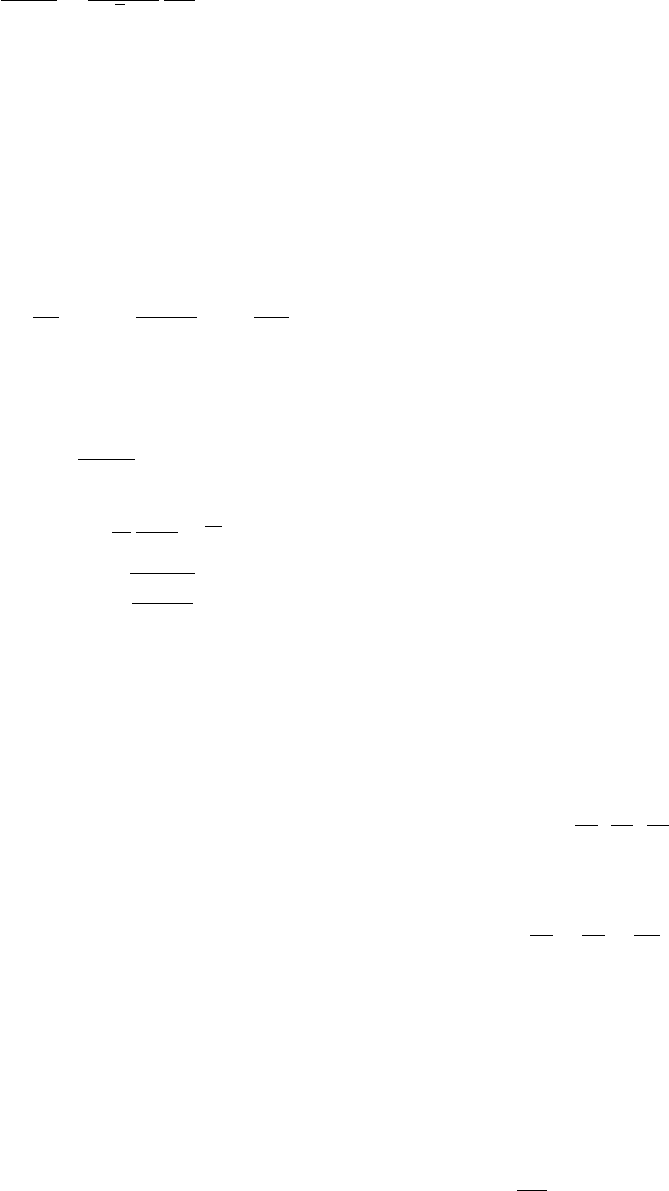
1 СПРАВОЧНЫЕ ФОРМУЛЫ 8
Подставляя константу химического равновесия,
получаем уравнение диссоциации
α
2
1 − α
2
=
kT
8
√
2pλ
3
A
g
2
A
g
0
A
2
e
−²
D
/kT
. (22)
В простейшем случае при расчете статистиче-
ской суммы можно ограничиться первым элек-
тронным уровнем, проинтегрировать по враща-
тельным уровням и использовать приближение
гармонического осциллятора для колебательных
уровней:
g
0
A
2
= g
R
A
2
g
V
A
2
g
E
A
2
,
где вращательная и колебательная статистические
суммы молекулы равны
g
R
A
2
=
kT
B
e
, g
V
A
2
=
e
y
e
2y
− 1
, y =
¯hω
2kT
.
Расчет степени ионизации атомов Констан-
та равновесия определяется по формуле:
α
2
1 − α
2
= K
p
,
K
p
= 21, 1
g
i
g
0
a
T
5/2
kK
P
atm
e
−
I
kT
+Γ
,
α =
s
K
p
1 + K
p
.
1.3.4 Термодинамические процессы и цик-
лы
Из курса общей физики необходимо знать процес-
сы, изображать их на всех парах термодинамиче-
ских параметров (p, V ), (T, S), (p, ρ), (h, s)
1. изотермический,
2. изохорический,
3. изобарический,
4. адиабатический,
5. политропический.
Из курса общей физики также необходимо
знать циклы и изображать их в координатах (p, V ),
(T, S) и знать, где они используются
1. Карно,
2. Ренкина,
3. Брайтона.
1.3.5 Минимальная и максимальная работа
Для системы в термостате сохраняются темпера-
тура, давление и химический потенциал, поэтому
минимальная работа, производимая термостатом
над системой для перехода из состояния 1 в со-
стояние 2 равна
W
min
= ∆E −T
(e)
∆S +p
(e)
∆V −
X
µ
(e)
i
∆N
i
. (23)
Если система совершает работу, находясь во
внешней среде, то максимальная величина работы,
которую может совершить система равна
W
max
= −[∆E − T
(e)
∆S + p
(e)
∆V −
X
µ
(e)
i
∆N
i
].
(24)
Величина работы, совершаемая телом или над
телом во внешней среде определяется величиной,
называеой " эксергия"
Ex = E − T
(e)
S + p
(e)
V −
X
µ
(e)
i
N
i
W
min
= ∆Ex, W
max
= −∆Ex. (25)
1.4 Несжимаемые жидкость или газ
при M
2
¿ 1
Для течений жидкости или газа при малых числах
Маха (M < 0.3) плотность можно считать посто-
янной ρ = const, в этом случае уравнение непре-
рывности имеет вид
∇ · v = 0, (26)
где v(u, v, w) - вектор скорости, а вектор
∇
µ
∂
∂x
,
∂
∂y
,
∂
∂z
¶
.
В компонентах уравнение непрерывности имеет
вид
∂u
∂x
+
∂v
∂y
+
∂w
∂z
= 0, (27)
Для квазиодномерного течения газа в канале пе-
ременного сечения с площадью A(x) для несжи-
маемого течения уравнение непрерывности имеет
вид
u(x)A(x) = const. (28)
Для стационарного течения несжимаемой жидко-
сти имеет место интеграл Бернулли
ρu
2
2
+ p + ρgz = const. (29)

1 СПРАВОЧНЫЕ ФОРМУЛЫ 9
1.5 Газовая динамика (сжимаемый
газ)
1.5.1 Адиабатические течения газа
Скорость звука в среде (газ, жидкость, твердое те-
ло) определяется формулой
a
2
=
µ
∂p
∂ρ
¶
S
=
r
k
p
ρ
=
√
kRT (30)
Скорость звука в газе при нормальных условиях
(300 K)
a
возд
=
√
1.4 · 287 · 300 = 347 м/c.
Скорость звука в воде составляет около 1500 м/c.
Движение газа определяется числом Маха
M =
u
a
. (31)
При M < 1 течение является дозвуковым, при
M > 1 – сверхзвуковым.
В стационарном случае из уравнений движе-
ния и энергии для адиабатического течения следу-
ет уравнение Бернулли для сжимаемого газа или
сохранение " полной энтальпии"
h +
u
2
2
= h
0
. (32)
Энтальпия совершенного газа
h = c
p
T =
c
p
R
p
ρ
=
a
2
k − 1
. (33)
Подставляя в (32), получим
a
2
k − 1
+
u
2
2
=
a
2
0
k − 1
, (34)
или
a
2
k − 1
+
u
2
2
=
a
2
∗
k − 1
+
a
2
∗
2
=
k + 1
2(k − 1)
a
2
∗
. (35)
Скорости звука в критическом сечении и затормо-
женном состоянии связаны соотношением
a
∗
=
2
k + 1
a
0
= 0.833 a
0
при k=1.4. (36)
Из уравнения (35) следует
µ
a
a
0
¶
2
+
µ
u
u
max
¶
2
= 1, (37)
где максимальная скорость газа
u
max
= a
0
r
2
k − 1
. (38)
В газовой динамике кроме числа Маха M вво-
дится коэффициент скорости λ:
λ =
u
a
∗
, (39)
где a
∗
обозначена скорость звука в том сечении
одномерного течения, где скорость течения равна
скорости звука (M
∗
= λ
∗
= 1).
Связь между числом Маха и коэффициентом
скорости λ:
1
M
2
+
k − 1
2
=
k + 1
2λ
2
. (40)
Это соотношение можно переписать в виде
2
(k + 1)M
2
=
1
λ
2
−
1
γ
2
, (41)
где
γ
2
=
k + 1
k − 1
.
(42)
Для двухатомного газа и воздуха k = 1.4, γ
2
= 6.
Соотношение между числом Маха и коэффициен-
том скорости λ можно переписать в виде
λ
2
= γ
2
M
2
M
2
+ 2/(k − 1)
. (43)
Газодинамический напор может быть выра-
жен через давление и число Маха
ρu
2
2
= kp
µ
M
2
2
¶
, (44)
Число Маха можно выразить через давление
M
2
=
2
k − 1
"
µ
p
0
p
¶
k−1
k
− 1
#
, (45)
в результате газодинамический напор выражается
через отношение давлений
ρu
2
2
=
k
k − 1
p
"
µ
p
0
p
¶
k−1
k
− 1
#
. (46)
1.5.2 Газодинамические функции изэнтро-
пического потока
Для одномерного потока текущие значения пара-
метров можно относить к параметрам затормо-
женного потока (u = 0, p = p
0
, T = T
0
, ρ = ρ
0
,
a = a
0
) или к параметрам сечения, в котором до-
стигается скорость звука (u = a
∗
, p = p
∗
, T = T
∗
,
ρ = ρ
∗
, a = a
∗
).
T
0
T
= 1 +
u
2
2c
p
T
= 1 +
k − 1
2
M
2
. (47)
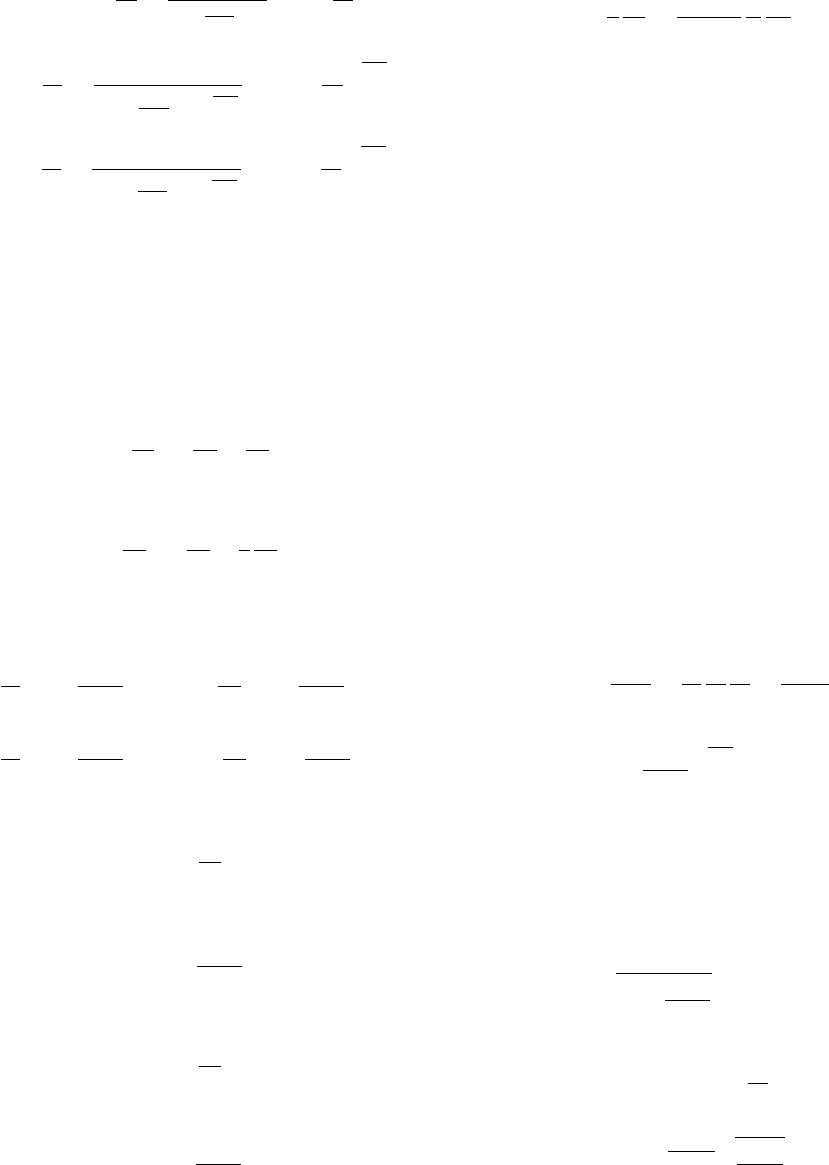
1 СПРАВОЧНЫЕ ФОРМУЛЫ 10
Газодинамические функции изэнтропического
потока определяются отношениями параметров в
данном сечении к параметрам торможения:
τ =
T
T
0
=
1
1 +
k−1
2
M
2
= 1 −
λ
2
γ
2
. (48)
π =
p
p
0
=
1
¡
1 +
k−1
2
M
2
¢
k
k−1
=
µ
1 −
λ
2
γ
2
¶
k
k−1
. (49)
ε =
ρ
ρ
0
=
1
¡
1 +
k−1
2
M
2
¢
1
k−1
=
µ
1 −
λ
2
γ
2
¶
1
k−1
. (50)
Сжимаемость газа определяется пара-
метром M
2
, поэтому при M
2
¿ 1 газ является
несжимаемым.
1.5.3 Простые волны Римана
Одномерные нестационарные течения сжимаемого
газа описываются уравнениями непрерывности
∂ρ
∂t
+ ρ
∂u
∂x
+
∂ρ
∂x
= 0 (51)
и движения (уравнения Эйлера)
∂u
∂t
+ u
∂u
∂x
+
1
ρ
∂p
∂x
= 0 (52)
Уравнение адиабаты 11связывает давление и плот-
ность Из уравнений (51) и (52) следуют уравнения
∂
∂t
µ
u ±
2a
k − 1
¶
+(u+a)
∂
∂x
µ
u +
2a
k − 1
¶
= 0, (53)
∂
∂t
µ
u −
2a
k − 1
¶
+ (u −a)
∂
∂x
µ
u −
2a
k − 1
¶
= 0 (54)
Вдоль характеристик
C
+
:
dx
dt
= u + a
сохраняются инварианты Римана
J
+
= u +
2a
k − 1
= const
i
, (55)
аналогично, вдоль
C
−
:
dx
dt
= u − a
сохраняются инварианты
J
−
= u −
2a
k − 1
= const
j
. (56)
1.5.4 Течения в каналах переменного сече-
ния
Ускорение потока в канале переменного сечения
1
u
du
dx
=
1
M
2
− 1
1
A
dA
dx
(57)
Из этого уравнения следует, что если канал
расширяется, то дозвуковой поток тормозится, та-
кое устройство называется дозвуковым диф-
фузором, а сверхзвуковой поток ускоряется, это
сверхзвуковое сопло. Для сужающегося кана-
ла дозвуковой поток разгоняется, такое устройство
называется дозвуковым соплом, а сверхзвуко-
вой поток тормозится, это сверхзвуковой диф-
фузор.
Для канала переменного сечения A(x) массо-
вый расход можно выразить через критические па-
раметры
ρ(x)u(x)A(x) = const = ρ
∗
a
∗
A
∗
≡ G. (58)
Уравнение движения для канала переменного се-
чения
£
p(x) + ρ(x)u
2
(x)
¤
A(x) = const =
= (p
∗
+ ρ
∗
a
2
∗
)A∗ ≡ J. (59)
Функция безразмерного расхода на единицу пло-
щади
q(λ) =
ρu
ρ
∗
a
∗
=
ρ
ρ
0
u
a
∗
ρ
0
ρ
∗
=
λε(λ)
ε(1)
=
=
µ
k + 1
2
¶
1
k−1
λε(λ). (60)
1.5.5 Форма сверхзвукового сопла
Массовый расход через сопло
G = ρuA = ρ
∗
a
∗
Aq(λ) =
= ρ
0
r
kRT
0
k + 1
2
Aq(λ) = const, (61)
ρ
∗
a
∗
= ρ
0
a
0
ε(1)
a
0
a
∗
=
= ρ
0
p
kRT
0
r
k + 1
2
.
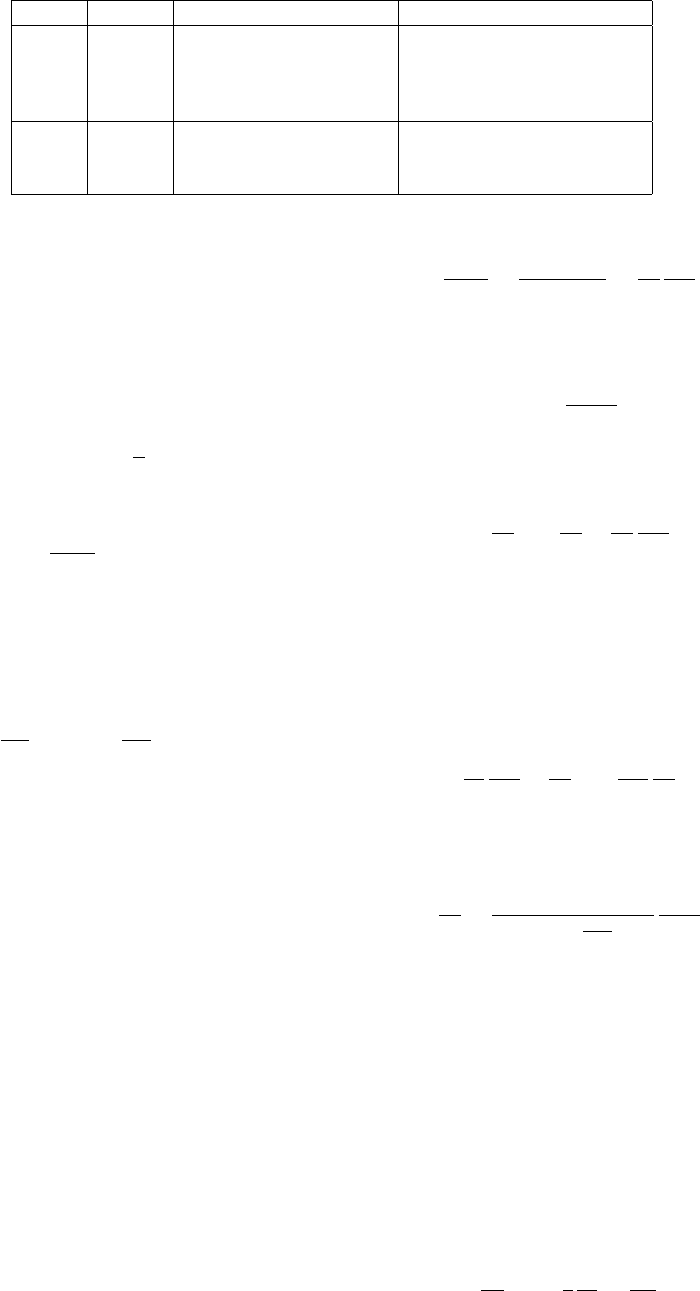
1 СПРАВОЧНЫЕ ФОРМУЛЫ 11
M < 1 M>1
поток торможение ускорение
→ du < 0 du > 0
dA > 0 dp > 0 dp < 0
дозвуковое сопло сверхзвуковой диффузор
поток dA > 0 du > 0 du < 0
→ dp < 0 dp > 0
дозвуковой диффузор сверхзвуковое сопло
1.5.6 Течения с теплоподводом
Из сохранения импульса и расхода через канал пе-
ременного сечения имеем:
J = (p + ρu
2
)A, G = ρuA.
Функция
z(λ) = λ +
1
λ
. (62)
Полный импульс газа в канале переменного сече-
ния
J =
k − 1
2k
Ga
∗
z(λ). (63)
Задача с подводом тепла к трубе с перемен-
ным сечением.
J
1
= J
2
, G
1
= G
2
,
отсюда следует
p
T
01
z(λ
1
) =
p
T
02
z(λ
2
),
λ
2
= f(λ
1
).
При решении уравнения для λ получается
квадратное уравнение, имеющее два решения. Фи-
зически правильным является решение λ < 1, т.к.
подогревом дозвукового потока через скорость зву-
ка перейти нельзя.
1.5.7 Сила тяги реактивного двигателя
Сила тяги реактивного двигателя определяется
равнодействующей сил, действующих на ракету.
Выражение для реактивной силы
R = G
возд
(u − U) + G
g
u + (p − p
a
)A. (64)
1.5.8 Течение сжимаемого газа с трением
на стенках канала
Сила трения на стенках для отрезка трубы диа-
метром D и длиной 4x
F = τ
w
πD4x.
F
A4x
=
τ
w
πD4x
4xπD
2
/4
=
4f
D
ρu
2
2
.
Коэффициент трения определяется отношени-
ем напряжения трения к газодинамическому напо-
ру потока
f =
τ
w
ρu
2
/2
(65)
Уравнение осредненного движения газа в трубе c
учетом трения о стенки канала
ρu
du
dx
= −
dp
dx
−
4f
D
ρu
2
2
. (66)
Для течения сжимаемого газа коэффициент тре-
ния является функцией числа Маха, числа Рей-
нольдса и качества канала (шероховатости стенок)
f = f(M, Re, ε).
Поделив на ρu
2
/2 уравнение (66), получим
1
u
2
du
2
dx
+
4f
D
= −
2
ρu
2
dp
dx
.
При известных значениях M и dM/dx коэффици-
ент трения может быть рассчитан по формуле
4f
D
=
1 − M
2
kM
4
¡
1 +
k−1
2
M
2
¢
dM
2
dx
. (67)
1.6 Динамика вязкой жидкости
1.6.1 Течение в трубе
При ламинарном движении жидкость в трубе дви-
жется под действием разности сил давления (на
выходе жидкости из трубы давление меньше, чем
на входе). Эта движущая сила уравновешена си-
лой трения жидкости о стенки трубы. В цилиндри-
ческих координатах (x, r, ϕ) градиент давления и
вектор скорости v = (U, 0, 0) направлены по оси x.
Уравнение движения выражает баланс сил и имеет
вид
−
∂p
∂x
= −µ
1
r
d
dr
µ
r
dU
dr
¶
. (68)
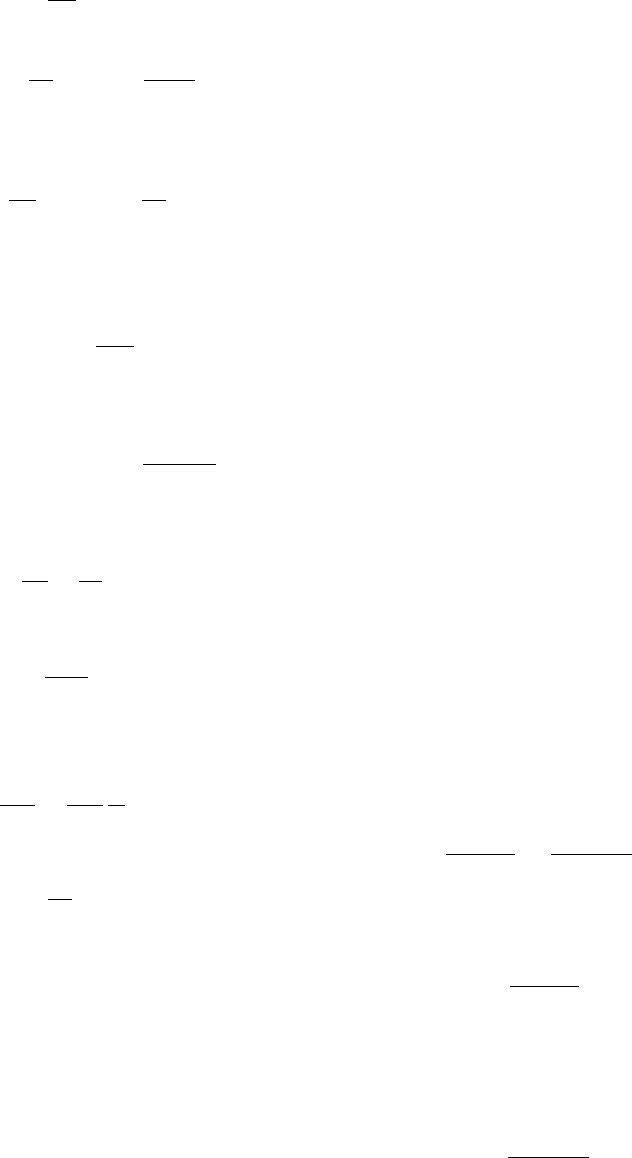
1 СПРАВОЧНЫЕ ФОРМУЛЫ 12
Решение уравнения движения с граничными
условиями прилипания и симметрии профиля ско-
ростей
U(R) = 0,
∂U
∂r
(0) = 0
имеет вид
U(r) = U
0
µ
1 −
r
2
R
2
¶
, U
0
=
R
2
∆p
4Lµ
.
Напряжение трения на стенке можно вычислить
двумя способами
τ
w
= −µ
µ
dU
dr
¶
r=R
= 4p
D
4L
,
или из баланса сил давления, действующих на пло-
щади входного и выходного сечений и трения на
поверхности трубы
τ
w
· πDL = 4p ·
πD
2
4
.
Расход жидкости определяется формулой
Пуазейля-Хагена
Q =
Z
ρUdA = 2πρ
Z
R
0
U(r)rdr =
π∆pρR
4
8Lµ
. (69)
Средняя скорость течения в трубе определяется
объемным расходом
¯
U =
Q
ρA
=
U
0
2
.
Число Рейнольдса для течения в трубе
Re =
ρ
¯
UD
µ
.
Коэффициент сопротивления трубы определяется
как отношение напряжения трения к динамическо-
му напору.
λ =
2τ
w
ρ
¯
U
2
=
2∆p
ρ
¯
U
2
D
L
(70)
Закон сопротивления трубы при ламинарном тече-
нии
λ =
64
Re
. (71)
На начальном участке трубы течение являет-
ся неустановившимся. По результатам эксперимен-
тальных и теоретических исследований длина на-
чального участка в ламинарном режиме определя-
ется числом Рейнольдса
l
in
= 0.03DRe
При критическом числе перехода от ламинарного
к турбулентному режиму (Re
cr
= 2300), длина на-
чального участка составляет l
in
= 69 D. При раз-
витой турбулентности длина начального участка
уменьшается и составляет l
in
= (25 − 40)D.
1.7 Критерии подобия, автомодель-
ность
Существует два способа получения критериев по-
добия. Первый основан на Π - теореме, в соответ-
ствии с которой вначале определяются возможные
размерные параметры, от которых может зависеть
решаемая задача (a, b, c, ...), затем предполагает-
ся, что существует безразмерная комбинация
Π = a
α
b
β
c
γ
, ...
C учетом размерности величин
a = M
a
M
L
a
L
T
a
T
, ...
получаем систему уравнений
a
M
α + b
M
β + c
M
γ + ... = 0,
a
L
α + b
L
β + c
L
γ + ... = 0,
a
T
α + b
T
β + c
T
γ + ... = 0.
Если эта система уравнений имеет решение
для α , β, γ, ..., то каждое решение дает безразмер-
ный параметр.
Другой способ получения безразмерных па-
раметров основан на уравнении, далее оценива-
ем члены и находим отношения членов уравнения,
что дает безразмерные параметры.
В гидро- и газовой динамике
1.8 Устойчивость течений
Неустойчивость Кельвина-Гельигольца
Неустойчивость Кельвина-Гельгольца для пло-
скопараллельного течения со скоростями U
1
, U
2
имеет фазовые скорости
c =
U
1
+ U
2
2
± i
|U
1
− U
2
|
2
, (72)
где вещественная часть фазовой скорости (c = c
0
+
ic
0
):
c
0
=
U
1
+ U
2
2
(73)
соответствует теореме Релея о том, что фазовая
скорость возмущений лежит в интервале между
максимальной и минимальной скоростями, а ин-
коремент неустойчивости Кельвина-Гельмгольца
γ = k
|U
1
− U
2
|
2
.

2 ЗАДАНИЕ 1. ТЕРМОДИНАМИКА И ТРАНСПОРТ 13
Неустойчивость Релея-Тейлора Рассматри-
вается неустойчивость двух слоев жидкости с
плотностями ρ
1
и ρ
1
в поле тяжести. Фазовая ско-
рость возмущений
c
2
= −
ρ
2
− ρ
1
ρ
2
+ ρ
1
g
k
(74)
Инкремент неустойчивости Релея-Тейлора
γ = c
0
k =
p
Agk, (75)
где число Атвуда
A =
ρ
2
− ρ
1
ρ
2
+ ρ
1
.
Неустойчивость Релея-Тейлора носит абсо-
лютный, а не конвективный характер.
1.9 Турбулентность
Турбулентное движение жидкости описывается
уравнениями для средних величин, совпадающи-
ми с ламинарным течением с добавлением турбу-
лентных напряжений Рейнольдса, так что общее
напряжение
σ
total
ij
= σ
Stokes
ij
+ σ
Reynolds
ij
,
где напряжения Рейнольдса для плоскопаралелль-
ного течения имеют вид
σ
R
xy
= µ
T
∂U
∂y
,
где U - продольная скорость, y поперечная к стенке
канала или трубы координата. Турбулентная вяз-
кость определяется формулой Прандтля
µ
T
= ρlw, w = l
∂U
∂y
где w - пульсационная скорость, l = κy - длина
смешения Прандтля, κ = 0.4 - постоянная Карма-
на.
Для слоя постоянного трения в канале или
трубе имеет место логарифмический профиль ско-
ростей (Задача).
1.10 Вязкопластические течения
Реологическое уравнение состояния для простого
случая бингамовсой среды приведено на рис. 1.
Движение жидкости в цилиндре представляет
недвижимую жидкость в центральной части, обте-
каемую вязкой жидкостью и внешнюю, Пуазелев-
скую.
Bingam (n=1)
Visco Plastic (n<1)
(Herschel - Buckley)
Dilatant (n>1)
Newton (n=1)
Pseudo plastic (n<1)
ε
τ
τ
0
S ~
dU
dr
0
Рис. 1: Реологическое уравнение состояния τ- S
для модели Бингама-Шведова
2 Задание 1. Термодинамика и
транспорт
2.1 Термодинамика газов и плазмы
1.1. Вычислить вращательную статистиче-
скую сумму при высоких температурах (kT > B
e
)
и удельную теплоемкость молекул N
2
, H
2
, O
2
.
Решение
Двухатомная молекула имеет вращательную
энергию E
I
= B
e
J(J + 1), где B
e
= ¯h
2
/2I,
I-момент инерции молекулы, вырождение уров-
ня g
J
= 2J + 1. Из таблицы для N
2
, H
2
, O
2
вращательные постоянные для них равны B
e
=
2 см
−1
; 60.85 см
−1
; 1.446 см
−1
.
Вращательная статистическая сумма
Z
rot
=
1
2
∞
X
0
(2J + 1) exp
·
−
J(J + 1)B
e
kT
¸
.
При B
e
/kT < 1 можно заменить суммирование по
J интегрированием:
Z
rot
=
Z
∞
0
e
−
J(J+1)B
e
kT
(2J + 1)dJ =
kT
B
e
,
Внутренняя энергия вращательных степеней сво-
боды
E
NkT
=
∂ ln Z
∂ ln T
,
E
rot
= NkT
2
∂ ln Z
rot
∂T
= NkT,
Теплоемкость вращательных степеней свободы
C
rot
= Nk = R
0
, E/N = kT.
1 см
−1
=1.44 К, поэтому при > 2.88 K, 87.6 K, 2.08
K для N
2
, H
2
, O
2
можно пользоваться классиче-
скими формулами.
2 ЗАДАНИЕ 1. ТЕРМОДИНАМИКА И ТРАНСПОРТ 14
Удельная вращательная теплоемкость газов
равна:
c
rot
N
2
=
Nk
µ
= R =
8314
2
= 296, 9
Дж
кг · K
,
c
rot
O
2
=
8314
32
= 259, 8
Дж
кг · K
,
c
rot
H
2
=
8314
2
= 4157
Дж
кг · K
.
Для учета поправок (B
e
/kT ¿ 1) используем
формулу Эйлера-Маклорена [Кубо]
∞
X
n=0
f(n) =
Z
∞
0
f(x)dx+
+
1
2
f(0) −
1
12
f
0
(0) +
1
720
f
000
(0) −
1
30240
f
4
(0) + . . . ,
где функция f(x) при при 0 < x < ∞
f(x) = (2x + 1)e
−x(x+1)σ
, σ =
B
e
kT
,
Z
∞
0
f(x)dx =
Z
∞
0
(2x+1)e
−x(x+1)σ
dx =
1
σ
Z
∞
0
e
−u
du =
kT
B
e
,
f(0) = 1, f
0
(0) = 2 −σ, f
00
= −12σ + 12σ
2
− σ
3
;
f
4
(0) = 120σ
2
− 10σ
3
+ 30σ
4
− σ
5
;
Z
rot
=
1
σ
+
1
3
+
σ
15
+
4σ2
315
+ O(σ
3
) =
=
kT
B
e
"
1 +
1
3
B
e
kT
+
1
15
µ
B
e
kT
¶
2
+
+
4
315
µ
B
e
kT
¶
3
+ O
µ
B
e
kT
¶
4
#
.
1.2. Двухатомная молекула может моделиро-
ваться гармоническим осциллятором с энергией
ε
n
= (
n
+ 1
/
2)¯
hω
и статистическим весом
g
n
= 1
.
Вычислить квантовую и классическую статистиче-
ские суммы осциллятора, внутреннюю энергию и
удельную теплоемкость для молекул O
2
, H
2
, при
температурах 300 К и 10000 К.
Решение
Из таблицы используем значения колебатель-
ных квантов молекул (¯hω
O
2
= 1580, см
−1
, ¯hω
H
2
=
4401см
−1
).
1)Статистическая сумма квантового осцилля-
тора равна
Z
v
=
∞
X
n=0
g
n
e
−βε
n
=
∞
X
n=0
e
−(n+
1
2
)¯hωβ
=
= e
β ¯hω
2
∞
X
n=0
e
−n¯hω
Z
v
=
e
−β¯hω/2
1 − e
−β¯hω
; ln Z
1
= −
β¯hω
2
− ln
¡
1 − e
−β¯hω
¢
,
где β = (kT )
−1
.
2) Для классического осциллятора:
Z
class
1
=
Z Z
∞
−∞
e
−βε(p,x)
dpdx
(2π¯h)
=
=
1
π¯h
Z
∞
−∞
e
−
βp
2
2m
dp
Z
∞
−∞
e
−
βmω
2
x
2
2
dx =
=
1
2π¯h
r
2πm
β
r
2π
β¯hω
=
1
β¯hω
.
Z
1
=
1
β¯hω
=
kT
¯hω
,
Z =
kT
Be
,
ln Z = ln T + C,
∂ ln Z
∂lnT
= 1.
3) Для системы N различающихся осциллято-
ров (см. лекции)
Z
N
= Z
N
1
=
µ
e
−β¯h
ω
2
1 − e
−β¯hω
¶
N
.
Внутренняя энергия равна
E
N
= −
∂ ln Z
∂β
= −
∂
∂β
N
·
−
β¯hω
2
− ln(1 − e
−β¯hω
)
¸
,
E
N
NkT
=
∂ ln Z
1
∂ ln T
= 1.
N¯hω
2
+
N¯hωe
−β¯hω
1 − e
−β¯hω
=
= N¯hω
µ
1
2
+
1
e
β¯hω
− 1
¶
.
c
v
=
∂E
N
∂T
= N¯hω
e
β¯hω
(e
β¯hω
− 1)
2
¯hω
kT
2
= Nk
y
2
e
y
(e
y
− 1)
2
,
y =
¯hω
kT
2 ЗАДАНИЕ 1. ТЕРМОДИНАМИКА И ТРАНСПОРТ 15
c
v
=
C
v
µ
=
Nk
µ
y
2
e
y
(e
y
− 1)
2
= R
y
2
e
y
(e
y
− 1)
2
.
Кислород:
T = 300 K
y =
¯hω
kT
=
1580 · 1, 44
300
= 7, 584,
R =
8314
32
= 259, 8
Дж
кг · K
,
c
vO
2
(300) = 259, 8 ·
7, 584
2
e
7,584
(e
7,584
− 1)
2
= 7, 607
Дж
кг · K
.
T = 1000K;
y =
¯hω
kT
=
1580 · 1, 44
1000
= 2, 28,
c
v O
2
(1000) = 259, 8 ·
2, 28
2
· e
2,28
(e
2,28
− 1)
2
= 171, 7
Дж
кг · K
.
Водород:
T = 300 K
R =
8314
2
= 4157
Дж
кг · K
, y =
¯hω
kT
=
4401 · 1, 44
300
= 21, 1,
c
vH
2
(300) = 4157
21, 1
2
· e
21,1
(e
21,1
− 1)
2
= 1, 24 · 10
−3
Дж
кг · K
,
T = 1000 K
c
vH
2
(1000) = 4157
6, 34
2
e
6,34
(e
6,34
− 1)
2
= 296
Дж
кг · K
y =
4401 · 1, 44
1000
= 6, 34.
1.3. Молекула кислорода имеет низколежащий
электронный уровень a
1
∆
g
, энергия которого ε
1
=
0, 982 эВ, а статистический вес g
1
= 2. Основное
состояние молекулы X
3
P
g
имеет статистический
вес g
0
= 3. Найти максимальное значение удельной
электронной теплоемкости кислорода и температу-
ру, при которой оно достигается (Б.М.Смирнов).
Решение
Статистическая сумма идеального газа с внут-
ренними степенями свободы определяется по фор-
муле
Z = Z
tr
(z
1
)
N
= e
−β(F
0
+∆F )
,
где
z
1
=
X
g
n
e
−βε
n
= g
0
e
−βε
0
+ g
1
e
−βε
1
=
= −g
0
e
−βε
0
¡
1 + ge
−β∆ε
¢
,
где g = g
1
/g
0
.
Электронная часть свободной энергии равна
β∆F
el
= −N ln e
−βε
0
(g
0
+ g
1
e
−β∆ε
) =
= Nβε
0
− N ln(g
0
+ g
1
e
−β∆ε
).
Внутренняя энергия определяется из свобод-
ной энергии
∆E
el
=
∂β∆F
∂β
= N
·
ε
0
+
g
1
∆εe
−β∆ε
g
0
+ g
1
e
−β∆ε
¸
=
= N
·
ε
0
+
∆εϕ
1 + gϕ
¸
,
где ϕ = e
−u
, u = ∆ε/kT .
Молярная теплоемкость равна
C
el
v
=
∂∆E
el
∂T
= N∆ε
µ
ϕ
1 + gϕ
¶
0
ϕ
e
∆ε/kT
∆ε
kT
2
,
Удельная теплоемкость
c
el
v
= R
(β∆ε)
2
e
−β∆ε
(1 + ge
−β∆ε
)
2
= Rf(β∆ε).
Найдем максимум функции
f(u) =
u
2
e
−u
(1 + ge
−u
)
2
=
u
2
e
u
(e
u
+ g)
2
,
f
0
(u) =
1
(e
u
+ g)
4
[(2ue
u
+ u
2
e
u
)(e
u
+ g)
2
−
−u
2
e
u
2(e
u
+ g)e
u
] = 0.
Получаем уравнение
(2 + u
0
)(e
u
0
+ g) = 2u
0
e
u
0
, или
u
0
= ln g + ln
u
0
+ 2
u
0
− 2
= ln g
(u
0
+ 2)
(u
0
− 2)
.
При g = 1 это уравнение имеет корень u
0
= 2, 40;
при g = g
1
/g
0
= 2/3 корень u
0
= 2, 29. Макси-
мальное значение функции при g = 2/3 равное
f(u
0
) = 0, 466 достигается при
T
max
=
∆ε
u
0
=
ε
1
u
0
=
0, 982 · 11605
2, 29
= 4976K.
Максимальное значение удельной теплоемкости
равно:
c
el
v
max
= Rf(u
0
) = (8314/32) ·0, 466 = 121, 1 Дж/кг
K.
Ответ: T
max
= 4976 K, c
el
v
max
= 121, 1 Дж/кг K.
2 ЗАДАНИЕ 1. ТЕРМОДИНАМИКА И ТРАНСПОРТ 16
1.4. Вычислить второй вириальный коэффи-
циент B
2
(T ) для газа с межмолекулярным потен-
циалом взаимодействия
a) Φ(r) =
(
∞ при r < r
0
−Φ
0
при r
0
< r < λr
0
0 при λr
0
> r
b) Φ(r) = Φ
0
³
r
0
r
´
n
и построить графики потенциалов и зависимости
B
2
(T ).
1.5. Вычислить второй вириальный коэффи-
циент B
2
(T ) для газа с межмолекулярным потен-
циалом взаимодействия
a) Φ( r) =
n
∞ при r < r
0
0 при r > r
0
b) Φ(r) =
∞ при r < r
0
Φ
0
·
λ
3
−
³
r
r
0
´
3
¸
при r
0
< r < λr
0
0 при r > r
0
и построить графики потенциалов и зависимости
B
2
(T ).
Решение
Для потенциала твердых сфер a)
B
2
(T ) =
Z
r
0
0
+
Z
∞
r
0
= 2π
Z
r
0
0
r
2
dr =
2
3
πr
3
0
.
b)B
2
(T ) =
Z
r
0
0
+
Z
λr
0
r
0
=
2
3
πr
3
0
−
2π
Z
λr
0
r
0
½
e
βΦ
0
£
(
r
r
0
)
3
−λ
3
¤
− 1
¾
r
2
dr =
=
2
3
πr
3
0
− 2πr
3
0
Z
λ
1
n
e
α(x
3
−λ
3
)
− 1
o
x
2
dx,
Z
λ
1
e
α(x
3
−λ
3
)
x
2
dx = e
−αλ
3
Z
λ
1
e
αx
3
x
2
dx =
=
1
3α
e
−αλ
3
e
αx
3
|
λ
1
=
e
−αλ
3
3α
¡
e
αλ
− e
α
¢
=
=
1
3α
h
1 − e
−α(λ
3
−1)
i
,
B
2
(T ) =
2
3
πr
3
0
−
−2πr
3
0
½
1
3α
h
1 − e
−α(λ
3
−1)
i
− (λ
3
− 1)
¾
=
=
2
3
πr
3
0
½
1 −
1
α
h
1 − e
−α(λ
3
−1)
i
+ λ
3
− 1
¾
,
B
2
(T ) =
2
3
πr
3
0
½
λ
3
−
1
βΦ
0
·
·
h
1 − e
−βΦ
0
(λ
3
−1)
io
.
Выражение для потенциала твердых сфер по-
лучается в следующих случаях:
1) λ = 1, 2) βΦ
0
→ 0, 3)Φ
0
→ ∞.
Точнее, рассмотрим потенциал
Φ(r) =
∞, при r < r
0
−
Φ
0
α
3
−1
·
α
3
−
³
r
r
0
´
3
¸
, при r
0
< r < αr
0
,
0 при r > αr
0
B
2
(T ) =
2
3
πr
3
0
"
α
3
−
µ
Φ
0
kT (α
3
− 1)
¶
−1
³
e
Φ
0
kT
− 1
´
#
;
Обозначим
B
2
(T )
2
3
πr
3
0
= b,
kT
Φ
0
= τ,
тогда в безразмерной форме второй вириальный
коэффициент
b = α
3
−
τ
α
3
− 1
³
e
1
τ
− 1
´
,
В пределе τ → ∞
b = α
3
−
τ
α
3
− 1
µ
1
τ
¶
=
(α
3
− 1)α
3
− 1
α
3
− 1
=
α
6
− α
3
− 1
α
3
− 1
.
1.6. Вычислить второй вириальный коэффи-
циент B
2
(T ) для газа с межмолекулярным потен-
циалом взаимодействия
a) Φ(r) =
(
∞ при r < r
0
−Φ
0
при r
0
< r < λr
0
0 при λr
0
> r
b) Φ(r) = Φ
0
³
r
0
r
´
n
и построить графики потенциалов и зависимости
B
2
(T ).
Решение
a)
B
2
(T ) =
Z
r
0
0
+
Z
λr
0
r
0
+
Z
∞
λr
0
=
=
2
3
πr
3
0
− 2π
Z
λr
0
r
0
¡
e
βΦ
0
− 1
¢
r
2
dr =
=
2
3
πr
3
0
−
2
3
πr
3
0
¡
e
βΦ
0
− 1
¢¡
λ
3
− 1
¢
